Основные свойства двойного интеграла. Задача двойной интеграл определение основные свойства двойного интеграла Двойной интеграл основные понятия и определения

Основные свойства двойного интеграла

Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.

1° . Аддитивность . Если функция f (x , y ) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D 1 и D 2 , то функция f (x , y ) интегрируема в каждой из областей D 1 и D 2 , причем

2° . Линейное свойство . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , а α и β - любые вещественные числа, то функция [α · f (x , y ) + β · g (x , y )] также интегрируема в области D , причем

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

6° . Теорема о среднем значении . Если обе функции f (x , y ) и g (x , y ) интегрируемы в области D , функция g (x , y ) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f (x , y ) в области D , то найдется число μ , удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

Задача, приводящая к понятию двойного интеграла Определение двойного интеграла Основные свойства двойного интеграла Площадь плоской области Сведение двойного интеграла к повторному Замена переменных в двойном интеграле Элемент площади в криволинейных координатах Якобиан и его геометрический смысл Формула замены переменных в двойном интеграле Двойной интеграл в полярных координатах

Задача, приводящая к понятию двойного интеграла. Определение двойного интеграла. К понятию двойного интеграла мы приходим, решая конкретную задачу вычисления объема цилиндрического тела. Цилиндрическим телом называется тело, ограниченное плоскостью хОу, некоторой поверхностью и цилиндрической поверхностью, образующие которой параллельны оси (см. рис.1). Область D изменения переменных х и у называется основанием цилиндрического тела. При определении объема тела будем исходить из двух принципов: !) если разбить тело на части, то его объем равен сумме объемов всех частей (свойство аддитивности); 2) объем прямого цилиндра, ограниченного плоскостью z = const, параллельной плоскости хОу, равен площади основания, умноженной на высоту. В дальнейшем мы будем предполагать, что область D является связной (состоящей из одного куска), квадрируемой (т. е. имеющей площадь) и ограниченной (т. е. расположенной внутри некоторого круга с центром в начале координат). Пусть - непрерывная функция точки Р(х, у) в области всюду в области Z>, т. е. что рассматриваемая цилиндрическая поверхность целиком лежит над плоскостью хОу. Обозначим объем цилиндрического тела через V. Разобьем область D - основание цилиндрического тела - на некоторое число п непересекающихся квадрируемых областей произвольной формы; будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, площади - через соответственно. Назовем диаметром частичной области Dk величину Задача, приводящая к понятию двойного интеграла Определение двойного интеграла Основные свойства двойного интеграла Площадь плоской области Сведение двойного интеграла к повторному Замена переменных в двойном интеграле Элемент площади в криволинейных координатах Якобиан и его геометрический смысл Формула замены переменных в двойном интеграле Двойной интеграл в полярных координатах где символ р{Р; Q) означает расстояние между точками Р и Q. Обозначим через d наибольший из диаметров частичных областей Dk (к = 1,2,..., п). Проведем через границу каждой частичной области цилиндрическую поверхность с образующими, параллельными оси Oz. В результате цилиндрическое тело окажется разбитым на п частичных цилиндричесжх тел. Заменим к-ое частичное тело прямым цилиндром с тем же основанием и высотой, равной аппликате какой-нибудь точки заменяемой поверхности (рис. 2). Объем такого цилиндра равен где точка - площадь области Dk. Проделав описанные построения для каждого частичного цилиндрического тела, получим п-ступенчатое тело, объем которого (о Интуитивно ясно, что Vn тем точнее выражает искомый объем V, чем меньше размеры частичных областей Dk. Принимаем объем V цилиндрического тела равным пределу, к которому стремится объем (1) п-ступенчатого тела при n-юои стремлении к нулю наибольшего диаметра d частичных областей Dk. Естественно, предел не должен зависеть от вида разбиения области D на частичные области Dk и от выбора точек Рк в частичных областях. Пусть /(х, у) - произвольная функция, заданная в области D. Сумма п (1) называется интегральной суммой для функции f(x}y) по области D, соответствующей данному разбиению этой области на п частичных областей и данному выбору точек Ж®*,!/*) на частичных областях Dk. Определение. Если при d -* О существует предел интегральных сумм п не зависящий ни от способа разбиения области D на частичные области, ни от выбора точек Рк в частичных областях, то он называется двойным интегралом от функции f(P) (или f(x, у)) по области D и обозначается символом ИЛИ Итак, (2) Самафункция f(x, у) при этом называется интегрируемой в области D (f(P) - подынтегральная функция, f(P) dS - подынтегральное выражение, dS - дифференциал (или элемент) площади, область D - область интегрирования; точка Р(®, у) - переменная тонка интегрирования). ,.. Возвращаясь к цилиндрическому телу, заключаем: объем цилиндрического тела, ограниченного плоскостью хОу, поверхностью, и цилиндрической поверхностью с образующими, параллельными оси Ог, равен двойному интегралу от функции /(х, у) по области D, являющейся основанием цилиндрического тела./ ИЛИ Здесь dx dy - элемент площади в декартовых координатах. Таков геометрический смысл двойного интеграла от неотрицательной функции. Если то объем Если в области D функции f(P) принимает как положительные, так и отрицательные значения, то интеграл представляет алгебраическую сумму объемов тех частей тела, которые расположены над плоскостью хОу (берутся со знаком «+»), и тех частей тела, которые расположены под плоскостью хОу (берутся со знаком «-»). К составлению сумм вида (1) для функции двух независимых переменных и к последующему предельному переходу приводят самые разнообразные задачи, а не только задача об объеме цилиндрического тела. Сформулируем достаточные условия интегрируемости. Теорема 1. Всякая функция у), непрерывная в ограниченной замкнутой области D, интегрируема в этой области. Требование непрерывности подынтегральной функции часто оказывается слишком стеснительным. Для приложений важна следующая теорема, гарантирующая существование двойного интеграла для некоторого класса разрывных функций. Будем говорить, что некоторое множество точек плоскости, имеет площадь нуль, если его можно заключить в многоугольную фигуру сколь угодно малой площади. Теорема 2. Если функция /(ж, у) ограничена в замкнутой ограниченной области D и непрерывна всюду в D, кроме некоторого множества точек площади нуль, то эта функция интегрируема в области D. §2. Основные свойства двойного интеграла Двойные интегралы обладают рядом свойств, аналогичных свойствам определенного интеграла для функций одной независимой переменной. 2.1. Линейное свойство Если функции) интегрируемы в области D, а а и р - любые вещественные числа, то функция af) также интегрируема в области D, причем о) 2.2. Интегрирование неравенств Если функции) интегрируемы в области D и всюду в этой области то (2) т. е. неравенства можно интегрировать. В частности, интегрируя очевидные неравенства получим Площадь плоской области Площадь плоской области D равна двойному интегралу по этой области от функции, тождественно равной единице. Действительно, интегральная сумма для функции /(Р) = 1 в области D имеет вид и при Любом разбиении области D на частичные области Dt, равна ее площади S. Но тогда и предел этой суммы, т. е. двойной интеграл, равен площади S области D: или, что то же, (3) 2.4. Оценка интеграла Пусть функция /(Р) непрерывна в ограниченной замкнутой области D, пусть М и тп - наибольшее и наименьшее значения /(Р) в области D и 5 - ее площадь. Тогда (4) 2.5. Аддитивность: Если функция /(Р) интегрируема в области D и область Z) разбита на две области D\ и Di без общих внутренних точек, то /(Р) интегрируема на каждой из областей D\ и Di, причем (5) 2.6. Теорема о среднем значении Теорема 3 (о среднем значении). Если функция /(Р) непрерывна в замкнутой ограниченной области D, то найдется по крайней мере одна точка Рс области D такая, что будет справедлива формула и где S - площадь области D В самом деле, так как /(Р) непрерывна в замкнутой ограниченной области D, то она принимает в D свое наибольшее значение М и свое наименьшее значение т. По свойству 4 об оценке интеграла имеем Таким образом, число заключено между наибольшим и наименьшим значениями функции /(Р) в области D. В силу непрерывности функции /(Р) в области D она принимает в некоторой точке Рс G D значение, равное этому числу, откуда S Значение f(Pc), определяемое поформуле (7), называется средним значением функции f(P) в области D. Геометрически й смысл теоремы о среднем значении Если в области D функция /(Р) ^ О, то формула (6) означает, что существует прямой цилиндр с основанием D (площадь которого равна 5) и высотой Н = /(Рс), объем которого равен объему цилиндрического тела (рис. 3). § 3. Сведение двойного интеграла к повторному Одним из эффективных способов вычисления двойного интеграла является сведение его к повторному. 3.1. Случай прямоугольника Пусть область D - замкнугый прямоугольник П со сторонами, параллельными осям координат. Пусть функция f{x, у) непрерывна в прямоугольнике П. Двойной интеграл можно интерпретировать как (алгебраический) объем цилиндрического тела с основанием П, ограниченного поверхностью Рассмотрим соответствующее цилиндрическое тело. Проведем плоскость перпендикулярную оси Оу (рис.4). Эта плоскость рассечет цилиндрическое тело по криволинейной трапеции, ограниченной сверху плоской линией z, описываемой уравнениями Площадь трапеции АВВ\А\ выражается интегралом где интегрирование производится по х, а уо - второй аргумент подынтегральной функции - рассматривается при этом как постоянный (с ^ Уо ^ d). Величина интеграла (1) зависит от выбора значения уо. Положим (2) Выражение (2) дает площадь поперечного сечения цилиндрического тел а как функции от у. Поэтому объем цилиндрического тела можно вычислить по формуле С другой стороны, этот объем выражается двойным интегралом от функции /(ж, у) по прямоугольнику П. Значит, Заменяя S(y) его выражением (2), получим Задача, приводящая к понятию двойного интеграла Определение двойного интеграла Основные свойства двойного интеграла Площадь плоской области Сведение двойного интеграла к повторному Замена переменных в двойном интеграле Элемент площади в криволинейных координатах Якобиан и его геометрический смысл Формула замены переменных в двойном интеграле Двойной интеграл в полярных координатах Последнее соотношение обычно записывается так Объем цилиндрического тела можно отыскать также по площадям сечений плоскостями х = х0. Это приводит к формуле (4) Каждое из выражений, стоящих в правых частях формул (3) и (4), содержит две последовательные операции обыкновенного интегрирования функции /(ж, у). Они называются повторными интегралами от функции /(ж, у) по области П. Если /(ж, у) непрерывна в замкнутом прямоугольнике П, то переход к повторным интегралам всегда возможен и (5) т. е. значения повторных интегралов от непрерывной функции /(ж, у) не зависят от порядка интегрирования. Пример 1. Найти двойной интеграл от функции по области Имеем (см. рис. 5): 3.2. Случай произвольной области Предположим теперь, что областью интегрирования является произвольная ограниченная квадрируемая зам к нута я область D на плоскости хОу, удовлетворяющая следующему условию: любая прямая, параллельная оси Оу, пересекает границу области D не более чем в двух точках или по целому отрезку (рис. 6 а). Заключим область D внутрь прямоугольника так, как показано на рис. 66. Отрезок [а, 6] является ортогональной проекцией области D на ось Оху а отрезок [с, dj - ортогональной проекцией области D на ось Оу. Точками А и С граница области D разбивается на две кривые ABC и АЕС. Каждая из этих кривых пересекается с произвольной прямой, параллельной оси Оу, не более чем в одной точке. Поэтому их уравнения можно записать в форме, разрешенной относительно у: Пусть f{x, у) - некоторая функция, непрерывная в области D. Рассечем рассматриваемое цилиндрическое тело плоскостью. В сечении получим криволинейную трапецию PQMN (рис.7), площадь которой выражается обыкновенным интегралом от функции /(х, у), рассматриваемой как функция одной переменной у. При этом переменная у изменяется от ординаты точки Р до ординаты точки Q\ точка Р естьто*!-ка «входа» прямой х = const (в плоскости) в область - точка ее «выхода» из этой области. Так как уравнение кривой ABC есть, а кривой то эти ординаты при взятом х соответственно равны. Следовательно, интеграл дает нам выражение для площади плоского сечения цилиндрического тела как функции положения секущей плоскости х = const. Объем всего тела будет равен интегралу от этого выражения по ж в промежутке изменения. Таким образом, В частности, для площади S области D получим Предположим теперь, что каждая прямая пересекает границу области D не более чем в двух точках Р и Q, абсциссы которых равны соответственно (или по целому отрезку) (рис. 8). Проводя аналогичные рассуждения, приходим к формуле также сводящей вычисление двойного интеграла к повторному. Пример 2. Вычислить двойной интеграл от функции по области D. ограниченной линиями ^ Первый способ. Изобразим область интегрирования D. Прямая у = х и парабола у = х2 пересекаются в точках). Значит, х изменяется 8 пределах от 0 Любая прямая х = const) пересекает границу области не более чем в двух точках. Поэтому применима формула (8): Второй способ (рис. 10). Применяя формулу (10). получим тот же результат: Пример 3. Вычислить обьем тела, ограниченного поверхностью пересекается с плоскостью хОу по линии эллипс с полуосями в силу симметрии данного тела относительно координатных плоскостей жОж и у Ох получаем: Замечание. Если область D такова, что некоторые прямые (осртекальны е или горизонтальные) пересекают ее границу более чем в двух точках, то для вычисления двойного интеграла по области D следует разбитьее подходящим образом на части, свссгм к повторному каяцый из интегралов поэтом частям и полученные результаты сложить. Пример 4. Вычислить двойной интеграл по области D, заключенной между двумя квадратами с центрам и в начале координат и сторонами, параллельными осям координат, если сторона внутреннего квадрата равна 2, а внешнего - 4. непрерывна как в большом квадрате Q, сторона которого равна 4, так и в малом квадрате Р. сторона которого равна 2 (рис. 12). Согласно теореме 1, интегралы от функции е*** по указанным квадратам существуют, так что величина искомого интеграла §4. Замена переменных в двойном интеграле 4.1. Понятие криволинейных координат точки Пусть в области D* плоскости uOv задана пара фунмдий которые м ы будем считать непрерывными в этой области и имеющими непрерывные частные производные. В силу уравнения (1) кажд ой точке М*(«, v) области D* отвечает одна определенная точка М(х, у) в плоскости хОу и тем самым точкам области D* отвечает некоторое множество D точек (ж, у) в плоскости хОу (рис. 13). При этом говорят, что функции (1) осуществляют отображение области D4 на множество D. Предположим, что различным точкам (u, v) отвечают различные точки (х,у). Это равносильно однозначной разрешимости уравнений (1) относительно u, v: В этом случае отображение называется взаимно однозначным отображением области D* на область D. При таком преобразовании любая непрерывная кривая L*, лежащая в области D*, перейдет в непрерывную кривую L, лежащую в области D. Если функции д(х} у) и h(x, у) также непрерывны, то любая непрерывная линия LCD с помощью преобразования (2) перейдете непрерывную линию L* С D*. По заданной паре Щ, Vo значений переменных и, v из области D* можнооднознач-ноопределитьнетолькоположениеточки M*(u<)> Vq) в самой области £)*,нои положение соответствующей точии М(хо, уо) в области D, хо = 4>(ио, v0), 3/0 = o,vo). Это дает основание рассматривать числа u, v как некоторые новые координаты точки D области М на плоскости хОу. Их называют криволинейными координатами точки М. Множество точек области D, у которых одна из коорди нат сохраняет постоянное значение, называют координатной линией. Полагая в формуле (1) и = vq, получим параметрические уравнения координатной линии, Здесь роль параметра играет переменная и. Придавая координате v различные (возможные для нее) постоянные значения, получим семейство координатных линий (v = const) на плоскости хОу. Аналогично получаем и другое семейство координатных линий (и = const). При наличии взаимно однозначного соответств ия между областями D* и D различные координатные линии одного и того же семейства не пересекаются между собой, и через любую точку области D проходит по одной линии из каждого семейства. Сетка криволинейных координатных линий на плоскости хОр является образом прямоугольной сетки на плоскости uOv (см. рис. 13). 4.2. Элемент площади в криволинейных координатах. Якобиан и его геометрический смысл Выделим в области D* на плоскости Uo*V малый прямоугольник P*P?P$Pl со сторонами, параллельными осям координат 0*и и О" v и длинами сторон Аи и Av (для определенности считаем, что А) соответс твенно (рис. 14 а). Его площадь Прямоугольник переходит в криволинейный четырехугольник * в области D (рис. 146). Если вершины Р) имеют координаты, то,согласно формулам (1), соответствующие им вершины Pi имеют координаты), Пользуясь формулой Тейлора для функции двух переменных и ограничиваясь членами первого поря/рса огносительно Аи и Av, получим следующие приближенные значения координат для вершин четырехугольника где функции все их производные вычислены в точке). Найденные выражения для координат точек показывают, что с точностью до малых высшего порядка четырехугольник P\PiPiPa есть параллелограмм. Это следует изтого, что Тогда площадь ДS четырехугольника можно приближенно выразить через длину векторного произведения, Задача, приводящая к понятию двойного интеграла Определение двойного интеграла Основные свойства двойного интеграла Площадь плоской области Сведение двойного интеграла к повторному Замена переменных в двойном интеграле Элемент площади в криволинейных координатах Якобиан и его геометрический смысл Формула замены переменных в двойном интеграле Двойной интеграл в полярных координатах Определитель Из формул (7) и (8) видео, что абсолютная величина якобиана играет роль локального коэффициента растяжения области D" (в данной точке (tx, v)) при отображении ее на область D при помощи формул преобразования (1). 4.3. Формула замены переменных в двойном интеграле Пусть непрерывные функции осуществляют взаимнооднозначное отображение области D* на D и имеют непрерывные частные производные первого порядка. Пусть в области D на плоскости хОу задана непрерывная функция Каждому значению функции) в области D соответствует равное значение функции г = в области D", где. Разобьем область D* на частичные области и построим соответствующее разбиение области D. Выберем в соответствующих частичных областях точки (и, v) и (ж, у) так, чтобы значения функций в них совпадали, и составим интегральные суммы для функций z = /(ж, у) и v) по областям D и D*. Получим якобиан функций. Переходя в равенстве (9) к пределу при стремлении к нулю наибольшего диаметра d* частичных областей D\ (в силу непрерывности отображения (I) будет стремиться к нулю и наибольший из диаметров d частичных областей в D), будем иметь где Условие J Ф 0 является условием локальной взаимнооднозначности отображения, осуществляемого функциями Теорема 4. Дгя того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции /(ж, у) переменные ж и у соответственно через а элемент площади dx dy - его выражением в криволинейных координатах: Пример. Найти площадь фигуры, ограниченной гиперболами м Отыскание площади указанной фигуры сводупся к вычислению двойного интеграла по области О. Введем новые, криволинейные координаты и и о формулами Из условия аадачи ясио, что. Значит, в плоскости uOv мы получили прямоугольник (рис. 156) - фигуру более простую, чем заданная фигура D. Выразим х и у из соотношений (11) через и и t>: Рис.15 Тогда Двойной интеграл в полярных координатах Вычисление двойного интеграла часто упрощается заменой прямоугольных координат х и у полярными координатами по формулам Элемент площади в полярных координатах имеет вид и формулу перехода от интеграла в декартовых координатах к интегралу в полярных координатах можно записать так: В этом случае (13) Элемент площади в полярных координатах можно получить и из геометрических соображений (см. рис. 16). Площадь заштрихованной на рисунке области А = пл. сектора. сектора Отбрасывая бесконечно малую величину высшего порядка, получаем и принимаем за элемент площади в полярных координатах. Итак, чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно а: и у в подынтегральной функции заменить соответственно через р costp и psiny, а элементплощади в декартовых координатах dx dy заменить элементом площади в полярных координатах р dp dip. Займемся теперь вычислением двойного интеграла в полярных координатах. Как и в случае прямоугольных декартовых координат, вычисление интеграла в полярных координатах осуществляется путем сведения его к повторному интегралу. Рассмотрим сначала случай, когда полюс О лежит вне заданной области D. Пусть область D обладает тем свойством, что любой луч, исходящий из полюса (координатная линия у пересекает ее границу не более чем в двух точках или по целому отрезку (рис. 17). Отметим крайние значения i полярного угла являются пределами внешнего интегрирования. Луч ц> = проходит через точку А контура области D, а луч через точку В. Точки Aw В разбивают контур области D на две части: АСВ и AFB. Пусть - их полярные уравнения, причем) - однозначные непрерывные функции удовлетворяющие условию Функции являются пределами внутреннего интегрирования. Переходя к повторным интегралам, получаем следующую формулу В частности, для площади S области D при F(p, г 1 получаем Пустьтеперьполюс О расположен внутри области D. Предположим, чтообласть D является звездной относительно полюса, т. е. любой луч tp = const пересекает границу области только в одной точке или по целрму отрезку (рис. 18). Пусть - уравнение границы области в полярных координатах. Тогда Рис. 18 Пример. Вычислить интеграл где область - четверть единичного круга, расположенная в первом квадранте. Перейдем к полярным координатам Тогда областью интегрирования будет прямоугольник Преобразованный интеграл / легко вычисляется: г Замечание. Если якобиан отличен от нуля в области D, то отображение в некоторой окрестности каждой точки этой области является взаимнооднозначным. При этом может, однако, случиться, что отображение всей области не будет взаимнооднозначным. Рассмотрим отображение, определяемое функциями Якобиан этих функций равен и, следовательно, везде отличен от нуля. Несмотря на это, для мы получим, так что это отображение не является взаимнооднозначным. С другой стороны, если якобиан отображения обращается в нуль в какой-нибудь точке, то, тем не менее, отображение в окрестности этой точки может оказаться взаимно однозначным. Например, для отображения, определяемого функциями якобиан равен нулю и при, но отображение является взаимнооднозначным. Обратное отображение определяется функциями

1.1 Определение двойного интеграла

1.2 Свойства двойного интеграла

1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D 1 и D 2 , то функция f(x, y) интегрируема в каждой из областей D 1 и D 2 , причем

2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а? и? - любые вещественные числа, то функция [? · f(x, y) + ?· g(x, y)] также интегрируема в области D, причем

3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ? g(x, y), то

5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)

6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число?, удовлетворяющее неравенству m ? ? ? M и такое, что справедлива формула

В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (?, ?), что? = f(?, ?), и формула принимает вид

7°. Важное геометрическое свойство. равен площади области D

Пусть в пространстве дано тело T (рис. 2.1), ограниченное снизу областью D , сверху - графиком непрерывной и неотрицательной функции) z=f (x, y ,) которая определена в области D , с боков - цилиндрической поверхностью, направляющей которой является граница области D , а образующие параллельны оси Оz. Тело такого вида называется цилиндрическим телом.

1.3 Геометрическая интерпретация двойного интеграла

1.4 Понятие двойного интеграла для прямоугольника

Пусть произвольная функция f(x, y) определена всюду на прямоугольнике R = ? (см. Рис. 1).

Разобьем сегмент a ? x ? b на n частичных сегментов при помощи точек a = x 0 < x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Этому разбиению при помощи прямых, параллельных осям Ox и Oy, соответствует разбиение прямоугольника R на n · p частичных прямоугольников R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Указанное разбиение прямоугольника R обозначим символом T. В дальнейшем в этом разделе под термином "прямоугольник" будем понимать прямоугольник со сторонами, параллельными координатным осям.

На каждом частичном прямоугольнике R kl выберем произвольную точку (? k , ? l). Положив?x k = x k - x k-1 , ?y l = y l - y l-1 , обозначим через?R kl площадь прямоугольника R kl . Очевидно, ?R kl = ?x k ?y l .

называется интегральной суммой функции f(x, y), соответствующей данному разбиению T прямоугольника R и данному выбору промежуточных точек (? k , ? l) на частичных прямоугольниках разбиения T.

Диагональ будем называть диаметром прямоугольника R kl . Символом? обозначим наибольший из диаметров всех частичных прямоугольников R kl .

Число I называется пределом интегральных сумм (1) при? > 0, если для любого положительного числа? можно указать такое положительное число?, что при? < ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - I | < ?.

Функция f(x, y) называется интегрируемой (по Риману) на прямоугольнике R, если существует конечный предел I интегральных сумм этой функции при? > 0.

Указанный предел I называется двойным интегралом от функции f(x, y) по прямоугольнику R и обозначается одним из следующих символов:

Замечание. Точно также, как и для однократного определенного интеграла, устанавливается, что любая интегрируемая на прямоугольнике R функция f(x, y) является ограниченной на этом прямоугольнике.

Это дает основание рассматривать в дальнейшем лишь ограниченные функции f(x, y).

Задача, приводящая к понятию двойного интеграла.

Предположим, что на определена функция частей и запишем сумму

которая именуется интегральной.

О: Под определенным интегралом (о.и.) от функции и от выбора

Обозначение:

Числа именуют интегрируемой (по Риману) на .

Т. существования: При условии, что .

В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида , пределов и , однако не зависит от символа обозначения переменной , иначе выражаясь

В соответствии с п.17.1.1 и 17.1.2 и определением о.и. запишем формулы площади криволинейной трапеции: , работы силы

на :

Понятие двойного интеграла, интегральных сумм.

Существование двойного интеграла, т. е. предела интегральной суммы для кажется очевидным, так как этот предел дает объем цилиндрического тела. Однако это рассуждение не является строгим. В более полных курсах это утверждение строго доказывается и носит название теоремы существования двойного интеграла.

Теорема существования. Для всякой функции, непрерывной в ограниченной замкнутой области, имеющей площадь а, существует двойной интеграл, т. е. существует предел интегральных сумм при неограниченном увеличении числа малых площадок при условии, что каждая из них стягивается в точку. Этот предел не зависит ни от способа разбиения области а на части ни от выбора точек

В дальнейшем мы будем рассматривать только функции, непрерывные в области интегрирования.

Из теоремы существования следует, что мы можем, например, разбить область а на малые прямоугольники со сторонами прямыми, параллельными осям координат (рис. 230). При этом. Выбирая затем в каждом малом прямоугольнике по точке мы можем написать, согласно определению двойного интеграла

Для того чтобы подчеркнуть, что двойной интеграл можно получить как предел суммы вида вместо обозначения употребляют также обозначение

Выражение называется элементом площади в декартовых координатах и равно площади прямоугольника со сторонами параллельными координатным осям.

Заметим, что при составлении интегральной суммы площадки прилегающие к границе области а, не имеют формы прямоугольников. Однако можно доказать, что ошибка от замены таких площадок прямоугольниками с площадями в пределе сведется к нулю.

Свойства двойных интегралов

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

В частности, если функция f (x , y ) непрерывна в D , а область D связна , то в этой области найдется такая точка (ξ , η ), что μ = f (ξ , η ), и формула (11) принимает вид

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

Пример 2. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

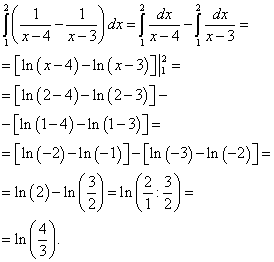
Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем первое слагаемое:

Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

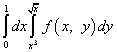Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

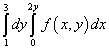Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .

Возможно, будет полезно почитать: