Grundlegende Eigenschaften des Doppelintegrals. Die Aufgabe des Doppelintegrals ist die Definition der Haupteigenschaften des Doppelintegrals. Grundkonzepte und Definitionen des Doppelintegrals

Grundlegende Eigenschaften des Doppelintegrals

Die Eigenschaften des Doppelintegrals (und ihre Ableitung) ähneln den entsprechenden Eigenschaften des einfach definiten Integrals.

1°. Additivität. Wenn die Funktion F(X, j) ist in die Domäne integrierbar D und wenn die Gegend D mithilfe einer Kurve G der Fläche Null ist in zwei verbundene Regionen ohne gemeinsame Innenpunkte unterteilt D 1 und D 2 , dann die Funktion F(X, j) ist in jede der Domänen integrierbar D 1 und D 2 und

2°. Lineare Eigenschaft. Wenn funktioniert F(X, j) Und G(X, j) sind in die Domäne integrierbar D, A α Und β Gibt es reelle Zahlen, dann ist die Funktion [ α · F(X, j) + β · G(X, j)] ist ebenfalls in die Domäne integrierbar D, Und

3°. Wenn funktioniert F(X, j) Und G(X, j) sind in die Domäne integrierbar D, dann ist das Produkt dieser Funktionen auch in integrierbar D.

4°. Wenn funktioniert F(X, j) Und G(X, j) sind beide in die Domäne integrierbar D und überall in dieser Gegend F(X, j) ≤ G(X, j), Das

5°. Wenn die Funktion F(X, j) ist in die Domäne integrierbar D, dann ist die Funktion | F(X, j)| in die Umgebung integrierbar D, Und

(Natürlich aus der Integrierbarkeit | F(X, j)| V D Integrierbarkeit folgt nicht F(X, j) V D.)

6°. Mittelwertsatz. Wenn beides funktioniert F(X, j) Und G(X, j) sind in die Domäne integrierbar D, Funktion G(X, j) ist überall in dieser Region nicht negativ (nicht positiv), M Und M- genaue Ober- und Untergrenzen der Funktion F(X, j) im Gebiet D, dann gibt es eine Zahl μ , wodurch die Ungleichung erfüllt wird M ≤ μ ≤ M und so, dass die Formel

Problem, das zum Konzept eines Doppelintegrals führt Definition eines Doppelintegrals Grundeigenschaften eines Doppelintegrals Fläche einer flachen Region Reduktion eines Doppelintegrals auf eine iterierte Änderung von Variablen in einem Doppelintegral Flächenelement in krummlinigen Koordinaten Jacobi und seine geometrische Bedeutung Änderung der Variablenformel in einem Doppelintegral Doppelintegral in Polarkoordinaten

Ein Problem, das zum Konzept eines Doppelintegrals führt. Definition des Doppelintegrals. Wir kommen zum Konzept eines Doppelintegrals, indem wir ein spezifisches Problem der Berechnung des Volumens eines zylindrischen Körpers lösen. Ein zylindrischer Körper ist ein Körper, der durch die xOy-Ebene, eine Fläche und eine Zylinderfläche begrenzt wird, deren Erzeuger parallel zur Achse liegen (siehe Abb. 1). Die Fläche D der Änderung der Variablen x und y wird Grundfläche des zylindrischen Körpers genannt. Bei der Bestimmung des Körpervolumens gehen wir von zwei Prinzipien aus: !) Ist der Körper in Teile geteilt, dann ist sein Volumen gleich der Summe der Volumina aller Teile (Additivitätseigenschaft); 2) Das Volumen eines geraden Zylinders, der durch eine Ebene z = const begrenzt wird, die parallel zur xOy-Ebene verläuft, ist gleich der Grundfläche multipliziert mit der Höhe. Im Folgenden gehen wir davon aus, dass der Bereich D zusammenhängend (aus einem Stück bestehend), quadrierbar (d. h. mit einer Fläche) und begrenzt (d. h. innerhalb eines Kreises mit Mittelpunkt im Ursprung) ist. Sei eine stetige Funktion des Punktes P(x, y) im Bereich überall im Bereich Z>, d. h. dass die betrachtete Zylinderfläche vollständig über der xOy-Ebene liegt. Wir bezeichnen das Volumen des zylindrischen Körpers mit V. Teilen wir den Bereich D – die Basis des zylindrischen Körpers – in eine bestimmte Anzahl n sich nicht schneidender quadratischer Bereiche beliebiger Form; wir nennen sie Teilregionen. Nachdem die Teilregionen in einer bestimmten Reihenfolge nummeriert wurden, werden die Gebiete jeweils durchnummeriert. Wir nennen den Durchmesser eines Teilbereichs Dk die Größe. Problem, das zum Konzept eines Doppelintegrals führt. Definition eines Doppelintegrals. Grundeigenschaften eines Doppelintegrals. Fläche eines flachen Bereichs. Reduktion eines Doppelintegrals auf eine iterierte Änderung von Variablen in einem Doppelintegral Flächenelement in krummlinigen Koordinaten Jacobi und seine geometrische Bedeutung Änderung der Variablenformel in einem Doppelintegral Doppelintegral in Polarkoordinaten, wobei das Symbol p(P; Q) den Abstand zwischen den Punkten P und Q bezeichnet. Sei d die größter Durchmesser der Teilbereiche Dk (k = 1,2,...,n). Zeichnen wir eine Zylinderfläche durch die Grenze jedes Teilbereichs mit Generatoren parallel zur Oz-Achse. Dadurch wird der zylindrische Körper in n zylindrische Teilkörper unterteilt. Ersetzen wir den k-ten Teilkörper durch einen geraden Zylinder mit gleicher Grundfläche und einer Höhe gleich der Anwendung eines Punktes der ersetzten Oberfläche (Abb. 2). Das Volumen eines solchen Zylinders ist, wobei der Punkt die Fläche der Region Dk ist. Nachdem wir die beschriebenen Konstruktionen für jeden Teilzylinderkörper durchgeführt haben, erhalten wir einen n-stufigen Körper, dessen Volumen (o) Es ist intuitiv klar, dass Vn das gewünschte Volumen V umso genauer ausdrückt, je kleiner die Abmessungen der Teilbereiche Dk sind . Wir nehmen das Volumen V des zylindrischen Körpers als gleich der Grenze an, zu der das Volumen (1) des n-stufigen Körpers tendiert, da der größte Durchmesser d der Teilbereiche Dk gegen Null n geht. Natürlich sollte die Grenze nicht von der Art der Aufteilung des Gebietes D in Teilgebiete Dk und von der Wahl der Punkte Pk in den Teilgebieten abhängen. Sei f(x, y) eine beliebige Funktion, die in der Domäne D definiert ist. Die Summe n (1) wird als Integralsumme für die Funktion f(x)y) über die Domäne D bezeichnet, die einer gegebenen Partition dieser Domäne entspricht n Teilgebiete und eine gegebene Auswahl an Punkten ®*,!/*) auf Teilgebieten Dk. Definition. Wenn es für d - * 0 einen Grenzwert von Integralsummen n gibt, der weder von der Methode zur Aufteilung des Gebiets D in Teilgebiete noch von der Wahl der Punkte Pk in den Teilgebieten abhängt, dann heißt er Doppelintegral von die Funktion f(P) (oder f(x, y )) über dem Definitionsbereich D und wird mit dem Symbol OR bezeichnet. Also (2) Die Funktion f(x, y) selbst heißt im Definitionsbereich D integrierbar (f( P) ist der Integrand, f(P) dS ist der Integrand, dS ist das Differential (oder Element) der Fläche, der Bereich D ist der Integrationsbereich; der Punkt P (®, y) ist die Variable Feinintegration) . ,.. Zurück zum zylindrischen Körper kommen wir zu dem Schluss: Das Volumen des zylindrischen Körpers, das durch die xOy-Ebene, die Oberfläche und die zylindrische Oberfläche mit Generatoren parallel zur Oz-Achse begrenzt wird, ist gleich dem Doppelintegral der Funktion f(x , y) über der Region D, die die Basis des zylindrischen Körpers ist. / ODER Hier ist dx dy das Flächenelement in kartesischen Koordinaten. Dies ist die geometrische Bedeutung des Doppelintegrals einer nichtnegativen Funktion. Wenn dann das Volumen If im Bereich D der Funktion f(P) sowohl positive als auch negative Werte annimmt, dann stellt das Integral die algebraische Summe der Volumina derjenigen Körperteile dar, die sich oberhalb der xOy-Ebene befinden (aufgenommen mit der). „+“-Zeichen) und diejenigen Körperteile, die sich unter der xOy-Ebene befinden (aufgenommen mit dem „-“-Zeichen). Zur Bildung von Summen der Form (1) für eine Funktion zweier unabhängiger Variablen und zum anschließenden Übergang zum Grenzwert führen eine Vielzahl von Problemen, nicht nur das Problem des Volumens eines zylindrischen Körpers. Formulieren wir hinreichende Bedingungen für die Integrierbarkeit. Satz 1. Jede Funktion y), die in einem begrenzten geschlossenen Bereich D stetig ist, ist in diesem Bereich integrierbar. Die Anforderung an die Kontinuität des Integranden ist oft zu restriktiv. Für Anwendungen ist der folgende Satz wichtig, der die Existenz eines Doppelintegrals für eine bestimmte Klasse diskontinuierlicher Funktionen garantiert. Wir werden sagen, dass eine Punktmenge in einer Ebene die Fläche Null hat, wenn sie in eine Polygonfigur mit beliebig kleiner Fläche eingeschlossen werden kann. Satz 2. Wenn eine Funktion f(x, y) in einem geschlossenen begrenzten Bereich D beschränkt und überall in D stetig ist, mit Ausnahme einer Menge von Punkten der Fläche Null, dann ist diese Funktion im Bereich D integrierbar. §2. Grundlegende Eigenschaften des Doppelintegrals Doppelintegrale haben eine Reihe ähnlicher Eigenschaften wie das bestimmte Integral für Funktionen einer unabhängigen Variablen. 2.1. Lineare Eigenschaft Wenn die Funktionen a) im Definitionsbereich D integrierbar sind und a und p beliebige reelle Zahlen sind, dann ist die Funktion af) auch im Definitionsbereich D integrierbar und o) 2.2. Integration von Ungleichungen Sind die Funktionen im Bereich D und überall in diesem Bereich integrierbar, so ist (2) d. h. die Ungleichungen integrierbar. Insbesondere durch die Integration der offensichtlichen Ungleichungen erhalten wir die Fläche einer flachen Region. Die Fläche einer flachen Region D ist gleich dem Doppelintegral über diese Region einer Funktion, die identisch gleich eins ist. Tatsächlich hat die Integralsumme für die Funktion /(P) = 1 im Bereich D die Form und ist für jede Aufteilung des Bereichs D in Teilbereiche Dt gleich seiner Fläche S. Aber dann ist der Grenzwert dieser Summe, d. h. , das Doppelintegral, ist gleich der Fläche S Domänen D: oder, was dasselbe ist, (3) 2.4. Schätzung des Integrals Die Funktion /(P) sei in einem begrenzten geschlossenen Bereich D stetig, M und mn seien die größten und kleinsten Werte von /(P) im Bereich D und 5 sei seine Fläche. Dann (4) 2.5. Additivität: Wenn die Funktion /(P) im Bereich D integrierbar ist und der Bereich Z) in zwei Bereiche D\ und Di ohne gemeinsame innere Punkte unterteilt ist, dann ist /(P) auf jedem der Bereiche D\ und Di integrierbar und (5) 2.6. Satz über den Mittelwert Satz 3 (über den Mittelwert). Wenn die Funktion /(P) in einem geschlossenen begrenzten Bereich D stetig ist, dann gibt es mindestens einen Punkt Pc des Bereichs D, so dass die Formel u gültig ist, wobei S die Fläche des Bereichs D ist, Domäne D, dann nimmt es in D seinen größten Wert M und seinen kleinsten Wert m an. Aufgrund der Eigenschaft 4 der Schätzung des Integrals P) im Bereich D nimmt es an einem Punkt Pc G D einen Wert an, der dieser Zahl entspricht, woraus S The Der durch Formel (7) bestimmte Wert f(Pc) wird als Mittelwert der Funktion f(P) im Bereich D bezeichnet. Wert Wenn im Bereich D die Funktion /(P) ^ O, dann bedeutet Formel (6). Es gibt einen geraden Zylinder mit einer Grundfläche D (dessen Fläche 5 beträgt) und einer Höhe H = /(Pc), dessen Volumen gleich dem Volumen eines zylindrischen Körpers ist (Abb. . 3). § 3. Reduktion eines Doppelintegrals auf ein iteriertes Integral Eine der effektivsten Methoden zur Berechnung eines Doppelintegrals besteht darin, es auf ein iteriertes Integral zu reduzieren. 3.1. Der Fall eines Rechtecks. Die Region D sei ein geschlossenes Rechteck Π mit Seiten parallel zu den Koordinatenachsen. Die Funktion f(x, y) sei im Rechteck P stetig. Das Doppelintegral kann als (algebraisches) Volumen eines zylindrischen Körpers interpretiert werden, dessen Basis P durch eine Fläche begrenzt wird. Betrachten Sie den entsprechenden zylindrischen Körper. Zeichnen wir eine Ebene senkrecht zur Oy-Achse (Abb. 4). Diese Ebene schneidet den zylindrischen Körper entlang eines krummlinigen Trapezes, das von oben durch eine flache Linie z begrenzt wird und durch die Gleichungen beschrieben wird. Die Fläche des Trapezes ABB\A\ wird durch das Integral ausgedrückt, bei dem die Integration über x und yo durchgeführt wird zweites Argument des Integranden - wird als Konstante betrachtet). Der Wert des Integrals (1) hängt von der Wahl des Wertes von y0 ab. Wir setzen (2). Ausdruck (2) gibt die Querschnittsfläche zylindrischer Körper a als Funktion von y an. Daher kann das Volumen eines zylindrischen Körpers durch die Formel berechnet werden. Andererseits wird dieses Volumen durch ein Doppelintegral der Funktion /(x, y) über dem Rechteck P ausgedrückt. Daher wird S(y) durch sein ersetzt Ausdruck (2) erhalten wir das Problem, das zum Konzept eines Doppelintegrals führt. Definition eines Doppelintegrals. Grundeigenschaften eines Doppelintegrals. Fläche einer flachen Region. Reduktion eines Doppelintegrals auf eine iterierte Änderung von Variablen in einem Doppel Integral Flächenelement in krummlinigen Koordinaten Jacobi und seine geometrische Bedeutung Änderung der Variablenformel in einem Doppelintegral Doppelintegral in Polarkoordinaten Die letzte Beziehung wird normalerweise wie folgt geschrieben: Das Volumen eines zylindrischen Körpers kann auch anhand der Querschnittsflächen ermittelt werden Ebenen x = x0. Dies führt zu Formel (4). Jeder der Ausdrücke auf der rechten Seite der Formeln (3) und (4) enthält zwei aufeinanderfolgende Operationen der gewöhnlichen Integration der Funktion f(x, y). Man nennt sie iterierte Integrale der Funktion f(x, y) über den Definitionsbereich Π. Wenn f(x, y) im geschlossenen Rechteck Π stetig ist, dann ist der Übergang zu iterierten Integralen immer möglich, und (5) d. h. die Werte der iterierten Integrale der stetigen Funktion /(x, y) hängen nicht von der Integrationsreihenfolge ab. Beispiel 1. Finden Sie das Doppelintegral einer Funktion über der Fläche. Wir haben (siehe Abb. 5): 3.2. Der Fall einer beliebigen Domäne Nehmen wir nun an, dass die Integrationsdomäne eine beliebige begrenzte quadrierte geschlossene Domäne D auf der xOy-Ebene ist, die die folgende Bedingung erfüllt: Jede gerade Linie parallel zur Oy-Achse schneidet die Grenze der Domäne D um nicht mehr als zwei Punkte oder entlang eines ganzen Segments (Abb. . 6 a). Wir schließen die Fläche D in das Rechteck ein, wie in Abb. 66. Das Segment [a, 6] ist eine orthogonale Projektion der Region D auf die Oxy-Achse, und das Segment [c, dj ist eine orthogonale Projektion der Region D auf die Oy-Achse. Durch die Punkte A und C wird die Grenze der Region D in zwei Kurven ABC und AEC unterteilt. Jede dieser Kurven schneidet eine beliebige Gerade parallel zur Oy-Achse an höchstens einem Punkt. Daher können ihre Gleichungen in der für y zulässigen Form geschrieben werden: Sei f(x, y) eine im Bereich D stetige Funktion. Schneiden wir den betrachteten zylindrischen Körper durch eine Ebene. In diesem Abschnitt erhalten wir ein krummliniges Trapez PQMN (Abb. 7), dessen Fläche durch ein gewöhnliches Integral der Funktion / (x, y) ausgedrückt wird, betrachtet als Funktion einer Variablen y. In diesem Fall ändert sich die Variable y von der Ordinate des Punktes P zur Ordinate des Punktes Q\ Punkt P ist der *!-ka „Eingang“ der Geraden x = const (in der Ebene) in den Bereich – der Punkt seines „Austritts“ aus dieser Region. Da es eine Gleichung für die ABC-Kurve und für die Kurve gibt, sind diese Ordinaten jeweils gleich, wenn x genommen wird. Daher gibt uns das Integral einen Ausdruck für die Fläche eines flachen Abschnitts eines zylindrischen Körpers als Funktion der Position der Sekantenebene x = const. Das Volumen des gesamten Körpers wird im Änderungsintervall gleich dem Integral dieses Ausdrucks über w sein. Somit erhalten wir insbesondere für die Fläche S der Region D. Nehmen wir nun an, dass jede Linie die Grenze der Region D an nicht mehr als zwei Punkten P und Q schneidet, deren Abszissen jeweils gleich sind (oder entlang). ein ganzes Segment) (Abb. 8). Wenn wir ähnliche Überlegungen anstellen, kommen wir zu einer Formel, die auch die Berechnung des Doppelintegrals auf eine wiederholte reduziert. Beispiel 2. Berechnen Sie das Doppelintegral einer Funktion über die durch Linien begrenzte Fläche D. ^ Der erste Weg. Stellen wir den Integrationsbereich D dar. Die Gerade y = x und die Parabel y = x2 schneiden sich in Punkten. Dies bedeutet, dass sich x innerhalb von 8 Grenzen von 0 ändert. Jede Gerade (x = const) schneidet die Grenze der Region in höchstens zwei Punkten. Daher ist Formel (8) anwendbar: Die zweite Methode (Abb. 10). Anwendung der Formel (10). Wir erhalten das gleiche Ergebnis: Beispiel 3. Berechnen Sie das Volumen eines Körpers, der von einer Oberfläche begrenzt wird, die die xOy-Ebene entlang der Ellipsenlinie mit Halbachsen schneidet. Aufgrund der Symmetrie dieses Körpers in Bezug auf die xOx- und y-Koordinatenebenen erhalten wir: Anmerkung. Wenn das Gebiet D so beschaffen ist, dass einige gerade Linien (entweder orthogonal oder horizontal) seine Grenze in mehr als zwei Punkten schneiden, dann ist es zur Berechnung des Doppelintegrals über das Gebiet D erforderlich, es auf geeignete Weise in Teile zu unterteilen Wiederholen Sie die Integration der Integrale in Teile und addieren Sie die Ergebnisse. Beispiel 4. Berechnen Sie das Doppelintegral über die Fläche D, eingeschlossen zwischen zwei Quadraten mit Mittelpunkten und im Ursprung und an den Seiten parallel zu den Koordinatenachsen, wenn die Seite des inneren Quadrats 2 und die äußere 4 ist. ist stetig als in einem großen Quadrat Q, dessen Seite 4 ist, und in dem kleinen Quadrat R., dessen Seite gleich 2 ist (Abb. 12). Nach Satz 1 existieren die Integrale der Funktion e*** über die angegebenen Quadrate, so dass sich der Wert des gesuchten Integrals §4 ergibt. Änderung der Variablen im Doppelintegral 4.1. Das Konzept der krummlinigen Koordinaten eines Punktes Es sei ein Funktionspaar im Bereich D* der Ebene uOv gegeben, das wir in diesem Bereich als stetig betrachten und stetige partielle Ableitungen haben. Aufgrund der Gleichung (1) entspricht jeder Punkt M*(x, v) der Region D* einem bestimmten Punkt M(x, y) in der xOy-Ebene und damit den dortigen Punkten der Region D* eine bestimmte Menge D von Punkten (x, y) in der xy-Ebene (Abb. 13). In diesem Fall soll die Funktion (1) die Region D4 auf die Menge D abbilden. Nehmen wir an, dass verschiedene Punkte (u, v) verschiedenen Punkten (x, y) entsprechen. Dies ist äquivalent zur eindeutigen Lösbarkeit der Gleichungen (1) bezüglich u, v: In diesem Fall nennt man die Abbildung eine Eins-zu-Eins-Abbildung des Bereichs D* auf den Bereich D. Unter einer solchen Transformation gilt: any Die kontinuierliche Kurve L*, die im Bereich D* liegt, geht in eine kontinuierliche Kurve L über, die im Bereich D liegt. Wenn die Funktionen q(x), y) und h(x, y) ebenfalls kontinuierlich sind, verwendet jede kontinuierliche Linie LCD eine Transformation (2) geht über die durchgezogene Linie L* C D*. Für ein gegebenes Paar W, Vo der Werte der Variablen u, v aus der Region D* ist es möglich, nicht nur die Position des Punktes M*(u) eindeutig zu bestimmen<)> Vq) im Bereich ξ)* selbst, sondern die Position des entsprechenden Punktes M(xo, yo) im Bereich D, xo = 4>(o, v0), 3/0 = o, vo). Dies gibt Anlass, die Zahlen u, v als einige neue Koordinaten des Punktes D der Region M auf der xOy-Ebene zu betrachten. Sie werden als krummlinige Koordinaten des Punktes M bezeichnet. Die Menge der Punkte im Bereich D, für die eine der Koordinaten konstant bleibt, wird als Koordinatenlinie bezeichnet. Unter der Annahme in Formel (1) u = vq erhalten wir die parametrischen Gleichungen der Koordinatenlinie. Hier spielt die Variable u die Rolle des Parameters. Wenn wir der Koordinate v verschiedene (für sie mögliche) konstante Werte geben, erhalten wir eine Familie von Koordinatenlinien (v = const) auf der xOy-Ebene. Auf ähnliche Weise erhalten wir eine weitere Familie von Koordinatenlinien (u = const). Wenn zwischen den Regionen D* und D eine Eins-zu-eins-Entsprechung besteht, schneiden sich verschiedene Koordinatenlinien derselben Familie nicht, und eine Linie aus jeder Familie verläuft durch einen beliebigen Punkt der Region D. Das Gitter der krummlinigen Koordinatenlinien auf der xOp-Ebene ist das Bild eines rechteckigen Gitters auf der uOv-Ebene (siehe Abb. 13). 4.2. Flächenelement in krummlinigen Koordinaten. Die Jacobi-Einheit und ihre geometrische Bedeutung. Wir markieren im Bereich D* auf der Ebene Uo*V ein kleines Rechteck P*P?P$Pl mit Seiten parallel zu den Koordinatenachsen 0*u und O"v und den Längen der Seiten Au und Av (aus Gründen der Bestimmtheit nehmen wir an, dass A ) bzw. (Abb. 14 a). Seine Fläche Das Rechteck geht im Bereich D in ein krummliniges Viereck * über (Abb. 146). Wenn die Eckpunkte P) Koordinaten haben, dann , gemäß Formeln (1) haben die entsprechenden Eckpunkte Pi Koordinaten), Wenn wir die Taylor-Formel für eine Funktion zweier Variablen verwenden und uns auf die Terme erster Ordnung / pc bezüglich Au und Av beschränken, erhalten wir die folgende Näherung Werte der Koordinaten für die Eckpunkte des Vierecks, wobei die Funktionen und alle ihre Ableitungen an einem Punkt berechnet werden. Ordnungsviereck P\PiPiPa ist ein Parallelogramm. Dies folgt aus der Tatsache, dass dann die Fläche DS des Vierecks näherungsweise ausgedrückt werden kann in Bezug auf die Länge des Vektorprodukts, Problem, das zum Konzept eines Doppelintegrals führt Definition eines Doppelintegrals Grundeigenschaften eines Doppelintegrals Fläche einer flachen Region Reduktion eines Doppelintegrals auf eine iterierte Änderung von Variablen in Doppelintegral Flächenelement in krummlinigen Koordinaten Jacobian und seine geometrische Bedeutung Änderung der Variablenformel im Doppelintegral Doppelintegral in Polarkoordinaten Determinantpunkt (tx, v)), wenn er mithilfe der Transformationsformeln (1) auf den Bereich D abgebildet wird. 4.3. Formel zur Änderung der Variablen im Doppelintegral. Stetige Funktionen führen eine Eins-zu-Eins-Abbildung des Definitionsbereichs D* auf D durch und haben stetige partielle Ableitungen erster Ordnung. Es sei eine stetige Funktion im Bereich D auf der xOy-Ebene gegeben. Jeder Wert der Funktion) im Bereich D entspricht einem gleichen Wert der Funktion r = im Bereich D, wobei (u, v) und (x , y) so dass die Werte der darin enthaltenen Funktionen übereinstimmen, und wir bilden die Integralsummen für die Funktionen z = /(x, y) und v) über den Domänen D und D*. Wir erhalten die Jacobi-Funktion der Funktionen. (9) bis zum Grenzwert, da der größte Durchmesser d* der Teilbereiche D\ gegen Null tendiert (aufgrund der Kontinuität der Abbildung (I) wird auch der größte der Durchmesser d der Teilbereiche in D gegen Null tendieren auf Null) haben wir, wobei Bedingung J Ф 0 die Bedingung Satz 4 ist. Um das in kartesischen Koordinaten angegebene Doppelintegral in ein Doppelintegral in krummlinigen Koordinaten umzuwandeln, müssen die Variablen x und y im Integranden von ersetzt werden f(x, y) jeweils durch und das Flächenelement dx dy - sein Ausdruck in krummlinigen Koordinaten: Beispiel. Finden Sie die Fläche einer durch Hyperbeln begrenzten Figur m. Das Ermitteln der Fläche der angegebenen Figur reduziert sich auf die Berechnung eines Doppelintegrals über die Region O. Lassen Sie uns durch die Formeln neue, krummlinige Koordinaten u und o einführen Das bedeutet, dass wir in der uOv-Ebene ein Rechteck erhalten (Abb. 156) – eine Figur, die einfacher ist als die gegebene Figur D. Lassen Sie uns x und y aus den Beziehungen (11) durch u und t> ausdrücken: Abb. 15 Dann Doppelintegral in Polar Koordinaten Die Berechnung des Doppelintegrals wird oft vereinfacht, indem die rechtwinkligen Koordinaten x und y durch Polarkoordinaten gemäß den Formeln ersetzt werden. Das Flächenelement in Polarkoordinaten hat die Form und die Formel für den Übergang vom Integral in kartesischen Koordinaten zum Integral in Polarkoordinaten kann wie folgt geschrieben werden: In diesem Fall (13) kann das Flächenelement in Polarkoordinaten aus geometrischen Überlegungen gewonnen werden (siehe Abb. 16). Die Fläche des in der Abbildung schattierten Bereichs A \u003d pl. Sektoren. Sektoren Wenn wir einen Infinitesimalwert höherer Ordnung verwerfen, erhalten wir ein Flächenelement und akzeptieren es als Flächenelement in Polarkoordinaten. Um also das Doppelintegral in kartesischen Koordinaten in ein Doppelintegral in Polarkoordinaten umzuwandeln, müssen Sie a: und y im Integranden durch p costp bzw. psiny ersetzen und das Flächenelement in kartesischen Koordinaten dx dy durch die Fläche ersetzen Element in Polarkoordinaten p dp dip. Kommen wir nun zur Berechnung des Doppelintegrals in Polarkoordinaten. Wie bei rechtwinkligen kartesischen Koordinaten erfolgt die Berechnung des Integrals in Polarkoordinaten durch Reduktion auf ein iteriertes Integral. Betrachten wir zunächst den Fall, dass der Pol O außerhalb des gegebenen Bereichs D liegt. Der Bereich D habe die Eigenschaft, dass jeder vom Pol ausgehende Strahl (die Koordinatenlinie y seine Grenze höchstens an zwei Punkten oder entlang eines ganzen Segments schneidet ( Abb. 17). Beachten Sie, dass die Extremwerte i des Polarwinkels die Grenzen der externen Integration sind. Der Strahl q> = geht durch den Punkt A der Kontur der Region D und der Strahl durch den Punkt B. Die Punkte Aw B teilen die Kontur der Region D in zwei Teile: ACB und AFB. Seien ihre Polargleichungen, wobei) einwertige stetige Funktionen sind, die die Bedingung erfüllen. Die Funktionen sind die Grenzen der internen Integration. Wenn wir zu iterierten Integralen übergehen, erhalten wir die folgende Formel. Insbesondere für die Fläche S der Domäne D für F(p, r 1 erhalten wir die Grenze der Region nur an einem Punkt oder entlang des gesamten Segments (Abb. 18) Sei - die Gleichung der Grenze der Region in Polarkoordinaten Dann Abb. 18 Beispiel Berechnen Sie das Integral, bei dem die Region ein Viertel des Einheitskreises im ersten Quadranten ist. Fahren wir mit den Polarkoordinaten fort. Dann ist der Integrationsbereich a Rechteck Das transformierte Integral / ist leicht zu berechnen: r Bemerkung: Wenn die Jacobi-Funktion im Bereich D ungleich Null ist, dann ist die Abbildung in einer Umgebung jedes Punktes dieses Bereichs eins zu eins, aber es kann vorkommen, dass die Die Abbildung des gesamten Bereichs ist nicht eins zu eins. Betrachten wir eine durch Funktionen definierte Abbildung. Der Jacobianwert dieser Funktionen ist gleich und daher überall ungleich Null. Trotzdem erhalten wir, also ist diese Zuordnung nicht eins zu eins. Wenn andererseits die Jacobi-Funktion einer Abbildung irgendwann verschwindet, kann es dennoch sein, dass die Abbildung in einer Umgebung dieses Punktes eineindeutig ist. Beispielsweise ist für eine durch Funktionen definierte Abbildung der Jacobi-Wert gleich Null und at, aber die Abbildung ist eineindeutig. Die umgekehrte Abbildung wird durch die Funktionen definiert

1.1 Definition des Doppelintegrals

1.2 Eigenschaften des Doppelintegrals

Die Eigenschaften des Doppelintegrals (und ihre Ableitung) ähneln den entsprechenden Eigenschaften des einfach definiten Integrals.

1°. Additivität. Wenn die Funktion f(x, y) im Bereich D integrierbar ist und wenn der Bereich D durch die Kurve Γ der Fläche Null in zwei verbundene Bereiche D 1 und D 2 ohne gemeinsame Innenpunkte geteilt wird, dann ist die Funktion f(x, y) ist in jedem der Bereiche D 1 und D 2 integrierbar, und

2°. Lineare Eigenschaft. Wenn die Funktionen f(x, y) und g(x, y) im Bereich D integrierbar sind, nicht wahr? Und? - irgendwelche reellen Zahlen, dann ist die Funktion [? f(x, y) + ? g(x, y)] ist auch im Bereich D integrierbar, und

3°. Wenn die Funktionen f(x, y) und g(x, y) im Definitionsbereich D integrierbar sind, dann ist das Produkt dieser Funktionen auch in D integrierbar.

4°. Wenn die Funktionen f(x, y) und g(x, y) beide im Bereich D und überall in diesem Bereich f(x, y) integrierbar sind? g(x, y), dann

5°. Wenn die Funktion f(x, y) im Definitionsbereich D integrierbar ist, dann ist die Funktion |f(x, y)| ist in die Domäne D integrierbar, und

(Natürlich impliziert die Integrierbarkeit von |f(x, y)| in D nicht die Integrierbarkeit von f(x, y) in D.)

6°. Der Mittelwertsatz. Wenn beide Funktionen f(x, y) und g(x, y) in einem Bereich D integrierbar sind, ist die Funktion g(x, y) überall in diesem Bereich nicht negativ (nicht positiv), M und m sind die beste Ober- und Untergrenze der Funktion f( x, y) im Bereich D, dann gibt es eine Zahl?, die die Ungleichung m erfüllt? ? ? M und so, dass die Formel

Insbesondere wenn die Funktion f(x, y) in D stetig ist und der Bereich D zusammenhängend ist, dann gibt es in diesem Bereich einen solchen Punkt (?, ?), was? = f(?, ?), und die Formel lautet

7°. Eine wichtige geometrische Eigenschaft. gleich der Fläche der Region D

Es sei ein Körper T im Raum gegeben (Abb. 2.1), der von unten durch die Region D und von oben durch den Graphen einer stetigen und nicht negativen Funktion begrenzt wird) z \u003d f (x, y,), der definiert ist im Bereich D, von den Seiten - durch eine zylindrische Oberfläche, deren Führung die Grenzdomäne D ist und deren Generatoren parallel zur Oz-Achse verlaufen. Einen solchen Körper nennt man Zylinderkörper.

1.3 Geometrische Interpretation des Doppelintegrals

1.4 Das Konzept eines Doppelintegrals für ein Rechteck

Sei eine beliebige Funktion f(x, y) überall auf dem Rechteck R = ? (Siehe Abb. 1).

Teilen wir das Segment a ? X? b in n Teilsegmente unter Verwendung der Punkte a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Diese Teilung durch Geraden parallel zu den Achsen Ox und Oy entspricht der Teilung des Rechtecks R in n · p Teilrechtecke R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Die angegebene Aufteilung des Rechtecks R wird mit dem Symbol T bezeichnet. Im Folgenden wird in diesem Abschnitt mit dem Begriff „Rechteck“ ein Rechteck bezeichnet, dessen Seiten parallel zu den Koordinatenachsen liegen.

Auf jedem Teilrechteck R kl wählen wir einen beliebigen Punkt (? k , ? l). Setzen wir?x k = x k - x k-1 , ?y l = y l - y l-1 , bezeichnen wir mit? R kl die Fläche des Rechtecks R kl . Offensichtlich ist ?R kl = ?x k ?y l .

heißt die Integralsumme der Funktion f(x, y), die einer gegebenen Partition T des Rechtecks R und einer gegebenen Auswahl von Zwischenpunkten (?k, ?l) auf den Teilrechtecken der Partition T entspricht.

Die Diagonale wird als Durchmesser des Rechtecks R kl bezeichnet. Ein Symbol? bezeichnen den größten der Durchmesser aller Teilrechtecke R kl .

Die Zahl I heißt Grenzwert der Integralsummen (1) für? > 0, wenn für eine positive Zahl? Können Sie eine solche positive Zahl angeben? Was wäre, wenn?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - Ich |< ?.

Eine Funktion f(x, y) heißt integrierbar (nach Riemann) auf einem Rechteck R, wenn es einen endlichen Grenzwert I der Integralsummen dieser Funktion gibt bei? > 0.

Dieser Grenzwert I heißt Doppelintegral der Funktion f(x, y) über dem Rechteck R und wird mit einem der folgenden Symbole bezeichnet:

Kommentar. Auf die gleiche Weise wie beim einmalig bestimmten Integral wird festgestellt, dass jede auf dem Rechteck R integrierbare Funktion f(x, y) auf diesem Rechteck beschränkt ist.

Dies gibt Anlass, im Folgenden nur beschränkte Funktionen f(x, y) zu betrachten.

Ein Problem, das zum Konzept eines Doppelintegrals führt.

Nehmen Sie an, dass eine Funktion von Teilen definiert ist und schreibe die Summe auf

welches man Integral nennt.

A: Unter einem bestimmten Integral (d.i.) der Funktion und der Wahl

Bezeichnung:

Zahlen heißen integrierbar (nach Riemann) auf .

T. Existenz: Vorausgesetzt, dass .

Gemäß der Definition von o.i. Beachten Sie, dass das Integral von der Form, den Grenzen und abhängt, jedoch nicht vom Symbol der anders ausgedrückten Variablenbezeichnung

Gemäß den Abschnitten 17.1.1 und 17.1.2 und der Definition von o.i. Wir schreiben die Formeln für die Fläche eines krummlinigen Trapezes: , Belegschaft

An :

Das Konzept der Doppelintegrale, Integralsummen.

Die Existenz eines Doppelintegrals, also der Grenze der Integralsumme für, scheint offensichtlich, da diese Grenze das Volumen eines zylindrischen Körpers angibt. Diese Argumentation ist jedoch nicht rigoros. In umfassenderen Kursen wird diese Behauptung rigoros bewiesen und als Doppelintegralexistenzsatz bezeichnet.

Der Existenzsatz. Für jede Funktion, die in einem begrenzten geschlossenen Bereich mit Fläche a stetig ist, gibt es ein Doppelintegral, d. h. es gibt eine Grenze von Integralsummen mit unbegrenzter Zunahme der Anzahl kleiner Flächen, vorausgesetzt, dass sich jede von ihnen auf einen Punkt zusammenzieht . Diese Grenze hängt weder von der Methode zur Aufteilung der Region in Teile noch von der Wahl der Punkte ab

Im Folgenden betrachten wir nur Funktionen, die im Integrationsbereich stetig sind.

Aus dem Existenzsatz folgt, dass wir beispielsweise den Bereich a in kleine Rechtecke mit geraden Seiten parallel zu den Koordinatenachsen unterteilen können (Abb. 230). Dabei. Wenn wir dann in jedem kleinen Rechteck einen Punkt auswählen, können wir gemäß der Definition des Doppelintegrals schreiben

Um hervorzuheben, dass das Doppelintegral als Grenzwert einer Summe der Form erhalten werden kann, wird anstelle der Notation auch die Notation verwendet

Der Ausdruck wird als Flächenelement in kartesischen Koordinaten bezeichnet und entspricht der Fläche eines Rechtecks, dessen Seiten parallel zu den Koordinatenachsen liegen.

Beachten Sie, dass bei der Bildung der Integralsumme die an die Grenze des Bereichs a angrenzenden Flächen nicht die Form von Rechtecken haben. Es kann jedoch nachgewiesen werden, dass der Fehler beim Ersetzen solcher Flächen durch Rechtecke mit Flächen im Grenzwert auf Null reduziert wird.

Eigenschaften von Doppelintegralen

Die Eigenschaften des Doppelintegrals (und ihre Ableitung) ähneln den entsprechenden Eigenschaften des einfach definiten Integrals.

3°. Wenn funktioniert F(X, j) Und G(X, j) sind in die Domäne integrierbar D, dann ist das Produkt dieser Funktionen auch in integrierbar D.

4°. Wenn funktioniert F(X, j) Und G(X, j) sind beide in die Domäne integrierbar D und überall in dieser Gegend F(X, j) ≤ G(X, j), Das

5°. Wenn die Funktion F(X, j) ist in die Domäne integrierbar D, dann ist die Funktion | F(X, j)| in die Umgebung integrierbar D, Und

(Natürlich aus der Integrierbarkeit | F(X, j)| V D Integrierbarkeit folgt nicht F(X, j) V D.)

Insbesondere wenn die Funktion F(X, j) ist stetig in D, und die Gegend D in Verbindung gebracht, dann gibt es in diesem Bereich einen solchen Punkt ( ξ , η ), Was μ = F(ξ , η ) und Formel (11) nimmt die Form an

Für eine Funktion aus zwei Variablen, definiert als z = F(X, j) .

Das Doppelintegral wird wie folgt geschrieben:

Hier D- eine durch Linien begrenzte flache Figur, deren Ausdrücke (Gleichheiten) in der Aufgabe zur Berechnung des Doppelintegrals angegeben sind. Links und rechts sind Gleichheiten, bei denen die Variable links ist X, und oben und unten - durch Gleichheiten, in denen die Variable links steht j. Dieser Ort und darüber hinaus ist einer der wichtigsten für das Verständnis der Technik der Berechnung des Doppelintegrals.

Berechnen Sie das Doppelintegral - bedeutet, eine Zahl zu finden, die der Fläche der genannten Figur entspricht D .

Bis wir uns berühren Definitionen des Doppelintegrals , und wir werden lernen, es zu berechnen. Es ist einfacher zu verstehen, was ein Doppelintegral ist, wenn mehrere Probleme zu seiner Berechnung gelöst wurden. Die Definition eines Doppelintegrals finden Sie daher am Ende dieser Lektion. Wenn wir ein wenig nach vorne blicken, können wir nur feststellen, dass die Definition des Doppelintegrals auch mit der genannten Figur verbunden ist D .

Wenn die Figur D ist ein Rechteck, alle Linien, die es begrenzen, sind Geraden. Wenn die Figur D- krummlinig, dann wird es links und rechts durch gerade Linien und von oben und unten durch gekrümmte Linien begrenzt, die durch die in der Aufgabe angegebenen Gleichheiten gegeben sind. Es gibt auch Fälle, in denen eine Figur D- ein Dreieck, aber über solche Fälle etwas weiter.

Um das Doppelintegral zu berechnen, ist es daher notwendig, die an die Figur angrenzenden Linien zu sortieren D, das einen strengen Namen hat – die Region der Integration. Sortieren Sie nach links und rechts sowie oben und unten. Dies wird erforderlich sein, wenn Reduktion des Doppelintegrals auf das iterierte Integral – die Methode zur Berechnung des Doppelintegrals.

Fall mit rechteckiger Fläche:

Fall einer krummlinigen Region:

Und dies ist bereits eine Lösung der uns bekannten bestimmten Integrale, in denen die Ober- und Untergrenzen der Integration festgelegt sind. Ausdrücke, die Linien definieren, die eine Form begrenzen D, werden die Grenzen der Integration für die üblichen bestimmten Integrale sein, denen wir uns bereits nähern.

Reduktion des Doppelintegrals auf iteriert

Rechteckiges Gehäuse

Eine solche Funktion soll ein Doppelintegral haben

Zu Berechnen Sie dieses Doppelintegral , müssen Sie es auf das iterierte Integral reduzieren, das die Form hat

Zuerst müssen Sie das innere (rechte) bestimmte Integral berechnen, dann das äußere (linke) bestimmte Integral.

Sie können die Rollen wechseln X Und j

Beispiel 1 Berechnen Sie das Doppelintegral

Wir berechnen das innere (rechte) Integral und betrachten y als Konstante. Wir erhalten.

Beispiel 2 Berechnen Sie das Doppelintegral

Lösung. Wir reduzieren dieses Doppelintegral auf das iterierte Integral

Auf der Zeichnung bauen wir den Integrationsbereich auf:

Nun berechnen wir das äußere (linke) Integral aus dem gerade berechneten inneren (rechten) Integral:

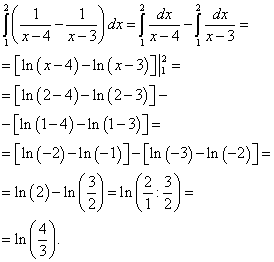
Das Ergebnis wird die Lösung dieses Doppelintegrals sein.

Berechnen Sie das Doppelintegral selbst und sehen Sie sich dann die Lösung an

Fall einer krummlinigen oder dreieckigen Region

Gegeben sei erneut eine Funktion zweier Variablen F(X, j) , und die Einschränkungen für D: sieht etwas anders aus:

Dieser Eintrag bedeutet, dass die Zahl D Grenze links und rechts, wie im Fall einer geradlinigen Region - gerade Linien X = A Und X = B, aber unten und oben sind die Kurven, die durch die Gleichungen und gegeben sind. Mit anderen Worten, und sind Funktionen.

Eine solche Funktion soll auch ein Doppelintegral haben

Um dieses Doppelintegral zu berechnen, müssen wir es auf das iterierte Integral reduzieren, das die Form hat

Hier liegen die Grenzen der Integration A Und B sind Zahlen und und sind Funktionen. Bei einem Dreiecksbereich ist eine der Funktionen oder die Gleichung einer Geraden. Dieser Fall wird in Beispiel 3 besprochen.

Wie im Fall einer geradlinigen Region müssen Sie zuerst das rechte bestimmte Integral und dann das linke bestimmte Integral berechnen.

Auf die gleiche Weise können Sie auch die Rollen wechseln. X Und j. Dann hat das iterierte Integral die Form

Ein solches iteriertes Integral muss auf genau die gleiche Weise gelöst werden: Zuerst das innere (rechte) Integral, dann das äußere (linke).

Beispiel 5 Berechnen Sie das Doppelintegral

Lösung. Wir reduzieren dieses Doppelintegral auf das iterierte Integral

Auf der Zeichnung bauen wir den Integrationsbereich auf und sehen, dass er dreieckig ist:

Wir berechnen das innere (rechte) Integral und betrachten x als Konstante. Wir erhalten.

Nun berechnen wir das äußere (linke) Integral des gerade berechneten inneren (rechten) Integrals. Zunächst stellen wir dieses Integral als Summe von Integralen dar:

Wir berechnen den ersten Term:

Wir berechnen den zweiten Term:

Wir berechnen den dritten Term:

Wir erhalten die Summe, die die Lösung dieses Doppelintegrals sein wird:

Beispiel 6 Berechnen Sie das Doppelintegral

Lösung. Wir reduzieren dieses Doppelintegral auf das iterierte Integral

Auf der Zeichnung bauen wir den Integrationsbereich auf:

Wir berechnen das innere (rechte) Integral und betrachten x als Konstante. Wir erhalten.

Nun berechnen wir das äußere (linke) Integral aus dem gerade berechneten inneren (rechten) Integral:

Das Ergebnis wird die Lösung dieses Doppelintegrals sein.

X- richtig und falsch j-richtige und falsche Integrationsbereiche

Es kommt vor, dass der Integrationsbereich eines Doppelintegrals durch solche Linien begrenzt ist, dass es notwendig wird, den Integrationsbereich in Teile aufzuteilen und jedes entsprechende iterierte Integral separat zu lösen. Dies sind die Fälle, wenn:

1) Der Integrationsbereich ist eine Figur, die zwei oder mehr gerade oder gekrümmte Linien in Form einer unteren oder oberen (linken oder rechten) Grenze aufweist;

2) Der Integrationsbereich ist eine Figur, deren Grenze die Linien an mehr als zwei Punkten schneiden.

Wenn das oben Gesagte für die linke oder rechte Grenze des Integrationsbereichs gilt, werden die durch die Linien ausgedrückten Einschränkungen durch ausgedrückt X, dann heißt der Integrationsbereich X- falsch. Wenn eine gerade Linie j = j0 schneidet die entsprechende Grenze nur in einem Punkt, und wenn nur eine Linie oder Kurve als Grenze dient, wird das Integrationsgebiet genannt X-richtig

Ebenso, wenn die Grenze durch Linien definiert wird, ausgedrückt in Form von j, gerade X = X0 sich in mehr als einem Punkt schneidet, oder wenn mehr als eine Linie oder Kurve als Grenze dient, dann wird der Integrationsbereich genannt j- falsch. Bringen Sie jetzt die Schilder hervor j-der richtige Bereich, vermutlich ganz einfach.

Bisher haben wir Beispiele betrachtet X- falsch und j-Regelmäßige Integrationsbereiche. Betrachten Sie nun die Fälle, in denen die Korrektheitsbedingung verletzt wird.

Beispiel 7 Berechnen Sie ein Doppelintegral, dessen Integrationsbereich durch Linien begrenzt ist j = X , xy = 1 , j = 2 .

Lösung. Der Integrationsbereich ist j-falsch, da der untere Rand nicht mit einer einzigen Zeile festgelegt werden kann j = j(X) . Wie Sie in der Abbildung oben sehen können, besteht die Untergrenze aus j = X(dunkles Kastanienbraun) und xy= 1 (grün). Daher direkt X= 1 (schwarz) können wir den Integrationsbereich in zwei Teile teilen - und .

Dieses Doppelintegral berechnet sich wie folgt:

Änderung der Integrationsreihenfolge

Wie oben erwähnt, kann man nach der Reduzierung des Doppelintegrals auf das iterierte Integral die Variablen ändern X Und j Rollen, oder mit anderen Worten, die Reihenfolge der Integration ändern.

Die Änderung der Integrationsreihenfolge kann bildlich durch die folgenden Worte von O „Henry“ beschrieben werden: „So verhält sich der Bewohner des Dschungels – das Biest, das in den Käfig gelangt ist, und so verhält sich der Bewohner des Käfigs.“ – der Mann, verloren im Dschungel der Zweifel.“ Das Ergebnis ist, auch laut O „Henry, ein und dasselbe: „Chalmers riss den Brief in tausend kleine Stücke und begann, seinen teuren Teppich zu quälen, indem er ihn hin und her bewegte hervor. ( O. Henry. Scheherazade vom Madison Square.)

Dann haben wir das Linksintegral über der Variablen X, und zwar das Richtige j, dann wird nach einer Änderung der Integrationsreihenfolge alles umgekehrt sein. Dann müssen die Integrationsgrenzen für das „neue“ y vom „alten“ x „entlehnt“ werden und die Integrationsgrenzen für das „neue“ x sollten in der Form erhalten werden Umkehrfunktion, Lösen der Gleichung in Bezug auf x, die den Grenzwert für y festlegt.

Beispiel 8

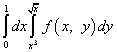Lösung. Nach Änderung der Integrationsreihenfolge wird das Integral über y links und das Integral über x rechts. Wir werden die Integrationsgrenzen für den „neuen“ Spieler vom „alten“ X übernehmen, das heißt, die untere Grenze ist gleich Null und die obere Grenze ist gleich eins. Die Integrationsgrenzen für den „alten“ Spieler sind durch die Gleichungen und gegeben. Nachdem wir diese Gleichungen nach x gelöst haben, erhalten wir neue Integrationsgrenzen für x:

(unten) und (oben).

Nach Änderung der Integrationsreihenfolge wird das iterierte Integral also wie folgt geschrieben:

Nach einer Änderung der Integrationsreihenfolge im Doppelintegral wird der Integrationsbereich häufig zu j- falsch oder X- falsch (siehe vorheriger Absatz). Dann ist es erforderlich, den Integrationsbereich in Teile aufzuteilen und jedes entsprechende iterierte Integral separat zu lösen.

Da die Aufteilung des Integrationsbereichs in Teile für viele Studierende gewisse Schwierigkeiten bereitet, beschränken wir uns nicht auf das im vorherigen Absatz gegebene Beispiel, sondern analysieren noch ein paar weitere Beispiele.

Beispiel 9Ändern Sie die Integrationsreihenfolge für das iterierte Integral

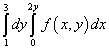Lösung. Der Integrationsbereich dieses iterierten Integrals wird also durch die Geraden begrenzt j = 1 , j = 3 , X = 0 , X = 2j .

Bei der Integration in einer anderen Reihenfolge besteht die untere Grenze der Region aus zwei Geraden: AB Und Chr, die durch die Gleichungen gegeben sind j= 1 und j = X/2 , was in der Abbildung unten zu sehen ist.

Der Ausweg aus dieser Unsicherheit besteht darin, den Integrationsbereich in zwei Teile aufzuspalten. Der Integrationsbereich wird durch eine gerade Linie geteilt BM. Neue Integrationsgrenzen werden durch Finden der Umkehrfunktion berechnet. Gemäß dieser Lösung ist das iterierte Integral nach Änderung der Integrationsreihenfolge gleich der Summe zweier Integrale:

Natürlich wird die Lösung des Doppelintegrals dieselbe sein, die sich auf das in der Bedingung dieses Beispiels angegebene iterierte Integral reduziert.

Beispiel 10Ändern Sie die Integrationsreihenfolge für das iterierte Integral

Lösung. Der Integrationsbereich des iterierten Integrals wird also durch die Geraden begrenzt X = 0 , X= 2 und Kurven und .

Wie in der Abbildung unten zu sehen ist, eine gerade Linie parallel zur Achse 0x, schneidet die untere Grenze des Integrationsbereichs an mehr als zwei Punkten.

Daher teilen wir das Integrationsgebiet durch gerade Linien, die in der Abbildung schwarz eingezeichnet sind, in drei Teile. Neue Integrationsgrenzen werden durch Finden der Umkehrfunktion berechnet. Die Grenzen für die drei neuen Integrationsbereiche werden wie folgt sein.

Gemäß dieser Lösung ist das wiederholte Integral nach Änderung der Integrationsreihenfolge gleich der Summe von drei Integralen:

Die gleiche Summe von drei Integralen entspricht dem Doppelintegral, das sich auf das in der Bedingung dieses Beispiels angegebene iterierte Integral reduziert.

Und doch behindern Umstände höherer Gewalt die Studierenden oft schon beim vorherigen Schritt – der Festlegung der Grenzen der Integration. Ängste und Verwirrung sind nicht unbegründet: Wenn es normalerweise ausreicht, sich die Zeichnung anzusehen, um den Integrationsbereich in Teile zu zerlegen und das iterierte Integral – die Tabelle der Integrale – zu lösen, dann ist etwas Übungserfahrung im Festlegen der Grenzen erforderlich Integration. Lassen Sie uns ein Beispiel durchgehen, in dem wir uns nur auf die Anordnung der Integrationsgrenzen und – fast automatisch – auf die Aufteilung der Region konzentrieren und die Lösung selbst weglassen.

Beispiel 11. Finden Sie die Integrationsgrenzen eines Doppelintegrals im Integrationsbereich D wie folgt einstellen:

j - 2X ≤ 0;
2 Jahre - X ≥ 0;
xy ≤ 2.

Lösung. explizit (via X Und j„ohne Verunreinigungen“) sind die den Integrationsbereich begrenzenden Linien nicht angegeben. Da es sich bei x am häufigsten um gerade Linien handelt, die an einem Punkt die durch y ausgedrückten oberen und unteren Grenzen berühren, gehen wir genau diesen Weg. Darüber hinaus erhalten wir bei einer Änderung der Integrationsreihenfolge einen Integrationsbereich mit derselben Fläche. Lösen wir die Ungleichungen für den Spieler und erhalten:

j ≤ 2X;
j ≥ X/2;
j ≤ 2/X.

Die resultierenden Linien bauen wir auf der Zeichnung auf. Die Integrationsgrenzen bezüglich x sind tatsächlich die Geraden X= 0 und X= 2 . Es stellte sich jedoch heraus, dass es sich um eine Integrationsregion handelte j-falsch, da der obere Rand nicht mit einer Zeile festgelegt werden kann j = j(X) .

Es könnte nützlich sein zu lesen: