Вершины трапеции. Материал по геометрии на тему "трапеция и ее свойства". Свойства равнобедренной трапеции
Г.И. Ковалева
МЕТОДИКА ИЗУЧЕНИЯ СВОЙСТВ ТРАПЕЦИИ
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует от учащихся знаний «непрограммных» свойств трапеции. (Программными считаются свойство средней линии трапеции, свойства диагоналей и углов равнобедренной трапеции.) Какими же замечательными свойствами обладает трапеция? Где и когда их изучать в школьном курсе геометрии?
Методика изучения свойств трапеции
Теперь, когда мы видели несколько типов, давайте узнаем о фигурах, которые не обладают свойствами параллелограммов. Напомним, что параллелограммы представляют собой четырехугольники, противоположные стороны которых параллельны. В этом разделе мы рассмотрим четырехугольники, противоположные стороны которых могут пересекаться в некоторой точке. Давайте начнем наше исследование, изучив некоторые свойства трапеций. Определение. Трапеция представляет собой четырехугольник с ровно одной парой параллельных сторон.
После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Отрабатывая основной прием
решения задач на трапецию «провести
две высоты», учащимся необходимо
предложить задачу: «Пусть BT
– высота равнобедренной трапеции ABCD
с основаниями BC
и AD
.
 ,
,
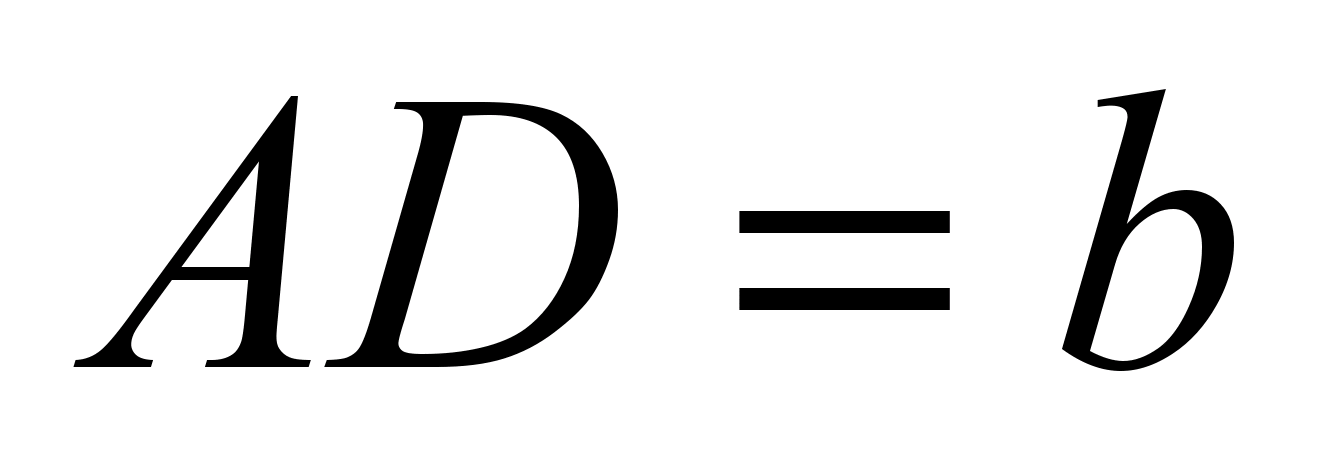 .
Найдите длины отрезков AT
и TD
».
.
Найдите длины отрезков AT
и TD
».
«Использование тригонометрии при решении планиметрических задач»
Поскольку трапеция должна иметь ровно одну пару параллельных сторон, нам нужно будет доказать, что одна пара противоположных сторон параллельна, а другая - не в нашей. Если мы забудем доказать, что одна пара противоположных сторон не параллельна, мы не исключаем возможность того, что четырехугольник является параллелограммом. Поэтому этот шаг будет абсолютно необходим, когда мы будем работать над различными упражнениями, включающими трапеции.
Прежде чем мы погрузимся прямо в наше исследование трапецоидов, необходимо будет узнать имена разных частей этих четырехугольников, чтобы быть конкретными относительно его сторон и углов. Все трапеции содержат две основные части: основания и ноги. Противоположные стороны трапеции, параллельные друг другу, называются основаниями. Остальные стороны трапеции, которые пересекаются в какой-то точке, если они расширены, называются ногами трапеции.
Тема «Подобие фигур» очень благодатна для изучения свойств трапеции. Например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Назовем это утверждение с войством треугольников, на которые разбивается трапеция ее диагоналями. Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Вторую часть можно предложить учащимся в виде задачи.
Подобие образованных треугольников трапеции
Верхняя и нижняя стороны трапеции проходят параллельно друг другу, поэтому они являются основаниями трапеции. Другие стороны трапеции пересекаются, если они расширены, поэтому они являются ногами трапеции. Сегмент, который соединяет середины ног трапеции, называется средним. Длина этого сегмента всегда равна половине суммы трапециевидных оснований или.
Отношение длин отрезков и оснований
Измерение среднего сегмента зависит только от длины трапециевидных оснований. Однако существует важная характеристика, что некоторые трапеции имеют исключительно зависимость от ее ног. Давайте посмотрим на эти трапеции сейчас. Равнобедренная трапеция - трапеция, ноги которой конгруэнтны. По определению, если четырехугольник имеет ровно одну пару параллельных линий, то четырехугольник является трапецией. Определение равнобедренной трапеции добавляет другую спецификацию: ноги трапеции должны быть конгруэнтными.
Аналогично, треугольники
BOC
и АОВ
имеют
общую высоту, если принять за их основания
отрезки CO
и OA
.
Тогда
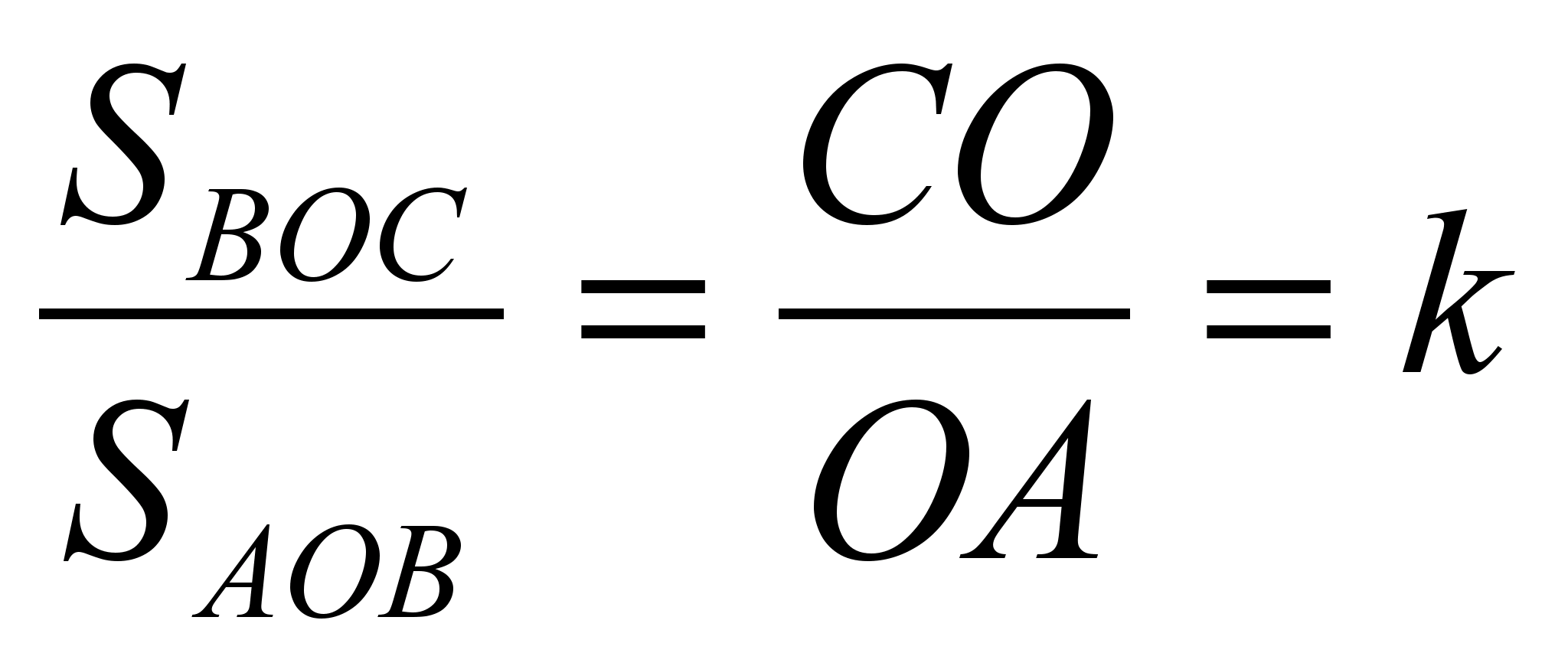 и
и
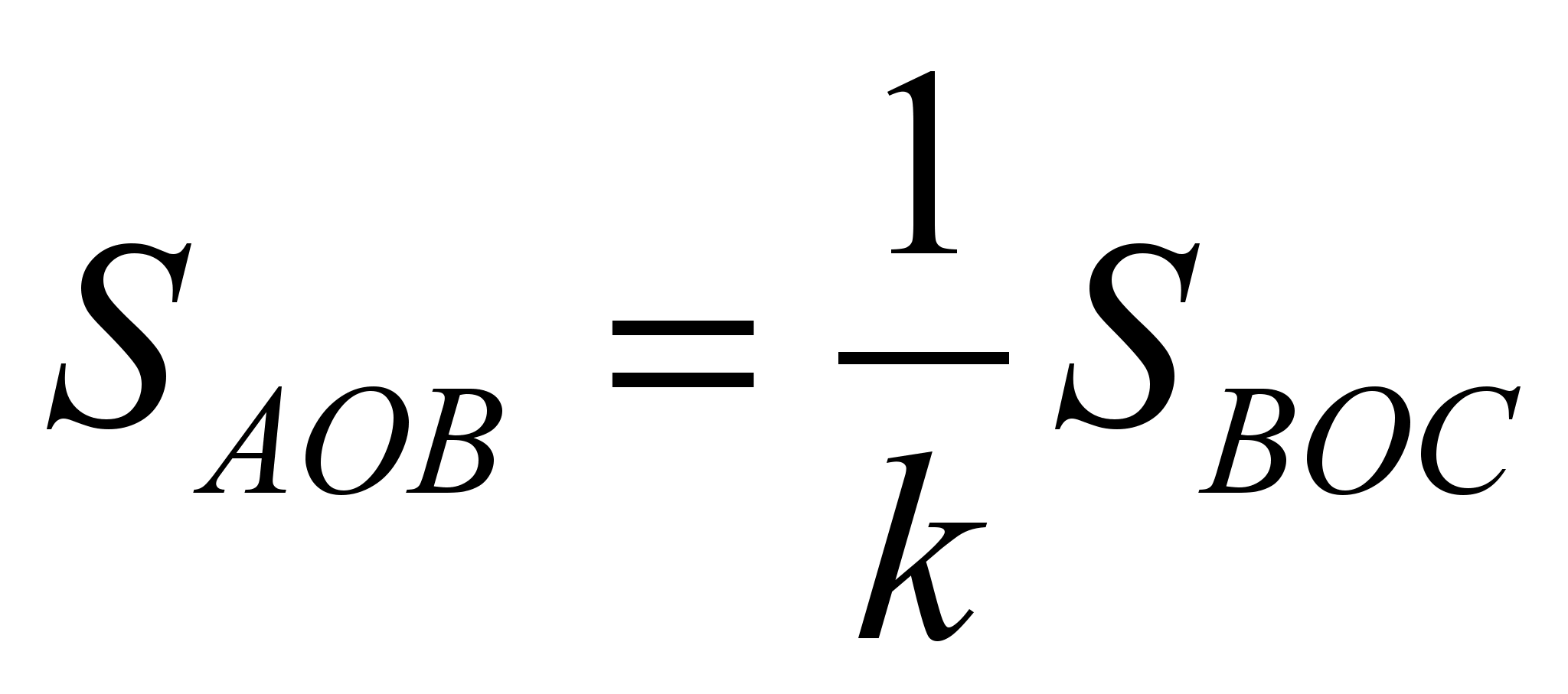 .
.
Из этих двух предложений следует,
что
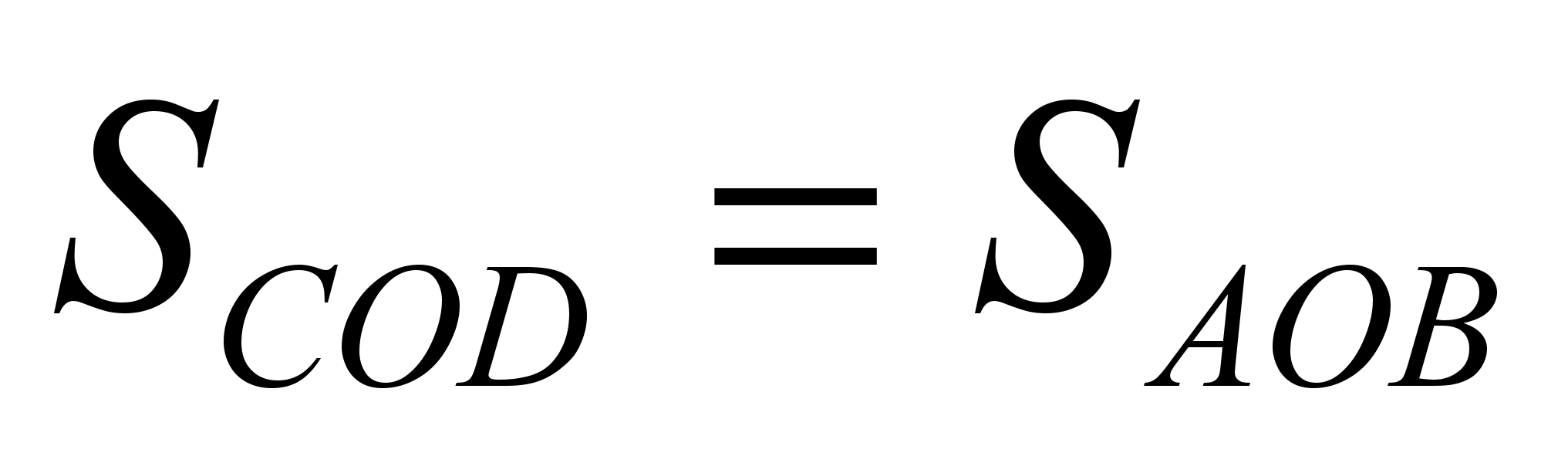 .
.
Есть несколько теорем, которые мы можем использовать, чтобы помочь нам доказать, что трапеция является равнобедренной. Эти свойства перечислены ниже. Трапеция равнобедренная тогда и только тогда, когда базовые углы конгруэнтны. Трапеция является равнобедренной, если и только если диагонали конгруэнтны.
Если трапеция является равнобедренной, то ее противоположные углы являются дополнительными. Кайт представляет собой четырехугольник с двумя различными парами смежных сторон, которые являются конгруэнтными. Напомним, что параллелограммы также имели пары конгруэнтных сторон. Однако их конгруэнтные стороны всегда были противоположными. У змеев есть две пары конгруэнтных сторон, которые встречаются в двух разных точках. Давайте посмотрим на приведенную ниже иллюстрацию, чтобы помочь нам понять, как выглядит змей.
Было бы замечательно не
останавливаться на сформулированном
утверждении, а найти связь
между площадями треугольников, на
которые разбивается трапеция ее
диагоналями
, предложив
учащимся решить задачу: «Пусть O
– точка пересечения диагоналей трапеции
ABCD
с основаниями BC
и AD
.
Известно, что площади треугольников
BOC
и AOD
равны соответственно
 и
и
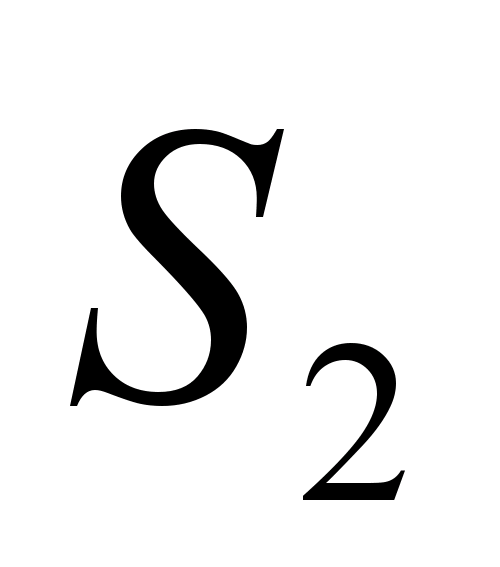 .
Найдите площадь трапеции».
.
Найдите площадь трапеции».
У кайтов есть несколько свойств, которые помогут нам идентифицировать их из других четырехсторонних. Диагонали кайта встречаются под прямым углом. У кайтов есть ровно одна пара противоположных углов, которые являются конгруэнтными. Эти два свойства проиллюстрированы на диаграмме ниже.
Это наша единственная пара конгруэнтных углов, потому что? Позвольте практике делать некоторые проблемы, которые требуют использования свойств трапеций и воздушных змеев, о которых мы только что узнали. Поскольку нам даны длины оснований трапеции, мы можем выяснить, какова должна быть длина среднего сегмента. Давайте используем формулу, которую мы дали для среднего сегмента, чтобы понять это.
Так как
.
Отсюда
,
из подобия треугольников B
О
C
и AOD
следует, что
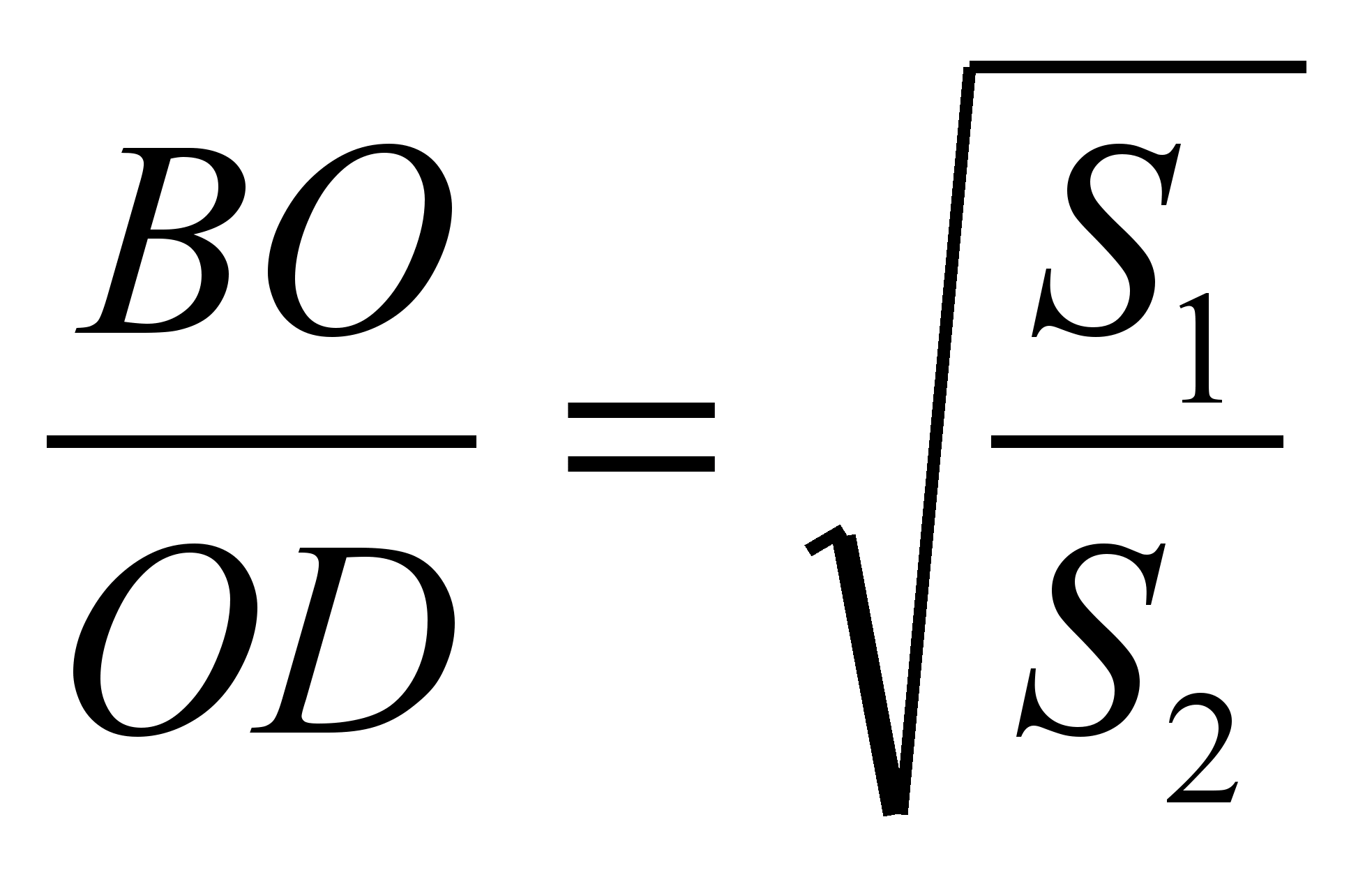 .Следовательно,
.Следовательно,
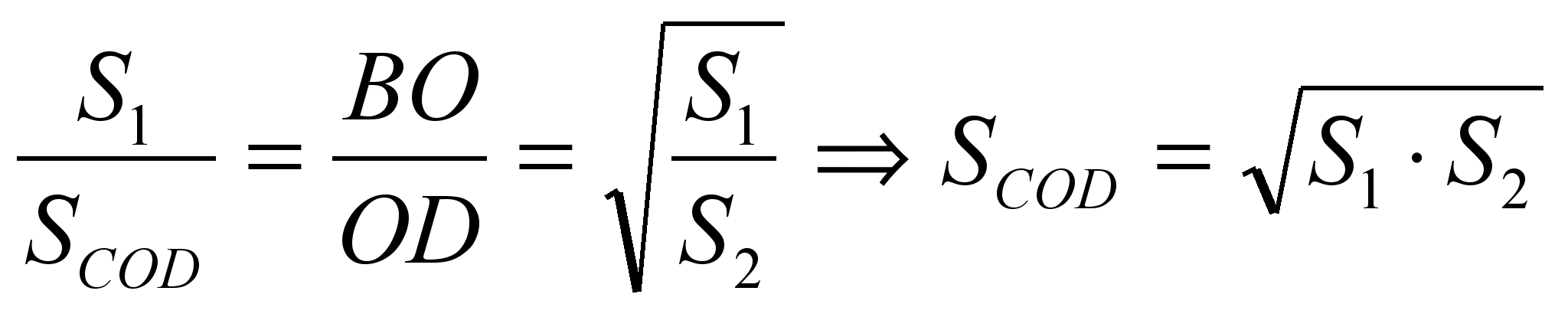 .
Тогда
.
Тогда
С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. Предлагаем учащимся решить задачу: «Пусть O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD . , . Найдите длину отрезка PK , проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О ».
На рисунке нам была дана только мера одного угла, поэтому мы должны иметь возможность выводить больше информации на основе этого одного элемента. Поскольку четырехугольник является равнобедренной трапецией, мы знаем, что базовые углы конгруэнтны. Теперь, давайте выясним, какая сумма?
Вместе они имеют в общей сложности 128 °. Напомним теорему о внутренних углах многоугольника, что внутренние углы четырёхугольника должны быть 360 °. Итак, давайте попробуем использовать это таким образом, чтобы помочь нам определить меру? Сначала давайте подытожим все углы и установите его равным 360 °.
Отсюда
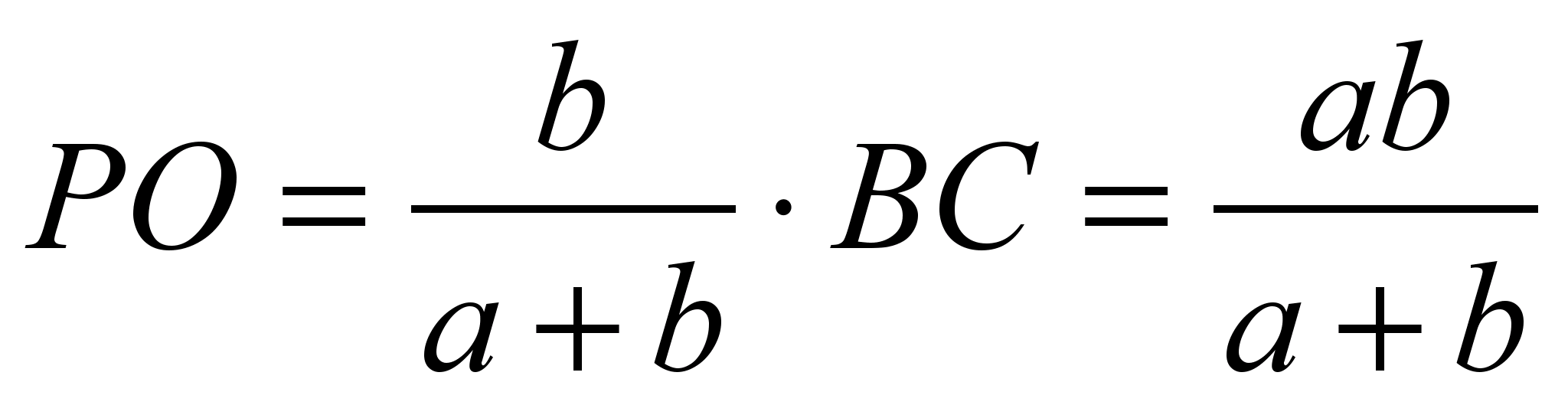 .
.
Аналогично, из подобия треугольников
DOK
и DBC
,
следует, что
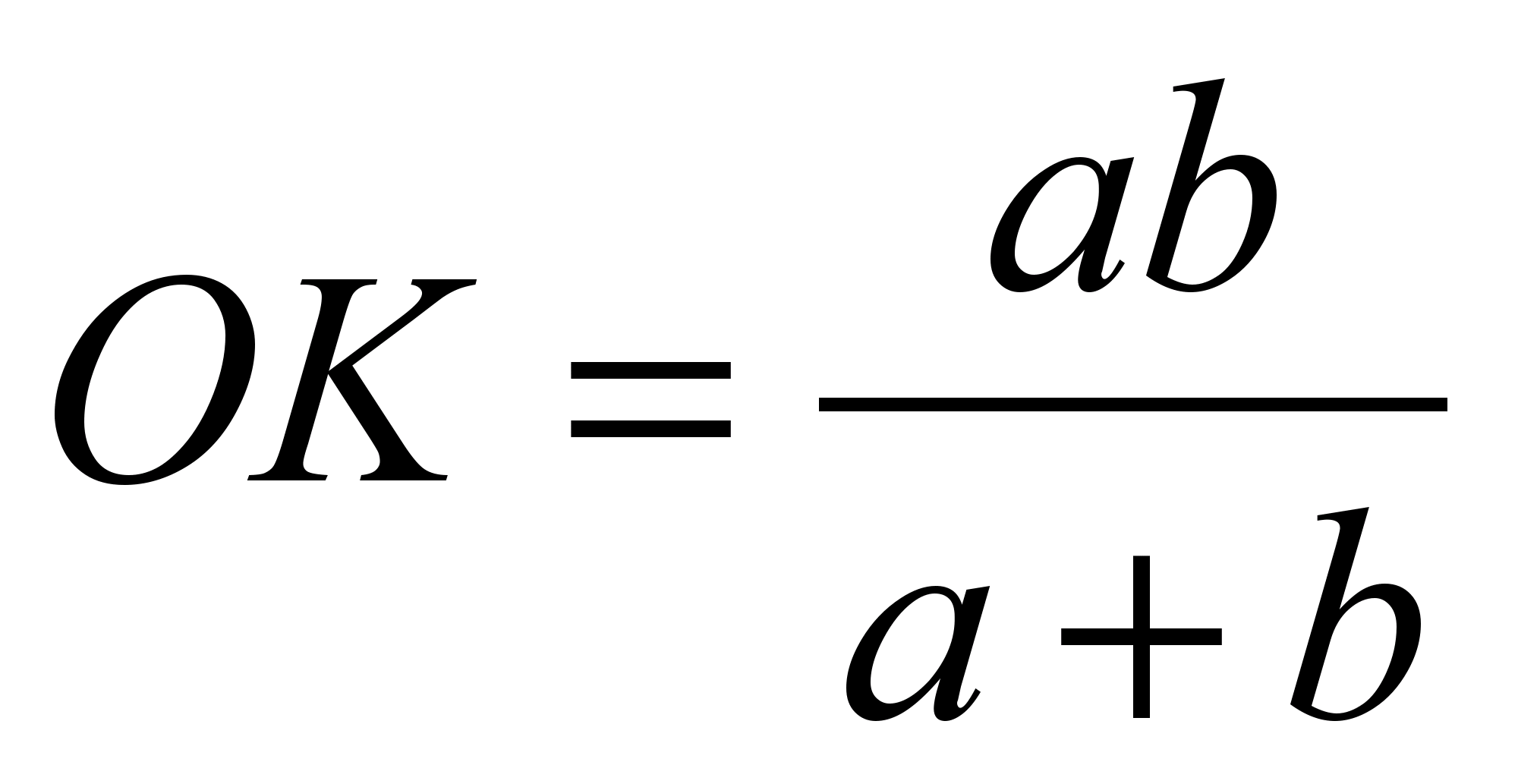 .
Отсюда
.
Отсюда
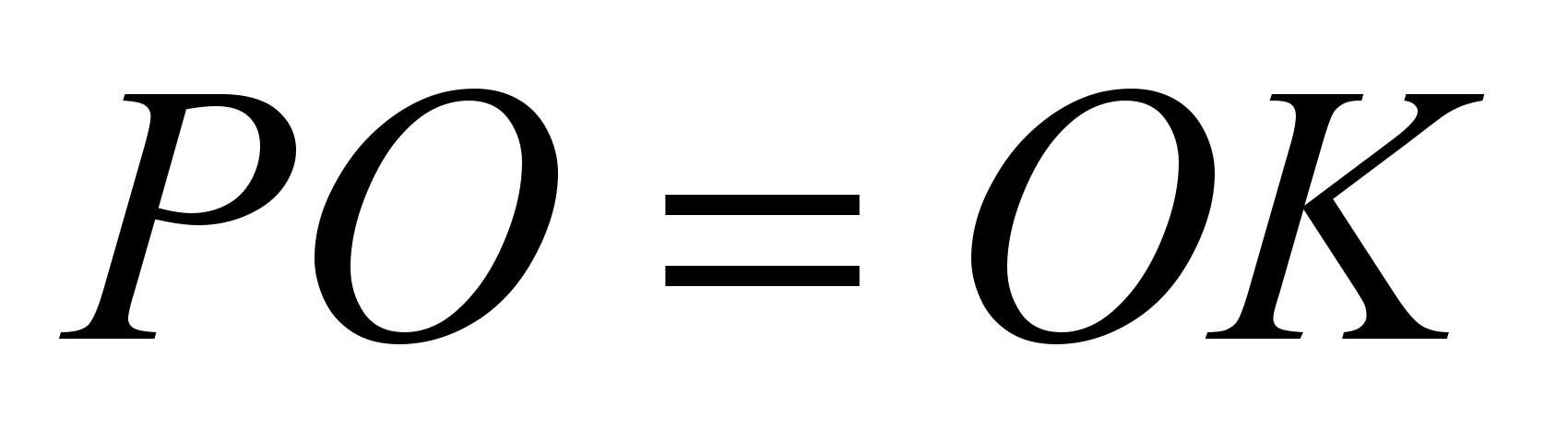 и
и
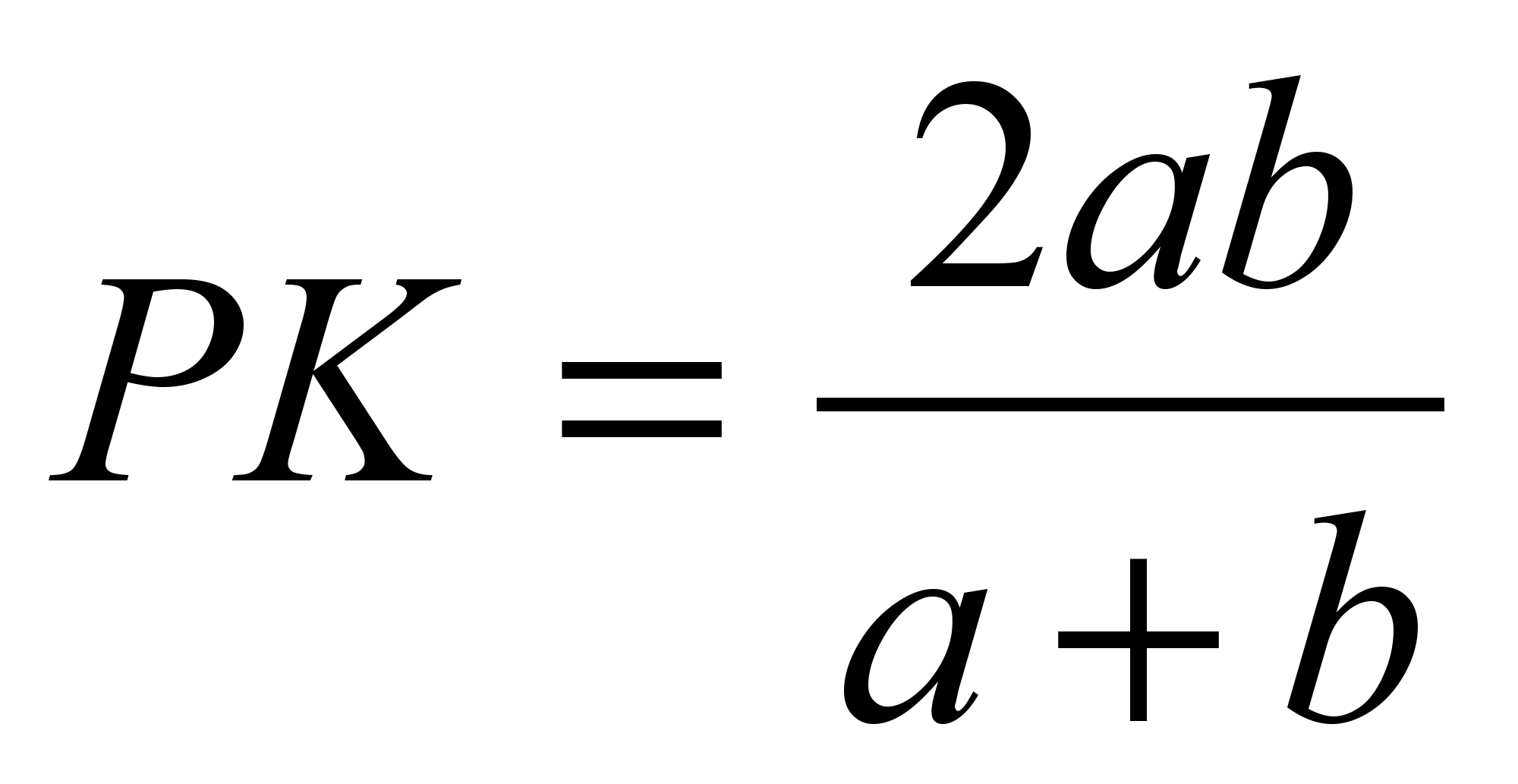 .
.
Описанная около трапеции окружность
Таким образом, если мы определяем меры? Это значение означает, что мера? Наконец, мы можем установить 116, равное выражению, показанному в? Хотя вышеописанный метод был глубоким способом решения упражнения, мы могли бы просто использовать свойство, что дополнительные углы равнобедренных трапеций являются дополнительными. Решение таким образом происходит намного быстрее, так как нам нужно только найти, что такое дополнение с углом 64 °.
Как только мы дойдем до этой точки в нашей проблеме, мы просто установим 116 равным 4 и решим, как и раньше. Нам также было дано это? В прошлом мы изучили несколько теорем конгруэнции треугольника, которые могут быть применимы в этой ситуации, если мы можем просто найти другую сторону или угол, которые являются конгруэнтными.
Добиваемся от учащихся осознания доказанного свойства: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.
Следующее свойство четырех точек: в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.
Наша новая иллюстрация показана ниже. Ниже приведено двухстоечное геометрическое доказательство этого упражнения. Чтобы получить доступ к таким геометриям, как. Перестаньте бороться и начинайте учиться сегодня с тысяч бесплатных ресурсов! Свойства представлены ссылками на соответствующие уроки. Уроки перечислены в логическом порядке, а это означает, что каждый урок относится к предыдущим. и не ссылается на это. Список объединяет соответствующие уроки, которые расположены на разных страницах этого сайта.
Диагонали и высота трапеции
Трапеция является равнобедренной, если и только если ее базовые углы конгруэнтны. Трапеция является равнобедренной, если и только если ее две диагонали конгруэнтны. Средняя линия трапеции параллельна ее основаниям. Длина средней линии трапеции составляет половину суммы длин ее оснований. В трапеции участок линии, оттянутый от середины боковой стороны, параллельной основаниям, пересекает другую боковую сторону в ее средней точке.
Знакомя учащихся с подобием фигур (не треугольников), можно предложить найти длину отрезка разбивающего трапецию на две подобных.
Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.
После вывода формулы площади трапеции полезно доказать свойство отрезка, делящего трапецию на две равновеликие.
Средняя линия трапеции - это локус точек, равноудаленных от двух прямых, содержащих основы трапеции. В трапеции сумма внутренних углов на концах боковой стороны равна 180 °. В трапеции средняя линия делит пополам любой отрезок прямой, соединяющий точку на более коротком основании с точкой на большем основании. В трапеции расстояние между серединами его диагоналей составляет половину разницы длин более крупных и более коротких оснований.
Если в трапеции сумма двух противоположных внутренних углов равна 180 °, то трапеция является равнобедренной. В равнобедренной трапеции прямая, проходящая через диагональное пересечение, параллельное основаниям, делит пополам угол между диагоналями. В равнобедренной трапеции боковая сторона видна под одним углом от любой из двух противоположных вершин.
Составим систему
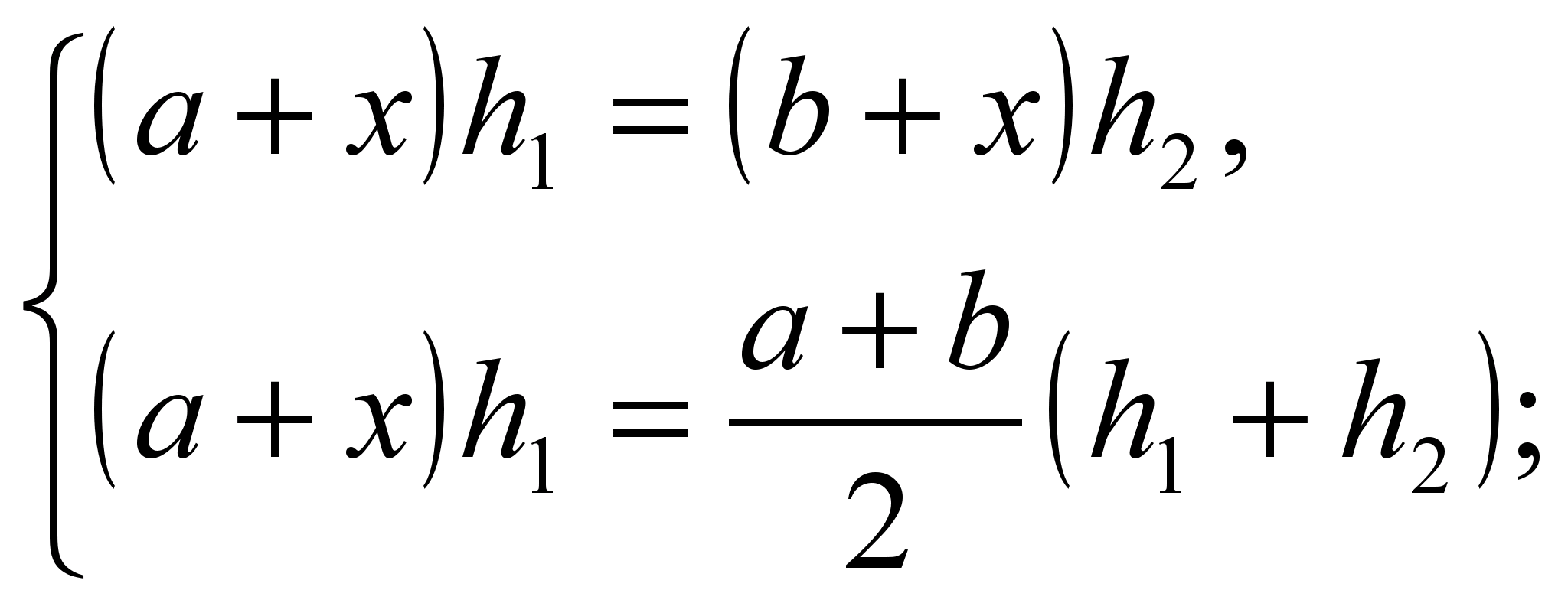
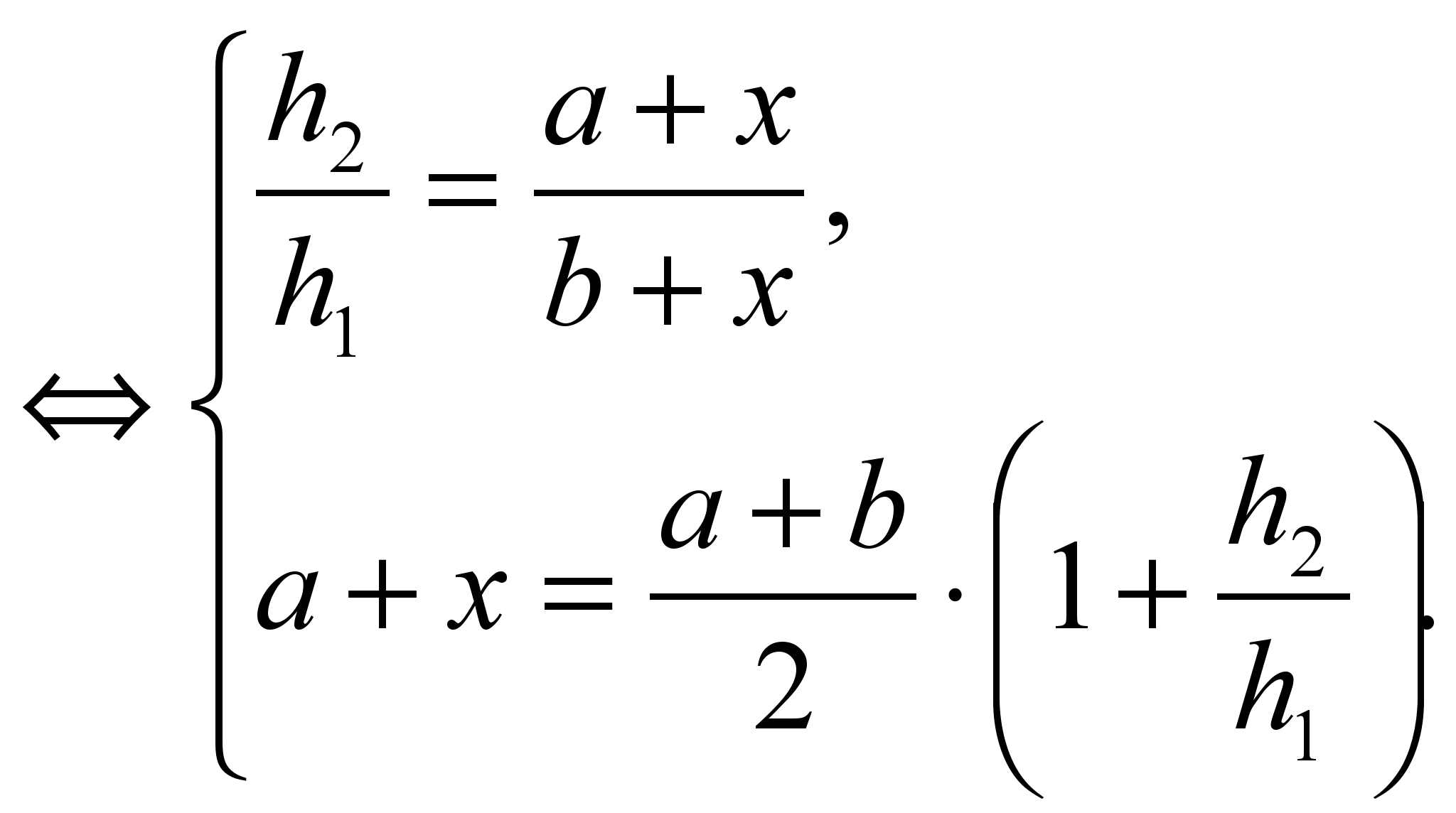
Решение системы
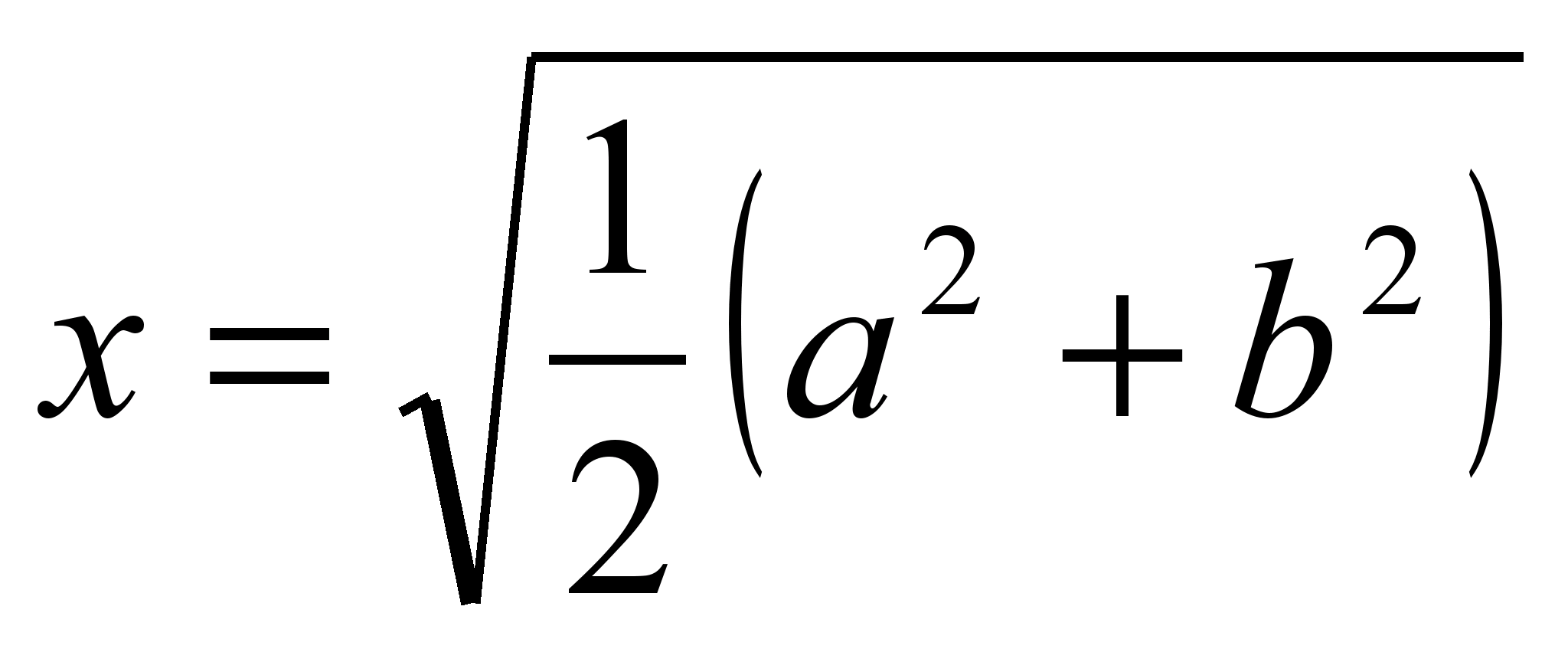 .
.
Таким образом, длина
отрезка, делящего трапецию на две
равновеликие, равна
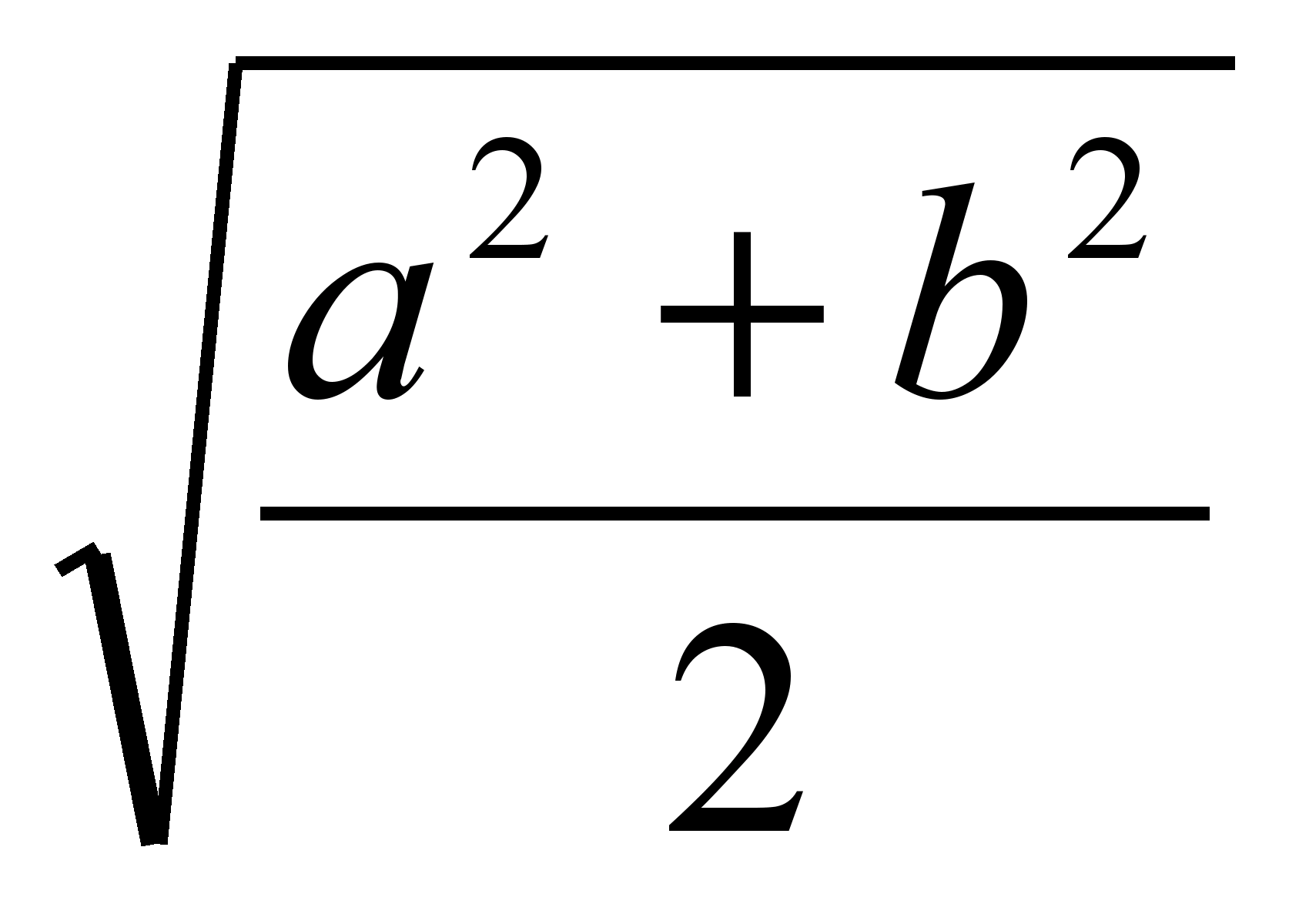 (среднему квадратичному длин оснований).
).
(среднему квадратичному длин оснований).
).
Теперь приводится тот же список уроков, что и краткие аннотации. В равнобедренной трапеции базовые углы конгруэнтны. Теорема 2. Если в трапеции базовые углы конгруэнтны, то трапеция является равнобедренной. Решенные проблемы В равнобедренной трапеции базовый угол составляет 73 °. Найдите все другие углы трапеции. В равнобедренной трапеции базовый угол в три раза меньше внутреннего угла в конце более короткого основания. Найдите все углы трапеции.
В трапеции, отрезок линии, оттянутый от середины боковой стороны, параллельной основаниям, пересекает другую боковую сторону в ее середине. Найдите длину трапеции в средней линии. В трапеции большая база имеет длину 27 см, а она на 10 см длиннее основания.
Чтобы учащиеся осознали связь между указанными отрезками, необходимо попросить построить их для данной трапеции. Без труда учащиеся построят среднюю линию трапеции и отрезок, проходящий через точку пересечения диагоналей трапеции параллельно основаниям. Где будет лежать третий и четвертый отрезок? Ответ на этот вопрос должен привести учащихся к открытию связи между средними величинами.
Найдите длины трапециевидных оснований. В равнобедренной трапеции две диагонали являются конгруэнтными. Задача 2. Если в трапеции две диагонали конгруэнтны, то трапеция равнобедренна. Задача 3. Любая точка на средней линии трапеции равноудалена от двух параллельных линий, содержащих основания трапеции. Если точка в плоскости эквидистантна от двух параллельных линий, содержащих основания трапеции, то точка принадлежит прямой, содержащей. трапеция в средней линии. Решенная проблема. В трапеции любой сегмент прямой линии, соединяющий точку на более коротком основании с точкой на большем основании, делят пополам на средней линии трапеции.
Признак и свойство вписанного и описанного четырехугольника должны быть конкретизированы для всех известных учащимся четырехугольников, в том числе и для трапеции.
Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.
Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.
В трапеции биссектрисы внутренних углов на концах боковой стороны пересекаются под прямым углом. В трапеции биссектрисы внутренних углов на концах боковой стороны пересекаются в точке, лежащей на средней линии трапеции. Задача 4. В равнобедренной трапеции базовый угол равен 60 °. Докажите, что более короткая базовая длина равна разности большей длины основания и длины боковой стороны.
В равнобедренной трапеции диагональ составляет 10 см и составляет 60 ° с основанием. Найдите длину трапеции средней длины. Основания трапеции имеют длину 3 и 5 единиц, одна диагональ перпендикулярна боковой стороне, а другая диагональ делит пополам угол. на большей базе. Найдите высоту трапеции. Используя линейку и компас, построим трапецию, у которой есть основания, совпадающие с двумя заданными сегментами, и боковые стороны, конгруэнтные. два других заданных сегмента.
Конкретизируем следствия для равнобедренной описанной трапеции :
|
|
высота равнобедренной описанной
равнобедренной трапеции есть среднее
геометрическое оснований трапеции.
Диагонали и углы трапецииИспользуя линейку и компас, построим трапецию, у которой есть основания, совпадающие с двумя заданными сегментами, а боковые стороны - конгруэнтные. к двум другим заданным сегментам. Геометрия - это особый предмет математики, который касается форм и объектов и связанных с ними проблем. Существуют разные типы геометрических фигур. Несколько важных двумерных фигур - это квадрат, прямоугольник, треугольник, многоугольник, круг, параллелограмм, трапеция, ромб и т.д. форма, ограниченная четырьмя сторонами, называется четырехсторонним. |
Рассмотрим основные принципы методики изучения свойств трапеции.
Во-первых, это использование задачного подхода . Нет необходимости вводить в теоретический курс геометрии новые свойства трапеции. Эти свойства открываются и формулируются учащимися через решение задач (лучше систем задач). Важно, чтобы учитель знал, какие задачи должны быть поставлены и в какой момент учебного процесса. Кроме того, каждое свойство может быть ключевой задачей в системе задач.
Во-вторых, «спиральная»
организация изучения свойств трапеции
.
К отдельным свойствам можно возвращаться
несколько раз, тогда есть вероятность,
что учащиеся их запомнят. Например,
свойство четырех точек можно доказать
при изучении подобия и потом с помощью
векторов. Равновеликость треугольников,
прилежащих к боковым сторонам трапеции,
можно доказать, используя как свойство
треугольников, имеющих равные высоты,
проведенные к сторонам, лежащим на одной
прямой, так и формулу
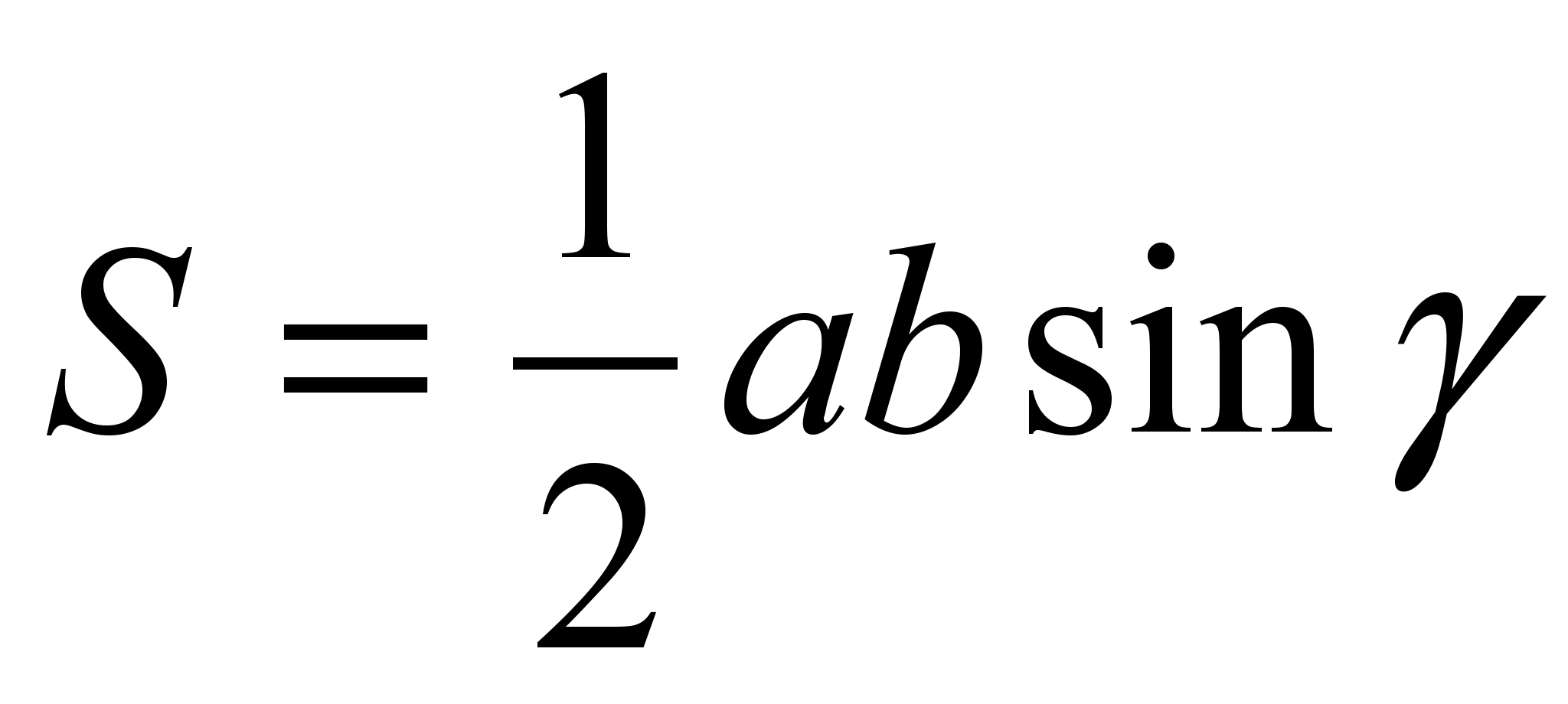 .
Можно отрабатывать свойства прямоугольного
треугольника на описанной трапеции,
теорему синусов на вписанной трапеции
и так далее.
.
Можно отрабатывать свойства прямоугольного
треугольника на описанной трапеции,
теорему синусов на вписанной трапеции
и так далее.
Предложенное включение «непрограммных» свойств трапеции в содержание школьного курса геометрии, задачная технология их изучения, неоднократное обращение к свойствам трапеции при изучении других тем позволят учащимся более глубоко познать трапецию и обеспечат успешность решения задач на применение ее свойств.
Поэтому одну из них мы назовем большим
, вторую - малым основанием
трапеции. Высотой
трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить "особый вид" высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР - накрестлежащие, ∠
ВМС=∠
DМР - вертикальные), поэтому ВМ=МР или точка М - середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР: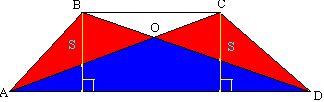 Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
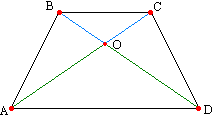
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так: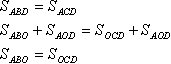
 Виды трапеций:
Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
 Свойства равнобокой трапеции:
Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
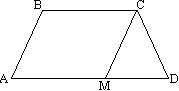
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD - равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.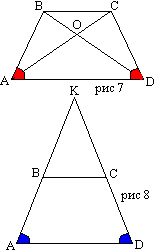 Теорема 11
. Диагонали равнобокой трапеции равны.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому АС=BD.
 Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.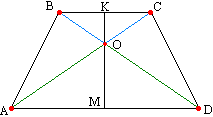 В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник)
Теорема 20
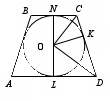
. Радиус вписанной в трапецию окружности равен половине высоты основания.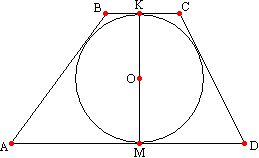 Доказательство этой теоремы заключается в объяснении того, что радиусы проведенные к основаниям лежат на высоте трапеции. Из точки О - центра вписанной в данную трапецию АВСD окружности проведем радиусы в точки касания её основаниями трапеции. Как известно, ридиус, проведенный в точку касания, перпендикулярен касатыльной, поэтому ОК^
ВС и ОМ^
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Доказательство этой теоремы заключается в объяснении того, что радиусы проведенные к основаниям лежат на высоте трапеции. Из точки О - центра вписанной в данную трапецию АВСD окружности проведем радиусы в точки касания её основаниями трапеции. Как известно, ридиус, проведенный в точку касания, перпендикулярен касатыльной, поэтому ОК^
ВС и ОМ^
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.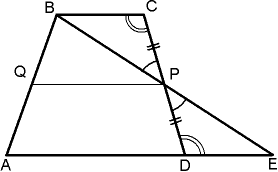
Доказательство:
Пусть ABCD - данная трапеция, а AB и CD - её основания. Пусть
также AH - высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
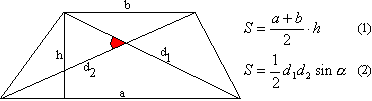 Вторая формула перешла от четырехугольника.
Вторая формула перешла от четырехугольника.
Возможно, будет полезно почитать:
- Талисманы китайской культуры, ошибочно приписываемые Фэн-шуй ;
- Сонник Лоффа — бывший муж ;
- Артикли в английском языке ;
- Большой энциклопедический словарь У вас более низкий риск развития диабета ;
- Молитва за человека который болеет раком ;
- План исследовательской работы и проекта ;
- Бухгалтер по расчету заработной платы (расширенный курс) Курсы по расчету заработной платы в 1с ;
- НТГ – нарушение толерантности к глюкозе: причины проявления, симптомы и методы коррекции ;
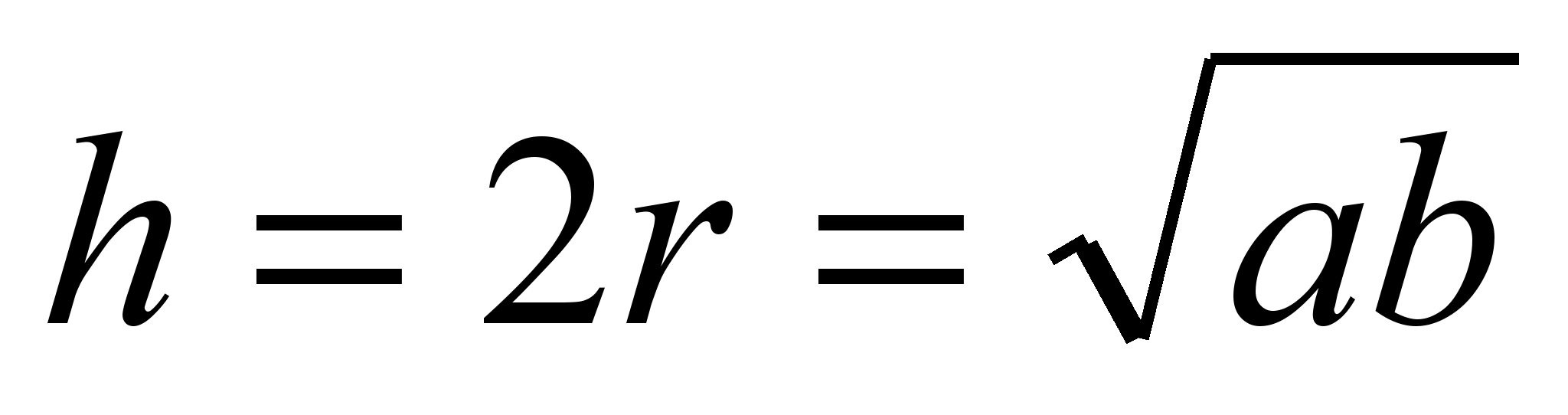 .
.