Ikkilamchi integralning asosiy xossalari. Ikki tomonlama integralning asosiy xossalarini qo'sh integral ta'rifi vazifasi Double integral asosiy tushunchalar va ta'riflar

Ikkilamchi integralning asosiy xossalari

Qo'sh integralning xossalari (va ularning hosilasi) yagona aniq integralning mos keladigan xususiyatlariga o'xshaydi.

1°. Qo'shimchalar. Agar funktsiya f(x, y) domenda integrallash mumkin D va agar hudud D egri chiziq yordamida G nol maydoni umumiy ichki nuqtalarsiz ikkita bog'langan mintaqaga bo'linadi D 1 va D 2 , keyin funksiya f(x, y) har bir domenda integrallash mumkin D 1 va D 2 , va

2°. Chiziqli xususiyat. Funktsiyalar bo'lsa f(x, y) Va g(x, y) domenda integrallash mumkin D, A α Va β har qanday haqiqiy sonlar bo'lsa, funktsiya [ α · f(x, y) + β · g(x, y)] domenida ham integrallash mumkin D, va

3°. Funktsiyalar bo'lsa f(x, y) Va g(x, y) domenda integrallash mumkin D, u holda bu funksiyalarning mahsuloti ham integrallanadi D.

4°. Funktsiyalar bo'lsa f(x, y) Va g(x, y) ikkalasi ham domenda integrallashtiriladi D va bu sohada hamma joyda f(x, y) ≤ g(x, y), Bu

5°. Agar funktsiya f(x, y) domenda integrallash mumkin D, keyin funksiya | f(x, y)| hududda integratsiyalashgan D, va

(Albatta, integrallikdan | f(x, y)| V D integratsiyalashuv kuzatilmaydi f(x, y) V D.)

6°. O'rtacha qiymat teoremasi. Agar ikkala funktsiya bo'lsa f(x, y) Va g(x, y) domenda integrallash mumkin D, funktsiyasi g(x, y) bu mintaqaning hamma joyida salbiy emas (ijobiy emas), M Va m- funksiyaning aniq yuqori va aniq pastki chegaralari f(x, y) hududda D, keyin raqam bor μ , tengsizlikni qondirish m ≤ μ ≤ M va formula shunday

Ikki tomonlama integral tushunchasiga olib keladigan masala Qo'sh integralning ta'rifi Qo'sh integralning asosiy xossalari Yassi mintaqaning maydoni Qo'sh integralni iteratsiyaga keltirish Ikki tomonlama integraldagi o'zgaruvchilarning o'zgarishi Egri chiziqli koordinatalardagi maydon elementi Yakobiy va uning geometrik ma'nosi qo'sh integraldagi o'zgaruvchilar formulasining o'zgarishi qutb koordinatalarida qo'sh integral

Ikki tomonlama integral tushunchasiga olib keladigan muammo. Ikki tomonlama integralning ta'rifi. Ikkilamchi integral tushunchasiga silindrsimon jismning hajmini hisoblashning aniq masalasini yechish orqali kelamiz. Silindrsimon jism - xOy tekisligi bilan chegaralangan jism, ba'zi sirt va silindrsimon sirt, generatorlari o'qga parallel (1-rasmga qarang). X va y o'zgaruvchilarning o'zgarishining D maydoni silindrsimon tananing asosi deb ataladi. Jismning hajmini aniqlashda ikkita tamoyildan kelib chiqamiz: !) agar tana qismlarga bo'lingan bo'lsa, u holda uning hajmi barcha qismlarning hajmlari yig'indisiga teng (qo'shilish xususiyati); 2) tekislik bilan chegaralangan z = const, xOy tekislikka parallel bo'lgan to'g'ri silindrning hajmi, poydevor maydonini balandlikka ko'paytirilganga teng. Keyinchalik, biz D domenini bog'langan (bir bo'lakdan iborat), kvadrat (ya'ni, maydonga ega) va chegaralangan (ya'ni, boshlang'ich markazida joylashgan qandaydir doira ichida joylashgan) deb faraz qilamiz. Z> sohasining hamma joyidagi P(x, y) nuqtaning uzluksiz funksiyasi bo‘lsin, ya’ni ko‘rib chiqilayotgan silindrsimon sirt butunlay xOy tekisligidan yuqorida yotadi. Silindrsimon jismning hajmini V bilan belgilaymiz. Silindrsimon jismning asosi D viloyatini ixtiyoriy shakldagi kesishmaydigan kvadratik mintaqalarning ma'lum soni n ga ajratamiz; biz ularni qisman mintaqalar deb ataymiz. Qisman hududlarni ma'lum bir tartibda raqamlagandan so'ng, hududlar - mos ravishda. Biz qisman mintaqaning diametrini Dk miqdor deb ataymiz, qo'sh integral tushunchasiga olib keladigan muammo Qo'sh integralning ta'rifi Qo'sh integralning asosiy xususiyatlari Yassi mintaqaning maydoni qo'sh integralni takrorlanganga qisqartirish O'zgaruvchilarning o'zgarishi qo'sh integralda Egri chiziqli koordinatalarda maydon elementi Yakobiy va uning geometrik ma'nosi Qo'sh integraldagi o'zgaruvchilar formulasi o'zgarishi Qutb koordinatalarida qo'sh integral bu erda p(P; Q) belgisi P va Q nuqtalari orasidagi masofani bildiradi. d ni belgilasin. qisman hududlar diametrlarining eng kattasi Dk (k = 1,2,...,n). Oz o'qiga parallel bo'lgan generatorlar bilan har bir qisman mintaqaning chegarasi orqali silindrsimon sirt chizamiz. Natijada silindrsimon korpus n ta qisman silindrsimon jismlarga bo'linadi. K-chi qisman jismni bir xil taglik va balandligi almashtirilgan yuzaning biron bir nuqtasi ilovasiga teng bo'lgan tekis silindr bilan almashtiramiz (2-rasm). Bunday silindrning hajmi nuqta Dk mintaqasining maydoni bo'lgan joydir. Har bir qisman silindrsimon jism uchun tasvirlangan konstruktsiyalarni bajarib, biz n-pog'onali jismni olamiz, uning hajmi (o) Vn kerakli hajmni V ni qanchalik aniq ifodalasa, Dk qismli mintaqalarning o'lchamlari shunchalik kichik bo'lishi intuitiv ravishda aniq. . Silindrsimon jismning V hajmini n pog'onali jismning hajmi (1) moyil bo'lgan chegaraga teng deb qabul qilamiz, chunki qisman mintaqalarning eng katta d diametri Dk nolga n intiladi. Tabiiyki, chegara D domenining qisman Dk domenlariga bo'linish turiga va qisman domenlarda Pk nuqtalarini tanlashga bog'liq bo'lmasligi kerak. /(x, y) D sohada aniqlangan ixtiyoriy funktsiya bo'lsin. n (1) yig'indisi f(x)y) funksiyaning ushbu sohaning berilgan bo'limiga mos keladigan D sohasi bo'yicha integral yig'indisi deyiladi. n qisman domenlar va Dk qisman domenlarda berilgan nuqtalar ®*,!/*) tanlovi. Ta'rif. Agar d - * 0 uchun D sohasini qisman sohalarga bo'lish usuliga yoki qisman sohalarda Pk nuqtalarni tanlashga bog'liq bo'lmagan n integral yig'indisining chegarasi mavjud bo'lsa, u holda u ning qo'sh integrali deyiladi. f(P) (yoki f(x, y )) funksiyasi D sohasi ustida va YOKI belgisi bilan belgilanadi Demak, (2) f(x, y) funksiyaning o‘zi D sohada integrallanuvchi deyiladi (f() P) - integrand, f(P) dS - integrand, dS - maydonning differentsial (yoki elementi), D mintaqasi - integrasiya mintaqasi; P (®, y) nuqta - o'zgaruvchan nozik integrasiya) . ,.. Silindrsimon jismga qaytsak, shunday xulosaga kelamiz: silindrsimon jismning xOy tekisligi, sirti va generatorlari Oz o'qiga parallel bo'lgan silindrsimon sirt bilan chegaralangan hajmi f(x) funksiyaning qo'sh integraliga teng. , y) silindrsimon jismning asosi bo'lgan D mintaqasi ustida. / YOKI Bu erda dx dy - Dekart koordinatalaridagi maydon elementi. Bu manfiy bo'lmagan funksiyaning qo'sh integralining geometrik ma'nosidir. Agar u holda hajm agar f (P) funksiyaning D hududida ham ijobiy, ham manfiy qiymatlarni qabul qilsa, u holda integral tananing xOy tekisligidan yuqorida joylashgan qismlarining hajmlarining algebraik yig'indisini ifodalaydi ( "+" belgisi) va tananing xOy tekisligi ostida joylashgan qismlari ("-" belgisi bilan olingan). Turli xil muammolar ikkita mustaqil o'zgaruvchining funktsiyasi uchun (1) shakldagi yig'indilarni tuzishga va keyinchalik chegaraga o'tishga olib keladi, bu nafaqat silindrsimon jismning hajmi masalasidir. Keling, integratsiyalashuv uchun etarli shartlarni tuzamiz. Teorema 1. Chegaralangan yopiq sohada uzluksiz y) har qanday funktsiya bu sohada integrallanadi. Integrandning uzluksizligiga bo'lgan talab ko'pincha juda cheklangan. Ilovalar uchun quyidagi teorema muhim bo'lib, u ma'lum bir uzluksiz funksiyalar sinfi uchun qo'sh integral mavjudligini kafolatlaydi. Biz aytamizki, tekislikdagi ba'zi nuqtalar to'plami, agar u ixtiyoriy ravishda kichik maydonning ko'pburchak shakliga o'ralishi mumkin bo'lsa, uning maydoni nolga teng. Teorema 2. Agar f(x, y) funksiya yopiq chegaralangan D sohasi bilan chegaralangan bo‘lsa va nol sohaning ayrim nuqtalari to‘plamidan tashqari D ning hamma joyida uzluksiz bo‘lsa, u holda bu funksiya D sohada integral bo‘ladi. §2. Ikkilamchi integralning asosiy xossalari Ikki tomonlama integrallar bitta mustaqil o'zgaruvchining funksiyalari uchun aniq integralning xossalariga o'xshash bir qator xususiyatlarga ega. 2.1. Chiziqli xossa Agar a) funksiyalar D sohada integrallansa, a va p ixtiyoriy haqiqiy sonlar bo lsa, u holda af) funksiya ham D sohasida integrallanadi va o) 2.2. Tengsizliklar integrasiyasi Agar funksiyalar) D sohada va shu sohaning hamma joyida integrallansa, u holda (2), ya’ni tengsizliklar integrallanishi mumkin. Xususan, aniq tengsizliklarni integrallashgan holda, biz tekis hududning maydonini olamiz D tekis mintaqaning maydoni bir ga teng bo'lgan funktsiyaning ushbu mintaqasi ustidagi qo'sh integralga teng. Darhaqiqat, D sohasida /(P) = 1 funktsiyasi uchun integral yig'indisi shaklga ega va D sohasining qisman Dt sohalariga bo'linishi uchun, uning maydoniga teng S. Ammo keyin bu yig'indining chegarasi, ya'ni. , qo'sh integral, S maydoniga teng D sohalari: yoki, bir xil, (3) 2.4. Integralni taxmin qilish /(P) funksiya chegaralangan yopiq D hududida uzluksiz bo'lsin, M va mn D mintaqasidagi /(P) ning eng katta va eng kichik qiymatlari, 5 esa uning maydoni bo'lsin. Keyin (4) 2.5. Qo'shimchalilik: Agar /(P) funksiya D sohada integrallansa va Z) domen umumiy ichki nuqtalarsiz ikkita D\ va Di sohalariga bo'lingan bo'lsa, u holda /(P) D\ va Di domenlarining har birida integrallanadi. , va (5) 2.6. O'rtacha qiymat haqidagi teorema 3-teorema (o'rtacha qiymat bo'yicha). Agar /(P) funktsiyasi yopiq chegaralangan D hududida uzluksiz bo'lsa, u holda u formulasi o'rinli bo'lishi uchun D mintaqasining kamida bitta Pc nuqtasi mavjud bo'ladi, bu erda S - D hududining maydoni D, u holda u D dagi eng katta M qiymatini va eng kichik qiymatini m ni oladi.4-xususiyatga ko‘ra, integralning bahosi bo‘yicha, P) D sohasi bo‘yicha, u qaysidir nuqtada Pc G D shu songa teng qiymatni oladi, bundan S The (7) formula bilan aniqlangan f(Pc) qiymati f(P) funksiyaning o’rtacha qiymati deyiladi D. qiymat Agar D hududida /(P) ^ O funksiya bo’lsa, (6) formula shuni bildiradi. asosi D (uning maydoni 5) va balandligi H = / (Pc) bo'lgan tekis silindr mavjud bo'lib, uning hajmi silindrsimon tananing hajmiga teng (rasm). 3). § 3. Ikkilamchi integralni takrorlanuvchi integralga keltirish Ikki tomonlama integralni hisoblashning samarali usullaridan biri uni takrorlangan integralga keltirishdir. 3.1. To'g'ri to'rtburchakning holati D mintaqasi tomonlari koordinata o'qlariga parallel bo'lgan yopiq to'rtburchak P bo'lsin. P to'rtburchakda f(x, y) funksiya uzluksiz bo'lsin. Ikkilamchi integralni asosi P sirt bilan chegaralangan silindrsimon jismning (algebraik) hajmi deb talqin qilish mumkin.. Tegishli silindrsimon jismni ko'rib chiqaylik. Oy o'qiga perpendikulyar tekislik chizamiz (4-rasm). Bu tekislik silindrsimon jismni egri chiziqli trapetsiya bo'ylab kesib tashlaydi, yuqoridan tekis chiziq z bilan chegaralangan, tenglamalar bilan tavsiflanadi ABB\A\ trapesiyaning maydoni x ustida integratsiya amalga oshiriladigan integral bilan ifodalanadi va yo - integrandning ikkinchi argumenti - doimiy sifatida qabul qilinadi ). (1) integralning qiymati y0 qiymatini tanlashga bog'liq. Biz (2) ifodasini o'rnatamiz (2) silindrsimon jismlarning ko'ndalang kesimi maydonini y funktsiyasi sifatida beradi. Shuning uchun silindrsimon jismning hajmini formula bilan hisoblash mumkin. Boshqa tomondan, bu hajm P to'rtburchaklar ustidagi /(x, y) funksiyaning qo'sh integrali bilan ifodalanadi. Demak, S(y) ni uning bilan almashtiramiz. (2) ifodada biz qo'sh integral tushunchasiga olib keladigan muammoni olamiz. integral Egri chiziqli koordinatadagi maydon elementi Yakobiy va uning geometrik ma'nosi Ikki tomonlama integraldagi o'zgaruvchilar formulasi Qutbli koordinatalarda qo'sh integral Oxirgi munosabat odatda quyidagicha yoziladi Silindrsimon jismning hajmini silindrsimon jismning ko'ndalang kesimi maydonlari orqali ham topish mumkin. tekisliklar x = x0. Bu (4) formulaga olib keladi (3) va (4) formulalarning o'ng tomonidagi ifodalarning har biri f(x, y) funktsiyasini oddiy integrallashning ketma-ket ikkita amalini o'z ichiga oladi. Ular f(x, y) funksiyaning n sohasi bo‘yicha takrorlangan integrallari deyiladi.Agar f(x, y) yopiq to‘rtburchakda n uzluksiz bo‘lsa, u holda takrorlangan integrallarga o‘tish har doim ham mumkin bo‘ladi va (5) ya’ni. uzluksiz funksiya /(x, y) ning takrorlangan integrallarining qiymatlari integrallash tartibiga bog'liq emas. Misol 1. Bizda mavjud bo'lgan maydon ustidagi funktsiyaning qo'sh integralini toping (5-rasmga qarang): 3.2. Ixtiyoriy sohaning ishi Endi integrasiya sohasi xOy tekisligidagi ixtiyoriy chegaralangan kvadratik yopiq D sohasi bo‘lib, quyidagi shartni qanoatlantiramiz: Oy o‘qiga parallel bo‘lgan har qanday to‘g‘ri chiziq D sohasi chegarasini dan ko‘p bo‘lmagan nuqtada kesib o‘tadi. ikki nuqta yoki butun segment bo'ylab (rasm. . 6 a). To'rtburchak ichida D maydonini rasmda ko'rsatilganidek o'rab olamiz. 66. [a, 6] segmenti D mintaqasining Oksi o'qiga ortogonal proyeksiyasi, [c, dj segmenti D mintaqasining Oy o'qiga ortogonal proyeksiyasidir. A va C nuqtalari bo'yicha D hududining chegarasi ABC va AEC ikkita egri chizig'iga bo'linadi. Bu egri chiziqlarning har biri Oy o'qiga parallel bo'lgan ixtiyoriy to'g'ri chiziq bilan bir nuqtadan ko'p bo'lmagan holda kesishadi. Shuning uchun ularning tenglamalarini y uchun ruxsat etilgan shaklda yozish mumkin: f(x, y) D sohada uzluksiz ba'zi funksiya bo'lsin. Ko'rib chiqilayotgan silindrsimon jismni tekislik bilan kesamiz. Bo'limda biz PQMN egri chiziqli trapesiyani olamiz (7-rasm), uning maydoni bitta y o'zgaruvchining funktsiyasi sifatida qabul qilingan / (x, y) funktsiyasining oddiy integrali bilan ifodalanadi. Bunda y o'zgaruvchisi P nuqta ordinatasidan Q\ nuqta ordinatasiga o'zgaradi P nuqta x = const (tekislikdagi) chiziqning mintaqaga *!-ka "kirishi" - uning ushbu mintaqadan "chiqish" nuqtasi. ABC egri chizig'i va egri chiziq uchun tenglama mavjud bo'lganligi sababli, x olinganda bu ordinatalar mos ravishda teng bo'ladi. Shuning uchun, integral bizga silindrsimon jismning tekis kesimining maydoni uchun sekant tekisligining x = const pozitsiyasiga bog'liq bo'lgan ifodani beradi. Butun jismning hajmi o'zgarish oralig'ida w bu ifodaning integraliga teng bo'ladi. Shunday qilib, Xususan, D mintaqasining S maydoni uchun biz olamiz Keling, har bir chiziq D mintaqasining chegarasini mos ravishda abscissalari teng bo'lgan ikkita P va Q nuqtada kesishadi deb faraz qilaylik (yoki bo'ylab). butun segment) (8-rasm). Shunga o'xshash mulohazalarni amalga oshirib, biz qo'sh integralning hisobini takroriy integralga kamaytiradigan formulaga erishamiz. 2-misol. Chiziqlar bilan chegaralangan D maydoni ustida funksiyaning qo'sh integralini hisoblang ^ Birinchi yo'l. Integrallash viloyatini D tasvirlaymiz. y = x chiziq va y = x2 parabola nuqtalarda kesishadi). Bu shuni anglatadiki, x 0 dan 8 chegarada o'zgaradi. Har qanday to'g'ri chiziq x = const) mintaqaning chegarasini ko'pi bilan ikki nuqtada kesib o'tadi. Shuning uchun (8) formula qo'llaniladi: Ikkinchi usul (10-rasm). Formulani qo'llash (10). xuddi shunday natijaga erishamiz: 3-misol. Sirt bilan chegaralangan jismning xOy tekisligi bilan ellips chizig‘i bo‘ylab yarim o‘qlar bilan kesishgan jismning xOx va y koordinata tekisliklariga nisbatan simmetriyasi tufayli hajmini hisoblab chiqamiz: Izoh. Agar D sohasi shunday bo'lsaki, ba'zi to'g'ri chiziqlar (ortogonal yoki gorizontal) uning chegarasini ikkidan ortiq nuqtada kesib o'tsa, u holda D sohasi ustidagi qo'sh integralni hisoblash uchun uni mos keladigan tarzda qismlarga bo'lish kerak. integrallarni qismlarga integratsiyalashni takrorlang va natijalarni qo'shing. 4-misol. Agar ichki kvadratning tomoni 2, tashqisi 4 bo'lsa, markazlari bo'lgan ikkita kvadrat orasiga va koordinata o'qlariga parallel bo'lgan koordinata boshi va tomonlari bilan o'ralgan D maydoni bo'yicha qo'sh integralni hisoblang. tomoni 4 ga teng bo'lgan katta Q kvadratda va tomoni 2 ga teng bo'lgan kichik kvadrat R.da (12-rasm). 1-teoremaga ko'ra, e*** funktsiyasining ko'rsatilgan kvadratlar ustidagi integrallari mavjud bo'lib, kerakli integralning qiymati §4. Ikkilamchi integraldagi o'zgaruvchilarning o'zgarishi 4.1. Nuqtaning egri chiziqli koordinatalari tushunchasi uOv tekislikning D* sohasida funksiyalar juftligi berilsin, biz ularni shu sohada uzluksiz va uzluksiz qisman hosilalarga ega deb hisoblaymiz. (1) tenglama tufayli D* mintaqaning har bir M*(x, v) nuqtasi xOy tekisligidagi bitta aniq M(x, y) nuqtaga to‘g‘ri keladi va shu tariqa D* mintaqa nuqtalariga mos keladi. xy tekislikdagi (x, y) nuqtalarning ma'lum D to'plami (13-rasm). Bunda (1) funksiyalar D4 mintaqani D to‘plamga joylashtirish uchun aytiladi. Faraz qilaylik, turli nuqtalar (u, v) turli nuqtalarga (x, y) mos kelsin. Bu (1) tenglamalarning u, v ga nisbatan yagona yechish qobiliyatiga ekvivalentdir: Bu holda, xaritalash D* domenini D domeniga birma-bir xaritalash deb ataladi. Bunday transformatsiya ostida har qanday D* sohasida yotgan uzluksiz egri L* uzluksiz egri chiziq D mintaqasida yotuvchi L uzluksiz egri chizig'iga o'tadi. Agar q(x) y) va h(x, y) funktsiyalari ham uzluksiz bo'lsa, transformatsiya yordamida har qanday uzluksiz chiziqli LCD. (2) L* C D* uzluksiz chiziqdan o'tadi. D* mintaqasidan u, v o'zgaruvchilar qiymatlarining berilgan W, Vo juftligi uchun nafaqat M*(u) nuqtasining o'rnini yagona aniqlash mumkin.<)> Vq) sohaning o'zi p)*, lekin D sohasida mos keladigan M(xo, yo) nuqtaning o'rni, xo = 4>(o, v0), 3/0 = o, vo). Bu u, v sonlarini xOy tekisligidagi M mintaqaning D nuqtasining ba'zi yangi koordinatalari sifatida ko'rib chiqishga asos beradi. Ular M nuqtaning egri chiziqli koordinatalari deyiladi. Koordinatalaridan biri doimiy bo'lib qoladigan D mintaqasidagi nuqtalar to'plami koordinata chizig'i deyiladi. (1) formulada u = vq deb faraz qilsak, koordinata chizig'ining parametrik tenglamalarini olamiz, Bu erda parametr rolini u o'zgaruvchisi bajaradi. Koordinata v ga har xil (u uchun mumkin) doimiy qiymatlarni berib, xOy tekisligida koordinata chiziqlari turkumini (v = const) olamiz. Xuddi shunday, biz koordinata chiziqlarining yana bir oilasini olamiz (u = const). Agar D* va D mintaqalari oʻrtasida yakkama-yakka moslik mavjud boʻlsa, bir oilaning turli koordinata chiziqlari bir-biri bilan kesishmaydi va har bir turkumdan bittadan chiziq D mintaqasining istalgan nuqtasidan oʻtadi. XOp tekisligidagi egri chiziqli koordinatali chiziqlar to'ri uOv tekisligidagi to'rtburchaklar panjaraning tasviridir (13-rasmga qarang). 4.2. Egri chiziqli koordinatalarda maydon elementi. Yakobiy va uning geometrik ma'nosi D* mintaqasida Uo*V tekisligida tomonlari 0*u va O"v koordinata o'qlariga parallel bo'lgan kichik P*P?P$Pl to'rtburchakni va ularning uzunliklarini ajratib olaylik. tomonlari Au va Av (aniqlik uchun A ) deb faraz qilamiz (14-rasm a) Uning maydoni To'rtburchak D hududida egri chiziqli to'rtburchak * ga aylanadi (146-rasm).Agar cho'qqilar P) koordinatalariga ega bo'lsa, u holda , formulalarga (1) ko'ra, Pi ning mos cho'qqilari koordinatalariga ega), Ikki o'zgaruvchining funktsiyasi uchun Teylor formulasidan foydalanib va Au va Av ga nisbatan birinchi tartib / kompyuter shartlari bilan cheklanib, biz quyidagi taxminiy qiymatni olamiz. to'rtburchak cho'qqilari uchun koordinatalarning qiymatlari, bu erda funktsiyalar, ularning barcha hosilalari bir nuqtada hisoblanadi.. tartibli to'rtburchak P\PiPiPa parallelogramma Bu shundan kelib chiqadiki, U holda to'rtburchakning DS maydoni taxminan ifodalanishi mumkin. vektor mahsulotining uzunligi bo'yicha, qo'sh integral tushunchasiga olib keladigan muammo Qo'sh integralning ta'rifi Ikki tomonlama integralning asosiy xossalari Yassi mintaqaning maydoni qo'sh integralning iteratsiyaga qisqarishi O'zgaruvchilarning o'zgarishi qo'sh integral Egri chiziqli koordinatadagi maydon elementi Yakobiy va uning geometrik ma'nosi Ikkilamchi integraldagi o'zgaruvchilar formulasi Qutb koordinatalarida qo'sh integral O'zgartirish formulalari (1) yordamida D sohasiga ko'rsatilganda aniqlovchi nuqta (tx, v)). 4.3. Ikkilamchi integraldagi o'zgaruvchilar formulasi Uzluksiz funktsiyalar D* sohasini D ga birma-bir xaritalashni amalga oshirsin va birinchi tartibli uzluksiz qisman hosilalarga ega bo'lsin. xOy tekisligida D sohada uzluksiz funksiya berilsin.Funksiyaning har bir qiymati) D sohasidagi r = funksiyaning D sohasidagi teng qiymatiga mos keladi, bunda (u, v) va (x) , y) ulardagi funksiyalarning qiymatlari mos kelishi uchun va D va D* sohalari bo‘yicha z = /(x, y) va v) funktsiyalari uchun integral yig‘indilarni tuzamiz. (9) chegaraga qadar, chunki qisman hududlarning eng katta diametri d* D\ nolga intiladi (xaritalashning uzluksizligi (I) tufayli D dagi qisman hududlarning d diametrlarining eng kattasi ham moyil bo'ladi). nolga), bizda J F 0 shart shart Teorema 4. Dekart koordinatalarida berilgan qo'sh integralni egri chiziqli koordinatalarda qo'sh integralga aylantirish uchun integralda x va y o'zgaruvchilarni almashtirish kerak. f(x, y), mos ravishda orqali va maydon elementi dx dy - uning egri chiziqli koordinatalarda ifodalanishi: Misol. Giperbola m bilan chegaralangan figuraning maydonini toping. Ko'rsatilgan raqamning maydonini topish O mintaqasi bo'yicha qo'sh integralni hisoblashga qisqartiriladi. Keling, formulalar bo'yicha yangi, egri chiziqli u va o koordinatalarini kiritaylik. Demak, uOv tekislikda biz to'rtburchak (156-rasm) - berilgan D figuradan oddiyroq shaklga ega bo'ldik. (11) u va t> ga bog'langan munosabatlardan x va y ni ifodalaymiz: 15-rasm Keyin qutbdagi Double integral. Koordinatalar Ikki tomonlama integralni hisoblash ko'pincha to'rtburchaklar koordinatalarini x va y formulalar bo'yicha qutb koordinatalari bilan almashtirish orqali soddalashtiriladi Qutb koordinatalarida maydon elementi Dekart koordinatalarida integraldan qutb koordinatalarida integralga o'tish shakli va formulasiga ega. quyidagicha yozilishi mumkin: Bu holda (13) qutb koordinatalaridagi maydon elementi va geometrik mulohazalardan olinishi mumkin (16-rasmga qarang). A \u003d pl rasmida soyalangan maydonning maydoni. tarmoqlar. sektorlar Yuqori tartibli cheksiz kichik qiymatdan voz kechsak, biz qutb koordinatalarida maydon elementini olamiz va qabul qilamiz. Demak, Dekart koordinatalarida qo‘sh integralni qutb koordinatalarida qo‘sh integralga aylantirish uchun integralda a: va y ni mos ravishda p costp va psiy bilan almashtirish va dekart koordinatalaridagi maydon elementini dx dy maydon bilan almashtirish kerak. qutb koordinatalaridagi element p dp dip. Keling, qutb koordinatalarida qo'sh integralni hisoblash bilan shug'ullanamiz. To'g'ri to'rtburchak Dekart koordinatalarida bo'lgani kabi, qutb koordinatalarida integralni hisoblash uni takrorlangan integralga keltirish yo'li bilan amalga oshiriladi. Avval O qutb berilgan D mintaqasidan tashqarida joylashgan holatni ko‘rib chiqamiz. D mintaqasi qutbdan chiqadigan har qanday nurga xos xususiyatga ega bo‘lsin (koordinata chizig‘i y uning chegarasini ko‘pi bilan ikki nuqtada yoki butun segment bo‘ylab kesib o‘tadi () 17-rasm).Polar burchakning ekstremal i qiymatlari tashqi integrasiya chegaralari ekanligiga e'tibor bering.Q> = nuri D mintaqasi konturining A nuqtasidan, nur esa B nuqtasidan o'tadi. nuqtalar Aw B D mintaqasi konturini ikki qismga ajratadi: ACB va AFB.Ularning qutb tenglamalari bo’lsin, bu yerda) shartni qanoatlantiruvchi bir qiymatli uzluksiz funksiyalar funksiyalar ichki integrasiya chegaralari. Takrorlangan integrallarga o'tib, quyidagi formulani olamiz Xususan, F(p, r 1) uchun D sohasining S maydoni uchun faqat bir nuqtada yoki butun segment bo'ylab mintaqa chegarasini olamiz (18-rasm) - qutb koordinatalarida mintaqa chegarasi tenglamasi Keyin 18-rasm. Masalan, mintaqa birinchi kvadrantda joylashgan birlik doiraning chorak qismi bo'lgan integralni hisoblang Qutb koordinatalariga o'tamiz Keyin integrasiya maydoni a. to'rtburchak O'zgartirilgan integral / hisoblash oson: r Izoh: Agar D domenida yakobiy nolga teng bo'lmasa, u holda ushbu sohaning har bir nuqtasining ba'zi bir qo'shnilarida xaritalash birma-bir bo'lishi mumkin, lekin shunday bo'lishi mumkin: butun domenni xaritalash birma-bir emas.Funktsiyalar bilan aniqlangan xaritalashni ko'rib chiqaylik.Bu funksiyalarning yakobiyi hamma joyda nolga teng va shuning uchun ham nolga teng emas. Shunga qaramay, biz olish uchun, shuning uchun bu xaritalash bir-bir emas. Boshqa tomondan, agar xaritalashning yakobiyi bir nuqtada yo'qolib qolsa, shunga qaramay, bu nuqtaning qo'shnisida xaritalash birma-bir bo'lib chiqishi mumkin. Masalan, funksiyalar bilan aniqlangan xaritalash uchun Yakobiy nolga va at ga teng, lekin xaritalash birma-bir. Teskari xaritalash funksiyalar bilan belgilanadi

1.1 Qo'sh integralning ta'rifi

1.2 Ikki tomonlama integralning xossalari

Qo'sh integralning xossalari (va ularning hosilasi) yagona aniq integralning mos keladigan xususiyatlariga o'xshaydi.

1°. Qo'shimchalar. Agar f(x, y) funksiya D sohada integrallansa va D sohasi nol maydonning G egri chizig‘i bilan umumiy ichki nuqtalarsiz ikkita bog‘langan D 1 va D 2 sohalariga bo‘lingan bo‘lsa, u holda f(x, y) har birida D 1 va D 2 mintaqalaridan integrallanadi va

2°. Chiziqli xususiyat. Agar f(x, y) va g(x, y) funktsiyalari D sohasida integrallash mumkin bo'lsa, shundaymi? Va? - har qanday haqiqiy sonlar, keyin funksiya [? f(x, y) + ? g(x, y)] ham D sohasida integrallanadi va

3°. Agar f(x, y) va g(x, y) funksiyalar D sohada integrallansa, bu funksiyalarning ko‘paytmasi D sohasida ham integrallanadi.

4°. Agar f(x, y) va g(x, y) funktsiyalari ikkalasi D sohada va shu f(x, y) sohaning hamma joyida integrallansa? g(x, y), keyin

5°. Agar f(x, y) funksiya D sohada integrallansa, u holda |f(x, y)| D domenida integrallash mumkin, va

(Albatta, D dagi |f(x, y)| ning integrallanishi D dagi f(x, y) ning integrallanishini anglatmaydi).

6°. O'rtacha qiymat teoremasi. Agar ikkala f(x, y) va g(x, y) funksiyalar D sohada integrallansa, g(x, y) funksiya bu sohaning hamma joyida manfiy emas (musbat emas), M va m funksiyalar f( x, y) funksiyaning D sohasidagi eng yaxshi yuqori va quyi chegaralari, u holda m tengsizlikni qanoatlantiruvchi son mavjud? ? ? M va shunday formula bo'ladi

Xususan, agar D da f(x, y) funksiya uzluksiz bo‘lib, D sohasi bog‘langan bo‘lsa, bu sohada shunday nuqta (?, ?) mavjud bo‘lsa, nima? = f(?, ?) va formulaga aylanadi

7°. Muhim geometrik xususiyat. D hududining maydoniga teng

T tanasi fazoda berilgan bo'lsin (2.1-rasm), pastdan D mintaqasi bilan, yuqoridan - uzluksiz va manfiy bo'lmagan funksiya grafigi bilan chegaralangan) z \u003d f (x, y,) aniqlangan. mintaqada D, yon tomondan - silindrsimon sirt bilan, uning yo'riqchisi D chegara sohasi va generatorlar Oz o'qiga parallel. Bunday turdagi jismga silindrsimon tana deyiladi.

1.3 Ikki tomonlama integralning geometrik talqini

1.4 To'rtburchak uchun qo'sh integral tushunchasi

R = to'rtburchakning hamma joyida ixtiyoriy f(x, y) funksiya aniqlansin? (1-rasmga qarang).

a segmentini ajratamiz? x? b a = x 0 nuqtalari yordamida n ta qisman segmentlarga< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Ox va Oy o'qlariga parallel to'g'ri chiziqlar yordamida bu bo'linish R to'rtburchakning n · p qisman to'rtburchaklarga bo'linishiga mos keladi R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). R to'rtburchakning ko'rsatilgan qismi T belgisi bilan belgilanadi. Keyingi bo'limda "to'rtburchak" atamasi tomonlari koordinata o'qlariga parallel bo'lgan to'rtburchakni anglatadi.

Har bir qisman R kl to'rtburchakda ixtiyoriy nuqtani (? k , ? l) tanlaymiz. ?x k = x k - x k-1 , ?y l = y l - y l-1 ni qo'yib, R kl to'rtburchakning maydonini R kl bilan belgilaymiz. Shubhasiz, ?R kl = ?x k ?y l.

R to'rtburchakning berilgan T bo'limiga va T bo'limning qisman to'rtburchaklaridagi oraliq nuqtalarning (?k, ?l) berilgan tanloviga mos keladigan f(x, y) funksiyaning integral yig'indisi deyiladi.

Diagonal to'rtburchakning diametri deb ataladi R kl . Belgimi? barcha qisman to'rtburchaklar diametrlarining eng kattasini belgilang R kl .

I soni integral yig'indilar chegarasi (1) deb ataladi? Har qanday ijobiy raqam uchun > 0? shunday ijobiy raqamni ko'rsata olasizmi?, agar?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - Men |< ?.

Agar R to'rtburchakda f(x, y) funksiya integral yig'indilarining chekli I chegarasi mavjud bo'lsa, R to'rtburchakda integrallanadigan (Rimanga ko'ra) funksiya deyiladi? > 0.

Bu I chegara f(x, y) funksiyaning R to‘rtburchak ustidagi qo‘sh integrali deyiladi va quyidagi belgilardan biri bilan belgilanadi:

Izoh. Xuddi bir martalik aniq integralga o'xshab, R to'rtburchakda integrallanadigan har qanday f(x, y) funksiya shu to'rtburchakda chegaralanganligi aniqlanadi.

Bu faqat f(x, y) cheklangan funksiyalarni ko'rib chiqishga asos beradi.

Ikki tomonlama integral tushunchasiga olib keladigan muammo.

Faraz qilaylik, bo'laklarning funksiyasi aniqlangan va summani yozing

bu integral deb ataladi.

Javob: Funksiya va tanlovning aniq integrali (d.i.) ostida

Belgilash:

Raqamlar integrallanuvchi deb ataladi (Rimanga ko'ra).

T. mavjudligi: Shu shart bilan.

O.i.ning taʼrifiga muvofiq. e'tibor bering, integral shaklga, chegaralarga va ga bog'liq, lekin o'zgarmaydigan belgilash belgisiga bog'liq emas, aks holda ifodalangan

17.1.1 va 17.1.2-bandlarga muvofiq va o.i. egri chiziqli trapezoidning maydoni uchun formulalarni yozamiz: , ish kuchi

kuni:

Qo'sh integral, integral yig'indi haqida tushuncha.

Ikki tomonlama integralning mavjudligi, ya'ni uchun integral yig'indisining chegarasi aniq ko'rinadi, chunki bu chegara silindrsimon jismning hajmini beradi. Biroq, bu fikr qat'iy emas. To'liqroq kurslarda bu tasdiq qat'iy isbotlangan va qo'sh integral mavjudligi teoremasi deb ataladi.

Borliq teoremasi. Maydoni a bo'lgan chegaralangan yopiq mintaqada uzluksiz bo'lgan har qanday funktsiya uchun qo'sh integral mavjud, ya'ni kichik maydonlar sonining cheksiz ko'payishi bilan integral yig'indilarning chegarasi mavjud bo'lib, ularning har biri bir nuqtaga qisqarishi sharti bilan. . Bu chegara mintaqani qismlarga bo'lish usuliga ham, nuqtalarni tanlashga ham bog'liq emas

Keyinchalik, biz faqat integratsiya sohasida uzluksiz bo'lgan funktsiyalarni ko'rib chiqamiz.

Mavjudlik teoremasidan kelib chiqadiki, masalan, a mintaqani koordinata o'qlariga parallel bo'lgan to'g'ri tomonlari kichik to'rtburchaklarga bo'lishimiz mumkin (230-rasm). Qayerda. Keyin har bir kichik to'rtburchakda nuqta tanlab, biz qo'sh integralning ta'rifiga ko'ra yozishimiz mumkin.

Qo'sh integralni shakl yig'indisining chegarasi sifatida olish mumkinligini ta'kidlash uchun belgi o'rniga yozuv ham qo'llaniladi.

Bu ifoda Dekart koordinatalarida maydon elementi deb ataladi va tomonlari koordinata o'qlariga parallel bo'lgan to'rtburchaklar maydoniga teng.

E'tibor bering, integral yig'indini tuzishda a hududining chegarasiga tutashgan maydonlar to'rtburchaklar shakliga ega emas. Biroq, bunday maydonlarni to'rtburchaklar bilan chegaradagi maydonlar bilan almashtirish xatosi nolga kamayishi isbotlanishi mumkin.

Ikki tomonlama integrallarning xossalari

Qo'sh integralning xossalari (va ularning hosilasi) yagona aniq integralning mos keladigan xususiyatlariga o'xshaydi.

3°. Funktsiyalar bo'lsa f(x, y) Va g(x, y) domenda integrallash mumkin D, u holda bu funksiyalarning mahsuloti ham integrallanadi D.

4°. Funktsiyalar bo'lsa f(x, y) Va g(x, y) ikkalasi ham domenda integrallashtiriladi D va bu sohada hamma joyda f(x, y) ≤ g(x, y), Bu

5°. Agar funktsiya f(x, y) domenda integrallash mumkin D, keyin funksiya | f(x, y)| hududda integratsiyalashgan D, va

(Albatta, integrallikdan | f(x, y)| V D integratsiyalashuv kuzatilmaydi f(x, y) V D.)

Xususan, agar funktsiya f(x, y) ichida davom etadi D, va hudud D ulangan, keyin bu sohada shunday nuqta bor ( ξ , η ), Nima μ = f(ξ , η ) va formula (11) shaklni oladi

Ikki o'zgaruvchining funktsiyasi uchun, deb belgilangan z = f(x, y) .

Ikki tomonlama integral quyidagicha yoziladi:

Bu yerga D- chiziqlar bilan chegaralangan tekis figura, uning ifodalari (tengliklari) qo'sh integralni hisoblash topshirig'ida berilgan. Chap va o'ng - tenglik, bunda o'zgaruvchi chap tomonda x, va yuqorida va pastda - tenglik bo'yicha, bunda o'zgaruvchi chap tomonda y. Bu va undan keyingi joy qo'sh integralni hisoblash texnikasini tushunish uchun eng muhimlaridan biridir.

Ikki tomonlama integralni hisoblash - ko'rsatilgan raqamning maydoniga teng raqamni topishni anglatadi D .

Biz tegguncha qo'sh integralning ta'riflari , va biz uni hisoblashni o'rganamiz. Ikki tomonlama integral nima ekanligini, uni hisoblash uchun bir nechta masalalar yechilganida tushunish osonroq bo'ladi, shuning uchun siz ushbu dars oxirida qo'sh integralning ta'rifini topasiz. Biroz oldinga qarab, shuni ta'kidlashimiz mumkinki, qo'sh integralning ta'rifi ham aytib o'tilgan raqam bilan bog'liq. D .

Agar raqam D to'rtburchak bo'lib, uni chegaralovchi barcha chiziqlar to'g'ri chiziqlardir. Agar raqam D- egri chiziqli, keyin chap va o'ngda to'g'ri chiziqlar bilan, yuqoridan va pastdan esa - topshiriqda berilgan tenglik bilan berilgan egri chiziqlar bilan chegaralanadi. Raqam bo'lgan holatlar ham mavjud D- uchburchak, lekin bunday holatlar haqida bir oz ko'proq.

Ikkilamchi integralni hisoblash uchun, shuning uchun raqamni chegaralovchi chiziqlarni tartiblash kerak D, bu qat'iy nomga ega - integratsiya mintaqasi. Chapga va o'ngga, yuqoriga va pastga qarab tartiblang. Bu qachon talab qilinadi qo'sh integralni takrorlangan integralga qisqartirish – qo‘sh integralni hisoblash usuli.

To'rtburchaklar maydoni:

Egri chiziqli mintaqa holati:

Va bu allaqachon bizga tanish bo'lgan aniq integrallarning yechimi bo'lib, unda integratsiyaning yuqori va pastki chegaralari o'rnatiladi. Shaklni bog'laydigan chiziqlarni belgilovchi iboralar D, biz allaqachon yaqinlashayotgan odatiy aniq integrallar uchun integrallash chegaralari bo'ladi.

Ikkilamchi integralni iteratsiyaga keltirish

To'rtburchak maydon qutisi

Bunday funktsiya qo'sh integralga ega bo'lsin

Kimga ushbu qo'sh integralni hisoblang , uni formaga ega bo'lgan takrorlangan integralga kamaytirishingiz kerak

Avval ichki (o'ng) aniq integralni, keyin tashqi (chap) aniq integralni hisoblashingiz kerak.

Siz rollarni almashtirishingiz mumkin x Va y

1-misol Ikki tomonlama integralni hisoblash

Biz y doimiyligini hisobga olib, ichki (o'ng) integralni hisoblaymiz. Qabul qilamiz.

2-misol Ikki tomonlama integralni hisoblash

Yechim. Ushbu qo'sh integralni takrorlangan integralga keltiramiz

Chizma bo'yicha biz integratsiya maydonini quramiz:

Endi biz tashqi (chap) integralni faqat hisoblangan ichki (o'ng) integraldan hisoblaymiz:

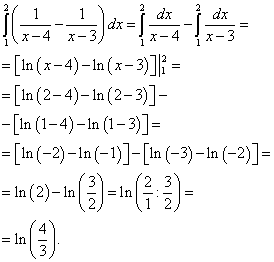
Natijada ushbu qo'sh integralning yechimi bo'ladi.

Ikki tomonlama integralni o'zingiz hisoblang va keyin yechimni ko'ring

Egri chiziqli yoki uchburchak mintaqa holati

Yana ikkita o'zgaruvchili funksiya berilsin f(x, y) , va cheklovlar D: biroz boshqacha ko'rinishga ega:

Ushbu yozuv raqam degan ma'noni anglatadi D to'g'ri chiziqli mintaqada bo'lgani kabi, chap va o'ngdagi chegara - to'g'ri chiziqlar x = a Va x = b, lekin pastda va yuqorida tenglamalar bilan berilgan egri chiziqlar va. Boshqacha qilib aytganda, va funksiyalar.

Bunday funksiya ham qo'sh integralga ega bo'lsin

Ushbu qo'sh integralni hisoblash uchun uni shaklga ega bo'lgan takrorlangan integralga keltirishimiz kerak.

Bu erda integratsiya chegaralari a Va b raqamlar va va funksiyalardir. Uchburchak mintaqada funktsiyalardan biri yoki to'g'ri chiziq tenglamasidir. Bu holat 3-misolda muhokama qilinadi.

To'g'ri chiziqli mintaqada bo'lgani kabi, siz avval o'ng aniq integralni, keyin chap aniq integralni hisoblashingiz kerak.

Xuddi shu tarzda siz rollarni almashtirishingiz mumkin. x Va y. Keyin takrorlangan integral ko'rinishga ega bo'ladi

Bunday takrorlangan integral aynan shunday echilishi kerak: birinchi navbatda ichki (o'ng) integral, keyin tashqi (chap).

5-misol Ikki tomonlama integralni hisoblash

Yechim. Ushbu qo'sh integralni takrorlangan integralga keltiramiz

Chizmada biz integratsiya maydonini quramiz va uning uchburchak ekanligini ko'ramiz:

X ni doimiy deb hisoblab, ichki (o'ng) integralni hisoblaymiz. Qabul qilamiz.

Endi biz faqat hisoblangan ichki (o'ng) integralning tashqi (chap) integralini hisoblaymiz. Birinchidan, biz bu integralni integrallar yig'indisi sifatida ifodalaymiz:

Birinchi muddatni hisoblaymiz:

Ikkinchi muddatni hisoblaymiz:

Uchinchi muddatni hisoblaymiz:

Ushbu qo'sh integralning yechimi bo'lgan yig'indini olamiz:

6-misol Ikki tomonlama integralni hisoblash

Yechim. Ushbu qo'sh integralni takrorlangan integralga keltiramiz

Chizma bo'yicha biz integratsiya maydonini quramiz:

X ni doimiy deb hisoblab, ichki (o'ng) integralni hisoblaymiz. Qabul qilamiz.

Endi biz tashqi (chap) integralni faqat hisoblangan ichki (o'ng) integraldan hisoblaymiz:

Natijada ushbu qo'sh integralning yechimi bo'ladi.

x- to'g'ri va noto'g'ri y-to'g'ri va noto'g'ri integratsiya domenlari

Ikkilamchi integralning integrallash sohasi shunday chiziqlar bilan chegaralanganki, integratsiya sohasini qismlarga bo'lish va har bir mos keladigan takrorlangan integralni alohida yechish kerak bo'ladi. Bular quyidagi holatlardir:

1) integratsiya maydoni - pastki yoki yuqori (chap yoki o'ng) chegara ko'rinishidagi ikki yoki undan ortiq to'g'ri yoki egri chiziqlarga ega bo'lgan rasm;

2) integratsiya maydoni - bu chiziqlar ikki nuqtadan ko'proq kesishadigan raqam.

Agar yuqorida aytilganlar integratsiya mintaqasining chap yoki o'ng chegarasiga tegishli bo'lsa, ya'ni chegaralar orqali ifodalangan chiziqlar bilan berilgan cheklovlar. x, keyin integratsiya sohasi chaqiriladi x- noto'g'ri. To'g'ri chiziq bo'lsa y = y0 tegishli chegarani faqat bitta nuqtada kesib o'tadi va agar chegara vazifasini faqat bitta chiziq yoki egri chiziq bo'lsa, u holda integratsiya mintaqasi deyiladi. x-to'g'ri

Xuddi shunday, chegara bilan ifodalangan chiziqlar bilan belgilangan bo'lsa y, Streyt x = x0 bir nechta nuqtada kesishsa yoki bir nechta chiziq yoki egri chiziq chegara bo'lib xizmat qilsa, u holda integratsiya maydoni deyiladi. y- noto'g'ri. Endi belgilarni keltiring y-to'g'ri maydon, ehtimol, juda oddiy.

Hozirgacha biz misollarni ko'rib chiqdik x- noto'g'ri va y-muntazam integratsiya sohalari. Endi to'g'rilik sharti buzilgan holatlarni ko'rib chiqing.

7-misol Integratsiya maydoni chiziqlar bilan chegaralangan qo'sh integralni hisoblang y = x , xy = 1 , y = 2 .

Yechim. Integratsiya sohasi y-noto'g'ri, chunki uning pastki chegarasini bitta chiziq bilan o'rnatib bo'lmaydi y = y(x) . Yuqoridagi rasmda ko'rib turganingizdek, pastki chegara quyidagilardan iborat y = x(qora jigarrang) va xy= 1 (yashil). Shuning uchun to'g'ridan-to'g'ri x= 1 (qora) biz integratsiya maydonini ikki qismga bo'lishimiz mumkin - va .

Bu ikki tomonlama integral quyidagicha hisoblanadi:

Integratsiya tartibini o'zgartirish

Yuqorida ta'kidlab o'tilganidek, qo'sh integralni takrorlangan integralga qisqartirgandan so'ng, o'zgaruvchilarni o'zgartirish mumkin x Va y rollar, yoki, boshqacha qilib aytganda, integratsiya tartibini o'zgartirish.

Integratsiya tartibining o'zgarishini O "Genrining quyidagi so'zlari bilan majoziy ravishda tasvirlash mumkin: "O'rmon aholisi o'zini shunday tutadi - qafasga tushgan hayvon va qafasda yashovchi o'zini shunday tutadi. - shubhalar o'rmonida yo'qolgan odam." Natija, shuningdek, Genrining so'zlariga ko'ra, bitta va bir xil: "Chalmers maktubni minglab mayda bo'laklarga bo'lib tashladi va uning qimmat gilamini azoblay boshladi, uni orqaga o'tkazdi va oldinga." ( O.Genri. Madison maydonidan Shehrazade.)

Keyin, agar o'zgaruvchining ustida chap integralga ega bo'lsak x, va o'ng y, keyin integratsiya tartibini o'zgartirgandan so'ng, hamma narsa aksincha bo'ladi. Keyin "yangi" y uchun integratsiya chegaralari "eski" x dan "qarz" olinishi kerak va "yangi" x uchun integratsiya chegaralari shaklda olinishi kerak. teskari funktsiya, y uchun chegarani belgilovchi x ga nisbatan tenglamani yechish.

8-misol

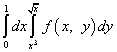Yechim. Integrallash tartibini o'zgartirgandan so'ng, y ustidagi integral chapga, x ga nisbatan integral esa o'ngga aylanadi. Biz "yangi" o'yinchi uchun integratsiya chegaralarini "eski" X dan qarzga olamiz, ya'ni pastki chegara nolga, yuqori chegara esa bittaga teng. "Eski" o'yinchi uchun integratsiya chegaralari va tenglamalar bilan berilgan. Ushbu tenglamalarni x ga nisbatan yechib, biz x uchun yangi integratsiya chegaralarini olamiz:

(pastki) va (yuqori).

Shunday qilib, integrallash tartibini o'zgartirgandan so'ng, takrorlangan integral quyidagicha yoziladi:

Qo'sh integralda integratsiya tartibini o'zgartirgandan so'ng, integratsiya sohasi ko'pincha aylanadi y- noto'g'ri yoki x- noto'g'ri (oldingi xatboshiga qarang). Keyin integrallash mintaqasini qismlarga bo'lish va har bir mos keladigan takrorlangan integralni alohida yechish talab qilinadi.

Integratsiya sohasining qismlarga bo'linishi ko'plab talabalar uchun ma'lum qiyinchiliklarni keltirib chiqarganligi sababli, biz avvalgi xatboshida keltirilgan misol bilan cheklanmaymiz, lekin yana bir nechta misollarni tahlil qilamiz.

9-misol Takrorlangan integral uchun integrallash tartibini o'zgartiring

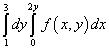Yechim. Shunday qilib, bu takrorlangan integralning integrallash maydoni to'g'ri chiziqlar bilan cheklangan y = 1 , y = 3 , x = 0 , x = 2y .

Boshqa tartibda integratsiyalashganda, mintaqaning pastki chegarasi ikkita to'g'ri chiziqdan iborat: AB Va Miloddan avvalgi, ular tenglamalar bilan berilgan y= 1 va y = x/2 , buni quyidagi rasmda ko'rish mumkin.

Bunday noaniqlikdan chiqish yo'li integratsiya sohasini ikki qismga bo'lishdir. Integratsiya maydoni to'g'ri chiziq bilan bo'linadi BM. Yangi integratsiya chegaralari teskari funktsiyani topish yo'li bilan hisoblanadi. Ushbu yechimga ko'ra, integrallash tartibini o'zgartirgandan keyin takrorlangan integral ikkita integral yig'indisiga teng bo'ladi:

Tabiiyki, qo'sh integralning yechimi bir xil bo'ladi, bu esa ushbu misol shartida berilgan takrorlangan integralga kamayadi.

10-misol Takrorlangan integral uchun integrallash tartibini o'zgartiring

Yechim. Shunday qilib, takrorlangan integralning integrallash maydoni to'g'ri chiziqlar bilan cheklangan x = 0 , x= 2 va egri chiziqlar va.

Quyidagi rasmda ko'rinib turibdiki, o'qga parallel to'g'ri chiziq 0x, integratsiya mintaqasining pastki chegarasini ikki nuqtadan ortiq kesib o'tadi.

Shuning uchun biz integratsiya sohasini rasmda qora rangda chizilgan to'g'ri chiziqlar orqali uch qismga ajratamiz. Yangi integratsiya chegaralari teskari funktsiyani topish yo'li bilan hisoblanadi. Integratsiyaning uchta yangi sohalari uchun chegaralar quyidagicha bo'ladi.

Ushbu yechimga ko'ra, integrallash tartibini o'zgartirgandan keyin takrorlangan integral uchta integral yig'indisiga teng bo'ladi:

Uchta integralning bir xil yig'indisi qo'sh integralga teng bo'ladi, bu misol shartida berilgan takrorlangan integralga kamayadi.

Va shunga qaramay, fors-major holatlari ko'pincha talabalarga avvalgi bosqichda - integratsiya chegaralarini belgilashda xalaqit beradi. Xavotir va chalkashlik hech qanday asosga ega emas: agar odatda integratsiya sohasini qismlarga bo'lish uchun chizmaga qarash va takrorlangan integral - integrallar jadvalini echish uchun etarli bo'lsa, unda chegaralarni belgilashda ba'zi o'quv tajribasi kerak bo'ladi. integratsiya. Keling, bir misolni ko'rib chiqaylik, unda biz faqat integratsiya chegaralarini tartibga solish va deyarli avtomatik ravishda mintaqaning bo'linishi haqida to'xtalib, yechimning o'zini tashlab qo'yamiz.

11-misol. Qo'sh integralning integrallash chegaralarini toping, agar integrallash sohasi bo'lsa D quyidagicha o'rnating:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Yechim. aniq (orqali x Va y"ifloslarsiz") integratsiya maydonini cheklovchi chiziqlar ko'rsatilmagan. X uchun ular ko'pincha y orqali ifodalangan yuqori va pastki chegaralarga bir nuqtada tegib turadigan to'g'ri chiziqlar bo'lib chiqadi, shuning uchun biz aynan shu yo'ldan boramiz. Bundan tashqari, integratsiya tartibini o'zgartirganda, biz bir xil maydonga ega bo'lgan integratsiya maydonini olamiz. Keling, o'yinchi uchun tengsizliklarni yechib, olamiz:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Olingan chiziqlarni chizilgan ustiga quramiz. X ga nisbatan integratsiya chegaralari, albatta, chiziqlardir x= 0 va x= 2 . Ammo integratsiya mintaqasi bo'lib chiqdi y-noto'g'ri, chunki uning yuqori chegarasini bitta chiziq bilan o'rnatib bo'lmaydi y = y(x) .

O'qish foydali bo'lishi mumkin: