Eckpunkte eines Trapezes. Material zur Geometrie zum Thema „Trapez und seine Eigenschaften“. Eigenschaften eines gleichschenkligen Trapezes
G.I. Kovaleva
METHODE ZUR UNTERSUCHUNG DER EIGENSCHAFTEN DES TRAPEZES
In den Materialien verschiedener Tests und Prüfungen stößt man sehr häufig auf Trapezaufgaben, deren Lösung von den Studierenden die Kenntnis der „nichtprogrammierten“ Eigenschaften des Trapezes erfordert. (Eigenschaften gelten als Mittellinie Trapez, Eigenschaften von Diagonalen und Winkeln eines gleichschenkligen Trapezes.) Welche bemerkenswerten Eigenschaften hat ein Trapez? Wo und wann kann man sie in einem Schulgeometriekurs studieren?
Methode zur Untersuchung der Eigenschaften eines Trapezes
Nachdem wir nun mehrere Typen gesehen haben, wollen wir uns mit Formen befassen, die nicht die Eigenschaften von Parallelogrammen haben. Denken Sie daran, dass Parallelogramme Vierecke sind, deren gegenüberliegende Seiten parallel sind. In diesem Abschnitt betrachten wir Vierecke, deren gegenüberliegende Seiten sich irgendwann schneiden können. Beginnen wir unsere Erkundung mit der Untersuchung einiger Eigenschaften von Trapezen. Definition. Ein Trapez ist ein Viereck mit genau einem Paar paralleler Seiten.
Nachdem wir die Eigenschaften der Mittellinie eines Trapezes untersucht haben, können wir sie formulieren und beweisen Eigenschaft eines Segments, das die Mittelpunkte der Diagonalen eines Trapezes verbindet. Die Strecke, die die Mittelpunkte der Diagonalen eines Trapezes verbindet, ist gleich der halben Basisdifferenz.
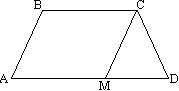
Beim Üben der Haupttechnik zur Lösung von Problemen auf dem Trapez „Zeichne zwei Höhen“ müssen die Schüler die Aufgabe anbieten: „Lassen Sie BT- Höhe gleichschenkliges Trapez A B C D mit Begründung Chr Und ANZEIGE.
 ,
,
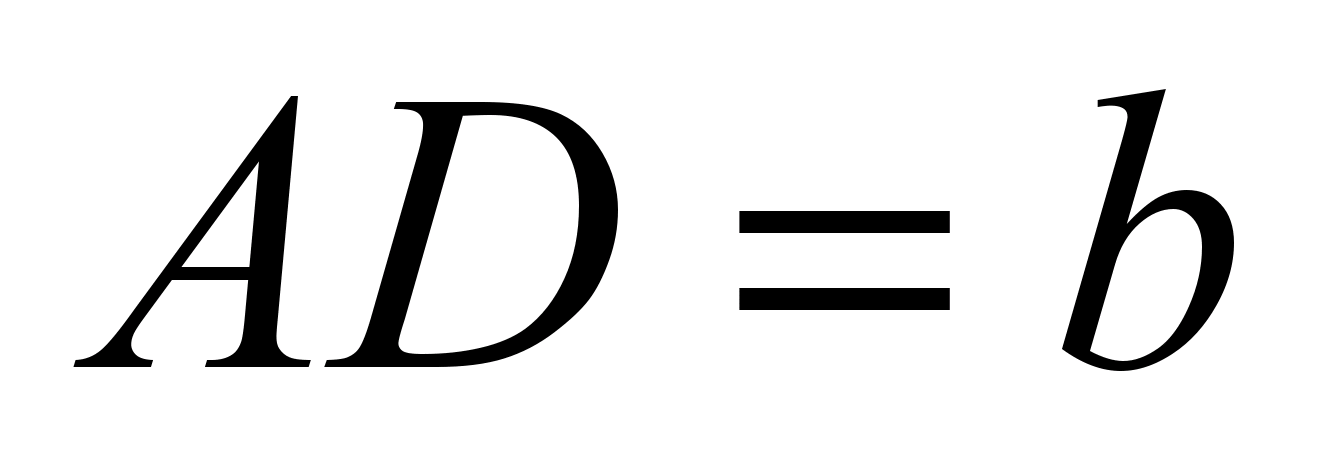 . Finden Sie die Längen der Segmente BEI Und TD».
. Finden Sie die Längen der Segmente BEI Und TD».
„Der Einsatz der Trigonometrie zur Lösung planimetrischer Probleme“
Da ein Trapez genau ein Paar paralleler Seiten haben muss, müssen wir beweisen, dass ein Paar gegenüberliegender Seiten parallel ist und das andere nicht zu unserem. Wenn wir vergessen zu beweisen, dass ein Paar gegenüberliegender Seiten nicht parallel ist, schließen wir die Möglichkeit nicht aus, dass das Viereck ein Parallelogramm ist. Daher wird dieser Schritt für die Arbeit an den verschiedenen Übungen mit dem Trapez absolut unerlässlich sein.
Bevor wir uns direkt mit dem Studium der Trapeze befassen, müssen wir die Namen der verschiedenen Teile dieser Vierecke kennen, um ihre Seiten und Winkel genau bestimmen zu können. Alle Trapeze bestehen aus zwei Hauptteilen: der Basis und den Beinen. Gegenüberliegende Seiten eines Trapezes, die zueinander parallel sind, werden als Basen bezeichnet. Die anderen Seiten des Trapezes, die sich irgendwann schneiden, wenn sie gestreckt sind, werden als Beine des Trapezes bezeichnet.
Das Thema „Ähnlichkeit von Figuren“ ist sehr nützlich, um die Eigenschaften eines Trapezes zu untersuchen. Beispielsweise teilen die Diagonalen eines Trapezes es in vier Dreiecke, und die an die Grundflächen angrenzenden Dreiecke sind ähnlich und die an den Seiten angrenzenden Dreiecke sind gleich. Nennen wir diese Aussage MitEigenschaft von Dreiecken, in die ein Trapez durch seine Diagonalen zerlegt wird. Darüber hinaus lässt sich der erste Teil der Behauptung sehr leicht durch das Ähnlichkeitszeichen von Dreiecken in zwei Winkeln beweisen. Der zweite Teil kann den Studierenden in Form einer Aufgabe angeboten werden.
Ähnlichkeit geformter trapezförmiger Dreiecke
Die Ober- und Unterseite des Trapezes verlaufen parallel zueinander, sind also die Basis des Trapezes. Die anderen Seiten des Trapezes schneiden sich, wenn sie gestreckt sind, sie sind also die Schenkel des Trapezes. Das Segment, das die Mittelpunkte der Schenkel des Trapezes verbindet, wird Mittelsegment genannt. Die Länge dieses Segments ist immer gleich der Hälfte der Summe der Trapezgrundflächen bzw.
Das Verhältnis der Längen von Segmenten und Basen
Die Abmessung des Mittelsegments hängt nur von der Länge der Trapezbasen ab. Es gibt jedoch eine wichtiges Merkmal dass manche Trapeze ausschließlich von ihren Beinen abhängig sind. Schauen wir uns nun diese Trapeze an. Ein gleichschenkliges Trapez ist ein Trapez, dessen Beine deckungsgleich sind. Wenn ein Viereck genau ein Paar paralleler Linien hat, dann ist das Viereck per Definition ein Trapez. Die Definition eines gleichschenkligen Trapezes fügt eine weitere Spezifikation hinzu: Die Schenkel des Trapezes müssen deckungsgleich sein.
Ebenso Dreiecke
BOC Und AOB haben eine gemeinsame Höhe, wenn wir Segmente als Basis nehmen CO Und OA.
Dann 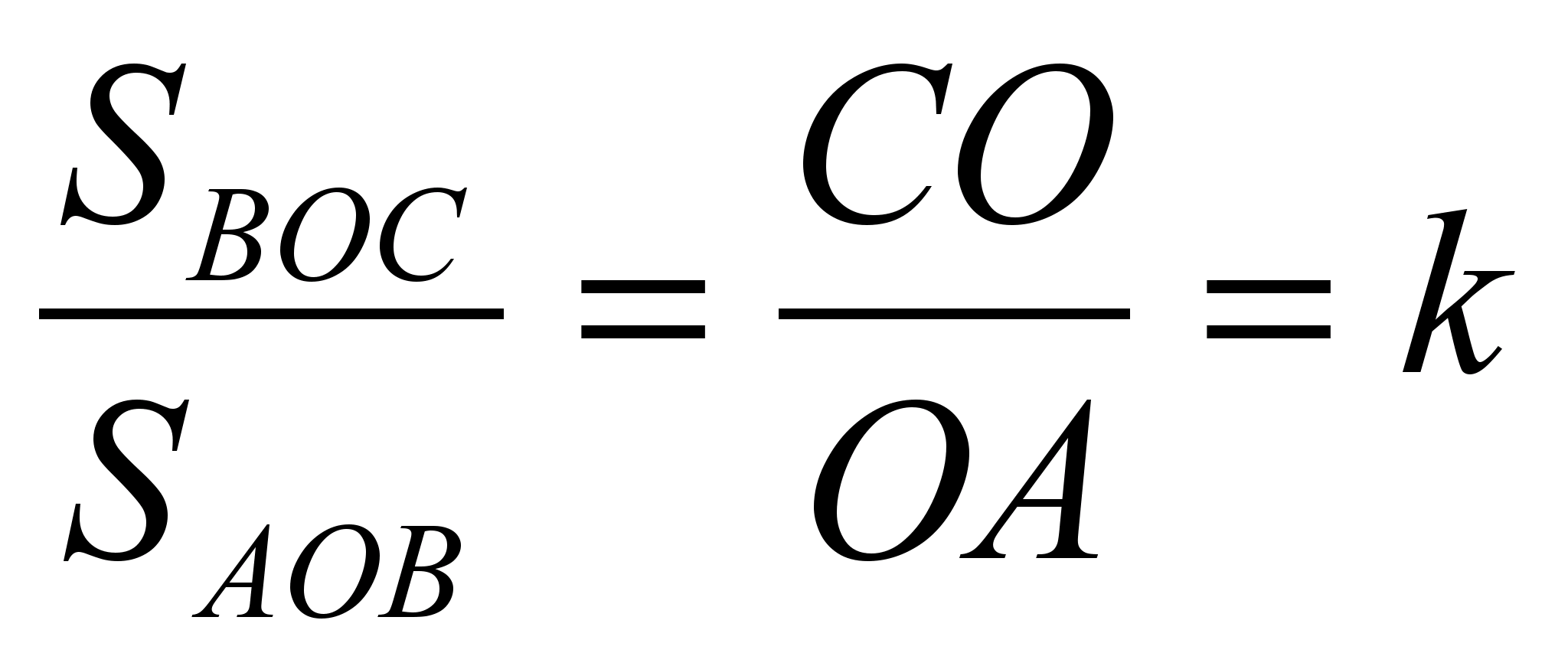 Und
Und 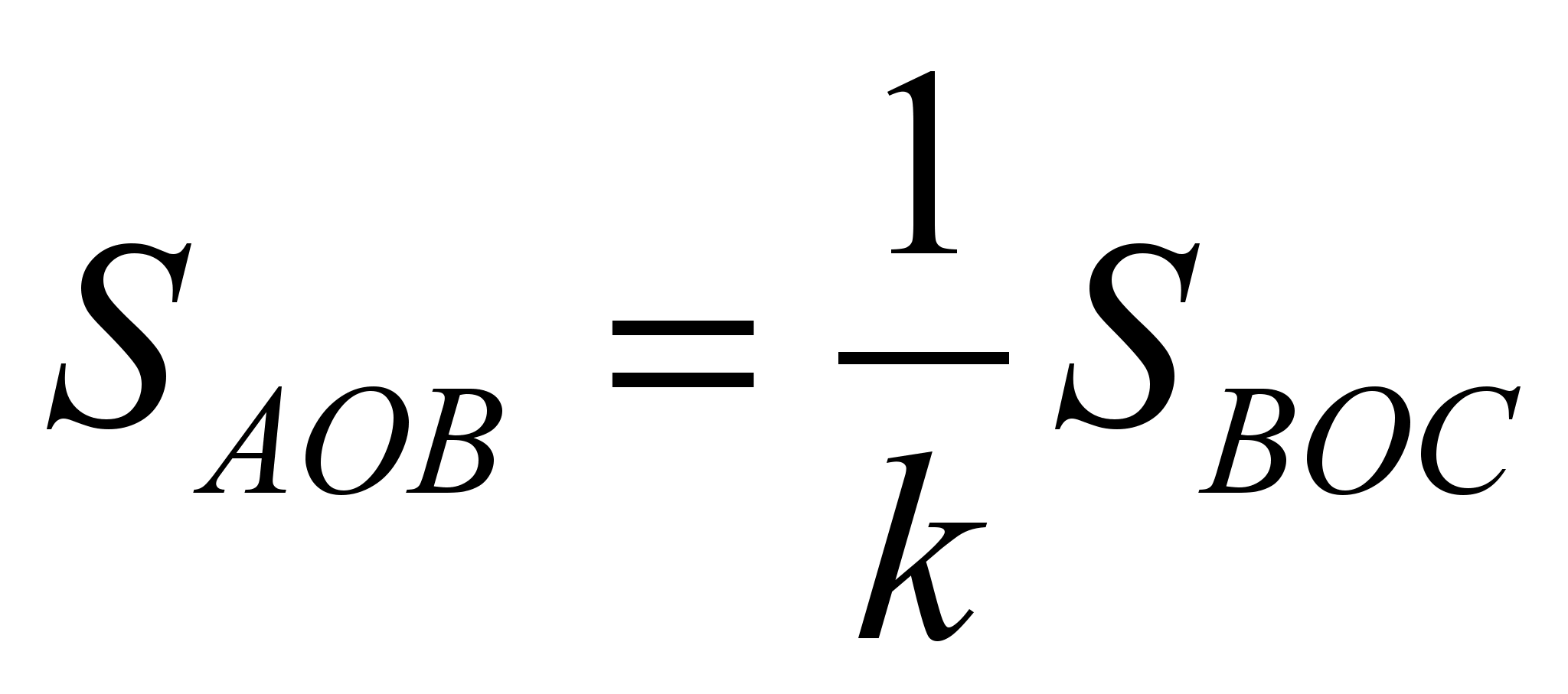 .
.
Aus diesen beiden Thesen folgt, dass 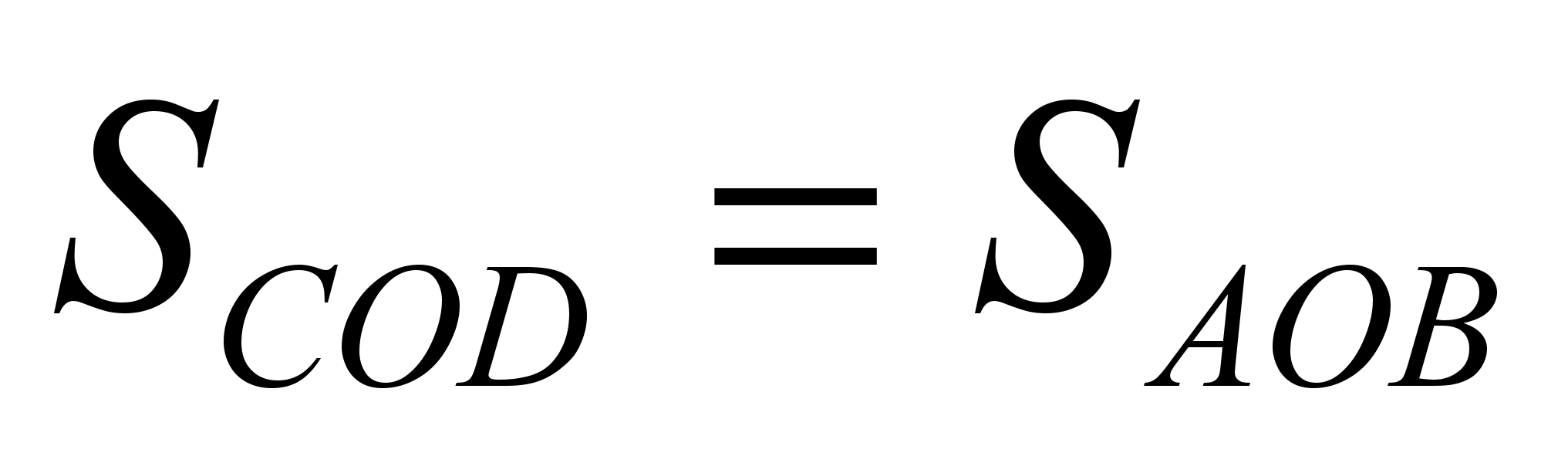 .
.
Es gibt mehrere Theoreme, mit denen wir beweisen können, dass ein Trapez gleichschenklig ist. Diese Eigenschaften sind unten aufgeführt. Ein Trapez ist genau dann gleichschenklig, wenn die Grundwinkel übereinstimmen. Ein Trapez ist genau dann gleichschenklig, wenn die Diagonalen deckungsgleich sind.
Wenn ein Trapez gleichschenklig ist, dann sind seine entgegengesetzten Winkel komplementär. Ein Drachen ist ein Viereck mit zwei verschiedenen Paaren benachbarter Seiten, die kongruent sind. Denken Sie daran, dass Parallelogramme auch Paare kongruenter Seiten hatten. Ihre kongruenten Seiten waren jedoch immer entgegengesetzt. Drachen haben zwei Paare kongruenter Seiten, die sich an zwei verschiedenen Punkten treffen. Schauen wir uns die Abbildung unten an, um zu verstehen, wie ein Drachen aussieht.
Es wäre toll, sich nicht auf die formulierte Aussage einzulassen, sondern sie zu finden die Beziehung zwischen den Flächen der Dreiecke, in die ein Trapez durch seine Diagonalen unterteilt wird
, und fordert die Schüler auf, das Problem zu lösen: „O sei der Schnittpunkt der Diagonalen des Trapezes A B C D mit Begründung Chr Und ANZEIGE. Es ist bekannt, dass die Flächen von Dreiecken BOC Und AOD jeweils gleich  Und
Und 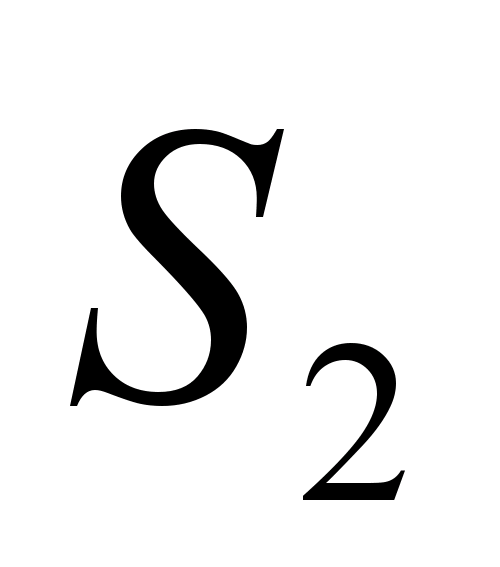 . Finden Sie die Fläche des Trapezes.
. Finden Sie die Fläche des Trapezes.
Drachen haben mehrere Eigenschaften, die uns helfen, sie von anderen Quads zu unterscheiden. Die Diagonalen des Drachens treffen im rechten Winkel aufeinander. Drachen haben genau ein Paar entgegengesetzter Winkel, die kongruent sind. Diese beiden Eigenschaften werden im folgenden Diagramm veranschaulicht.
Das ist unser einziges kongruentes Winkelpaar, denn? Lassen Sie die Übung einige der Probleme lösen, die die Nutzung der Eigenschaften von Trapezen und Drachen erfordern, die wir gerade kennengelernt haben. Da uns die Längen der Grundflächen des Trapezes bekannt sind, können wir die Länge des mittleren Segments ermitteln. Um dies herauszufinden, verwenden wir die Formel, die wir für das mittlere Segment angegeben haben.
Als . Daher aus der Ähnlichkeit von Dreiecken BUMC Und AOD folgt dem 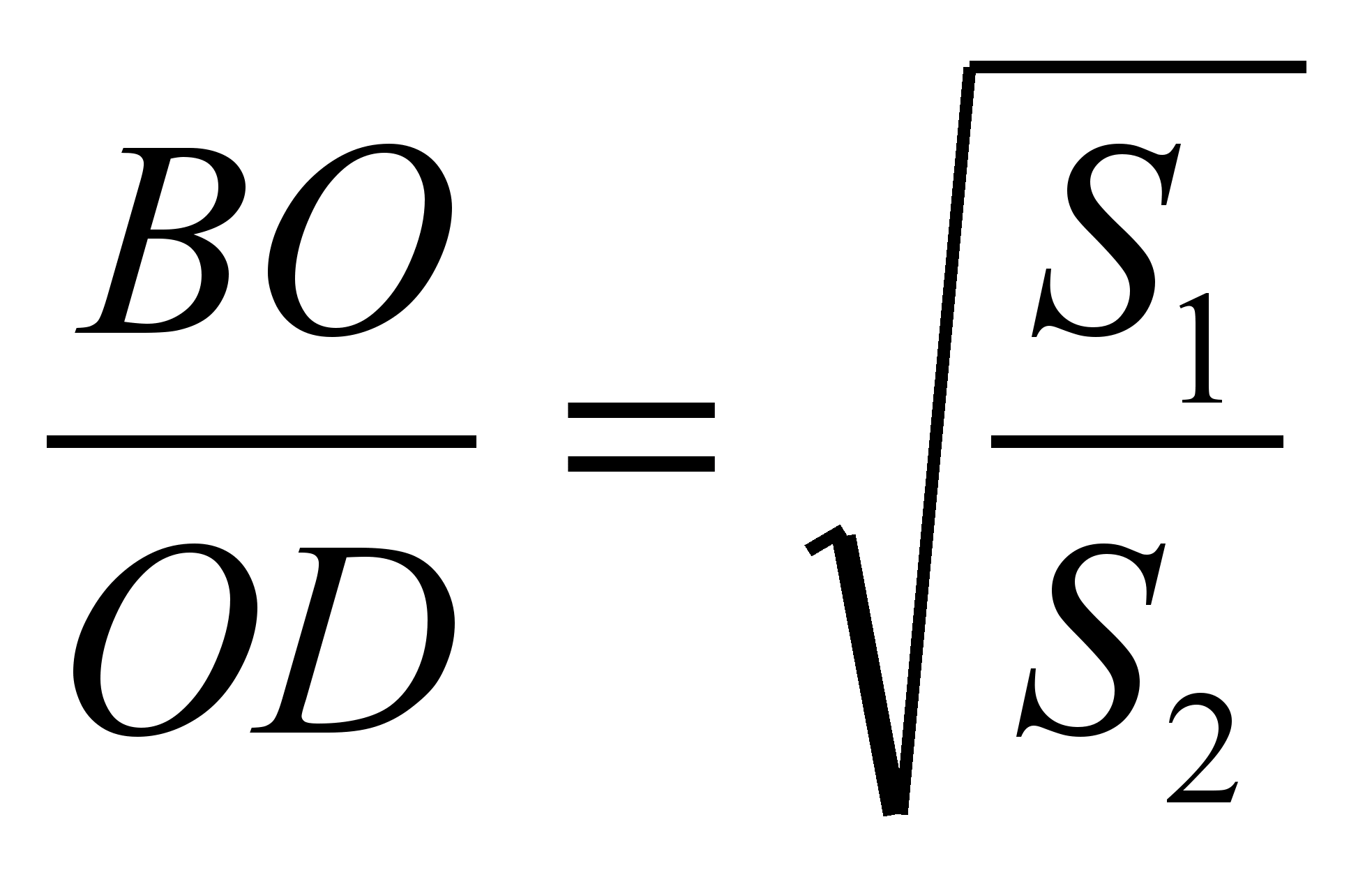 .Somit,
.Somit, 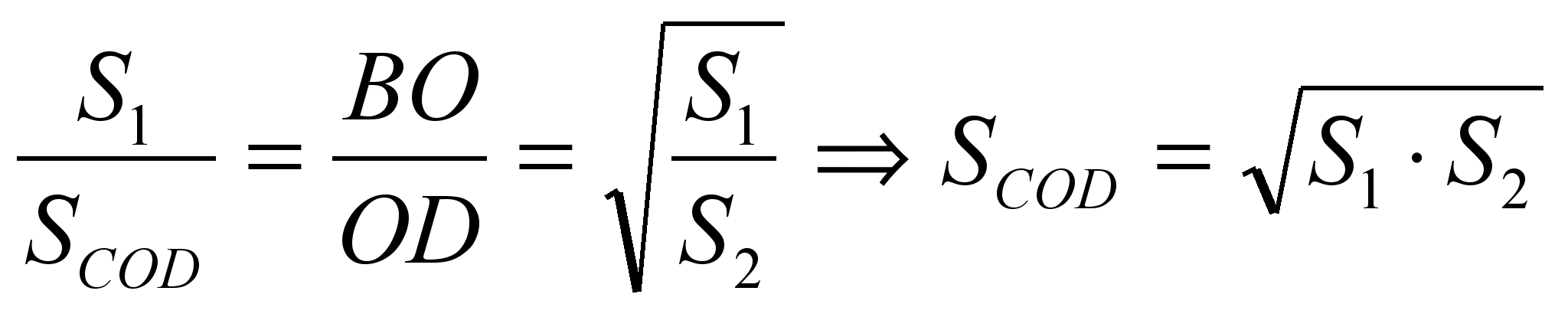 . Dann
. Dann
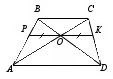
Mit Hilfe der Ähnlichkeit kann man auch beweisen Eigenschaft eines Segments, das durch den Schnittpunkt der Diagonalen eines Trapezes parallel zu den Basen verläuft. Wir laden die Schüler ein, das Problem zu lösen: „O sei der Schnittpunkt der Diagonalen des Trapezes.“ A B C D mit Begründung Chr Und ANZEIGE. , . Finden Sie die Länge des Segments PK durch den Schnittpunkt der Diagonalen des Trapezes parallel zu den Basen verlaufen. In welche Segmente ist es unterteilt? PK Punkt UM».
In der Abbildung wurde uns nur das Maß eines Winkels angegeben, daher sollten wir in der Lage sein, auf der Grundlage dieses einen Elements weitere Informationen abzuleiten. Da das Viereck ein gleichschenkliges Trapez ist, wissen wir, dass die Grundwinkel übereinstimmen. Nun wollen wir herausfinden, wie viel?
Zusammen ergeben sie insgesamt 128°. Erinnern Sie sich an den Polygon-Innenwinkelsatz, dass die Innenwinkel eines Vierecks 360° betragen müssen. Versuchen wir also, dies so zu nutzen, dass es uns bei der Definition einer Kennzahl hilft? Lassen Sie uns zunächst alle Winkel zusammenfassen und auf 360° einstellen.
Von hier 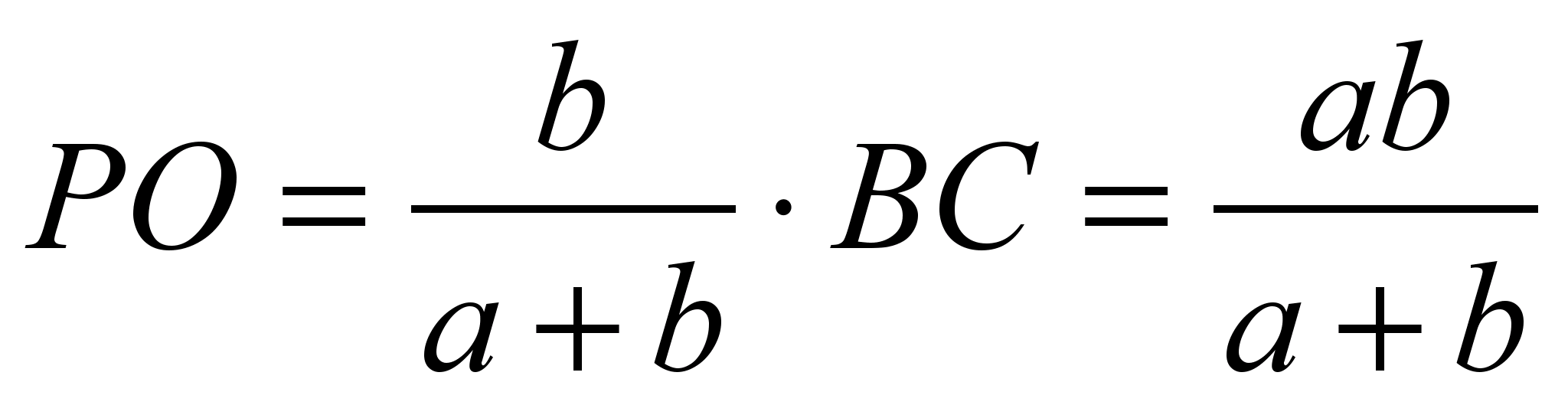 .
.
Ebenso aus der Ähnlichkeit von Dreiecken D.O.K. Und DBC, folgt daraus 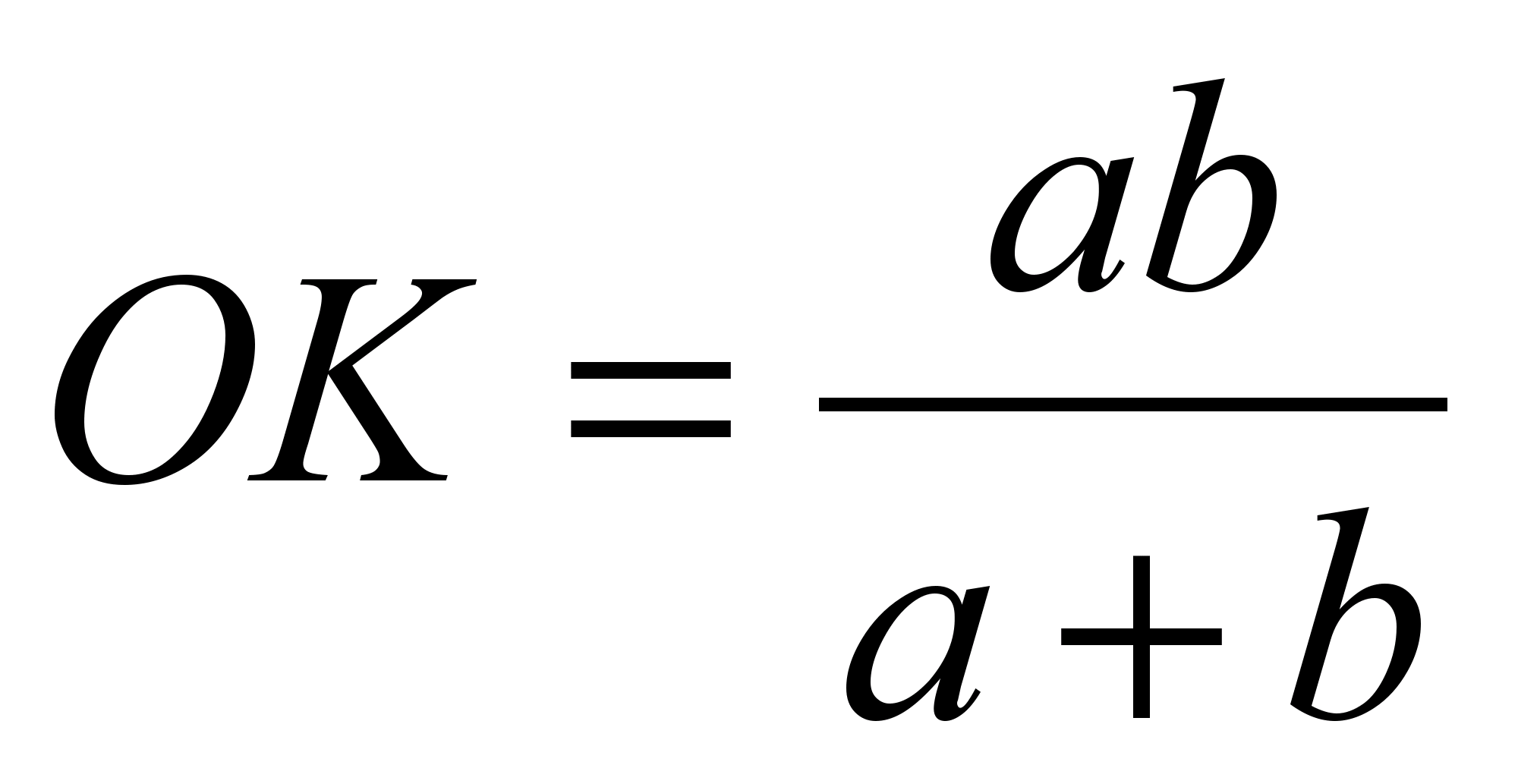 . Von hier
. Von hier 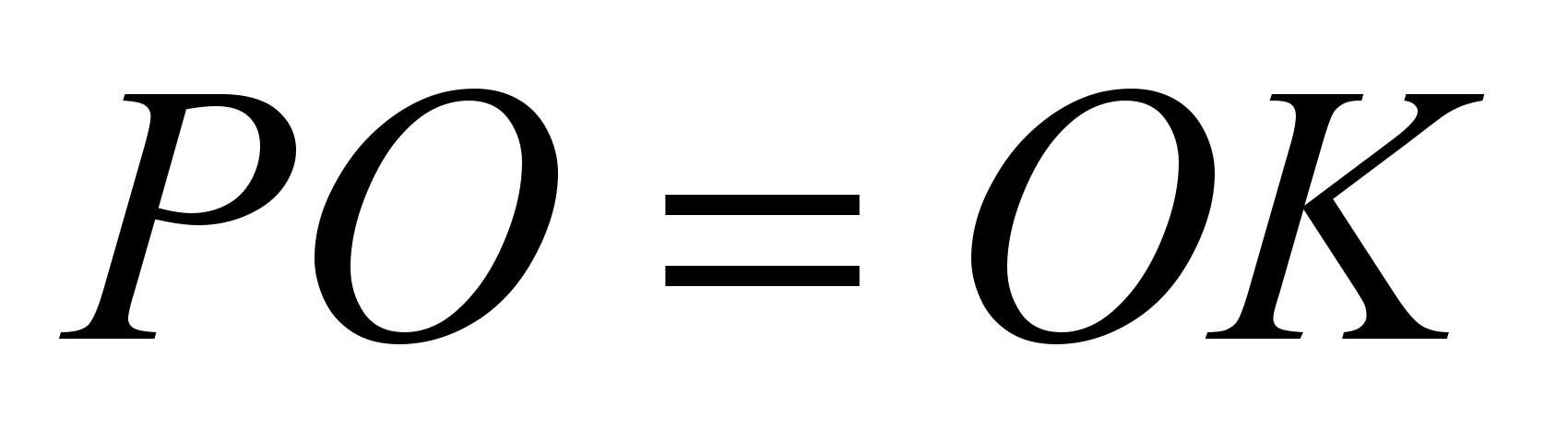 Und
Und 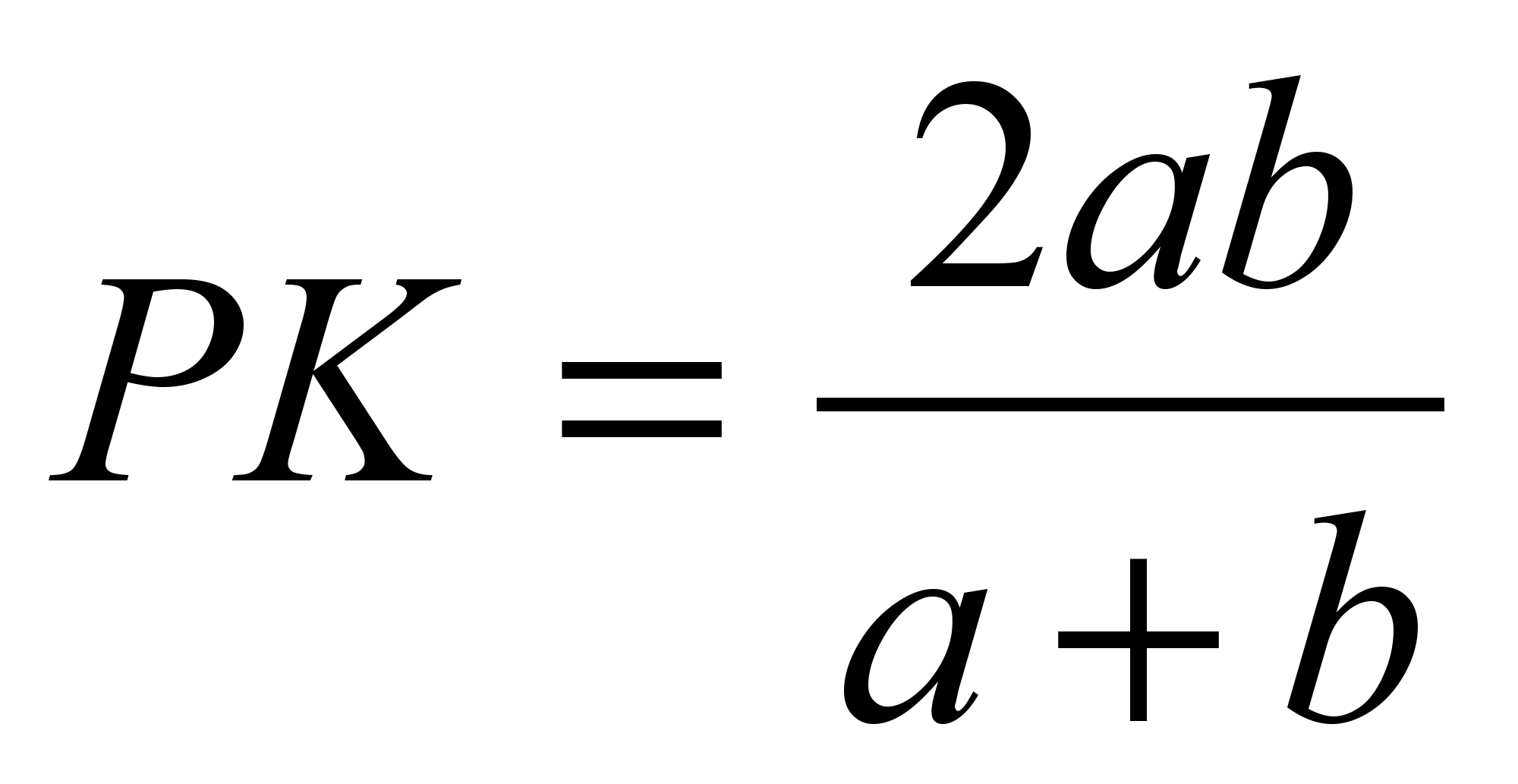 .
.
Von einem Trapez umschrieben
Wenn wir also Maßnahmen definieren? Dieser Wert bedeutet, dass die Maßnahme? Schließlich können wir 116 so einstellen, dass es dem in gezeigten Ausdruck entspricht. Obwohl die obige Methode eine tiefgreifende Möglichkeit zur Lösung der Aufgabe war, könnten wir einfach die Eigenschaft nutzen, dass die komplementären Winkel gleichschenkliger Trapeze komplementär sind. Die Lösung auf diese Weise ist viel schneller, da wir nur das 64°-Komplement finden müssen.
Sobald wir an diesem Punkt unseres Problems angelangt sind, setzen wir einfach 116 auf 4 und lösen es wie zuvor. Das wurde uns auch geschenkt? In der Vergangenheit haben wir mehrere Kongruenzsätze für Dreiecke kennengelernt, die in dieser Situation angewendet werden können, wenn wir einfach eine andere Seite oder einen anderen kongruenten Winkel finden können.
Wir bringen die Schüler dazu, die bewährte Eigenschaft zu erkennen: Ein Segment parallel zur Basis des Trapezes, das durch den Schnittpunkt der Diagonalen verläuft und zwei Punkte auf den Seiten verbindet, wird durch den Schnittpunkt der Diagonalen in zwei Hälften geteilt. Seine Länge ist das harmonische Mittel der Basen des Trapezes.
Weiter von Eigenschaft von vier Punkten: Bei einem Trapez liegen der Schnittpunkt der Diagonalen, der Schnittpunkt der Fortsetzung der Seiten und die Mittelpunkte der Basen des Trapezes auf derselben Linie.
Unsere neue Illustration ist unten abgebildet. Nachfolgend finden Sie einen zweispaltigen geometrischen Beweis dieser Übung. Um auf Geometrien zuzugreifen wie. Hören Sie auf zu kämpfen und beginnen Sie noch heute mit Tausenden von kostenlosen Ressourcen zu lernen! Die Eigenschaften werden durch Links zu den entsprechenden Lektionen dargestellt. Die Lektionen sind in einer logischen Reihenfolge aufgelistet, was bedeutet, dass sich jede Lektion auf die vorherige bezieht. und bezieht sich nicht darauf. Die Liste fasst die entsprechenden Lektionen zusammen, die sich auf befinden verschiedene Seiten Diese Seite.
Diagonalen und Höhe eines Trapezes
Ein Trapez ist genau dann gleichschenklig, wenn seine Grundwinkel übereinstimmen. Ein Trapez ist genau dann gleichschenklig, wenn seine beiden Diagonalen deckungsgleich sind. Die Mittellinie eines Trapezes verläuft parallel zu seinen Basen. Die Länge der Mittellinie eines Trapezes ist halb so groß wie die Summe der Längen seiner Grundflächen. Bei einem Trapez schneidet ein Abschnitt einer Linie, der von der Mitte einer seitlichen Seite parallel zu den Basen gezogen wird, die andere Seite in deren Mittelpunkt.
Indem wir den Schülern die Ähnlichkeit von Figuren (nicht von Dreiecken) näher bringen, können wir anbieten, die Länge des Segments zu ermitteln, das das Trapez in zwei ähnliche Teile teilt.
Auf diese Weise, Ein Segment, das ein Trapez in zwei ähnliche Trapeze teilt, hat eine Länge, die dem geometrischen Mittel der Längen der Basen entspricht.
Nachdem die Formel für die Fläche eines Trapezes abgeleitet wurde, ist es sinnvoll, sie zu beweisen Eigenschaft eines Segments, das ein Trapez in zwei gleiche Flächen teilt.
Die Mittellinie eines Trapezes ist der Ort der Punkte, die von den beiden Geraden, die die Basen des Trapezes enthalten, gleich weit entfernt sind. Bei einem Trapez beträgt die Summe der Innenwinkel an den Enden der lateralen Seite 180°. Bei einem Trapez halbiert die Mittellinie jedes Liniensegment, das einen Punkt auf einer kürzeren Basis mit einem Punkt auf einer größeren Basis verbindet. Bei einem Trapez beträgt der Abstand zwischen den Mittelpunkten seiner Diagonalen die Hälfte der Längendifferenz der größeren und kürzeren Basis.
Wenn bei einem Trapez die Summe zweier gegenüberliegender Innenwinkel 180° beträgt, dann ist das Trapez gleichschenklig. Bei einem gleichschenkligen Trapez halbiert eine Linie, die durch einen diagonalen Schnittpunkt parallel zu den Basen verläuft, den Winkel zwischen den Diagonalen. Bei einem gleichschenkligen Trapez ist die laterale Seite in einem Winkel von einem der beiden gegenüberliegenden Eckpunkte aus zu sehen.
Lasst uns ein System schaffen 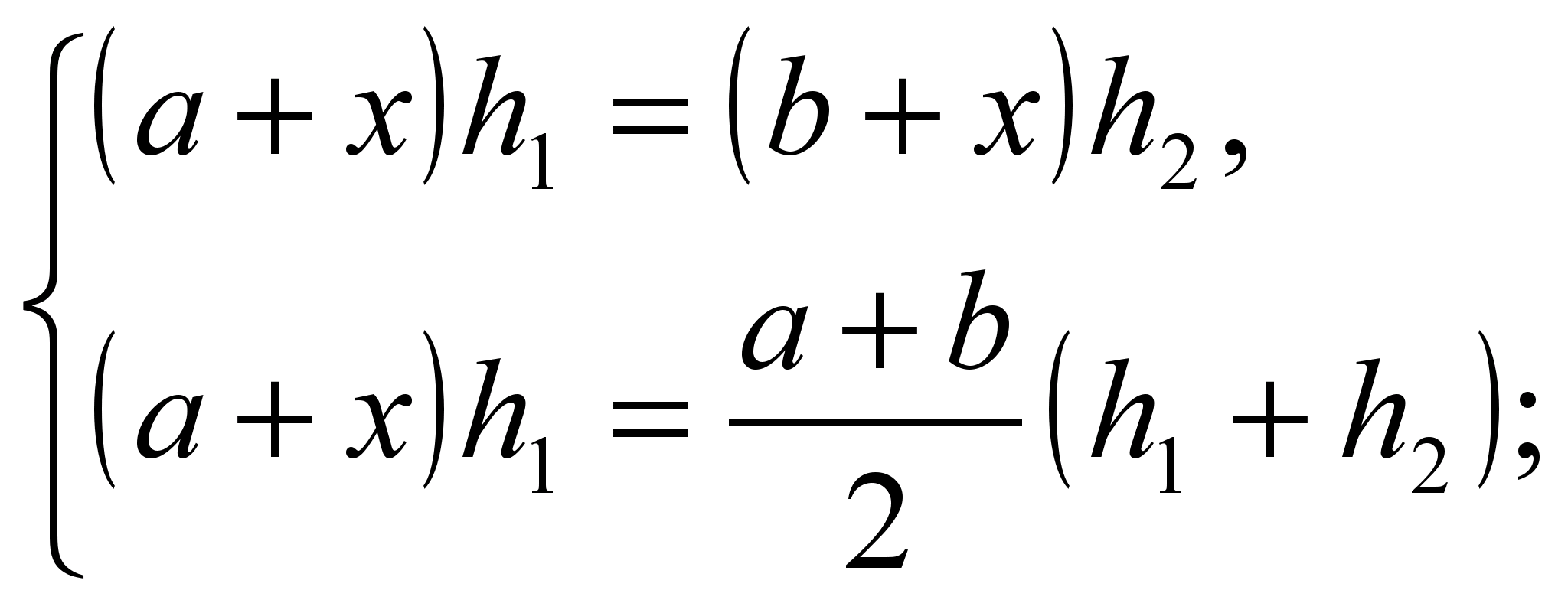
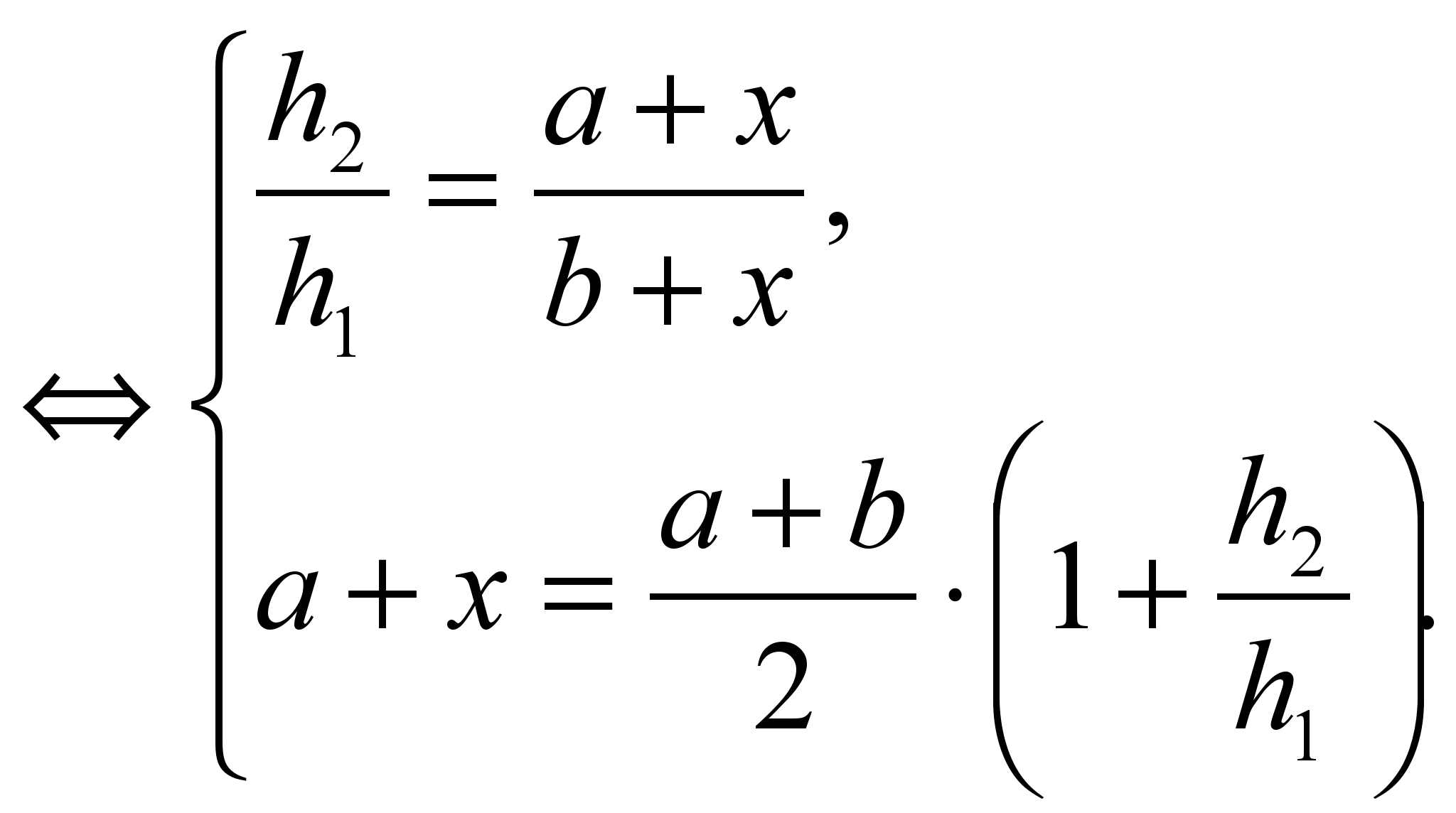
Systemlösung 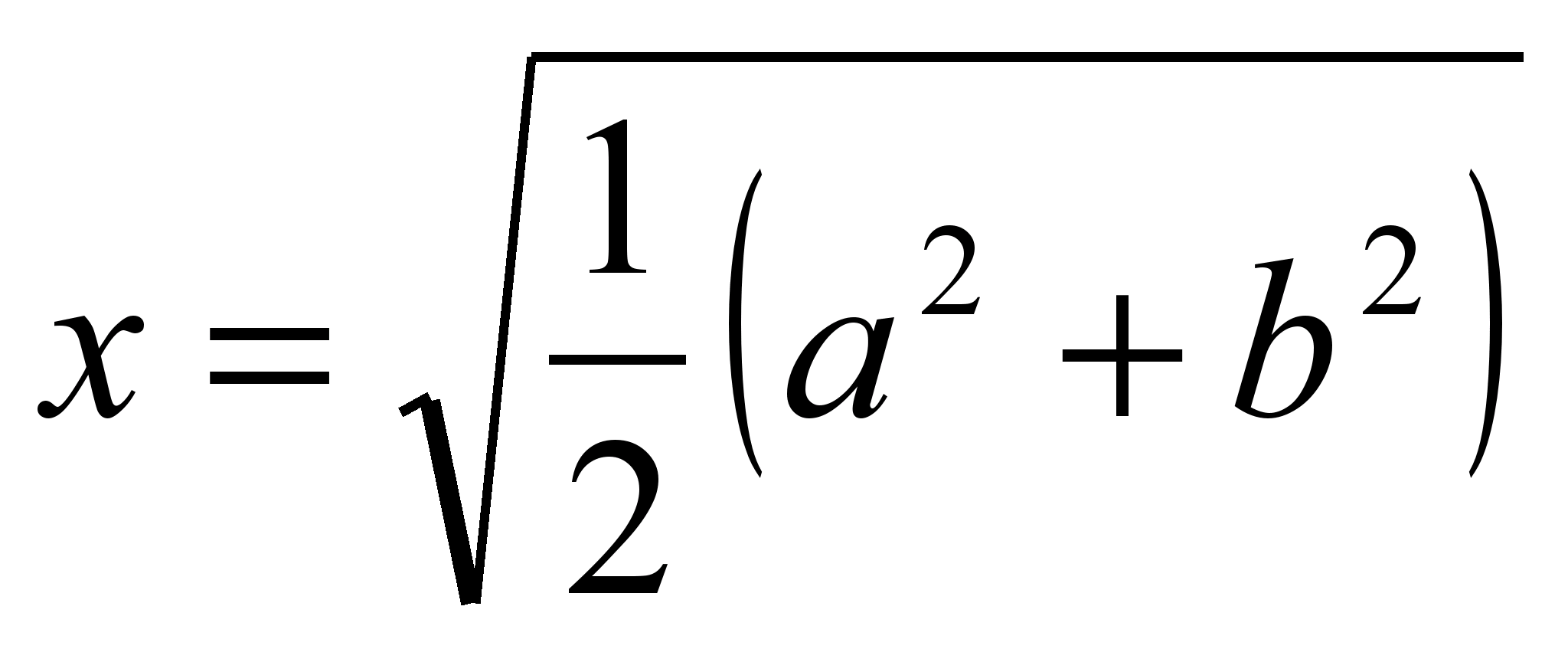 .
.
Auf diese Weise, die Länge des Segments, das das Trapez in zwei gleiche Teile teilt, ist gleich 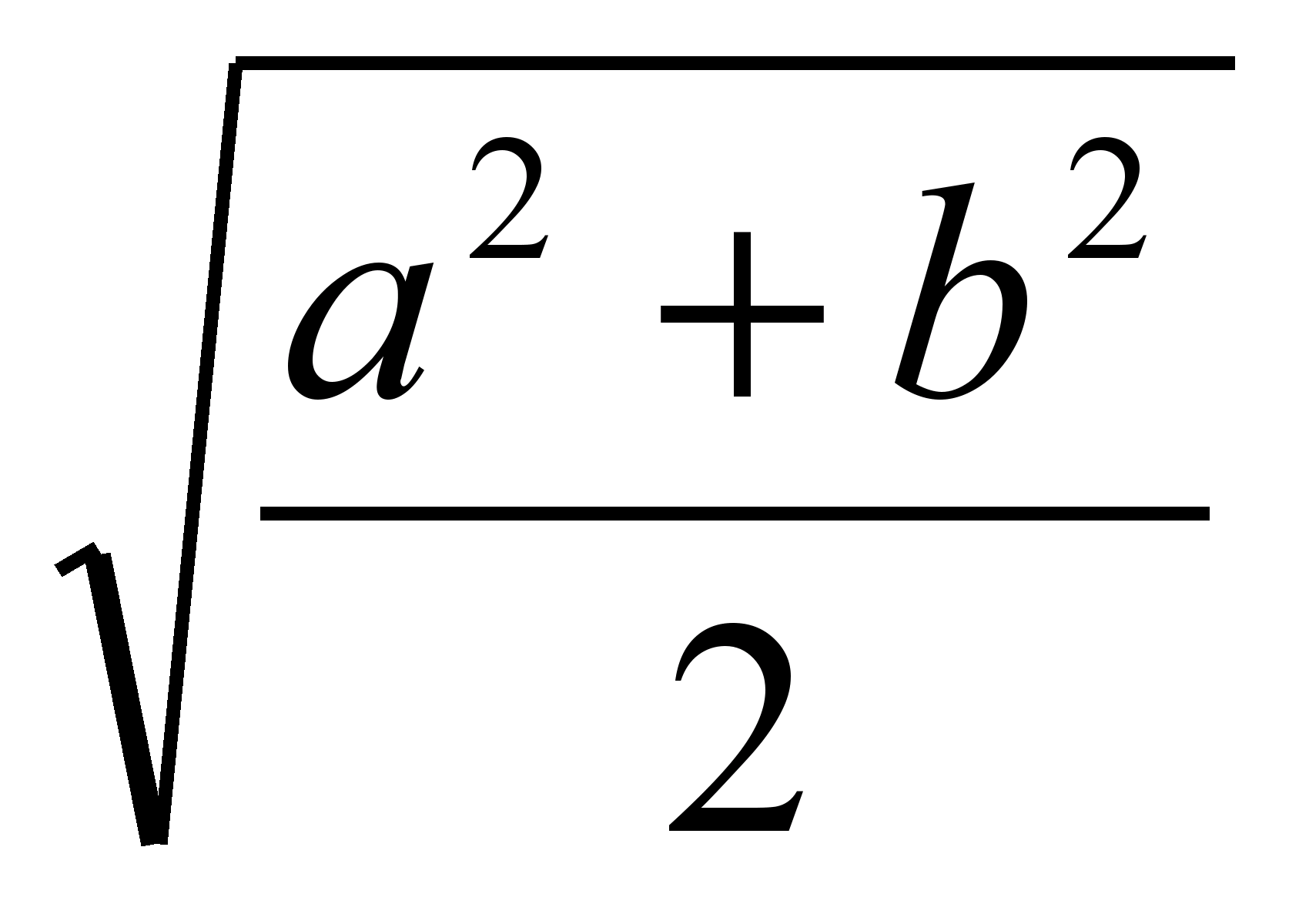 (mittlere quadratische Längen der Basen).
).
(mittlere quadratische Längen der Basen).
).
Die Liste der Lektionen entspricht jetzt den kurzen Zusammenfassungen. Bei einem gleichschenkligen Trapez sind die Grundwinkel deckungsgleich. Satz 2. Wenn die Basiswinkel in einem Trapez kongruent sind, dann ist das Trapez gleichschenklig. Gelöste Probleme Bei einem gleichschenkligen Trapez beträgt der Basiswinkel 73°. Finden Sie alle anderen Winkel des Trapezes. Bei einem gleichschenkligen Trapez beträgt der Basiswinkel das Dreifache des Innenwinkels am Ende der kürzeren Basis. Finden Sie alle Winkel des Trapezes.
Bei einem Trapez schneidet ein Liniensegment, das von der Mitte einer Seite parallel zu den Grundflächen verläuft, die andere Seite in ihrem Mittelpunkt. Finden Sie die Länge des Trapezes in der Mittellinie. Bei einem Trapez ist die große Basis 27 cm lang und 10 cm länger als die Basis.
Damit die Schüler den Zusammenhang zwischen den angegebenen Segmenten erkennen können, müssen sie aufgefordert werden, diese für ein vorgegebenes Trapez zu bauen. Ohne Schwierigkeiten können die Schüler die Mittellinie eines Trapezes und ein Segment konstruieren, das durch den Schnittpunkt der Diagonalen des Trapezes parallel zu den Basen verläuft. Wo werden das dritte und vierte Segment liegen? Die Antwort auf diese Frage sollte dazu führen, dass die Schüler die Beziehung zwischen Durchschnittswerten entdecken.
Finden Sie die Längen der trapezförmigen Grundflächen. Bei einem gleichschenkligen Trapez sind die beiden Diagonalen deckungsgleich. Aufgabe 2. Wenn zwei Diagonalen in einem Trapez kongruent sind, dann ist das Trapez gleichschenklig. Aufgabe 3. Jeder Punkt auf der Mittellinie eines Trapezes hat den gleichen Abstand von zwei parallelen Linien, die die Basen des Trapezes enthalten. Wenn ein Punkt in einer Ebene den gleichen Abstand von zwei parallelen Geraden hat, die die Grundflächen eines Trapezes enthalten, dann gehört der Punkt zu der Geraden, die die Grundflächen eines Trapezes enthält. Trapez in der Mittellinie. Problem gelöst. Bei einem Trapez wird jedes Segment einer geraden Linie, die einen Punkt auf einer kürzeren Basis mit einem Punkt auf einer größeren Basis verbindet, an der Mittellinie des Trapezes halbiert.
Das Attribut und die Eigenschaft eines beschrifteten und umschriebenen Vierecks müssen für alle den Schülern bekannten Vierecke, einschließlich des Trapezes, angegeben werden.
Eigenschaften des beschriebenen Trapezes. Ein Trapez kann genau dann um einen Kreis beschrieben werden, wenn die Summe der Grundlängen gleich der Summe der Seitenlängen ist.
Das erste liegt auf der Hand. Um die zweite Folgerung zu beweisen, muss der Winkel festgestellt werden KABELJAU direkt, was auch keine große Sache ist. Aber das Wissen um diese Konsequenz ermöglicht es uns, bei der Lösung von Problemen ein rechtwinkliges Dreieck zu verwenden.
Bei einem Trapez schneiden sich die Winkelhalbierenden der Innenwinkel an den Enden der lateralen Seite im rechten Winkel. Bei einem Trapez schneiden sich die Winkelhalbierenden der Innenwinkel an den Enden der lateralen Seite in einem Punkt, der auf der Mittellinie des Trapezes liegt. Aufgabe 4. Bei einem gleichschenkligen Trapez beträgt der Basiswinkel 60°. Beweisen Sie, dass die kürzere Basislänge gleich der Differenz zwischen der längeren Basislänge und der Länge der lateralen Seite ist.
Bei einem gleichschenkligen Trapez beträgt die Diagonale 10 cm und steht im Winkel von 60° zur Basis. Ermitteln Sie die Länge eines mittellangen Trapezes. Die Grundflächen des Trapezes sind 3 und 5 Einheiten lang, eine Diagonale verläuft senkrecht zur Seite und die andere Diagonale halbiert den Winkel. auf einer größeren Basis. Finden Sie die Höhe des Trapezes. Konstruieren Sie mit einem Lineal und einem Zirkel ein Trapez, dessen Grundflächen den beiden vorgegebenen Segmenten entsprechen, und Seiten, kongruent. zwei weitere vorgegebene Segmente.
Lassen Sie uns die Konsequenzen für spezifizieren gleichschenkliges umschriebenes Trapez :
|
|
Die Höhe eines umschriebenen gleichschenkligen Trapezes ist das geometrische Mittel der Basen des Trapezes. Diagonalen und Winkel eines TrapezesKonstruieren Sie mit einem Lineal und einem Zirkel ein Trapez, dessen Grundflächen den beiden vorgegebenen Segmenten entsprechen und dessen Seiten deckungsgleich sind. zu zwei anderen gegebenen Segmenten. Geometrie ist ein spezielles Fach der Mathematik, das sich mit Formen und Objekten und den damit verbundenen Problemen befasst. Existieren verschiedene Typen geometrische Formen. Einige wichtige 2D-Formen sind Quadrat, Rechteck, Dreieck, Polygon, Kreis, Parallelogramm, Trapez, Raute usw. Eine durch vier Seiten begrenzte Form wird Viereck genannt. |
Betrachten Sie die Grundprinzipien der Methodik zur Untersuchung der Eigenschaften eines Trapezes.
Erstens ist es die Verwendung Aufgabenansatz . Es besteht keine Notwendigkeit, neue Eigenschaften des Trapezes in den theoretischen Kurs der Geometrie einzuführen. Diese Eigenschaften werden von den Studierenden durch Problemlösung entdeckt und formuliert (besser als bei Problemsystemen). Es ist wichtig, dass der Lehrer weiß, welche Aufgaben an welchem Punkt des Lernprozesses gestellt werden sollen. Darüber hinaus kann jede Eigenschaft eine Schlüsselaufgabe im Aufgabensystem sein.
Zweitens, „spiralförmige“ Organisation zur Untersuchung der Eigenschaften eines Trapezes
. Sie können zu einzelnen Objekten mehrmals zurückkehren, dann ist es wahrscheinlich, dass sich die Studierenden daran erinnern. Beispielsweise kann die Eigenschaft von vier Punkten bewiesen werden, indem die Ähnlichkeit untersucht und dann Vektoren verwendet werden. Die gleiche Fläche von Dreiecken, die an die Seiten eines Trapezes angrenzend sind, kann anhand der Eigenschaft von Dreiecken mit bewiesen werden gleiche Höhen, auf die Seiten gezogen, die auf einer geraden Linie liegen, und die Formel 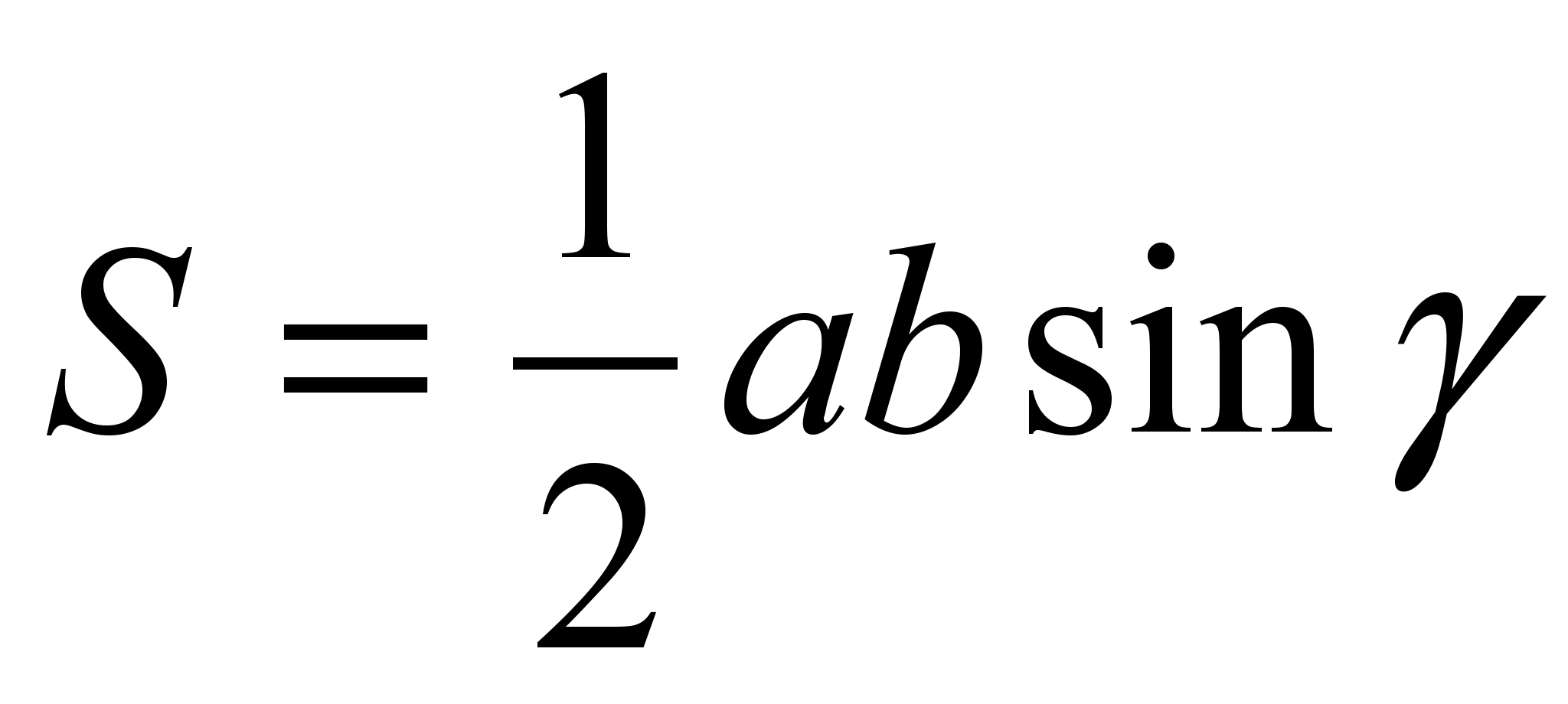 . Sie können die Eigenschaften eines rechtwinkligen Dreiecks auf dem umschriebenen Trapez, den Sinussatz auf dem eingeschriebenen Trapez usw. berechnen.
. Sie können die Eigenschaften eines rechtwinkligen Dreiecks auf dem umschriebenen Trapez, den Sinussatz auf dem eingeschriebenen Trapez usw. berechnen.
Die vorgeschlagene Einbeziehung „nicht programmbezogener“ Eigenschaften des Trapezes in den Inhalt des schulischen Geometriekurses, die Aufgabentechnik für deren Studium, die wiederholte Bezugnahme auf die Eigenschaften des Trapezes beim Studium anderer Themen werden den Schülern ein tieferes Verständnis des Trapezes ermöglichen und den Erfolg bei der Lösung von Problemen bei der Anwendung seiner Eigenschaften sicherstellen.
Deshalb werden wir einen von ihnen anrufen groß
, zweite - kleine Basis
Trapez. Höhe
Ein Trapez kann als jedes Segment einer Senkrechten bezeichnet werden, das von den Scheitelpunkten zur entsprechenden gegenüberliegenden Seite gezogen wird (für jeden Scheitelpunkt gibt es zwei gegenüberliegende Seiten), das zwischen dem aufgenommenen Scheitelpunkt und der gegenüberliegenden Seite eingeschlossen ist. Aber man kann es hervorheben besondere Art"Höhen.
Definition 8.
Die Höhe der Basis eines Trapezes ist das zwischen den Basen eingeschlossene Segment einer geraden Linie senkrecht zu den Basen.
Satz 7
. Die Mittellinie des Trapezes verläuft parallel zu den Grundflächen und entspricht der Hälfte ihrer Summe.
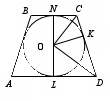
Nachweisen. Gegeben seien das Trapez ABCD und die Mittellinie KM. Zeichnen Sie eine Linie durch die Punkte B und M. Wir setzen die Seite AD durch Punkt D fort, bis sie BM schneidet. Die Dreiecke BCm und MPD haben die gleichen Seiten- und zwei Winkel (CM=MD, ∠ BCM=∠ MDP – überlappend, ∠ BMC=∠ DMP – vertikal), daher ist VM=MP oder Punkt M der Mittelpunkt von BP. KM ist die Mittellinie im Dreieck ABP. Gemäß der Eigenschaft der Mittellinie des Dreiecks verläuft KM parallel zu AP und insbesondere zu AD und ist gleich der Hälfte von AP: 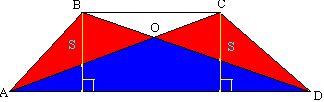 Satz 8
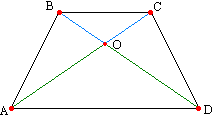
. Die Diagonalen teilen das Trapez in vier Teile, von denen zwei an den Seiten gleich sind.
Satz 8
. Die Diagonalen teilen das Trapez in vier Teile, von denen zwei an den Seiten gleich sind.
Ich möchte Sie daran erinnern, dass Figuren als gleich bezeichnet werden, wenn sie die gleiche Fläche haben. Die Dreiecke ABD und ACD sind gleich: Sie haben die gleiche Höhe (gelb dargestellt) und eine gemeinsame Basis. Diese Dreiecke haben einen gemeinsamen Teil AOD. Ihr Bereich kann wie folgt erweitert werden: 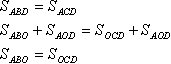
 Arten von Trapezen:
Arten von Trapezen:
Definition 9.
(Abbildung 1) Ein spitzwinkliges Trapez ist ein Trapez, bei dem die Winkel neben der größeren Basis spitz sind.
Definition 10.
(Abbildung 2) Ein stumpfes Trapez ist ein Trapez, bei dem einer der Winkel neben der größeren Basis stumpf ist.
Definition 11.
(Abbildung 4) Ein Trapez wird als Rechteck bezeichnet, bei dem eine Seite senkrecht zu den Basen steht.
Definition 12.
(Abbildung 3) Isosceles (gleichschenklig, gleichschenklig) ist ein Trapez, bei dem die Seiten gleich sind.
 Eigenschaften eines gleichschenkligen Trapezes:
Eigenschaften eines gleichschenkligen Trapezes:
Satz 10
. Die Winkel neben den Grundflächen eines gleichschenkligen Trapezes sind gleich.
Nachweisen. Beweisen wir zum Beispiel die Gleichheit der Winkel A und D mit einer größeren Basis AD eines gleichschenkligen Trapezes ABCD. Dazu zeichnen wir eine Gerade durch den Punkt C parallel zur lateralen Seite AB. Es schneidet die große Basis im Punkt M. Das Viereck ABCM ist ein Parallelogramm, weil Aufgrund seiner Konstruktion hat es zwei Paare paralleler Seiten. Daher ist das Segment CM der im Inneren des Trapezes eingeschlossenen Sekantenlinie gleich seiner lateralen Seite: CM=AB. Daraus ist klar, dass CM=CD, das Dreieck CMD gleichschenklig ist, ∠CMD=∠CDM und daher ∠A=∠D. Die Winkel neben der kleineren Basis sind ebenfalls gleich, weil sind für die gefundenen inneren einseitig und haben eine Summe von zwei Zeilen. 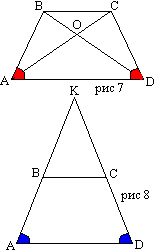 Satz 11
. Die Diagonalen eines gleichschenkligen Trapezes sind gleich.
Satz 11
. Die Diagonalen eines gleichschenkligen Trapezes sind gleich.
Nachweisen. Betrachten Sie die Dreiecke ABD und ACD. Er ist auf zwei Seiten und dem Winkel zwischen ihnen gleich (AB=CD, AD ist gemeinsam, Winkel A und D sind nach Satz 10 gleich). Daher ist AC=BD.
 Satz 13
. Die Diagonalen eines gleichschenkligen Trapezes werden durch den Schnittpunkt in entsprechend gleiche Segmente unterteilt. Betrachten Sie die Dreiecke ABD und ACD. Er ist auf zwei Seiten und dem Winkel zwischen ihnen gleich (AB=CD, AD ist gemeinsam, Winkel A und D sind nach Satz 10 gleich). Daher ist ∠ ОАD=∠ ОDA, daher sind die Winkel ОВС und OSV gleich wie die entsprechenden überlappenden Winkel ODA und ОАD. Erinnern Sie sich an den Satz: Wenn zwei Winkel in einem Dreieck gleich sind, dann ist es gleichschenklig, daher sind die Dreiecke ОВС und ОAD gleichschenklig, was bedeutet, dass OS=OB und ОА=OD usw.
Satz 13
. Die Diagonalen eines gleichschenkligen Trapezes werden durch den Schnittpunkt in entsprechend gleiche Segmente unterteilt. Betrachten Sie die Dreiecke ABD und ACD. Er ist auf zwei Seiten und dem Winkel zwischen ihnen gleich (AB=CD, AD ist gemeinsam, Winkel A und D sind nach Satz 10 gleich). Daher ist ∠ ОАD=∠ ОDA, daher sind die Winkel ОВС und OSV gleich wie die entsprechenden überlappenden Winkel ODA und ОАD. Erinnern Sie sich an den Satz: Wenn zwei Winkel in einem Dreieck gleich sind, dann ist es gleichschenklig, daher sind die Dreiecke ОВС und ОAD gleichschenklig, was bedeutet, dass OS=OB und ОА=OD usw.
Ein gleichschenkliges Trapez ist eine symmetrische Figur.
Definition 13.
Die Symmetrieachse eines gleichschenkligen Trapezes wird als Gerade bezeichnet, die durch die Mittelpunkte seiner Grundflächen verläuft.
Satz 14
. Die Symmetrieachse eines gleichschenkligen Trapezes steht senkrecht zu seinen Grundflächen. 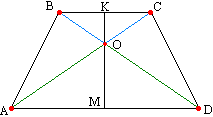 In Satz 9 haben wir bewiesen, dass die Linie, die die Mittelpunkte der Basen eines Trapezes verbindet, durch den Schnittpunkt der Diagonalen verläuft. Als nächstes (Satz 13) haben wir bewiesen, dass die Dreiecke AOD und BOC gleichschenklig sind. OM und OK sind per Definition jeweils die Mediane dieser Dreiecke. Erinnern Sie sich an die Eigenschaft eines gleichschenkligen Dreiecks: Der Mittelwert eines gleichschenkligen Dreiecks, auf die Basis abgesenkt, ist auch die Höhe des Dreiecks. Aufgrund der Rechtwinkligkeit der Basen der Teile der Geraden KM steht die Symmetrieachse senkrecht auf den Basen.
In Satz 9 haben wir bewiesen, dass die Linie, die die Mittelpunkte der Basen eines Trapezes verbindet, durch den Schnittpunkt der Diagonalen verläuft. Als nächstes (Satz 13) haben wir bewiesen, dass die Dreiecke AOD und BOC gleichschenklig sind. OM und OK sind per Definition jeweils die Mediane dieser Dreiecke. Erinnern Sie sich an die Eigenschaft eines gleichschenkligen Dreiecks: Der Mittelwert eines gleichschenkligen Dreiecks, auf die Basis abgesenkt, ist auch die Höhe des Dreiecks. Aufgrund der Rechtwinkligkeit der Basen der Teile der Geraden KM steht die Symmetrieachse senkrecht auf den Basen.
Zeichen, die ein gleichschenkliges Trapez unter allen Trapezen unterscheiden:
Satz 15
. Wenn die Winkel neben einer der Basen eines Trapezes gleich sind, dann ist das Trapez gleichschenklig.
Satz 16
. Wenn die Diagonalen eines Trapezes gleich sind, dann ist das Trapez gleichschenklig.
Satz 17
. Wenn die Seiten des Trapezes, bis zum Schnittpunkt verlängert, zusammen mit seiner großen Basis ein gleichschenkliges Dreieck bilden, dann ist das Trapez gleichschenklig.
Satz 18
. Wenn ein Trapez in einen Kreis eingeschrieben werden kann, dann ist es gleichschenklig.
Zeichen eines rechteckigen Trapezes:
Satz 19
. Jedes Viereck mit nur zwei rechten Winkeln an benachbarten Eckpunkten ist ein rechtwinkliges Trapez (es ist offensichtlich, dass die beiden Seiten parallel sind, weil einseitig gleich sind. Wenn drei rechte Winkel ein Rechteck sind)
Satz 20
. Der Radius eines in ein Trapez eingeschriebenen Kreises entspricht der halben Höhe der Grundfläche. 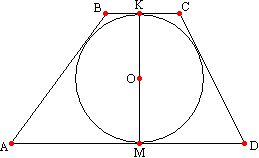 Der Beweis dieses Theorems besteht darin, zu erklären, dass die zu den Basen gezeichneten Radien auf der Höhe des Trapezes liegen. Vom Punkt O – dem Mittelpunkt des in dieses Trapez eingeschriebenen Kreises ABCD – zeichnen wir die Radien zu den Kontaktpunkten mit seinen Basen des Trapezes. Wie Sie wissen, steht der zum Kontaktpunkt gezeichnete Radius senkrecht zur Tangente, also OK ^ BC und OM ^ AD. Erinnern Sie sich an den Satz: Wenn eine Gerade senkrecht zu einer der parallelen Geraden steht, dann steht sie auch senkrecht zur zweiten. Daher steht die Gerade OK auch senkrecht auf AD. Somit verlaufen zwei Geraden senkrecht zur Geraden AD durch den Punkt O, was nicht möglich ist, daher fallen diese Geraden zusammen und bilden die gemeinsame Senkrechte KM, die gleich der Summe zweier Radien und dem Durchmesser des eingeschriebenen Kreises ist, also r=KM/2 oder r=h/2.
Der Beweis dieses Theorems besteht darin, zu erklären, dass die zu den Basen gezeichneten Radien auf der Höhe des Trapezes liegen. Vom Punkt O – dem Mittelpunkt des in dieses Trapez eingeschriebenen Kreises ABCD – zeichnen wir die Radien zu den Kontaktpunkten mit seinen Basen des Trapezes. Wie Sie wissen, steht der zum Kontaktpunkt gezeichnete Radius senkrecht zur Tangente, also OK ^ BC und OM ^ AD. Erinnern Sie sich an den Satz: Wenn eine Gerade senkrecht zu einer der parallelen Geraden steht, dann steht sie auch senkrecht zur zweiten. Daher steht die Gerade OK auch senkrecht auf AD. Somit verlaufen zwei Geraden senkrecht zur Geraden AD durch den Punkt O, was nicht möglich ist, daher fallen diese Geraden zusammen und bilden die gemeinsame Senkrechte KM, die gleich der Summe zweier Radien und dem Durchmesser des eingeschriebenen Kreises ist, also r=KM/2 oder r=h/2.
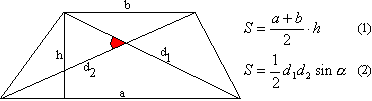
Satz 21
. Die Fläche eines Trapezes ist gleich dem Produkt aus der halben Summe der Grundflächen und der Höhe der Grundflächen. 
Nachweisen: Sei ABCD ein gegebenes Trapez und AB und CD seien seine Basen. Sei auch AH die Höhe, die vom Punkt A zur Linie CD fällt. Dann ist S ABCD = S ACD + S ABC .
Aber S ACD = 1/2AH CD und S ABC = 1/2AH AB.
Daher ist S ABCD = 1/2AH (AB + CD).
Q.E.D.
 Die zweite Formel hat sich vom Viereck entfernt.
Die zweite Formel hat sich vom Viereck entfernt.
Es könnte nützlich sein zu lesen:
- Was bedeutet die Rune Kenaz bei der Wahrsagerei für Arbeit und Geschäft?;
- Wahrsagerei auf Wachs über die Bedeutung von Schneemannfiguren;
- Wahrsagerei auf Wachs über die Bedeutung der Figuren;
- Mit Kronleuchtern verbundene Schilder;
- Zeichen - die rechte Augenbraue juckt;
- Was verspricht der juckende Nasenrücken?;
- Zahlen – das größte Zeichen des Allmächtigen;
- Jeden Tag Suren und Verse aus dem Koran lesen;
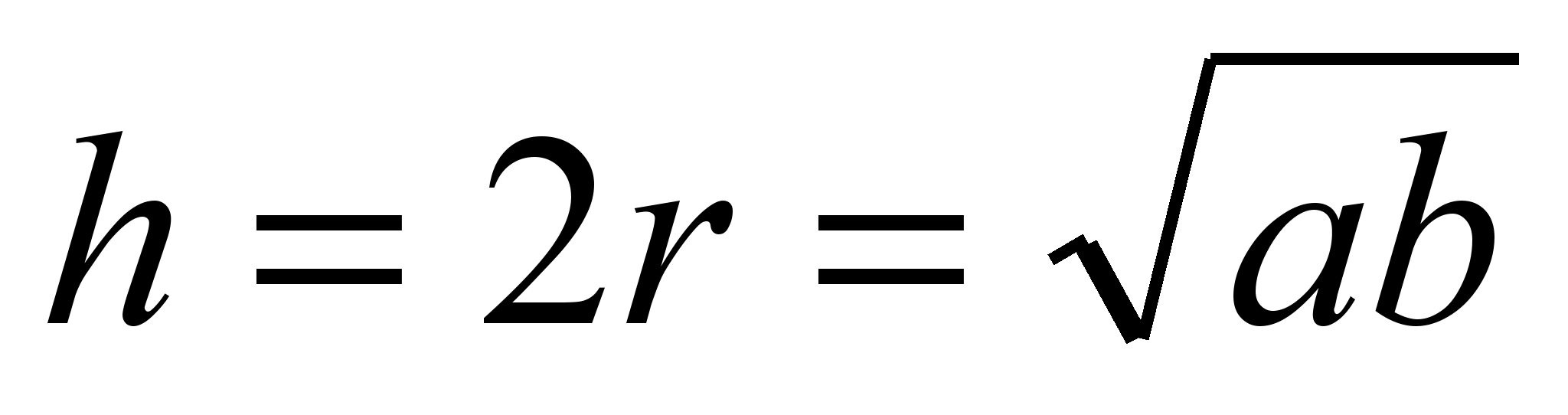 .
.