So finden Sie die Seite eines Zylinders. So finden Sie die Fläche eines Zylinders
Ein Zylinder ist eine Figur, die aus einer Zylinderfläche und zwei parallel angeordneten Kreisen besteht. Die Berechnung der Fläche eines Zylinders ist ein Problem im geometrischen Zweig der Mathematik, das ganz einfach gelöst wird. Es gibt mehrere Lösungsansätze, die im Ergebnis immer auf eine Formel hinauslaufen.
So finden Sie die Fläche eines Zylinders - Berechnungsregeln
- Um die Fläche des Zylinders herauszufinden, müssen Sie zwei Grundflächen mit der Fläche der Seitenfläche hinzufügen: S \u003d S Seite + 2 S Haupt. In einer detaillierteren Version sieht diese Formel so aus: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Die Seitenfläche eines gegebenen geometrischen Körpers kann berechnet werden, wenn seine Höhe und der Radius des der Grundfläche zugrunde liegenden Kreises bekannt sind. IN dieser Fall Es ist möglich, den Radius aus dem Umfang eines Kreises auszudrücken, wenn er angegeben ist. Die Höhe kann ermittelt werden, wenn der Wert der Erzeugenden in der Bedingung angegeben ist. In diesem Fall ist die Erzeugende gleich der Höhe. Die Formel für die Mantelfläche eines gegebenen Körpers sieht so aus: S= 2 π rh.
- Die Fläche der Basis wird nach der Formel zum Ermitteln der Fläche eines Kreises berechnet: S osn= π r 2 . Bei einigen Aufgaben ist der Radius möglicherweise nicht angegeben, aber der Umfang ist angegeben. Mit dieser Formel lässt sich der Radius ganz einfach ausdrücken. С=2π r, r= С/2π. Es muss auch daran erinnert werden, dass der Radius der halbe Durchmesser ist.
- Bei all diesen Berechnungen wird die Zahl π normalerweise nicht in 3,14159 übersetzt ... Sie müssen sie nur neben hinzufügen numerischer Wert, die als Ergebnis der Berechnungen erhalten wurde.
- Außerdem muss nur die gefundene Fläche der Basis mit 2 multipliziert und zur resultierenden Zahl die berechnete Fläche der Seitenfläche der Figur addiert werden.
- Wenn das Problem anzeigt, dass der Zylinder einen axialen Abschnitt hat und dies ein Rechteck ist, dann wird die Lösung etwas anders sein. In diesem Fall entspricht die Breite des Rechtecks dem Durchmesser des Kreises, der an der Basis des Körpers liegt. Die Länge der Figur entspricht der Erzeugenden oder der Höhe des Zylinders. Es ist notwendig, die gewünschten Werte zu berechnen und in eine bereits bekannte Formel einzusetzen. In diesem Fall muss die Breite des Rechtecks durch zwei geteilt werden, um die Fläche der Basis zu finden. Um die Seitenfläche zu finden, wird die Länge mit zwei Radien und mit der Zahl π multipliziert.
- Sie können die Fläche eines bestimmten geometrischen Körpers durch sein Volumen berechnen. Dazu müssen Sie den fehlenden Wert aus der Formel V=π r 2 h ableiten.
- Es ist nicht schwierig, die Fläche eines Zylinders zu berechnen. Sie müssen nur die Formeln kennen und daraus die für die Berechnungen notwendigen Größen ableiten können.
Ein Zylinder hat drei Oberflächen: oben, unten und Seitenfläche.
Die Ober- und Unterseite des Zylinders sind Kreise und leicht zu erkennen.
Es ist bekannt, dass die Fläche eines Kreises gleich πr2 ist. Daher sieht die Formel für die Fläche zweier Kreise wie folgt aus: πr2 + πr2 = 2πr2.
Mantelfläche des Zylinders
Die dritte Seitenfläche des Zylinders ist die gekrümmte Wand des Zylinders. Um diese Oberfläche besser darzustellen, versuchen wir, sie zu transformieren, um eine erkennbare Form zu erhalten. Stellen Sie sich vor, dass ein Zylinder eine gewöhnliche Blechdose ist, die keinen oberen und unteren Deckel hat. Lassen Sie uns einen vertikalen Schnitt an der Seitenwand von oben nach unten machen und versuchen, die resultierende Figur zu maximieren.
Nach der vollständigen Offenlegung des resultierenden Glases sehen wir eine bekannte Figur, dies ist ein Rechteck. Die Fläche eines Rechtecks lässt sich leicht berechnen. Doch kehren wir vorher noch kurz zum Originalzylinder zurück. Der Scheitelpunkt des ursprünglichen Zylinders ist ein Kreis, und wir wissen, dass der Umfang eines Kreises nach folgender Formel berechnet wird: L = 2πr. In der Abbildung ist er rot markiert.
Wenn die Seitenwand des Zylinders vollständig erweitert ist, sehen wir, dass der Umfang zur Länge des resultierenden Rechtecks wird. Die Seiten dieses Rechtecks sind der Umfang und die Höhe des Zylinders. Die Fläche eines Rechtecks ist gleich dem Produkt seiner Seiten - S = Länge x Breite = L x h = 2πr x h = 2πrh. Als Ergebnis haben wir eine Formel zur Berechnung der Mantelfläche eines Zylinders erhalten.
Die Formel für die Fläche der Mantelfläche eines Zylinders
Seite = 2prh
Vollständige Oberfläche eines Zylinders
Wenn wir schließlich die Fläche aller drei Flächen addieren, erhalten wir die Formel für die Gesamtfläche...
Zylinderoberfläche. Die Oberfläche des Zylinders ist gleich der Fläche der Oberseite des Zylinders + der Fläche der Basis des Zylinders + der Fläche der Seitenfläche des Zylinders oder S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Manchmal wird dieser Ausdruck durch die identische Formel 2πr geschrieben.
Die Formel für die Gesamtfläche eines Zylinders
S = 2πr2 + 2πrh = 2πr
r ist der Radius des Zylinders, h ist die Höhe des Zylinders
Beispiele für die Berechnung der Oberfläche eines Zylinders
Um die obigen Formeln zu verstehen, versuchen wir anhand von Beispielen die Oberfläche eines Zylinders zu berechnen.
1. Der Radius der Basis des Zylinders beträgt 2, die Höhe 3. Bestimmen Sie die Fläche der Seitenfläche des Zylinders
Die Gesamtfläche wird nach folgender Formel berechnet: SSeite. = 2prh
Seite = 2 * 3,14 * 2 * 3
Seite = 6,28 * 6
Seite = 37,68
Die Mantelfläche des Zylinders beträgt 37,68.
2. Wie findet man die Oberfläche eines Zylinders, wenn die Höhe 4 und der Radius 6 ist?
Die Gesamtoberfläche wird nach folgender Formel berechnet: S = 2πr2 + 2πrh
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
Die Oberfläche des Zylinders beträgt 376,8.
3 Die Seitenfläche eines geraden Kreiszylinders ist 24π und der Basisdurchmesser ist 3. Finde die Höhe des Zylinders.
Aus der Formel zur Berechnung der Fläche der Mantelfläche des Zylinders Sbok. = 2πrh ergibt sich für die Höhe:
H = SSeite/2πr
Der Radiuswert ergibt sich aus der Formel: d = 2r
Die Höhe des Zylinders beträgt 8.
(Noch keine Bewertungen)
- Der Zweck der Lektion: die Rolle von Energieparametern herauszufinden, wobei der Hauptparameter die Dichte des Strahlungsflusses zu den Empfängern der ausgestrahlten elektromagnetischen Wellen ist. Unterrichtsfortschritt Überprüfung der Hausaufgaben durch Testen 1. 1887 wurden sie experimentell ...
- Erst die jüngere Geschichte hat die alte Handelsstadt Zittau ins Abseits gerückt. In den umliegenden Dörfern des Hausgebirges wurde das Zittauer Leinen gewebt. Ende des 17. Jahrhunderts war sie nach... Der Zweck des Unterrichts: die Fähigkeit zu bilden, die Bewegung eines Punktes mit variabler Beschleunigung zu beschreiben; Zentripetalbeschleunigung, Linear- und Winkelgeschwindigkeit bei gleichförmiger Bewegung eines Punktes entlang eines Kreises bestimmen. Unterrichtsfortschritt Kontrolle der Hausaufgaben durch selbstständiges ...
- Bei der Herstellung von Produkten aus Holzwerkstoffen mit einer Stichsäge bleiben Unregelmäßigkeiten an ihren Kanten zurück, die geebnet und gereinigt werden müssen. Solche technologischen Operationen werden mit Feilen und Schleifhäuten durchgeführt. Die Feile ist eine mehrschneidige...
- Der Zweck der Lektion: eine Gleichung zu erhalten, die den Schwingungsvorgang an jedem Punkt im Raum während der Ausbreitung einer Welle beschreibt; wie sich Wellen in einem Medium ausbreiten. Während des Unterrichts. Überprüfung der Hausaufgaben durch Einzelbefragung 1. Laut Plakat ...
- Der Zweck der Lektion: Entwicklung von Fähigkeiten zur Lösung von Problemen unter Verwendung der Konzepte von Spannung, Potenzial und der Arbeit eines elektrischen Felds zum Bewegen einer Ladung; weiterhin die Fähigkeit zu denken, zu vergleichen, Schlussfolgerungen zu ziehen, Notizen in Notizbüchern zu machen. Während des Unterrichts ...
- Der Zweck des Unterrichts: Kontrolle über das Wissen und die Fähigkeiten der Schüler, die beim Studium des Themas erworben wurden. Während des Unterrichts Zeit organisieren. Durchführung von Kontrollarbeiten. Option - 1 (Level - 1) 1 Beim Springen in ...
Betrachten Sie einen Rotationszylinder mit Radius R und Höhe h (Abb. 383). In die Basis dieses Zylinders werden wir ein regelmäßiges Polygon (in Abb. 383 - ein Sechseck) einschreiben und mit seiner Hilfe ein regelmäßiges Prisma konstruieren, das in den Zylinder eingeschrieben ist. Ebenso lassen sich um den Zylinder herum regelmäßige Prismen mit beliebig vielen Seitenflächen beschreiben.
Definitionsgemäß ist die Fläche der Mantelfläche des Zylinders die Grenze, zu der die Flächen der Mantelflächen der um ihn herum eingeschriebenen und beschriebenen regelmäßigen Prismen tendieren, wenn sich die Anzahl ihrer Seitenflächen verdoppelt (bzw sogar erhöht) auf unbestimmte Zeit.
Dass eine solche Grenze existiert, werden wir nun beweisen. Wenn wir ein einbeschriebenes regelmäßiges Prisma nehmen, das auf einem regelmäßigen -Eck wie auf der Basis aufgebaut ist, dann haben wir für seine Seitenfläche den Ausdruck , wobei der Umfang eines regelmäßigen -Ecks ist, das in den Kreis der Basis des Zylinders eingeschrieben ist. Bei . Genau die gleiche Rechnung für das beschriebene Prisma ergibt das gleiche Ergebnis. Die Fläche der Mantelfläche eines Rotationszylinders wird also durch die Formel ausgedrückt
![]()
Die Seitenfläche des Zylinders ist gleich dem Produkt aus der Länge der Erzeugenden und dem Umfang (d. h. dem Umfang) der Basis.
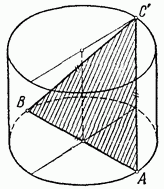
Problem 1. Das Segment, das die diametral gegenüberliegenden Punkte A und B der oberen und unteren Basis des Zylinders verbindet (Abb. 384), ist 10 cm lang und in einem Winkel von 60 ° zur Ebene der Basis geneigt. Finden Sie die Fläche der Mantelfläche des Zylinders.
Lösung. Lassen Sie uns das Ereignis durch das Segment A durch eine Ebene zeichnen, die senkrecht zur Basis des Zylinders steht. Aus dem Dreieck haben wir
woher wir für die Seitenfläche des Zylinders finden
Finden Sie den Neigungswinkel zur gleichen Ebene der Diagonalen des Parallelepipeds.
2. In einem geraden Parallelepiped ist der spitze Winkel der Basis gleich a, und eine der Seiten der Basis ist gleich a. Der durch diese Seite und die gegenüberliegende Kante der oberen Basis gezogene Schnitt hat die Fläche Q, und seine Ebene ist in einem Winkel zur Ebene der Basis geneigt. Finden Sie das Volumen und die Gesamtfläche des Parallelepipeds.
3. Die Basis eines geneigten dreieckigen Prismas ist gleichschenklig rechtwinkliges Dreieck, und die Projektion einer der Seitenkanten auf die Ebene der Basis fällt mit dem Median m eines der Schenkel des Dreiecks zusammen. Finden Sie den Neigungswinkel der Seitenkanten zur Ebene der Basis, wenn das Volumen des Prismas V ist.
4. In einem regulären sechseckigen Prisma werden zwei Schnitte durch die Seite der Basis gezogen: 1) enthält die gegenüberliegende Seite der oberen Basis, 2) enthält die Mitte der oberen Basis. In welcher Höhe des Prismas hat der Winkel zwischen den Schnittebenen den größten Wert und wie groß ist er in diesem Fall?
Es könnte hilfreich sein zu lesen:
- Behandlung im Ausland. Keine Angst. Behandlung im Ausland - die Hauptrichtungen des Medizintourismus Behandlung im Ausland, wo es besser ist;
- Ich habe eine Frage: wie man Stress loswird;
- Die wichtigsten Tragödien im Leben von Romina Power Albano Carrisi Kinder, was sie tun;
- Was tun, wenn das Kind im Kindergarten keine Freunde sein will?;
- Koriander - nützliche Eigenschaften und Anwendung Ätherisches Korianderöl in der Kosmetik;
- Klassische Vinaigrette mit Sauerkraut - Schritt für Schritt Rezept mit Foto;
- In einem gesunden Körper ein gesunder Geist?;
- Das Verfahren zur Entlassung eines Rentners: Bestehende Gründe und Einschränkungen und wie können Sie Ihre Rechte schützen?;