Proprietățile de bază ale integralei duble. Definirea problemei integrale duble Proprietăți de bază ale integralei duble Concepte și definiții de bază ale integralei duble

Proprietățile de bază ale integralei duble

Proprietățile unei integrale duble (și derivarea lor) sunt similare cu proprietățile corespunzătoare ale unei singure integrale definite.

1°. Aditivitate. Dacă funcţia f(X, y) este integrabil în domeniu D iar dacă zona D folosind o curbă G zona zero este împărțită în două regiuni conectate care nu au puncte interioare comune D 1 și D 2, apoi funcția f(X, y) este integrabil în fiecare dintre domenii D 1 și D 2, și

2°. Proprietate liniară. Dacă funcţiile f(X, y) Și g(X, y) sunt integrabile în domenii D, A α Și β - orice numere reale, apoi funcția [ α · f(X, y) + β · g(X, y)] este de asemenea integrabil în domeniu D, și

3°. Dacă funcţiile f(X, y) Și g(X, y) sunt integrabile în domenii D, atunci produsul acestor funcții este integrabil în D.

4°. Dacă funcţiile f(X, y) Și g(X, y) ambele sunt integrabile în domeniul Dși peste tot în această zonă f(X, y) ≤ g(X, y), Acea

5°. Dacă funcţia f(X, y) este integrabil în domeniu D, apoi funcția | f(X, y)| integrabil în zone D, și

(Desigur, din integrabilitate | f(X, y)| V D integrabilitatea nu urmează f(X, y) V D.)

6°. Teorema valorii medii. Dacă ambele funcţii f(X, y) Și g(X, y) sunt integrabile în domenii D, funcție g(X, y) este nenegativ (nepozitiv) peste tot în această regiune, MȘi m- limitele superioare și inferioare exacte ale funcției f(X, y) în zonă D, apoi există un număr μ , satisfacerea inegalitatii m ≤ μ ≤ Mși astfel încât formula să fie valabilă

Problema care duce la conceptul unei integrale duble Definirea unei integrale duble Proprietăți de bază ale unei integrale duble Aria unei regiuni plane Reducerea unei integrale duble la o integrală repetată Modificarea variabilelor într-o integrală dublă Element de zonă în coordonate curbilinii Jacobiene și sensul său geometric Formula pentru schimbarea variabilelor într-o integrală dublă Integrală dublă în coordonate polare

O problemă care duce la conceptul de integrală dublă. Definiţia double integral. Ajungem la conceptul de integrală dublă rezolvând problema specifică calculării volumului unui corp cilindric. Un corp cilindric este un corp delimitat de planul xOy, o anumită suprafață și o suprafață cilindrică, ale căror generatrice sunt paralele cu axa (vezi Fig. 1). Regiunea D de modificare a variabilelor x și y se numește baza corpului cilindric. La determinarea volumului unui corp, vom pleca de la două principii: !) dacă împărțim corpul în părți, atunci volumul acestuia este egal cu suma volumelor tuturor părților (proprietatea aditivității); 2) volumul unui cilindru drept delimitat de planul z = const, paralel cu planul xOy, este egal cu aria bazei înmulțită cu înălțimea. În cele ce urmează, vom presupune că regiunea D este conectată (formată dintr-o singură bucată), pătrată (adică, având o zonă) și mărginită (adică, situată în interiorul unui anumit cerc centrat la origine). Fie o funcție continuă a punctului P(x, y) în regiunea peste tot în regiunea Z>, adică faptul că suprafața cilindrică luată în considerare se află în întregime deasupra planului xOy. Să notăm volumul unui corp cilindric cu V. Împărțim regiunea D - baza corpului cilindric - într-un anumit număr n de regiuni cadrabile neintersectate de formă arbitrară; le vom numi regiuni parțiale. După ce au numerotat zonele parțiale într-o anumită ordine, zonele - prin urmare. Să numim diametrul unei regiuni parțiale Dk mărimea Problemă care duce la conceptul de integrală dublă Definiția unei integrale duble Proprietăți de bază ale unei integrale duble Aria unei regiuni plane Reducerea unei integrale duble la o integrală repetată Modificarea de variabile într-o integrală dublă Element de zonă în coordonate curbilinii Jacobian și semnificația sa geometrică Formula de modificare a variabilelor într-o integrală dublă Integrală dublă în coordonate polare unde simbolul p(P; Q) înseamnă distanța dintre punctele P și Q. Să notăm cu d cel mai mare dintre diametrele regiunilor parțiale Dk (k = 1,2,..., n). Să desenăm prin limita fiecărei regiuni parțiale o suprafață cilindrică cu generatoare paralele cu axa Oz. Ca rezultat, corpul cilindric va fi împărțit în n corpuri cilindrice parțiale. Să înlocuim acest corp parțial cu un cilindru drept cu aceeași bază și înălțime egală cu aplicarea unui punct al suprafeței înlocuite (Fig. 2). Volumul unui astfel de cilindru este egal cu punctul în care punctul este aria regiunii Dk. După efectuarea construcțiilor descrise pentru fiecare corp cilindric parțial, obținem un corp în n trepte, al cărui volum (o) Este intuitiv clar că Vn exprimă mai precis volumul dorit V, cu atât dimensiunea regiunilor parțiale este mai mică. Dk. Considerăm că volumul V al unui corp cilindric este egal cu limita la care volumul (1) al unui corp în n trepte tinde ca n-mii, iar diametrul cel mai mare d al regiunilor parțiale Dk tinde spre zero. Desigur, limita nu ar trebui să depindă de tipul de partiție a regiunii D în regiuni parțiale Dk și de alegerea punctelor Pk în regiunile parțiale. Fie /(x, y) o funcție arbitrară definită în domeniul D. Suma n (1) se numește sumă integrală pentru funcția f(x)y) peste domeniul D, corespunzătoare unei partiții date a acestui domeniu în n domenii parțiale și o alegere dată de puncte Ж ®*,!/*) pe domenii parțiale Dk. Definiție. Dacă pentru d -* 0 există o limită a sumelor integrale n care nu depinde nici de metoda de împărțire a domeniului D în domenii parțiale, nici de alegerea punctelor Pk din domeniile parțiale, atunci se numește integrală dublă a funcția f(P) (sau f(x, y )) peste domeniul D și se notează cu simbolul SAU Deci, (2) Funcția însăși f(x, y) se numește integrabilă în domeniul D (f( P) este integrandul, f(P) dS este integrandul, dS este diferenţialul (sau elementul) ariei, regiunea D - regiunea de integrare; punctul P(®, y) - fineţea variabilă a integrării). ,.. Revenind la corpul cilindric, conchidem: volumul unui corp cilindric delimitat de planul xOy, suprafata, si o suprafata cilindrica cu generatrice paralela cu axa Oz, este egal cu integrala dubla a functiei /( x, y) peste regiunea D, care este baza corpului cilindric. / SAU Aici dx dy este elementul de zonă în coordonate carteziene. Acesta este sensul geometric al integralei duble a unei funcții nenegative. Dacă atunci volumul Dacă în regiunea D a funcției f(P) ia atât valori pozitive, cât și negative, atunci integrala reprezintă suma algebrică a volumelor acelor părți ale corpului care sunt situate deasupra planului xOy (luată cu un semn „+”) și acele părți ale corpului care sunt situate sub planul xOy (luate cu semnul „-”). O mare varietate de probleme, nu doar problema volumului unui corp cilindric, conduc la compilarea de sume de forma (1) pentru o funcție a două variabile independente și trecerea ulterioară la limită. Să formulăm condiții suficiente pentru integrabilitate. Teorema 1. Orice funcție y) continuă într-un domeniu închis mărginit D este integrabilă în acest domeniu. Cerința pentru continuitatea integrandului se dovedește adesea a fi prea restrictivă. Pentru aplicații este importantă următoarea teoremă, care garantează existența unei integrale duble pentru o anumită clasă de funcții discontinue. Vom spune că un anumit set de puncte din plan are zonă zero dacă poate fi închis într-o figură poligonală cu o zonă arbitrar mică. Teorema 2. Dacă o funcție /(x, y) este mărginită într-un domeniu închis și mărginit D și este continuă peste tot în D, cu excepția unei mulțimi de puncte de zonă zero, atunci această funcție este integrabilă în domeniul D. §2. Proprietățile de bază ale integralei duble Integralele duble au un număr de proprietăți similare cu proprietățile integralei definite pentru funcțiile unei variabile independente. 2.1. Proprietate liniară Dacă funcțiile) sunt integrabile în domeniul D și a și p sunt numere reale, atunci funcția af) este de asemenea integrabilă în domeniul D și o) 2.2. Integrarea inegalităților Dacă funcțiile) sunt integrabile în domeniul D și peste tot în acest domeniu, atunci (2), adică inegalitățile pot fi integrate. În special, integrând inegalitățile evidente, obținem Aria unei regiuni plate Aria unei regiuni plate D este egală cu integrala dublă peste această regiune a unei funcții identic egală cu unitatea. Într-adevăr, suma integrală pentru funcția /(P) = 1 din domeniul D are forma și, pentru orice partiție a domeniului D în domenii parțiale Dt, este egală cu aria sa S. Dar atunci limita acestei sume, adică, integrala dublă, este egală cu aria S aria D: sau, ceea ce este același, (3) 2.4. Estimarea integralei Fie funcția /(P) continuă într-o regiune închisă mărginită D, fie M și mn cele mai mari și mai mici valori ale /(P) în regiunea D și 5 aria acesteia. Apoi (4) 2.5. Aditivitate: Dacă funcția /(P) este integrabilă în domeniul D și domeniul Z) este împărțit în două domenii D\ și Di fără puncte interne comune, atunci /(P) este integrabil pe fiecare dintre domeniile D\ și Di , și (5) 2.6. Teorema valorii medii Teorema 3 (valoarea medie). Dacă funcția /(P) este continuă într-un domeniu închis și mărginit D, atunci există cel puțin un punct Pc al domeniului D astfel încât formula și unde S este aria domeniului D este valabilă. Într-adevăr, deoarece /(P) este continuă într-un domeniu închis și mărginit D, apoi ia în D cea mai mare valoare a sa M și cea mai mică valoare a sa m. Prin proprietatea 4 asupra estimarii integralei avem Astfel, numărul este cuprins între cea mai mare și cea mai mică valorile funcției /(P) în domeniul D. Datorită continuității funcției /( P) în domeniul D ia la un moment dat Pc G D o valoare egală cu acest număr, de unde S Valoarea f( Pc), determinată prin formula (7), se numește valoarea medie a funcției f(P) în domeniul D. Semnificația geometrică a valorii teoremei valorii medii Dacă în regiunea D funcția /(P) ^ O, atunci formula (6) înseamnă că există un cilindru drept cu o bază D (a cărui zonă este 5) și o înălțime H = /(Pc), al cărui volum este egal cu volumul corpului cilindric (Fig. . 3). § 3. Reducerea unei integrale duble la o integrală iterată Una dintre modalitățile eficiente de a calcula o integrală dublă este reducerea acesteia la o integrală iterată. 3.1. Cazul unui dreptunghi Fie aria D un dreptunghi închis P cu laturile paralele cu axele de coordonate. Fie funcția f(x, y) continuă în dreptunghiul P. Integrala dublă poate fi interpretată ca volumul (algebric) al unui corp cilindric cu baza P, mărginit de o suprafață.Se consideră corpul cilindric corespunzător. Să desenăm un plan perpendicular pe axa Oy (Fig. 4). Acest plan va diseca corpul cilindric de-a lungul unui trapez curbiliniu delimitat de sus de o linie plată z, descrisă de ecuațiile Aria trapezului ABC\A\ este exprimată prin integrala în care integrarea se realizează peste x și yo - al doilea argument al integrandului - este considerat constant (c ^ Uo ^ d ). Valoarea integralei (1) depinde de alegerea valorii уо. Să punem (2) Expresia (2) oferă aria secțiunii transversale a unui corp cilindric a în funcție de y. Prin urmare, volumul unui corp cilindric poate fi calculat folosind formula Pe de altă parte, acest volum este exprimat prin integrala dublă a funcției /(x, y) peste dreptunghiul P. Aceasta înseamnă că înlocuirea S(y) cu expresia acesteia (2), obținem Problemă care duce la conceptul de integrală dublă Definiția unei integrale duble Proprietăți de bază ale unei integrale duble Aria unei regiuni plane Reducerea unei integrale duble la o integrală repetată Înlocuirea variabilelor într-o integrală dublă Element de zonă în coordonate curbilinii Jacobian și semnificația sa geometrică Formula de înlocuire a variabilelor într-o integrală dublă Integrală dublă în coordonate polare Ultima relație se scrie de obicei după cum urmează. Volumul unui corp cilindric poate fi găsit și din ariile secțiunii transversale ale plane x = x0. Aceasta conduce la formula (4) Fiecare dintre expresiile din partea dreaptă a formulelor (3) și (4) conține două operații succesive de integrare obișnuită a funcției /(x, y). Ele sunt numite integrale repetate ale funcției /(x, y) pe domeniul P. Dacă f(x, y) este continuă într-un dreptunghi închis P, atunci trecerea la integrale repetate este întotdeauna posibilă și (5) adică, valorile integralelor repetate ale unei funcții continue /(x, y) nu depind de ordinea integrării. Exemplul 1. Aflați integrala dublă a unei funcții pe un domeniu Avem (vezi Fig. 5): 3.2. Cazul unui domeniu arbitrar Să presupunem acum că domeniul de integrare este un domeniu închis pătrat limitat arbitrar D pe planul xOy, îndeplinind următoarea condiție: orice dreaptă paralelă cu axa Oy intersectează limita domeniului D la nr. mai mult de două puncte sau de-a lungul unui întreg segment (Fig. . 6 a). Să închidem zona D în interiorul dreptunghiului, așa cum se arată în Fig. 66. Segmentul [a, 6] este o proiecție ortogonală a regiunii D pe axa Oxy, iar segmentul [c, dj este o proiecție ortogonală a regiunii D pe axa Oy. Punctele A și C împart limita zonei D în două curbe ABC și AEC. Fiecare dintre aceste curbe se intersectează cu o linie dreaptă arbitrară paralelă cu axa Oy în cel mult un punct. Prin urmare, ecuațiile lor pot fi scrise într-o formă rezolvată în raport cu y: Fie f(x, y) o funcție continuă în regiunea D. Să disecăm corpul cilindric luat în considerare printr-un plan. În secțiune obținem un trapez curbiliniu PQMN (Fig. 7), a cărui aria este exprimată prin integrala ordinară a funcției /(x, y), considerată ca funcție a unei variabile y. În acest caz, variabila y se schimbă de la ordonata punctului P la ordonata punctului Q\ punctul P este „intrarea” dreptei x = const (în plan) în regiune - punctul „ieșirii” acesteia. din această regiune. Deoarece ecuația curbei ABC este, iar curba este, aceste ordonate pentru x luate sunt, respectiv, egale. În consecință, integrala ne oferă o expresie pentru aria unei secțiuni plane a unui corp cilindric în funcție de poziția planului de tăiere x = const. Volumul întregului corp va fi egal cu integrala acestei expresii peste x în intervalul de schimbare. Astfel, în special, pentru aria S a regiunii D obținem: Să presupunem acum că fiecare dreaptă intersectează limita regiunii D în cel mult două puncte P și Q, ale căror abscise sunt, respectiv, egale ( sau de-a lungul întregului segment) (Fig. 8). Efectuând un raționament similar, ajungem la o formulă care reduce și calculul integralei duble la unul repetat. Exemplul 2. Calculaţi integrala dublă a unei funcţii pe aria D. mărginită de drepte ^ Prima metodă. Să descriem domeniul de integrare D. Linia dreaptă y = x și parabola y = x2 se intersectează în puncte). Aceasta înseamnă că x variază în 8 limite de la 0. Orice dreaptă x = const) intersectează limita regiunii în cel mult două puncte. Prin urmare, se aplică formula (8): a doua metodă (Fig. 10). Folosind formula (10). obținem același rezultat: Exemplul 3. Calculați volumul unui corp delimitat de o suprafață intersectată cu planul xOy de-a lungul liniei unei elipse cu semi-axe datorită simetriei acestui corp față de planurile de coordonate xOz și y Ox obţinem: Notă. Dacă regiunea D este astfel încât unele linii drepte (ostratecale sau orizontale) să-și intersecteze granița în mai mult de două puncte, atunci pentru a calcula integrala dublă peste regiunea D, ar trebui să o împărțim în mod corespunzător în părți, repetați fiecare dintre integrale în părți. și adăugați rezultatele obținute. Exemplul 4. Calculați integrala dublă peste aria D cuprinsă între două pătrate cu centre și la origine și laturile paralele cu axele de coordonate, dacă latura pătratului interior este 2 și cea exterioră este 4. Este continuă ca în un pătrat mare Q, a cărui latură este 4 , iar într-un pătrat mic R. a cărui latură este egală cu 2 (Fig. 12). Conform teoremei 1, există integrale ale funcției e*** peste pătratele indicate, deci valoarea integralei cerute §4. Modificarea variabilelor într-o integrală dublă 4.1. Conceptul de coordonate curbilinie ale unui punct Să fie dată o pereche de funcții în regiunea D* a planului uOv, pe care o vom considera continuă în această regiune și având derivate parțiale continue. În virtutea ecuației (1), fiecare punct M*(α, v) al domeniului D* corespunde unui punct specific M(x, y) în planul xOy, și astfel punctele domeniului D* corespund unui un anumit set D de puncte (x, y) în planul xOy (Fig. 13). În acest caz, ei spun că funcțiile (1) mapează domeniul D4 pe mulțimea D. Să presupunem că diferite puncte (u, v) corespund diferitelor puncte (x, y). Aceasta este echivalentă cu solubilitatea unică a ecuațiilor (1) în raport cu u, v: în acest caz, maparea se numește o mapare unu-la-unu a domeniului D* pe domeniul D. Cu o astfel de transformare, orice curba continuă L* aflată în domeniul D* se va transforma într-o curbă continuă L situată în regiunea D. Dacă funcțiile d(x) y) și h(x, y) sunt de asemenea continue, atunci orice linie continuă LCD cu ajutorul de transformare (2) va trece pe linia continuă L* C D*. Pentru o pereche dată Ш, Vo valori ale variabilelor și, v din regiunea D*, este posibil să se determine fără ambiguitate nu numai poziția punctului M*(u<)> Vq) în regiunea £)* însăși, dar poziția punctului corespunzător M(xo, vo) în regiunea D, xo = 4>(io, v0), 3/0 = o, vo). Acest lucru dă motive pentru a considera numerele u, v ca niște coordonate noi ale punctului D al regiunii M pe planul xOy. Ele se numesc coordonate curbilinii ale punctului M. Mulțimea punctelor din zona D pentru care una dintre coordonate rămâne constantă se numește linie de coordonate. Fixând u = vq în formula (1), se obțin ecuații parametrice ale dreptei de coordonate.Aici rolul parametrului este jucat de variabila u. Dând coordonatei v diverse (posibile pentru aceasta) valori constante, obținem o familie de drepte de coordonate (v = const) pe planul xOy. În mod similar, obținem o altă familie de drepte de coordonate (u = const). Dacă există o corespondență unu-la-unu între regiunile D* și D, linii de coordonate diferite ale aceleiași familii nu se intersectează, iar o linie din fiecare familie trece prin orice punct al regiunii D. Grila de linii de coordonate curbilinii pe planul xOp este o imagine a unei grile dreptunghiulare pe planul uOv (vezi Fig. 13). 4.2. Element de zonă în coordonate curbilinie. Jacobianul și semnificația lui geometrică Să selectăm în regiunea D* pe planul Uo*V un dreptunghi mic P*P?P$Pl cu laturile paralele cu axele de coordonate 0*u și O"v și lungimile laturilor Ai și Av. (pentru certitudine, presupunem că respectiv A ) (Fig. 14 a). Aria sa Dreptunghi se transformă într-un patrulater curbiliniu * în zona D (Fig. 146). Dacă vârfurile P) au coordonate, atunci, după formulele (1). ), vârfurile corespunzătoare Pi au coordonate), Folosind formula lui Taylor pentru o funcție a două variabile și limitându-ne la termeni de ordinul întâi/pc relativ la A și Av, obținem următoarele valori aproximative ale coordonatelor pentru vârfurile unui patrulater unde funcţiile şi toate derivatele lor sunt calculate în punct).Expresiile găsite pentru coordonatele punctelor arată că, până la patrulaterul mic de ordin superior P\PiPiPa este un paralelogram.Aceasta rezultă din faptul că Atunci aria DS a lui patrulaterul poate fi exprimat aproximativ în termeni de lungime a produsului vectorial, Problemă care duce la conceptul de integrală dublă Definiția integralei duble Proprietăți de bază ale integralei duble Aria unei regiuni plane Reducerea integralei duble la repetat unul Înlocuirea variabilelor în integrală dublă Element de zonă în coordonatele curbilinii Jacobian și semnificația sa geometrică Formula pentru modificarea variabilelor în integrală dublă Integrală dublă în coordonate polare Determinant Din formulele (7) și (8) ale videoclipului, valoarea absolută a jacobianului joacă rolul unui coeficient de întindere local al regiunii D" (în acest punct (tx, v)) atunci când îl mapați pe domeniul D folosind formulele de transformare (1). 4.3. Formula pentru schimbarea variabilelor într-o integrală dublă Fie că funcțiile continue efectuează o mapare unu-la-unu a domeniului D* pe D și au derivate parțiale continue de ordinul întâi. Să fie dată o funcție continuă într-o regiune D pe planul xOy. Fiecare valoare a funcției) din regiunea D corespunde unei valori egale a funcției r = în regiunea D", unde. Să împărțim regiunea D* în regiuni parțiale și construiți o partiție corespunzătoare a regiunii D. Selectați puncte în regiunile parțiale corespunzătoare (u, v) și (x, y) astfel încât valorile funcțiilor din ele să coincidă și compunem sume integrale pentru funcțiile z = /(x, y) și v) pe domeniile D și D*.Obținem jacobianul funcțiilor.Mergând la egalitatea (9) la limita ca cel mai mare diametru d* al regiunilor parțiale D\ tinde la zero (datorită continuității hărții (I), cel mai mare dintre diametrele d ale regiunilor parțiale din D va tinde spre zero), vom avea unde Condiția J Ф 0 este condiția mapare locală unu-la-unu efectuată prin funcțiile Teorema 4. Pentru a transforma integrala dublă specificată în coordonate carteziene într-o integrală dublă în coordonate curbilinie, este necesară înlocuirea variabilelor x și y în funcția integrandă /(x, y) respectiv prin arie element dx dy - exprimarea lui în coordonate curbilinie: Exemplu. Aflați aria unei figuri mărginite de hiperbole m. Găsirea ariei figurii indicate se reduce la calcularea integralei duble asupra regiunii O. Să introducem coordonate noi, curbilinii și și o prin formulele Din condiția a ecuației, că. Aceasta înseamnă că în planul uOv am obținut un dreptunghi (Fig. 156) - o figură mai simplă decât figura dată D. Să exprimăm x și y din relațiile (11) prin u și t>: Fig. 15 Apoi integrală dublă în coordonate polare Calculul integralei duble este adesea simplificat prin înlocuirea coordonatelor dreptunghiulare x și y cu coordonate polare conform formulelor Elementul zonă în coordonate polare are forma și formula pentru trecerea de la integrala în coordonate carteziene la integrala în coordonate polare. coordonatele polare pot fi scrise astfel: În acest caz (13) Elementul de zonă în coordonate polare poate fi obținut și din considerente geometrice (vezi Fig. 16). Aria zonei umbrite din figura A = pl. sectoare. sectoare Renunțând la cantitatea infinitezimală de ordin superior, o obținem și o luăm ca element de zonă în coordonate polare. Deci, pentru a transforma o integrală dublă în coordonate carteziene într-o integrală dublă în coordonate polare, trebuie să înlocuiți a: și y în integrand, respectiv, prin p costp și psiny, și să înlocuiți elementul de zonă în coordonatele carteziene dx dy cu elementul zonă în coordonate polare p dp dip. Să începem acum să calculăm integrala dublă în coordonate polare. Ca și în cazul coordonatelor carteziene dreptunghiulare, calculul integralei în coordonate polare se realizează prin reducerea acesteia la o integrală iterată. Să luăm mai întâi în considerare cazul în care polul O se află în afara unei anumite regiuni D. Fie regiunea D să aibă proprietatea că orice rază care emană din pol (linia de coordonate y intersectează limita sa în cel mult două puncte sau de-a lungul unui întreg segment). (Fig. 17).Rețineți că valorile extreme i ale unghiului polar sunt limitele integrării externe.Raza μ> = trece prin punctul A al conturului regiunii D, iar raza prin punctul B. Punctele Aw B Împărțiți conturul regiunii D în două părți: ACB și AFB Fie ecuațiile lor polare și) sunt funcții continue cu o singură valoare care îndeplinesc condiția Funcțiile sunt limitele integrării interne. Trecând la integrale repetate, obținem următoarea formulă.În special, pentru aria S a regiunii D cu F(p, r 1 obținem Fie acum polul O situat în interiorul regiunii D. Să presupunem că regiunea D este stelar în raport cu polul, adică orice rază tp = const intersectează limita regiunii într-un singur punct sau de-a lungul unui întreg segment (Fig. 18). Fie ecuația limitei regiunii în coordonate polare. Atunci Fig. 18 Exemplu.Calculează integrala unde regiunea este un sfert din cercul unitar situat în primul cadran.Să trecem la coordonatele polare Atunci domeniul de integrare va fi un dreptunghi Integrala transformată / se calculează ușor: d Notă: Dacă Jacobianul este diferit de zero în domeniul D, atunci maparea într-o anumită vecinătate a fiecărui punct din acest domeniu este unu-la-unu. Totuși, se poate întâmpla ca maparea întregului domeniu să nu fie unu-la-unu. Să luăm în considerare maparea definită de funcții.Jacobianul acestor funcții este egal și, prin urmare, peste tot diferit de zero. Indiferent, obținem pentru, așa că această mapare nu este unu-la-unu. Pe de altă parte, dacă jacobianul unei mapări dispare la un moment dat, atunci, totuși, maparea într-o vecinătate a acestui punct se poate dovedi a fi unu-la-unu. De exemplu, pentru o mapare definită de funcții, Jacobianul este egal cu zero și la, dar maparea este unu-la-unu. Maparea inversă este determinată de funcții

1.1 Definiția integralei duble

1.2 Proprietăți ale integralei duble

Proprietățile unei integrale duble (și derivarea lor) sunt similare cu proprietățile corespunzătoare ale unei singure integrale definite.

1°. Aditivitate. Dacă funcția f(x, y) este integrabilă într-o regiune D și dacă regiunea D este împărțită de o curbă Г de zonă zero în două regiuni conexe D1 și D2 care nu au puncte interne comune, atunci funcția f(x , y) este integrabil în fiecare din zonele D 1 și D 2, și

2°. Proprietate liniară. Dacă funcțiile f(x, y) și g(x, y) sunt integrabile în domeniul D, nu? Și? - orice numere reale, apoi funcția [? · f(x, y) + ?· g(x, y)] este de asemenea integrabil în domeniul D și

3°. Dacă funcțiile f(x, y) și g(x, y) sunt integrabile în domeniul D, atunci produsul acestor funcții este de asemenea integrabil în D.

4°. Dacă funcțiile f(x, y) și g(x, y) sunt ambele integrabile în domeniul D și peste tot în acest domeniu f(x, y) ? g(x, y), atunci

5°. Dacă funcția f(x, y) este integrabilă în domeniul D, atunci funcția |f(x, y)| integrabil în domeniul D și

(Desigur, integrabilitatea lui |f(x, y)| în D nu implică integrabilitatea lui f(x, y) în D.)

6°. Teorema valorii medii. Dacă ambele funcții f(x, y) și g(x, y) sunt integrabile într-un domeniu D, funcția g(x, y) este nenegativă (nepozitivă) peste tot în acest domeniu, M și m sunt supremul şi infimul funcţiei f( x, y) în domeniul D, atunci există un număr? care satisface inegalitatea m ? ? ? M și astfel încât formula să fie validă

În special, dacă funcția f(x, y) este continuă în D și domeniul D este conex, atunci în acest domeniu există un punct (?, ?) astfel încât? = f(?, ?), iar formula ia forma

7°. Proprietate geometrică importantă. egal cu suprafața regiunii D

Fie dat un corp T în spațiu (Fig. 2.1), mărginit de jos de regiunea D, de sus - de graficul unei funcții continue și nenegative) z=f (x, y), care este definit în regiunea D, din laturi - printr-o suprafață cilindrică, al cărei ghid este regiunea de limită D, iar generatoarele sunt paralele cu axa Oz. Un corp de acest tip se numește corp cilindric.

1.3 Interpretarea geometrică a integralei duble

1.4 Conceptul de integrală dublă pentru un dreptunghi

Fie definită o funcție arbitrară f(x, y) peste tot pe dreptunghiul R = ? (vezi fig. 1).

Să împărțim segmentul a? X? b în n segmente parțiale folosind punctele a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

Această împărțire folosind linii drepte paralele cu axele Ox și Oy corespunde împărțirii dreptunghiului R în n · p dreptunghiuri parțiale R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Notăm partiția indicată a dreptunghiului R prin simbolul T. În continuare, în această secțiune, termenul „dreptunghi” va fi înțeles ca un dreptunghi cu laturile paralele cu axele de coordonate.

Pe fiecare dreptunghi parțial R kl alegem un punct arbitrar (? k, ? l). Punând?x k = x k - x k-1, ?y l = y l - y l-1, notăm cu?R kl aria dreptunghiului R kl. Evident, ?R kl = ?x k ?y l .

se numește suma integrală a funcției f(x, y) corespunzătoare unei partiții date T a dreptunghiului R și unei alegeri date de puncte intermediare (? k, ? l) pe dreptunghiurile parțiale ale partiției T.

Vom numi diagonala diametrul dreptunghiului R kl. Un simbol? să notăm cel mai mare dintre diametrele tuturor dreptunghiurilor parțiale cu R kl .

Numărul I se numește limita sumelor integrale (1) la? > 0 dacă pentru orice număr pozitiv? poti specifica un astfel de numar pozitiv?, ce daca?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - eu |< ?.

O funcţie f(x, y) se numeşte Riemann integrabilă pe un dreptunghi R dacă există o limită finită I a sumelor integrale ale acestei funcţii la? > 0.

Limita specificată I se numește integrală dublă a funcției f(x, y) peste dreptunghiul R și se notează cu unul dintre următoarele simboluri:

Cometariu. La fel ca pentru o integrală unică definită, se stabilește că orice funcție f(x, y) integrabilă pe un dreptunghi R este mărginită pe acest dreptunghi.

Acest lucru oferă motive de luat în considerare în cele ce urmează doar funcții limitate f(x, y).

O problemă care duce la conceptul de integrală dublă.

Să presupunem că funcția părților este definită și notează suma

care se numește integrală.

R: Sub integrala definită (d.i.) a funcției și a alegerii

Desemnare:

Numerele se numesc Riemann integrabile pe .

T. existenţa: Cu condiţia ca .

În conformitate cu definiția o.i. observăm că integrala depinde de tip, limite și, dar nu depinde de simbolul desemnării variabilei, altfel exprimat

În conformitate cu clauzele 17.1.1 și 17.1.2 și cu definiția o.i. Să scriem formula pentru aria unui trapez curbiliniu: , munca de forta

pe :

Conceptul de integrală dublă, sume integrale.

Existența unei integrale duble, adică o limită a sumei integrale pentru, pare evidentă, deoarece această limită dă volumul unui corp cilindric. Cu toate acestea, acest raționament nu este riguros. În cursurile mai complete, această afirmație este strict dovedită și se numește teorema existenței unei integrale duble.

Teorema existenței. Pentru orice funcție care este continuă într-o regiune închisă mărginită având aria a, există o integrală dublă, adică există o limită a sumelor integrale cu o creștere nelimitată a numărului de arii mici, cu condiția ca fiecare dintre ele să se contracte la o punct. Această limită nu depinde de metoda de împărțire a regiunii în părți sau de alegerea punctelor

În cele ce urmează vom lua în considerare numai funcțiile care sunt continue în domeniul integrării.

Din teorema existenței rezultă că putem, de exemplu, să împărțim regiunea a în dreptunghiuri mici cu laturile drepte paralele cu axele de coordonate (Fig. 230). în care. Apoi alegând un punct în fiecare dreptunghi mic, putem scrie, conform definiției integralei duble

Pentru a sublinia că integrala dublă poate fi obținută ca limită a unei sume a formei, în loc de notație, folosim și notația

Expresia se numește element de zonă în coordonate carteziene și este egală cu aria unui dreptunghi cu laturile paralele cu axele de coordonate.

Rețineți că la compilarea sumei integrale, zonele adiacente graniței zonei a nu au forma dreptunghiurilor. Cu toate acestea, se poate dovedi că eroarea de la înlocuirea unor astfel de zone cu dreptunghiuri cu zone în limită va fi redusă la zero.

Proprietățile integralelor duble

Proprietățile unei integrale duble (și derivarea lor) sunt similare cu proprietățile corespunzătoare ale unei singure integrale definite.

3°. Dacă funcţiile f(X, y) Și g(X, y) sunt integrabile în domenii D, atunci produsul acestor funcții este integrabil în D.

4°. Dacă funcţiile f(X, y) Și g(X, y) ambele sunt integrabile în domeniul Dși peste tot în această zonă f(X, y) ≤ g(X, y), Acea

5°. Dacă funcţia f(X, y) este integrabil în domeniu D, apoi funcția | f(X, y)| integrabil în zone D, și

(Desigur, din integrabilitate | f(X, y)| V D integrabilitatea nu urmează f(X, y) V D.)

În special, dacă funcția f(X, y) este continuă în D, și zona D coerent, atunci în această regiune există un astfel de punct ( ξ , η ), Ce μ = f(ξ , η ), iar formula (11) ia forma

Pentru o funcție a două variabile specificate ca z = f(X, y) .

Integrala dubla se scrie astfel:

Aici D– o figură plată mărginită de drepte, ale cărei expresii (egalități) sunt date în sarcina de a calcula integrala dublă. Stânga și dreapta sunt egalități în care se află variabila din stânga X, iar deasupra și dedesubt – prin egalități în care se află variabila din stânga y. Acest loc continuă să fie unul dintre cele mai importante pentru înțelegerea tehnicii de calcul a integralei duble.

Calculați integrală dublă - înseamnă găsirea unui număr egal cu aria figurii menționate D .

Până ne atingem definiții duble integrale , și vom învăța să o calculăm. Este mai ușor de înțeles ce este o integrală dublă atunci când ai rezolvat mai multe probleme pentru a o calcula, așa că vei găsi definiția unei integrale duble la sfârșitul acestei lecții. Privind puțin înainte, putem doar să remarcăm că definiția unei integrale duble este legată și de figura menționată D .

Dacă cifra D este un dreptunghi, toate liniile care îl limitează sunt drepte. Dacă cifra D- este curbiliniu, apoi în stânga și în dreapta este limitat de linii drepte, iar deasupra și dedesubt de linii curbe, date de egalitățile care sunt date în sarcină. Există, de asemenea, cazuri când o cifră D- un triunghi, dar mai mult pe astfel de cazuri un pic mai departe.

Pentru a calcula integrala dublă, este deci necesar să sortați liniile care mărginesc figura D, care are un nume strict - regiunea de integrare. Sortați în stânga și dreapta și sus și jos. Acest lucru va fi necesar când reducerea unei integrale duble la o integrală iterată – metoda de calcul a integralei duble.

Cazul unei zone dreptunghiulare:

Cazul unei regiuni curbe:

Și aceasta este deja o soluție la integralele definite familiare, în care sunt date limitele superioare și inferioare ale integrării. Expresii care definesc linii care delimitează o figură D, vor fi limitele integrării pentru integralele definite obișnuite, de care ne apropiem deja.

Reducerea unei integrale duble la una repetată

Cazul unei regiuni dreptunghiulare

Să existe o integrală dublă pentru o astfel de funcție

La evaluați această integrală dublă , trebuie să o reducem la o integrală iterată, care are forma

Mai întâi trebuie să calculați integrala definită interioară (dreapta), apoi integrala definită exterioară (stânga).

Puteți schimba rolurile XȘi y

Exemplul 1. Calculați integrală dublă

Calculăm integrala interioară (dreapta), considerând y ca o constantă. Am luat.

Exemplul 2. Calculați integrală dublă

Soluţie. Reducem această integrală dublă la o integrală iterată

În desen construim regiunea de integrare:

Acum calculăm integrala exterioară (stânga) a interioarei (dreapta) tocmai calculată:

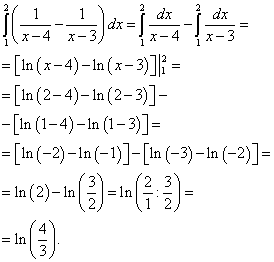
Rezultatul va fi soluția acestei integrale duble.

Calculați singur integrala dublă și apoi uitați-vă la soluție

Cazul unei regiuni curbe sau triunghiulare

Să ne dăm din nou o funcție a două variabile f(X, y) , și restricțiile pentru D: deja de un tip ușor diferit:

Această intrare înseamnă că cifra D stânga și dreapta sunt limitate, ca în cazul unei regiuni rectilinie - linii drepte X = AȘi X = b, dar mai jos și deasupra sunt curbe care sunt date de ecuațiile și . Cu alte cuvinte, și sunt funcții.

Fie ca o astfel de funcție să aibă și o integrală dublă

Pentru a evalua această integrală dublă, trebuie să o reducem la o integrală iterată, care are forma

Iată limitele integrării AȘi b- numere și și - funcții. În cazul unei regiuni triunghiulare, una dintre funcțiile sau este ecuația unei drepte. Acest caz va fi discutat în Exemplul 3.

Ca și în cazul unei regiuni rectilinie, mai întâi trebuie să calculați integrala definită dreaptă, apoi integrala definită stânga.

În același mod, puteți schimba rolurile XȘi y. Atunci integrala repetată va avea forma

O astfel de integrală repetată trebuie rezolvată exact în același mod: mai întâi - integrala interioară (dreapta), apoi - cea exterioară (stânga).

Exemplul 5. Calculați integrală dublă

Soluţie. Reducem această integrală dublă la o integrală iterată

În desen construim regiunea de integrare și vedem că este triunghiulară:

Calculăm integrala interioară (dreapta), considerând x o constantă. Am luat.

Acum calculăm integrala exterioară (stânga) a interioarei (dreapta) tocmai calculată. Mai întâi prezentăm această integrală ca o sumă de integrale:

Calculăm primul termen:

Calculăm al doilea termen:

Calculăm al treilea termen:

Obținem suma, care va fi soluția acestei integrale duble:

Exemplul 6. Calculați integrală dublă

Soluţie. Reducem această integrală dublă la o integrală iterată

În desen construim regiunea de integrare:

Calculăm integrala interioară (dreapta), considerând x o constantă. Am luat.

Acum calculăm integrala exterioară (stânga) a interioarei (dreapta) tocmai calculată:

Rezultatul va fi soluția acestei integrale duble.

X-bine si rau y-domenii corecte şi incorecte de integrare

Se întâmplă ca domeniul de integrare al unei integrale duble să fie limitat de astfel de linii încât devine necesar să se împartă domeniul de integrare în părți și să se rezolve separat fiecare integrală repetată corespunzătoare. Acestea sunt cazurile când:

1) zona de integrare este o figură care are două sau mai multe linii drepte sau curbe sub forma unei granițe inferioare sau superioare (stânga sau dreaptă);

2) regiunea de integrare este o figură a cărei graniță liniile se intersectează în mai mult de două puncte.

Dacă cele de mai sus se aplică graniței din stânga sau din dreapta a domeniului de integrare, adică restricțiile definite de liniile exprimate în termeni de X, atunci se numește domeniul integrării X-gresit. Dacă linia y = y0 intersectează granița corespunzătoare într-un singur punct, iar dacă granița este doar o singură linie dreaptă sau curbă, atunci domeniul de integrare se numește X-corect

În mod similar, dacă granița definită prin linii exprimate prin y, Drept X = X0 se intersectează în mai mult de un punct sau dacă granița este mai mult de o dreaptă sau curbă, atunci domeniul de integrare se numește y-gresit. Acum afișați semnele y- zona corectă, probabil, este destul de simplă.

Până acum ne-am uitat la exemple cu X-incorect și y-zone corecte de integrare. Acum luați în considerare cazurile în care condiția de corectitudine este încălcată.

Exemplul 7. Calculați o integrală dublă al cărei domeniu de integrare este limitat de linii y = X , X y = 1 , y = 2 .

Soluţie. Domeniul integrării este y-incorect, deoarece limita sa inferioară nu poate fi specificată de o singură linie y = y(X) . După cum se poate vedea în figura de mai sus, limita inferioară este formată din y = X(visiniu închis) și X y= 1 (verde). Prin urmare direct X= 1 (negru) putem împărți domeniul de integrare în două părți - și .

Această integrală dublă se calculează după cum urmează:

Schimbarea ordinii de integrare

După cum sa menționat mai sus, după reducerea integralei duble la o integrală iterată, puteți modifica variabilele XȘi y roluri sau, cu alte cuvinte, schimba ordinea integrării.

Schimbarea în ordinea integrării poate fi descrisă figurativ prin următoarele cuvinte ale lui O'Henry: „Așa se comportă un locuitor al junglei - un animal - când intră într-o cușcă și așa este un locuitor în cușcă - un om - se comportă atunci când se pierde în jungla îndoielilor.” Rezultatul, potrivit lui O’Henry, este același și același: „Chalmers a rupt scrisoarea în o mie de bucăți mici și a început să-și rupă covorul scump, mergând înapoi și mai departe pe ea.” ( O.Henry. Scheherazada din Madison Square.)

Atunci, dacă integrala noastră stângă peste variabilă X, iar cel potrivit - de y, apoi după schimbarea ordinii de integrare totul va fi invers. Atunci limitele de integrare pentru jocul „noul” trebuie „împrumutate” de la „vechiul” X, iar limitele de integrare pentru „noul” X trebuie obținute sub forma funcție inversă, rezolvând pentru x ecuația care stabilește limita pentru y.

Exemplul 8.

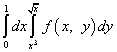Soluţie. După schimbarea ordinii de integrare, integrala peste y va deveni stângaci, iar integrala peste x va deveni dreapta. Vom împrumuta limitele de integrare pentru jocul „noul” de la „vechiul” X, adică limita inferioară este egală cu zero, iar limita superioară este egală cu unu. Limitele de integrare pentru jocul „vechi” sunt date de ecuațiile și . După rezolvarea acestor ecuații pentru x, obținem noi limite de integrare pentru x:

(inferioară) și (superioară).

Astfel, după schimbarea ordinii de integrare, integrala repetată se va scrie astfel:

După schimbarea ordinii integrării într-o integrală dublă, domeniul integrării se transformă adesea în y-incorect sau X-incorect (vezi paragraful anterior). Apoi, trebuie să împărțiți domeniul de integrare în părți și să rezolvați separat fiecare integrală iterată corespunzătoare.

Întrucât împărțirea domeniului integrării în părți prezintă anumite dificultăți pentru mulți studenți, nu ne vom limita la exemplul dat în paragraful anterior, ci vom mai analiza câteva exemple.

Exemplul 9. Schimbați ordinea integrării pentru integrala iterată

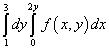Soluţie. Deci, aria de integrare a acestei integrale iterate este limitată de linii drepte y = 1 , y = 3 , X = 0 , X = 2y .

Când se integrează într-o ordine diferită, limita inferioară a regiunii constă din două linii drepte: ABȘi B.C., care sunt date de ecuații y= 1 și y = X/2, după cum se poate vedea în figura de mai jos.

Calea de ieșire dintr-o astfel de incertitudine este împărțirea domeniului de integrare în două părți. Împărțirea domeniului de integrare va fi o linie dreaptă BM. Calculăm noi limite de integrare prin găsirea funcției inverse. Conform acestei soluții, integrala repetată după schimbarea ordinii de integrare va fi egală cu suma a două integrale:

Desigur, aceeași va fi și soluția integralei duble, care se reduce la integrala repetată dată în condiția acestui exemplu.

Exemplul 10. Schimbați ordinea integrării pentru integrala iterată

Soluţie. Deci, domeniul de integrare al integralei iterate este limitat la linii drepte X = 0 , X= 2 și curbele și .

După cum se poate vedea în figura de mai jos, o linie dreaptă paralelă cu axa 0x, va intersecta limita inferioară a domeniului de integrare în mai mult de două puncte.

Prin urmare, împărțim domeniul de integrare în trei părți prin linii drepte, care sunt desenate cu negru în figură. Calculăm noi limite de integrare prin găsirea funcției inverse. Limitele pentru cele trei noi domenii de integrare vor fi următoarele.

Conform acestei soluții, integrala repetată după schimbarea ordinii de integrare va fi egală cu suma a trei integrale:

Aceeași sumă a trei integrale va fi egală cu integrala dublă, care se reduce la integrala repetată dată în condiția acestui exemplu.

Și totuși, circumstanțele de forță majoră interferează adesea cu studenții aflați deja la pasul anterior - stabilirea limitelor integrării. Anxietatea și confuzia nu sunt lipsite de o anumită bază: dacă pentru a împărți regiunea de integrare în părți, este de obicei suficient să te uiți îndeaproape la desen și să rezolvi integrala repetată - tabelul integralelor, atunci este nevoie de ceva experiență de pregătire în stabilirea limitelor. de integrare. Să trecem printr-un exemplu în care ne vom concentra doar pe stabilirea limitelor integrării și - aproape automat - pe partiționarea regiunii și să omitem soluția în sine.

Exemplul 11. Aflați limitele de integrare a unei integrale duble dacă domeniul integrării D dat după cum urmează:

y - 2X ≤ 0;
2 ani - X ≥ 0;
X y ≤ 2.

Soluţie. În mod explicit (via XȘi y„fără impurități”) nu sunt specificate liniile care limitează regiunea de integrare. Deoarece pentru X ele se dovedesc cel mai adesea a fi linii drepte care ating la un moment dat limitele superioare și inferioare, exprimate prin i, atunci vom merge exact pe această cale. Mai mult, la schimbarea ordinii de integrare, obținem o regiune de integrare cu aceeași zonă. Să rezolvăm inegalitățile pentru joc și să obținem:

y ≤ 2X;
y ≥ X/2;
y ≤ 2/X.

Construim liniile rezultate pe desen. Limitele integrării peste x sunt într-adevăr liniile X= 0 și X= 2 . Dar zona de integrare s-a dovedit a fi y-incorect, deoarece limita sa superioară nu poate fi specificată de o singură linie y = y(X) .

Ar putea fi util să citiți: