Çift katlı integralin temel özellikleri. Çift katlı integral problem tanımı Çift katlı integralin temel özellikleri Çift katlı integral temel kavramlar ve tanımlar
Çift katlı integralin temel özellikleri
Çift katlı bir integralin özellikleri (ve bunların türetilmesi), tek bir belirli integralin karşılık gelen özelliklerine benzer.
1°. toplanabilirlik. Eğer fonksiyon F(X, sen) etki alanında entegre edilebilir D ve eğer alan D bir eğri kullanma G sıfır alanı ortak iç noktaları olmayan iki bağlantılı bölgeye bölünmüştür D 1 ve D 2, ardından fonksiyon F(X, sen) her bir alana entegre edilebilir D 1 ve D 2 ve
2°. Doğrusal özellik. Eğer işlevler F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, A α Ve β - herhangi bir gerçek sayı, ardından fonksiyon [ α · F(X, sen) + β · G(X, sen)] ayrıca etki alanında entegre edilebilir D, Ve
3°. Eğer işlevler F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, o zaman bu fonksiyonların çarpımı şu şekilde integrallenebilir: D.
4°. Eğer işlevler F(X, sen) Ve G(X, sen) her ikisi de etki alanıyla entegre edilebilir D ve bu bölgenin her yerinde F(X, sen) ≤ G(X, sen), O
5°. Eğer fonksiyon F(X, sen) etki alanında entegre edilebilir D, ardından işlev | F(X, sen)| alanlara entegre edilebilir D, Ve
(Elbette entegre edilebilirlikten | F(X, sen)| V D entegre edilebilirlik takip etmiyor F(X, sen)V D.)
6°. Ortalama değer teoremi. Her iki işlev de varsa F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, işlev G(X, sen) bu bölgenin her yerinde negatif değildir (pozitif değildir), M Ve M- fonksiyonun tam üst ve tam alt sınırları F(X, sen) bölgede D, o zaman bir sayı var μ eşitsizliğin sağlanması M ≤ μ ≤ M ve formülün geçerli olduğu şekilde
Çift katlı integral kavramına yol açan problem Çift katlı integralin tanımı Çift katlı integralin temel özellikleri Düz bölgenin alanı Çift katlı integralin tekrarlı integrale indirgenmesi Çift katlı integralde değişkenlerin değişimi Eğrisel koordinatlarda alan elemanı Jacobian ve geometrik anlamı Çift katlı integralde değişkenlerin değişiminin formülü Kutupsal koordinatlarda çift katlı integral


















Çift katlı integral kavramına yol açan bir problem. Çift katlı integralin tanımı. Silindirik bir cismin hacminin hesaplanmasına ilişkin özel problemi çözerek çift katlı integral kavramına ulaşıyoruz. Silindirik bir gövde, xOy düzlemi, belirli bir yüzey ve genatrileri eksene paralel olan silindirik bir yüzey tarafından sınırlanan bir gövdedir (bkz. Şekil 1). X ve y değişkenlerindeki değişimin olduğu D bölgesine silindirik cismin tabanı denir. Bir cismin hacmini belirlerken iki prensipten yola çıkacağız: !) eğer cismi parçalara ayırırsak, o zaman hacmi tüm parçaların hacimlerinin toplamına eşittir (toplanabilirlik özelliği); 2) xOy düzlemine paralel z = const düzlemiyle sınırlanan düz bir silindirin hacmi, taban alanının yükseklikle çarpımına eşittir. Aşağıda D bölgesinin bağlantılı (tek parçadan oluştuğu), karelenebilir (yani bir alana sahip) ve sınırlı (yani orijin merkezli belirli bir dairenin içinde yer aldığını) varsayacağız. Z> bölgesinin her yerinde P(x, y) noktasının sürekli bir fonksiyonu olsun, yani söz konusu silindirik yüzey tamamen xOy düzleminin üzerinde olsun. Silindirik bir cismin hacmini V ile gösterelim. D bölgesini (silindirik cismin tabanı) belirli sayıda n adet kesişmeyen, keyfi şekle sahip dörtlü bölgelere böleriz; bunlara kısmi bölgeler diyeceğiz. Kısmi alanları belirli bir sıraya göre numaralandırdıktan sonra alanlar buna göre numaralandırılır. Kısmi bir bölgenin çapını Dk miktarı olarak adlandıralım Çift katlı integral kavramına yol açan problem Çift katlı integralin tanımı Çift katlı integralin temel özellikleri Düz bir bölgenin alanı Çift katlı integralin tekrarlı integrale indirgenmesi çift katlı integralde değişkenler Eğrisel koordinatlarda alan elemanı Jacobian ve geometrik anlamı Çift katlı integralde değişkenlerin değişimi için formül Kutupsal koordinatlarda çift katlı integral, burada p(P; Q), P ve Q noktaları arasındaki mesafe anlamına gelir. d ile kısmi bölgelerin çaplarının en büyüğü Dk (k = 1,2,..., n). Her kısmi bölgenin sınırı boyunca jeneratörlerin Oz eksenine paralel olduğu silindirik bir yüzey çizelim. Sonuç olarak, silindirik gövde n adet kısmi silindirik gövdeye bölünecektir. Bu kısmi gövdeyi, değiştirilen yüzeyin herhangi bir noktasının uygulamasıyla aynı taban ve yüksekliğe sahip düz bir silindirle değiştirelim (Şekil 2). Böyle bir silindirin hacmi, noktanın Dk bölgesinin alanı olduğu yere eşittir. Her bir kısmi silindirik gövde için açıklanan yapıları gerçekleştirdikten sonra, hacmi (o) Sezgisel olarak, kısmi bölgelerin boyutu ne kadar küçük olursa, Vn'nin arzu edilen V hacmini daha doğru bir şekilde ifade ettiği açıktır. Dk. Silindirik bir cismin hacmini V, n-adımlı bir cismin hacminin (1) n-bin olarak yöneldiği limite eşit olarak alıyoruz ve Dk kısmi bölgelerinin en büyük çapı d, sıfıra yaklaşıyor. Doğal olarak limit, D bölgesinin Dk kısmi bölgelerine bölünme tipine ve kısmi bölgelerdeki Pk noktalarının seçimine bağlı olmamalıdır. /(x, y), D bölgesinde tanımlanan isteğe bağlı bir fonksiyon olsun. n(1) toplamına, bu tanım kümesinin belirli bir bölümüne karşılık gelen, D alanı üzerinde f(x)y) fonksiyonunun integral toplamı denir. n kısmi bölgeye ve Dk kısmi bölgeleri üzerindeki belirli bir nokta seçimi Ж ®*,!/*)'ye bölünür. Tanım. d -* 0 için, D alanını kısmi alanlara bölme yöntemine veya kısmi bölgelerde Pk noktalarının seçimine bağlı olmayan n integral toplamlarının bir limiti varsa, o zaman buna çift katlı integral denir. f(P) (veya f(x, y )) fonksiyonu D bölgesi üzerindedir ve OR sembolü ile gösterilir. Yani, (2) Fonksiyonun kendisi f(x, y) D bölgesinde integrallenebilir olarak adlandırılır (f( P) integraldir, f(P) dS integraldir, dS alanın diferansiyelidir (veya elemanı), D bölgesi - entegrasyon bölgesi; P(®, y) noktası - entegrasyonun değişken inceliği). ,.. Silindirik cisme dönersek şu sonuca varırız: xOy düzlemi, yüzey ve generatrisleri Oz eksenine paralel olan silindirik bir yüzey tarafından sınırlanan silindirik bir cismin hacmi, fonksiyonun çift katlı integraline eşittir /( x, y) silindirik gövdenin tabanı olan D bölgesi üzerinde. / VEYA Burada dx dy Kartezyen koordinatlardaki alan elemanıdır. Bu, negatif olmayan bir fonksiyonun çift katlı integralinin geometrik anlamıdır. Eğer f(P) fonksiyonunun D bölgesindeki If hacmi hem pozitif hem de negatif değerler alıyorsa, bu durumda integral, xOy düzleminin üzerinde yer alan gövde parçalarının hacimlerinin cebirsel toplamını temsil eder (şu şekilde alınır: “+” işareti) ve vücudun xOy düzleminin altında bulunan kısımları (“-” işaretiyle alınır). Sadece silindirik bir cismin hacmi problemi değil, çok çeşitli problemler, iki bağımsız değişkenin bir fonksiyonu için (1) formunun toplamlarının derlenmesine ve daha sonra limite geçişe yol açar. İntegrallenebilirlik için yeterli koşulları formüle edelim. Teorem 1. Sınırlı kapalı bir D bölgesinde sürekli olan herhangi bir y) fonksiyonu bu bölgede integrallenebilir. İntegralin devamlılığı gerekliliği çoğu zaman çok kısıtlayıcı olur. Uygulamalar için, belirli bir süreksiz fonksiyon sınıfı için çift katlı integralin varlığını garanti eden aşağıdaki teorem önemlidir. Düzlemdeki belirli bir nokta kümesinin alanı keyfi olarak küçük bir çokgen şekil içine alınabiliyorsa sıfır alana sahip olduğunu söyleyeceğiz. Teorem 2. Eğer bir /(x, y) fonksiyonu kapalı sınırlı bir D kümesinde sınırlıysa ve sıfır alanının bazı noktaları dışında D'nin her yerinde sürekliyse, o zaman bu fonksiyon D kümesinde integrallenebilir. §2. Çift katlı integralin temel özellikleri Çift katlı integraller, tek bağımsız değişkenli fonksiyonlar için belirli integralin özelliklerine benzer bir dizi özelliğe sahiptir. 2.1. Doğrusal özellik Eğer fonksiyonlar) D bölgesinde integrallenebilirse ve a ve p herhangi bir gerçek sayıysa, o zaman af) fonksiyonu da D bölgesinde integrallenebilirdir ve o) 2.2. Eşitsizliklerin integrali Eğer fonksiyonlar) D alanında ve bu alanın her yerinde integrallenebilirse, o zaman (2) yani eşitsizlikler entegre edilebilir. Özellikle, elde ettiğimiz bariz eşitsizlikleri entegre ederek Düz bir bölgenin alanı Düz bir D bölgesinin alanı, bire eşit bir fonksiyonun bu bölgesi üzerindeki çift katlı integraline eşittir. Gerçekte, D alanındaki /(P) = 1 fonksiyonunun integral toplamı şu şekildedir ve D alanının Dt kısmi alanlarına herhangi bir bölümü için S alanına eşittir. Ancak bu durumda bu toplamın limiti, yani çift katlı integral S alanına eşittir D: veya aynısı (3) 2.4. İntegralin tahmini f(P) fonksiyonu sınırlı bir kapalı D bölgesinde sürekli olsun, M ve mn, f(P)'nin D alanındaki ve 5 alanındaki en büyük ve en küçük değerleri olsun. O halde (4) 2.5. Toplanabilirlik: Eğer /(P) fonksiyonu D bölgesinde integrallenebilirse ve Z) alanı, ortak iç noktalar olmaksızın iki D\ ve Di alanına bölünmüşse, bu durumda /(P), D\ ve Di alanlarının her birinde integrallenebilirdir ve (5) 2.6. Ortalama değer teoremi Teorem 3 (ortalama değer). /(P) fonksiyonu kapalı sınırlı bir D bölgesinde sürekli ise, o zaman D alanının en az bir Pc noktası vardır, öyle ki S'nin D alanının alanı olduğu formül geçerlidir. /(P) kapalı sınırlı bir D bölgesinde süreklidir, bu durumda D'de en büyük değeri M ve en küçük değeri m'yi alır. 4 özelliği ile sahip olduğumuz integralin tahminine göre, sayı en büyük ile en küçük arasında yer alır. D alanındaki /(P) fonksiyonunun değerleri. D alanındaki /( P) fonksiyonunun sürekliliği nedeniyle, Pc G D noktasında bu sayıya eşit bir değer alır, dolayısıyla S değeri f( Formül (7) ile belirlenen Pc), f(P) fonksiyonunun D bölgesindeki ortalama değeri olarak adlandırılır. Ortalama değer teoremi değerinin geometrik anlamı Eğer D bölgesinde /(P) ^ O fonksiyonu varsa, o zaman Formül (6), tabanı D (alanı 5 olan) ve yüksekliği H = /(Pc) olan, hacmi silindirik gövdenin hacmine eşit olan düz bir silindirin olduğu anlamına gelir (Şekil 1). 3). § 3. Çift katlı integrali yinelenen integrale indirgemek Çift katlı integrali hesaplamanın etkili yollarından biri, onu yinelenen integrale indirgemektir. 3.1. Dikdörtgen durumu D alanı, kenarları koordinat eksenlerine paralel olan kapalı bir P dikdörtgeni olsun. f(x, y) fonksiyonu P dikdörtgeninde sürekli olsun. Çift katlı integral, bir yüzeyle sınırlanan P tabanlı silindirik bir cismin (cebirsel) hacmi olarak yorumlanabilir. Karşılık gelen silindirik cismi düşünün. Oy eksenine dik bir düzlem çizelim (Şekil 4). Bu düzlem, silindirik gövdeyi yukarıdan denklemlerle tanımlanan düz bir z çizgisiyle sınırlanan eğrisel bir yamuk boyunca kesecektir. ABC\A yamuk alanı, entegrasyonun x ve yo üzerinde gerçekleştirildiği integral ile ifade edilir. - integralin ikinci argümanı - sabit olarak kabul edilir (c ^ Uo ^ d ). İntegralin (1) değeri, seçtiğiniz değere bağlıdır. (2) koyalım. İfade (2), silindirik bir cismin a kesit alanını y'nin bir fonksiyonu olarak verir. Dolayısıyla silindirik bir cismin hacmi şu formül kullanılarak hesaplanabilir. Öte yandan, bu hacim /(x, y) fonksiyonunun P dikdörtgeni üzerindeki çift katlı integrali ile ifade edilir. Bu, S(y)'nin yerine şunun yazılması anlamına gelir: ifadesini (2), elde ederiz Çift katlı integral kavramına yol açan problem Çift katlı integralin tanımı Çift katlı integralin temel özellikleri Düz bölgenin alanı Çift katlı integralin tekrarlı integrale indirgenmesi Çift katlı integralde değişkenlerin değiştirilmesi Eğrisel koordinatlarda alan elemanı Jacobian ve geometrik anlamı Çift katlı integralde değişkenlerin yer değiştirme formülü Kutupsal koordinatlarda çift katlı integral Son ilişki genellikle aşağıdaki şekilde yazılır Silindirik bir cismin hacmi aynı zamanda silindirik cismin kesit alanlarından da bulunabilir. düzlemler x = x0. Bu, formül (4)'e yol açar. Formül (3) ve (4)'ün sağ tarafındaki ifadelerin her biri, /(x, y) fonksiyonunun olağan integralinin iki ardışık işlemini içerir. Bunlara /(x, y) fonksiyonunun P bölgesi üzerindeki tekrarlı integralleri denir. Eğer f(x, y) kapalı bir P dikdörtgeninde sürekli ise, o zaman tekrarlı integrallere geçiş her zaman mümkündür ve (5) yani, Sürekli bir fonksiyonun /(x, y) tekrarlanan integrallerinin değerleri entegrasyon sırasına bağlı değildir. Örnek 1. Bir fonksiyonun elimizdeki bir tanım kümesi üzerindeki çift katlı integralini bulun (bkz. Şekil 5): 3.2. Keyfi bir alan durumu Şimdi, entegrasyon alanının, xOy düzlemi üzerinde, aşağıdaki koşulu sağlayan, keyfi olarak sınırlı, karelenebilir kapalı bir D alanı olduğunu varsayalım: Oy eksenine paralel herhangi bir düz çizgi, D bölgesinin sınırıyla hiçbir noktada kesişmez. iki noktadan fazla veya tüm segment boyunca (Şek. . 6a). Şekilde gösterildiği gibi D alanını dikdörtgenin içine alalım. 66. [a, 6] parçası, D bölgesinin Oksi ekseni üzerindeki dik izdüşümüdür ve [c, dj parçası, D bölgesinin Oy ekseni üzerindeki dik izdüşümüdür. A ve C noktaları D alanının sınırını iki ABC ve AEC eğrisine böler. Bu eğrilerin her biri Oy eksenine paralel rastgele bir düz çizgiyle birden fazla noktada kesişmez. Dolayısıyla denklemleri y'ye göre çözülmüş bir biçimde yazılabilir: f(x, y) D bölgesinde sürekli bir fonksiyon olsun. İncelenen silindirik cismi bir düzlemle parçalara ayıralım. Bu bölümde, alanı bir değişken y'nin fonksiyonu olarak kabul edilen /(x, y) fonksiyonunun sıradan integrali ile ifade edilen eğrisel bir yamuk PQMN (Şekil 7) elde ediyoruz. Bu durumda, y değişkeni P noktasının ordinatından Q noktasının ordinatına değişir\ nokta P, x = const (düzlemde) çizgisinin bölgeye "girişidir" - "çıkış" noktasıdır bu bölgeden. ABC eğrisinin denklemi ve eğri olduğundan, x için alınan bu ordinatlar sırasıyla eşittir. Sonuç olarak, integral bize kesme düzleminin konumunun bir fonksiyonu olarak silindirik bir gövdenin düz bir bölümünün alanı için bir ifade verir x = const. Tüm cismin hacmi bu ifadenin değişim aralığında x üzerinden integraline eşit olacaktır. Böylece, özellikle D bölgesinin S alanı için şunları elde ederiz: Şimdi her düz çizginin D bölgesinin sınırıyla apsisleri sırasıyla eşit olan en fazla iki P ve Q noktasında kesiştiğini varsayalım ( veya tüm segment boyunca) (Şek. 8). Benzer akıl yürütmeyi yürüterek, çift katlı integralin hesaplamasını da tekrarlanan bir hesaplamaya indirgeyen bir formüle ulaşıyoruz. Örnek 2. Bir fonksiyonun çizgilerle sınırlanan D alanı üzerindeki çift katlı integralini hesaplayın. ^ Birinci yöntem. D integralinin tanım kümesini gösterelim. y = x düz çizgisi ve y = x2 parabolünün kesiştiği noktalarda. Bu, x'in 0'dan 8 limit dahilinde değiştiği anlamına gelir. Herhangi bir x = const düz çizgisi, bölgenin sınırını en fazla iki noktada keser. Bu nedenle formül (8) uygulanabilir: İkinci yöntem (Şekil 10). Formül (10)'u kullanma. aynı sonucu elde ederiz: Örnek 3. Yarı eksenli bir elipsin çizgisi boyunca xOy düzlemiyle kesişen bir yüzeyle sınırlanan bir cismin hacmini, bu cismin xOz ve y Ox koordinat düzlemlerine göre simetrisinden dolayı hesaplayın. şunu elde ederiz: Not. D bölgesi, sınırlarını ikiden fazla noktada kesen bazı düz çizgiler (ostratekal veya yatay) ise, o zaman D bölgesi üzerindeki çift katlı integrali hesaplamak için, onu uygun şekilde parçalara ayırmalı, integrallerin her birini parçalar halinde tekrarlamalıyız. ve elde edilen sonuçları ekleyin. Örnek 4. Merkezi olan iki kare arasında, orijinde ve kenarları koordinat eksenlerine paralel olan D alanı üzerinde, içteki karenin bir kenarı 2 ve dıştaki kare 4 ise, çift katlı integrali hesaplayın. Bu, aşağıdaki gibi süreklidir. kenarı 4 olan büyük bir Q karesi ve kenarı 2'ye eşit olan küçük bir R karesi (Şekil 12). Teorem 1'e göre, e*** fonksiyonunun belirtilen kareler üzerindeki integralleri mevcuttur, dolayısıyla gerekli integralin değeri §4. Çift katlı integralde değişkenlerin değişimi 4.1. Bir noktanın eğrisel koordinatları kavramı uOv düzleminin D* bölgesinde, bu bölgede sürekli olduğunu düşüneceğimiz ve sürekli kısmi türevleri olan bir çift fonksiyon verilsin. Denklem (1) uyarınca, D* alanının her M*(a, v) noktası, xOy düzleminde belirli bir M(x, y) noktasına karşılık gelir ve dolayısıyla D* alanının noktaları, bir xOy düzlemindeki (x, y) noktalarından oluşan belirli bir D kümesi (Şekil 13). Bu durumda, fonksiyonların (1) D4 tanım kümesini D kümesine eşlediğini söylüyorlar. Farklı noktaların (u, v) farklı noktalara (x, y) karşılık geldiğini varsayalım. Bu, denklemlerin (1) u, v'ye göre benzersiz çözülebilirliğine eşdeğerdir: Bu durumda eşlemeye, D* alanının D alanına bire bir eşlenmesi denir. Böyle bir dönüşümle, herhangi bir D* alanında bulunan sürekli L* eğrisi, D bölgesinde bulunan sürekli bir L eğrisine girecektir. Eğer d(x) y) ve h(x, y) fonksiyonları da sürekli ise, o zaman herhangi bir sürekli çizgi LCD yardımıyla Dönüşümün (2) L* C D* sürekli çizgisi üzerinden geçecektir. Belirli bir çift Ш, değişkenlerin Vo değerleri ve D* bölgesinden v için, yalnızca M*(u) noktasının konumunu kesin olarak belirlemek mümkün değildir.<)> Vq) £)* bölgesindeki kendisi, ancak karşılık gelen M(xo, vo) noktasının D bölgesindeki konumu, xo = 4>(io, v0), 3/0 = o, vo). Bu, u, v sayılarını xOy düzlemindeki M bölgesinin D noktasının bazı yeni koordinatları olarak düşünmemize zemin hazırlar. Bunlara M noktasının eğrisel koordinatları denir. D alanındaki koordinatlardan birinin sabit kaldığı noktalar kümesine koordinat çizgisi denir. Formül (1)'de u = vq ayarlandığında koordinat çizgisinin parametrik denklemlerini elde ederiz.Burada parametrenin rolü u değişkeni tarafından oynanır. v koordinatına çeşitli (mümkün olan) sabit değerler vererek, xOy düzleminde bir koordinat çizgileri ailesi (v = const) elde ederiz. Benzer şekilde başka bir koordinat çizgisi ailesi elde ederiz (u = const). D* ve D bölgeleri arasında birebir örtüşme varsa aynı ailenin farklı koordinat çizgileri birbirini kesmez ve her aileden bir çizgi D bölgesinin herhangi bir noktasından geçer. xOp düzlemindeki eğrisel koordinat çizgilerinin ızgarası, uOv düzlemindeki dikdörtgen ızgaranın görüntüsüdür (bkz. Şekil 13). 4.2. Eğrisel koordinatlarda alan öğesi. Jacobian ve geometrik anlamı Uo*V düzlemindeki D* bölgesinde, kenarları 0*u ve O"v koordinat eksenlerine paralel ve kenar uzunlukları Ai ve Av olan küçük bir P*P?P$Pl dikdörtgenini seçelim. (kesinlik için, A ) sırasıyla (Şekil 14 a).Dikdörtgen alanı, D alanında eğrisel bir dörtgen *'e dönüşür (Şekil 146).Eğer P köşeleri koordinatlara sahipse, o zaman formüllere göre (1) ), karşılık gelen Pi köşeleri koordinatlara sahiptir), İki değişkenli bir fonksiyon için Taylor formülünü kullanarak ve kendimizi A ve Av'ye göre birinci dereceden/pc terimleriyle sınırlandırarak, a'nın köşeleri için aşağıdaki yaklaşık koordinat değerlerini elde ederiz. Fonksiyonların ve bunların tüm türevlerinin noktada hesaplandığı dörtgen. Noktaların koordinatları için bulunan ifadeler, P\PiPiPa dörtgeninin en küçüğüne kadar daha yüksek dereceli bir paralelkenar olduğunu göstermektedir.Bu, DS alanının DS alanı olduğu gerçeğinden kaynaklanmaktadır. dörtgen yaklaşık olarak vektör çarpımının uzunluğu cinsinden ifade edilebilir, Çift katlı integral kavramına yol açan problem Çift katlı integralin tanımı Çift katlı integralin temel özellikleri Düz bir bölgenin alanı Çift katlı integralin tekrarlanan bir Çift katlı integralde değişkenlerin değiştirilmesi Eğrisel koordinatlarda alan elemanı Jacobian ve geometrik anlamı Çift katlı integralde değişkenleri değiştirme formülü Kutupsal koordinatlarda çift katlı integral Belirleyici Videonun (7) ve (8) formüllerinden, Jacobian'ın mutlak değeri dönüşüm formülleri (1) kullanılarak D alanına haritalanırken D" bölgesinin (bu noktada (tx, v)) yerel gerilme katsayısı rolünü oynar. 4.3. Çift katlı integralde değişkenleri değiştirmek için formül Sürekli fonksiyonların D* alanının D üzerine bire bir eşlemesini yapmasına ve birinci dereceden sürekli kısmi türevlerine sahip olmasına izin verin. xOy düzlemindeki D bölgesinde sürekli bir fonksiyon verilsin. D bölgesindeki fonksiyonun her değeri, D" bölgesindeki r = fonksiyonunun eşit bir değerine karşılık gelir, burada. D* bölgesini bölelim kısmi bölgelere ayırın ve D bölgesinin karşılık gelen bir bölümünü oluşturun. İlgili kısmi bölgelerdeki (u, v) ve (x, y) noktaları seçin, böylece içlerindeki fonksiyonların değerleri çakışır ve bunun için integral toplamlar oluştururuz. D ve D* alanları üzerinde z = /(x, y) ve v) fonksiyonları.Fonksiyonların Jacobian'ını elde ederiz.D\ kısmi bölgelerinin en büyük çapı d* olarak limite eşitliğe (9) gidersek, sıfıra (haritanın (I) sürekliliğinden dolayı, D'deki kısmi bölgelerin d çaplarından en büyüğü sıfıra yönelecektir), J Koşulu Ф 0'ın yerel bire bir eşlemenin taşındığı koşul olduğu duruma sahip olacağız Teorem 4. Kartezyen koordinatlarda belirtilen çift katlı integrali eğrisel koordinatlarda çift katlı integrale dönüştürmek için, /(x, y) integrand fonksiyonundaki x ve y değişkenlerini sırasıyla alan boyunca değiştirmek gerekir. element dx dy - eğrisel koordinatlardaki ifadesi: Örnek. Hiperbol m ile sınırlanan bir şeklin alanını bulun.Belirtilen şeklin alanını bulmak, O bölgesi üzerindeki çift katlı integralin hesaplanmasına gelir.Yeni, eğrisel koordinatlar ve ve o'yu formüllerle tanıtalım Koşuldan denklemin, yani. Bu, uOv düzleminde bir dikdörtgen elde ettiğimiz anlamına gelir (Şekil 156) - verilen şekil D'den daha basit bir şekil. x ve y'yi (11)'den u ve t>'ye kadar olan ilişkilerden ifade edelim: Şekil 15 Sonra Çift katlı integral kutupsal koordinatlarda Çift katlı integralin hesaplanması genellikle x ve y dikdörtgen koordinatlarının aşağıdaki formüllere göre kutupsal koordinatlarla değiştirilmesiyle basitleştirilir. Kutupsal koordinatlardaki alan elemanı, Kartezyen koordinatlardaki integralden integrale geçiş için form ve formüle sahiptir. Kutupsal koordinatlar şu şekilde yazılabilir: Bu durumda (13) Kutupsal koordinatlardaki alan elemanı geometrik değerlendirmelerden elde edilebilir (bkz. Şekil 16). Şekildeki gölgeli alanın alanı A = pl. sektörler. sektörler Yüksek mertebeden sonsuz küçük miktarı bir kenara bırakarak, onu kutupsal koordinatlarda bir alan elemanı olarak elde edip alıyoruz. Dolayısıyla, Kartezyen koordinatlardaki bir çift katlı integrali kutupsal koordinatlardaki bir çift katlı integrale dönüştürmek için, integrandtaki a: ve y'yi sırasıyla p costp ve psini ile değiştirmeniz ve Kartezyen koordinatlardaki dx dy alan elemanını da ile değiştirmeniz gerekir. kutupsal koordinatlarda alan elemanı p dp dip. Şimdi çift katlı integrali kutupsal koordinatlarda hesaplamaya başlayalım. Dikdörtgen Kartezyen koordinatlarda olduğu gibi, kutupsal koordinatlardaki integralin hesaplanması, onu yinelenen bir integrale indirgeyerek gerçekleştirilir. Öncelikle O kutbunun belirli bir D bölgesinin dışında yer aldığı durumu ele alalım. D bölgesinin, kutuptan çıkan herhangi bir ışının (y koordinat çizgisinin sınırıyla en fazla iki noktada veya tüm bir bölüm boyunca kesişmesi) özelliğine sahip olmasına izin verin. (Şekil 17). Kutup açısının i uç değerlerinin dış entegrasyonun sınırları olduğuna dikkat edin. μ> = ışın, D bölgesinin konturunun A noktasından ve ışın B noktasından geçer. Aw B Noktaları D bölgesinin konturunu iki parçaya bölün: ACB ve AFB. Kutupsal denklemleri olsun ve) koşulu sağlayan tek değerli sürekli fonksiyonlardır. Fonksiyonlar iç entegrasyonun sınırlarıdır. Tekrarlanan integrallere geçerek aşağıdaki formülü elde ederiz: Özellikle D bölgesinin S alanı için F(p, r 1) elde ederiz. Şimdi O kutbu D bölgesinin içinde olsun. direğe göre yıldızdır, yani herhangi bir ışın tp = const bölgenin sınırıyla yalnızca bir noktada veya tüm bir bölüm boyunca kesişir (Şekil 18). Bölgenin sınırının kutupsal koordinatlardaki denklemi olsun. Şekil 18 Örnek: Bölgenin birinci çeyrekte yer alan birim çemberin dörtte biri olduğu integrali hesaplayın Kutupsal koordinatlara geçelim O zaman integralin alanı bir dikdörtgen olacaktır Dönüştürülen integral / kolayca hesaplanır: d Not: Eğer Jakoben D alanında sıfırdan farklı ise, o zaman bu alandaki her noktanın belirli bir komşuluğundaki haritalama bire birdir. Bununla birlikte, tüm alanın haritalanmasının bire bir olmaması da mümkündür. Fonksiyonların tanımladığı eşlemeyi ele alalım: Bu fonksiyonların Jacobian'ı eşittir ve dolayısıyla her yerde sıfırdan farklıdır. Ne olursa olsun, bu eşlemenin bire bir olmadığını anlıyoruz. Öte yandan, eğer bir haritalamanın Jacobian'ı bir noktada kaybolursa, o zaman yine de bu noktanın komşuluğundaki haritalama bire bir ortaya çıkabilir. Örneğin, işlevler tarafından tanımlanan bir eşleme için Jacobian sıfıra ve at'ye eşittir, ancak eşleme bire birdir. Ters eşleme işlevler tarafından belirlenir
1.1 Çift katlı integralin tanımı





1.2 Çift katlı integralin özellikleri
Çift katlı bir integralin özellikleri (ve bunların türetilmesi), tek bir belirli integralin karşılık gelen özelliklerine benzer.
1°. Toplanabilirlik. f(x, y) fonksiyonu bir D bölgesinde integrallenebilirse ve D bölgesi sıfır alanlı bir Г eğrisi ile ortak iç noktaları olmayan bağlantılı iki D1 ve D2 bölgesine bölünürse, f(x) fonksiyonu , y) D 1 ve D 2 alanlarından her birine entegre edilebilir ve
2°. Doğrusal özellik. Eğer f(x, y) ve g(x, y) fonksiyonları D bölgesinde integrallenebilirse, öyle mi? Ve? - herhangi bir gerçek sayı varsa, o zaman fonksiyon [? · f(x, y) + ?· g(x, y)] ayrıca D bölgesinde integrallenebilir ve
3°. Eğer f(x, y) ve g(x, y) fonksiyonları D bölgesinde integrallenebilirse, bu fonksiyonların çarpımı da D bölgesinde integrallenebilirdir.
4°. Eğer f(x, y) ve g(x, y) fonksiyonlarının her ikisi de D bölgesinde ve bu f(x, y) bölgesinin her yerinde integrallenebilirse? g(x, y), o halde
5°. Eğer f(x, y) fonksiyonu D bölgesinde integrallenebilirse, |f(x, y)| fonksiyonu D alanına entegre edilebilir ve
(Elbette |f(x, y)|'nin D'deki integrallenebilirliği, f(x, y)'nin D'deki integrallenebilirliği anlamına gelmez.)
6°. Ortalama değer teoremi. Hem f(x, y) hem de g(x, y) fonksiyonları bir D bölgesinde integrallenebilirse, g(x, y) fonksiyonu bu alandaki her yerde negatif değildir (pozitif değildir), M ve m D bölgesinde f( x, y) fonksiyonunun en üst ve en alt değeri varsa, o zaman m eşitsizliğini sağlayan bir sayı vardır? ? ? M ve formülün geçerli olduğu şekilde
Özellikle, f(x, y) fonksiyonu D'de sürekliyse ve D bölgesi bağlantılıysa, o zaman bu bölgede öyle bir (?, ?) noktası vardır ki? = f(?, ?) ve formül şu formu alır:
7°. Önemli geometrik özellik. D bölgesinin alanına eşit
Aşağıdan D bölgesiyle, yukarıdan sürekli ve negatif olmayan bir fonksiyonun grafiğiyle sınırlanan uzayda bir T cismi verilsin (Şekil 2.1), z=f (x, y), ki bu da şöyle tanımlanır: D bölgesi, yanlardan - kılavuzu D sınır bölgesi olan silindirik bir yüzeyle ve jeneratörler Oz eksenine paraleldir. Bu tip bir gövdeye silindirik gövde denir.
1.3 Çift katlı integralin geometrik yorumu





1.4 Bir dikdörtgen için çift katlı integral kavramı
R = ? dikdörtgeninin her yerinde keyfi bir f(x, y) fonksiyonu tanımlansın. (bkz. Şekil 1).

A segmentini bölelim mi? X? a = x 0 noktalarını kullanarak b'yi n kısmi parçaya ayırın< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.
Ox ve Oy eksenlerine paralel düz çizgiler kullanan bu bölme, R dikdörtgeninin n · p kısmi dikdörtgenler R kl = ?'ye bölünmesine karşılık gelir. (k = 1, 2, ..., n; l = 1, 2, ..., p). R dikdörtgeninin belirtilen bölümünü T sembolü ile belirtiyoruz. Bu bölümde ayrıca "dikdörtgen" terimi, kenarları koordinat eksenlerine paralel olan bir dikdörtgen olarak anlaşılacaktır.
Her kısmi dikdörtgen R kl üzerinde keyfi bir nokta seçiyoruz (? k, ? l). ?x k = x k - x k-1, ?y l = y l - y l-1'i koyarak, R kl dikdörtgeninin alanını?R kl ile gösteririz. Açıkçası, ?R kl = ?x k ?y l .
R dikdörtgeninin belirli bir T bölümü ile T bölümünün kısmi dikdörtgenleri üzerindeki belirli bir ara nokta seçimine (? k, ? l) karşılık gelen f(x, y) fonksiyonunun integral toplamı denir.
Köşegenine R kl dikdörtgeninin çapını diyeceğiz. Bir sembol? tüm kısmi dikdörtgenlerin çaplarından en büyüğünü R kl ile gösterelim.
I sayısına integral toplamlarının (1) limiti denir? Herhangi bir pozitif sayı için > 0? böyle pozitif bir sayı belirtebilir misiniz?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство
| ? - ben |< ?.
Bir f(x, y) fonksiyonuna, eğer bu fonksiyonun integral toplamlarının sonlu bir I limiti varsa, R dikdörtgeni üzerinde integrallenebilir Riemann fonksiyonu denir. > 0.
Belirtilen I limitine f(x, y) fonksiyonunun R dikdörtgeni üzerindeki çift katlı integrali denir ve aşağıdaki sembollerden biriyle gösterilir:
Yorum. Tek bir belirli integral için olduğu gibi, bir R dikdörtgeni üzerinde integrallenebilen herhangi bir f(x, y) fonksiyonunun bu dikdörtgen üzerinde sınırlı olduğu tespit edilmiştir.
Bu, yalnızca sınırlı f(x, y) fonksiyonlarının aşağıda dikkate alınmasına zemin hazırlar.
Çift katlı integral kavramına yol açan bir problem.
Parçaların fonksiyonunun tanımlı olduğunu varsayalım. ![]() ve tutarı yazın
ve tutarı yazın

buna integral denir.
A: Fonksiyonun ve seçimin belirli integrali (d.i.) altında ![]()
Tanım: 
Sayılara Riemann integrallenebilir denir.
T. varlığı: Şu şartla ki .
O.i.'nin tanımına uygun olarak. integralin türe, sınırlara bağlı olduğunu ve değişken tanımının sembolüne bağlı olmadığını, aksi takdirde ifade edildiğini not ediyoruz

Madde 17.1.1 ve 17.1.2'ye ve o.i. Eğrisel bir yamuğun alanı için formülü yazalım:  kuvvet işi
kuvvet işi ![]()
Açık : 
Çift katlı integral kavramı, integral toplamları.
Çift katlı bir integralin, yani integral toplamının bir limitinin varlığı açıktır, çünkü bu limit silindirik bir cismin hacmini verir. Ancak bu gerekçe kesin değildir. Daha kapsamlı derslerde bu ifade kesinlikle kanıtlanır ve çift katlı integralin varlığı teoremi olarak adlandırılır.

Varlık teoremi. Alanı a olan sınırlı bir kapalı bölgede sürekli olan herhangi bir fonksiyon için bir çift katlı integral vardır, yani her birinin bir a ile daralması koşuluyla, küçük alanların sayısında sınırsız bir artışla integral toplamlarının bir sınırı vardır. nokta. Bu sınır, bölgeyi parçalara ayırma yöntemine veya nokta seçimine bağlı değildir.
Aşağıda sadece integral alanında sürekli olan fonksiyonları ele alacağız.
Varlık teoreminden, örneğin a bölgesini düz kenarları koordinat eksenlerine paralel olan küçük dikdörtgenlere bölebileceğimiz sonucu çıkar (Şekil 230). burada. Daha sonra her küçük dikdörtgenin içinde bir nokta seçerek çift katlı integralin tanımına göre yazabiliriz.
Çift katlı integralin form toplamının limiti olarak elde edilebileceğini vurgulamak için notasyon yerine notasyonu da kullanıyoruz.
İfade Kartezyen koordinatlarda alan elemanı olarak adlandırılır ve kenarları koordinat eksenlerine paralel olan bir dikdörtgenin alanına eşittir.
İntegral toplamı derlenirken a alanının sınırına bitişik alanların dikdörtgen şekline sahip olmadığına dikkat edin. Ancak bu tür alanların sınırdaki alanlarla dikdörtgenlerle değiştirilmesinden kaynaklanan hatanın sıfıra ineceği kanıtlanabilir.
Çift katlı integrallerin özellikleri
Çift katlı bir integralin özellikleri (ve bunların türetilmesi), tek bir belirli integralin karşılık gelen özelliklerine benzer.
1°. toplanabilirlik. Eğer fonksiyon F(X, sen) etki alanında entegre edilebilir D ve eğer alan D bir eğri kullanma G sıfır alanı ortak iç noktaları olmayan iki bağlantılı bölgeye bölünmüştür D 1 ve D 2, ardından fonksiyon F(X, sen) her bir alana entegre edilebilir D 1 ve D 2 ve
2°. Doğrusal özellik. Eğer işlevler F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, A α Ve β - herhangi bir gerçek sayı, ardından fonksiyon [ α · F(X, sen) + β · G(X, sen)] ayrıca etki alanında entegre edilebilir D, Ve
![]()
![]()
3°. Eğer işlevler F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, o zaman bu fonksiyonların çarpımı şu şekilde integrallenebilir: D.
4°. Eğer işlevler F(X, sen) Ve G(X, sen) her ikisi de etki alanıyla entegre edilebilir D ve bu bölgenin her yerinde F(X, sen) ≤ G(X, sen), O
5°. Eğer fonksiyon F(X, sen) etki alanında entegre edilebilir D, ardından işlev | F(X, sen)| alanlara entegre edilebilir D, Ve
(Elbette entegre edilebilirlikten | F(X, sen)| V D entegre edilebilirlik takip etmiyor F(X, sen)V D.)
6°. Ortalama değer teoremi. Her iki işlev de varsa F(X, sen) Ve G(X, sen) alan adlarına entegre edilebilir D, işlev G(X, sen) bu bölgenin her yerinde negatif değildir (pozitif değildir), M Ve M- fonksiyonun tam üst ve tam alt sınırları F(X, sen) bölgede D, o zaman bir sayı var μ eşitsizliğin sağlanması M ≤ μ ≤ M ve formülün geçerli olduğu şekilde
Özellikle, eğer fonksiyon F(X, sen) süreklidir D ve bölge D tutarlı, o zaman bu bölgede böyle bir nokta var ( ξ , η ), Ne μ = F(ξ , η ) ve formül (11) şu formu alır
Olarak belirtilen iki değişkenli bir fonksiyon için z = F(X, sen) .
Çift katlı integral şu şekilde yazılır:
Burada D– çift katlı integralin hesaplanması görevinde ifadeleri (eşitlikler) verilen, çizgilerle sınırlanmış düz bir şekil. Sol ve sağ, soldaki değişkenin olduğu eşitliklerdir X, ve üstü ve altı – soldaki değişkenin olduğu eşitliklere göre sen. Burası çift katlı integral hesaplama tekniğinin anlaşılması için en önemli yerlerden biri olmaya devam ediyor.
Çift katlı integrali hesaplayın - belirtilen şeklin alanına eşit bir sayı bulmak anlamına gelir D .
Biz dokunana kadar çift katlı integral tanımları ve bunu hesaplamayı öğreneceğiz. Çift katlı integralin ne olduğunu anlamak, onu hesaplamak için birkaç problem çözdüğünüzde daha kolaydır; dolayısıyla çift katlı integralin tanımını bu dersin sonunda bulacaksınız. Biraz ileriye baktığımızda, çift katlı integralin tanımının da söz konusu şekil ile ilgili olduğunu söyleyebiliriz. D .
Şekil ise D bir dikdörtgendir ve onu sınırlayan tüm çizgiler düz çizgilerdir. Şekil ise D- eğriseldir, daha sonra solda ve sağda düz çizgilerle ve üstünde ve altında görevde verilen eşitliklerle verilen kavisli çizgilerle sınırlıdır. Bir figürün olduğu durumlar da vardır. D- bir üçgen, ancak bu gibi durumlarda daha fazlası biraz daha ileride.
Bu nedenle çift katlı integrali hesaplamak için şekli çevreleyen çizgileri sıralamak gerekir. D Kesin bir adı olan entegrasyon bölgesi. Sol ve sağ, üst ve alt olarak sıralayın. Bu, aşağıdaki durumlarda gerekli olacaktır: bir çift katlı integralin yinelenen bir integrale indirgenmesi – çift katlı integralin hesaplanması yöntemi.
Dikdörtgen alan durumu:

Eğri bir bölge durumu:

Ve bu zaten, entegrasyonun üst ve alt sınırlarının verildiği bilinen belirli integrallerin bir çözümüdür. Bir şekli sınırlayan çizgileri tanımlayan ifadeler D, halihazırda yaklaşmakta olduğumuz olağan belirli integrallerin integral limitleri olacaktır.
Çift katlı bir integralin tekrarlanan bir integrale indirgenmesi
Dikdörtgen bölge durumu
Böyle bir fonksiyonun çift katlı integrali olsun
İle bu çift katlı integrali değerlendirin , onu yinelenen bir integrale indirgememiz gerekiyor, bu da şu forma sahip:
![]() .
.
Önce iç (sağ) belirli integrali, ardından dış (sol) belirli integrali hesaplamanız gerekir.
Rolleri değiştirebilirsiniz X Ve sen
![]() .
.
Örnek 1.Çift katlı integrali hesaplayın

Y'yi bir sabit olarak kabul ederek iç (sağ) integrali hesaplıyoruz. Anladık.
 .
.

Örnek 2.Çift katlı integrali hesaplayın
![]() ,
,
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
Çizimde entegrasyon bölgesini oluşturuyoruz:


Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz:
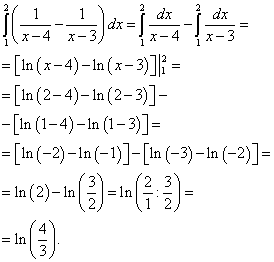
Sonuç bu çift katlı integralin çözümü olacaktır.
Çift katlı integrali kendiniz hesaplayın ve sonra çözüme bakın
Kavisli veya üçgen bölge durumu
Bize yine iki değişkenli bir fonksiyon verilsin F(X, sen) ve kısıtlamalar D: zaten biraz farklı bir türde:
Bu giriş, şeklin anlamına gelir D doğrusal bir bölgede olduğu gibi sol ve sağ sınırlıdır - düz çizgiler X = A Ve X = B, ancak altında ve üstünde denklemler tarafından verilen eğriler vardır ve . Başka bir deyişle ve fonksiyonlardır.
Böyle bir fonksiyonun çift katlı integrali olsun
Bu çift katlı integrali değerlendirmek için onu yinelenen bir integrale indirgememiz gerekir;
 .
.
İşte entegrasyonun sınırları A Ve B- sayılar ve ve - işlevler. Üçgensel bir bölge durumunda fonksiyonlardan biri düz bir çizginin denklemidir. Bu durum Örnek 3'te tartışılacaktır.
Doğrusal bir bölgede olduğu gibi, önce sağdaki belirli integrali, ardından soldaki belirli integrali hesaplamanız gerekir.
Aynı şekilde rolleri değiştirebilirsiniz X Ve sen. O zaman tekrarlanan integral şu şekle sahip olacaktır:
 .
.
Böyle tekrarlanan bir integral tamamen aynı şekilde çözülmelidir: önce - iç (sağ) integral, sonra - dış (sol) integral.
Örnek 5.Çift katlı integrali hesaplayın
![]() ,
,
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
![]() .
.
Çizimde entegrasyon bölgesini oluşturuyoruz ve bunun üçgen olduğunu görüyoruz:

X'in bir sabit olduğunu düşünerek iç (sağ) integrali hesaplıyoruz. Anladık.

Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz. Öncelikle bu integrali integrallerin toplamı olarak sunuyoruz:
![]() .
.
İlk terimi hesaplıyoruz:

İkinci terimi hesaplıyoruz:

Üçüncü terimi hesaplıyoruz:

Bu çift katlı integralin çözümü olacak toplamı elde ederiz:
![]() .
.
Örnek 6.Çift katlı integrali hesaplayın
Çözüm. Bu çift katlı integrali yinelenen bir integrale indirgeyelim
Çizimde entegrasyon bölgesini oluşturuyoruz:

X'in bir sabit olduğunu düşünerek iç (sağ) integrali hesaplıyoruz. Anladık.
 .
.
Şimdi az önce hesaplanan iç kısmın (sağ) dış (sol) integralini hesaplıyoruz:

Sonuç bu çift katlı integralin çözümü olacaktır.
X-doğru ve yanlış sen-doğru ve yanlış entegrasyon alanları
Bir çift katlı integralin integral alanı öyle çizgilerle sınırlıdır ki, integral alanını parçalara bölmek ve karşılık gelen her tekrarlanan integrali ayrı ayrı çözmek gerekli hale gelir. Bunlar aşağıdaki durumlarda geçerlidir:
1) entegrasyon alanı, alt veya üst (sol veya sağ) sınır şeklinde iki veya daha fazla düz veya kavisli çizgiye sahip bir şekildir;
2) İntegrasyon bölgesi, sınırları çizgilerin ikiden fazla noktada kesiştiği bir şekildir.
Yukarıdakilerin entegrasyon alanının sol veya sağ sınırı için geçerli olması durumunda, yani çizgilerle ifade edilen kısıtlamalar X, daha sonra entegrasyon alanı denir X-yanlış. Eğer çizgi sen = sen0 karşılık gelen sınırla yalnızca bir noktada kesişir ve sınır yalnızca bir düz çizgi veya eğri ise, o zaman entegrasyon alanı denir. X-doğru
Benzer şekilde, çizgilerle tanımlanan sınır şu şekilde ifade edilirse: sen, dümdüz X = X0 birden fazla noktada kesişiyorsa ya da sınır birden fazla düz çizgi ya da eğriden oluşuyorsa integralin tanım bölgesi denir. sen-yanlış. Şimdi işaretleri göster sen- muhtemelen doğru alan oldukça basittir.
Şu ana kadar örneklere baktık X-yanlış ve sen-doğru entegrasyon alanları. Şimdi doğruluk koşulunun ihlal edildiği durumları düşünün.
Örnek 7.İntegral alanı çizgilerle sınırlı olan bir çift katlı integrali hesaplayın sen = X , xy = 1 , sen = 2 .

Çözüm. Entegrasyon alanı sen-yanlış, çünkü alt sınırı tek bir çizgiyle belirtilemez sen = sen(X) . Yukarıdaki şekilde görüldüğü gibi alt sınır aşağıdakilerden oluşur: sen = X(koyu bordo) ve xy= 1 (yeşil). Bu nedenle doğrudan X= 1 (siyah), entegrasyon alanını iki parçaya bölebiliriz - ve .
Bu çift katlı integral şu şekilde hesaplanır:

Entegrasyon sırasını değiştirme
Yukarıda belirtildiği gibi, çift katlı integrali yinelenen bir integrale indirgedikten sonra değişkenleri değiştirebilirsiniz. X Ve sen rolleri değiştirir veya başka bir deyişle entegrasyonun sırasını değiştirir.
Entegrasyon sırasındaki değişiklik mecazi olarak O'Henry'nin şu sözleriyle açıklanabilir: "Bir orman sakini - bir hayvan - kafese girdiğinde bu şekilde davranır ve kafesteki bir sakin - bir insan - bu şekilde davranır - şüphe ormanında kaybolduğunda öyle davranır." O'Henry'ye göre sonuç aynı ve aynı: "Chalmers mektubu bin küçük parçaya böldü ve pahalı halısını yırtmaya başladı, geri dönüp yürüdü ve bunun üzerine ileri." ( O.Henry. Madison Meydanı'ndan Şehrazat.)
O zaman değişkenin sol integrali X ve doğru olanı - tarafından sen, entegrasyon sırasını değiştirdikten sonra her şey tam tersi olacaktır. Daha sonra "yeni" oyun için entegrasyon sınırları "eski" X'ten "ödünç alınmalı" ve "yeni" X için entegrasyon sınırları şu şekilde elde edilmelidir: ters fonksiyon y'nin limitini belirleyen denklemi x için çözüyoruz.
Örnek 8.
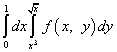 .
.
Çözüm. İntegral sırası değiştirildikten sonra, y üzerindeki integral solak, x üzerindeki integral ise sağ yönlü olacaktır. "Yeni" oyun için entegrasyon limitlerini "eski" X'ten ödünç alacağız, yani alt limit sıfıra, üst limit ise bire eşittir. “Eski” oyun için entegrasyon sınırları denklemler ve ile verilmiştir. Bu denklemleri x için çözdükten sonra x için yeni entegrasyon limitleri elde ederiz:
(alt) ve (üst).
Böylece integralin sırası değiştirildikten sonra tekrarlanan integral şu şekilde yazılacaktır:
 .
.
Çift katlı bir integralde integralin sırası değiştirildikten sonra, integralin alanı genellikle şuna dönüşür: sen-yanlış veya X-yanlış (önceki paragrafa bakınız). Daha sonra entegrasyon alanını parçalara ayırmanız ve karşılık gelen her bir yinelenen integrali ayrı ayrı çözmeniz gerekir.
İntegral alanını parçalara ayırmak birçok öğrenci için bazı zorluklar oluşturduğundan, kendimizi bir önceki paragrafta verilen örnekle sınırlamayacağız, birkaç örneğe daha bakacağız.
Örnek 9. Yinelenen integral için entegrasyon sırasını değiştirin
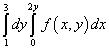 .
.
Çözüm. Yani bu yinelenen integralin integral alanı düz çizgilerle sınırlıdır sen = 1 , sen = 3 , X = 0 , X = 2sen .
Farklı bir düzende entegrasyon yapıldığında bölgenin alt sınırı iki düz çizgiden oluşur: AB Ve M.Ö. denklemlerle verilen sen= 1 ve sen = X/2, aşağıdaki şekilde görüldüğü gibi.

Bu belirsizlikten kurtulmanın yolu entegrasyon alanını iki parçaya ayırmaktır. Entegrasyon alanının bölümü düz bir çizgi olacaktır BM. Ters fonksiyonu bularak yeni entegrasyon limitlerini hesaplıyoruz. Bu çözüme göre integralin sırası değiştirildikten sonra tekrarlanan integral iki integralin toplamına eşit olacaktır:

Doğal olarak, bu örnekte verilen tekrarlanan integrale indirgenen çift katlı integralin çözümü de aynı olacaktır.
Örnek 10. Yinelenen integral için entegrasyon sırasını değiştirin
 .
.
Çözüm. Dolayısıyla yinelenen integralin integral alanı düz çizgilerle sınırlıdır X = 0 , X= 2 ve eğriler ve .
Aşağıdaki şekilde görüldüğü gibi eksene paralel bir doğru 0x, entegrasyon alanının alt sınırını ikiden fazla noktada kesecektir.

Bu nedenle entegrasyon alanını şekilde siyahla çizilen düz çizgilerle üç parçaya bölüyoruz. Ters fonksiyonu bularak yeni entegrasyon limitlerini hesaplıyoruz. Üç yeni entegrasyon alanının sınırları aşağıdaki gibi olacaktır.


Bu çözüme göre integralin sırası değiştirildikten sonra tekrarlanan integral üç integralin toplamına eşit olacaktır:

Üç integralin aynı toplamı, bu örnekte verilen tekrarlanan integrale indirgenen çift katlı integrale eşit olacaktır.
Ancak yine de mücbir sebepler, öğrencilerin zaten bir önceki adımda olmalarına engel oluyor ve entegrasyonun sınırlarını belirliyor. Kaygı ve kafa karışıklığının bir temeli yok: İntegral bölgesini parçalara bölmek için genellikle çizime yakından bakmak ve tekrarlanan integrali (integral tablosu) çözmek yeterliyse, o zaman limitleri belirleme konusunda biraz eğitim deneyimine ihtiyaç vardır. entegrasyon. Yalnızca entegrasyonun sınırlarını belirlemeye odaklanacağımız ve - neredeyse otomatik olarak - bölgeyi bölümlemeye ve çözümün kendisini atlamaya odaklanacağımız bir örnek üzerinden gidelim.
Örnek 11.İntegral tanım kümesi ise çift katlı integralin integral limitlerini bulun Dşu şekilde verilmiştir:
sen - 2X ≤ 0;
2 yıl - X ≥ 0;
xy ≤ 2.
Çözüm. Açıkça (üzerinden X Ve sen"safsızlıklar olmadan") entegrasyon bölgesini sınırlayan çizgiler belirtilmemiştir. X için çoğunlukla i ile ifade edilen üst ve alt sınırlara bir noktada dokunan düz çizgiler olduklarından, o zaman tam olarak bu yol boyunca ilerleyeceğiz. Üstelik entegrasyon sırasını değiştirdiğimizde aynı alana sahip bir entegrasyon bölgesi elde ediyoruz. Oyundaki eşitsizlikleri çözelim ve şunu elde edelim:
sen ≤ 2X;
sen ≥ X/2;
sen ≤ 2/X.
Ortaya çıkan çizgileri çizime göre oluşturuyoruz. X üzerinden integralin sınırları aslında çizgilerdir X= 0 ve X= 2 . Ancak entegrasyon alanı ortaya çıktı sen-yanlış, çünkü üst sınırı tek satırla belirtilemez sen = sen(X) .
Okumak faydalı olabilir:
- Ücretlerin ödenmemesi nedeniyle işten çıkarma başvurusu;
- Paragrafta gönüllü işten çıkarma hakkında söylenenler;
- Kayıp makbuz nasıl kurtarılır Sberbank makbuzunu kaybettim, kurtarılabilir mi?;
- Vergi indirimine başvurmak için kişisel hesap numarasını nereden alabilirim?;
- Mal ithalatı ve dolaylı vergilerin ödenmesi için başvuru listesini doldurma prosedürü Belarus'ta dolaylı vergilerin ödenmesini kontrol edin;
- Bir kuruluşun hanını ada göre arayın;
- Muhasebe derslerinde uzaktan eğitim;
- Ölçme büyüklükleri Fizikte ölçülenler;