ویژگی های اساسی انتگرال دوگانه وظیفه تعریف انتگرال دوگانه از ویژگی های اصلی انتگرال دوگانه مفاهیم و تعاریف اساسی انتگرال دوگانه

ویژگی های اساسی انتگرال دوگانه

خواص انتگرال مضاعف (و اشتقاق آنها) مشابه خواص متناظر انتگرال معین منفرد است.

1 درجه. افزودنی. اگر تابع f(ایکس, y) در دامنه قابل ادغام است Dو اگر منطقه Dبا استفاده از یک منحنی جیمنطقه صفر به دو منطقه متصل بدون نقاط داخلی مشترک تقسیم می شود D 1 و D 2، سپس تابع f(ایکس, y) در هر یک از دامنه ها قابل ادغام است D 1 و D 2، و

2 درجه. ویژگی خطی. اگر توابع f(ایکس, y) و g(ایکس, y) در دامنه قابل ادغام هستند D، آ α و β هر عدد واقعی است، سپس تابع [ α · f(ایکس, y) + β · g(ایکس, y)] نیز در دامنه قابل ادغام است D، و

3 درجه. اگر توابع f(ایکس, y) و g(ایکس, y) در دامنه قابل ادغام هستند D، سپس محصول این توابع نیز قابل ادغام است D.

4 درجه. اگر توابع f(ایکس, y) و g(ایکس, y) هر دو در دامنه قابل ادغام هستند Dو در همه جای این منطقه f(ایکس, y) ≤ g(ایکس, y) آن

5 درجه. اگر تابع f(ایکس, y) در دامنه قابل ادغام است D، سپس تابع | f(ایکس, y)| قابل ادغام در منطقه D، و

(البته از یکپارچگی | f(ایکس, y)| V Dیکپارچگی به دنبال ندارد f(ایکس, y) V D.)

6 درجه. قضیه مقدار میانگین. اگر هر دو عملکرد دارند f(ایکس, y) و g(ایکس, y) در دامنه قابل ادغام هستند D، تابع g(ایکس, y) در همه جای این منطقه غیر منفی (غیر مثبت) است، مو متر- مرزهای دقیق بالا و پایین تابع f(ایکس, y) در منطقه D، سپس یک عدد وجود دارد μ ، ارضای نابرابری متر ≤ μ ≤ مو به گونه ای که فرمول

مسئله منجر به مفهوم یک انتگرال دوگانه تعریف یک انتگرال دوگانه ویژگی های اساسی یک منطقه انتگرال دوگانه یک منطقه مسطح کاهش یک انتگرال دوگانه به یک تکرار شده تغییر متغیرها در یک عنصر مساحت انتگرال دوگانه در مختصات منحنی ژاکوبین و معنی هندسی آن تغییر فرمول متغیرها در یک انتگرال دوگانه انتگرال دوگانه در مختصات قطبی

مسئله ای که منجر به مفهوم انتگرال دوگانه می شود. تعریف انتگرال دوگانه با حل یک مسئله خاص در محاسبه حجم یک جسم استوانه ای به مفهوم انتگرال دوگانه می رسیم. یک جسم استوانه ای جسمی است که توسط صفحه xOy، مقداری سطح و یک سطح استوانه ای محدود شده است که مولدهای آن با محور موازی هستند (شکل 1 را ببینید). مساحت D تغییر متغیرهای x و y را قاعده جسم استوانه ای می نامند. هنگام تعیین حجم بدن، از دو اصل عمل می کنیم: !) اگر جسم به قطعات تقسیم شود، حجم آن برابر است با مجموع حجم های همه اجزا (خاصیت افزودنی). 2) حجم یک استوانه مستقیم محدود به صفحه z = const، موازی با صفحه xOy، برابر است با مساحت پایه ضرب در ارتفاع. در ادامه، فرض می‌کنیم که دامنه D متصل (شامل یک قطعه)، مربع (یعنی دارای یک مساحت) و محدود است (یعنی در داخل دایره‌ای به مرکزیت مبدا قرار دارد). فرض کنید یک تابع پیوسته از نقطه P(x, y) در دامنه در همه جای حوزه Z> باشد، یعنی سطح استوانه‌ای مورد بررسی کاملاً بالای صفحه xOy باشد. حجم جسم استوانه‌ای را با V نشان می‌دهیم. اجازه دهید ناحیه D - پایه بدنه استوانه‌ای - را به تعداد معینی n از مناطق مربع غیرمتقاطع با شکل دلخواه تقسیم کنیم. ما آنها را مناطق جزئی می نامیم. با شماره گذاری مناطق جزئی به ترتیب، مناطق - از طریق. ما قطر یک منطقه جزئی را Dk مقدار می نامیم مشکل منجر به مفهوم یک انتگرال دوگانه تعریف یک انتگرال دوگانه ویژگی های اساسی یک منطقه انتگرال دوگانه یک منطقه مسطح کاهش یک انتگرال دوگانه به یک تکرار شده تغییر متغیرها در یک عنصر انتگرال دوگانه مساحت در مختصات منحنی خطی ژاکوبین و معنای هندسی آن تغییر فرمول متغیرها در یک انتگرال دوگانه انتگرال دوگانه در مختصات قطبی که در آن نماد p(P; Q) نشان دهنده فاصله بین نقاط P و Q است. اجازه دهید d نشان دهنده بزرگترین قطر مناطق جزئی Dk (k = 1,2,...,n). اجازه دهید یک سطح استوانه ای را از طریق مرز هر ناحیه جزئی با ژنراتورهای موازی با محور Oz ترسیم کنیم. در نتیجه بدنه استوانه ای به n جسم استوانه ای جزئی تقسیم می شود. اجازه دهید بدنه جزئی k-امین را با یک استوانه مستقیم با همان پایه و ارتفاعی برابر با کاربرد نقطه ای از سطح جایگزین شده جایگزین کنیم (شکل 2). حجم چنین استوانه ای جایی است که نقطه مساحت منطقه Dk است. با انجام ساختارهای توصیف شده برای هر جسم استوانه ای جزئی، یک بدنه n مرحله ای به دست می آوریم که حجم آن (o) به طور مستقیم واضح است که Vn حجم V مورد نظر را با دقت بیشتری بیان می کند، ابعاد مناطق جزئی Dk کوچکتر است. . ما حجم V جسم استوانه‌ای را برابر با حدی می‌پذیریم که حجم (1) بدنه n مرحله‌ای به آن سمت می‌رود، زیرا بزرگترین قطر d از نواحی جزئی Dk به صفر میل می‌کند. طبیعتاً محدودیت نباید به نوع تقسیم دامنه D به دامنه های جزئی Dk و انتخاب نقاط Pk در حوزه های جزئی بستگی داشته باشد. فرض کنید f(x,y) یک تابع دلخواه باشد که در دامنه D تعریف شده است. مجموع n (1) مجموع انتگرال تابع f(x)y) روی دامنه D مربوط به یک پارتیشن معین از این دامنه در نامیده می شود. n دامنه جزئی و یک انتخاب معین از نقاط ®*,!/*) در دامنه های جزئی Dk. تعریف. اگر برای d - * 0 حدی از مجموع انتگرال n وجود داشته باشد که به روش تقسیم دامنه D به حوزه های جزئی و یا به انتخاب نقاط Pk در حوزه های جزئی بستگی ندارد، آن را انتگرال دوگانه می نامند. تابع f(P) (یا f(x, y )) روی دامنه D و با نماد OR نشان داده می شود بنابراین، (2) خود تابع f(x, y) در دامنه D انتگرال پذیر نامیده می شود (f( P) انتگرال است، f(P) dS انتگرال است، dS دیفرانسیل (یا عنصر) ناحیه است، ناحیه D ناحیه ادغام است؛ نقطه P (®، y) یکپارچه سازی ظریف متغیر است) . ,.. با بازگشت به جسم استوانه ای نتیجه می گیریم: حجم جسم استوانه ای محدود به صفحه xOy، سطح و سطح استوانه ای با ژنراتورهای موازی با محور Oz برابر با انتگرال دوگانه تابع f(x است. ، y) بر روی ناحیه D که قاعده جسم استوانه ای است. / یا در اینجا dx dy عنصر مساحت در مختصات دکارتی است. این معنای هندسی انتگرال دوگانه یک تابع غیر منفی است. اگر حجم اگر در ناحیه D تابع f (P) هر دو مقدار مثبت و منفی را بگیرد، انتگرال نشان‌دهنده مجموع جبری حجم‌های آن قسمت‌هایی از بدن است که بالای صفحه xOy قرار دارند. علامت «+»)، و آن قسمت‌هایی از بدن که در زیر صفحه xOy قرار دارند (با علامت «-» گرفته شده‌اند). انواع مسائل منجر به جمع آوری مجموع شکل (1) برای تابعی از دو متغیر مستقل و عبور بعدی به حد می شود و نه تنها مشکل حجم یک جسم استوانه ای. اجازه دهید شرایط کافی برای یکپارچگی را فرموله کنیم. قضیه 1. هر تابع y) پیوسته در یک دامنه بسته محدود D در این حوزه قابل ادغام است. الزام برای تداوم انتگرال اغلب بسیار محدود کننده است. برای کاربردها، قضیه زیر مهم است که وجود یک انتگرال مضاعف را برای کلاس خاصی از توابع ناپیوسته تضمین می کند. اگر بتوان آن را در یک شکل چند ضلعی با مساحت دلخواه کوچک محصور کرد، خواهیم گفت که مجموعه ای از نقاط در یک صفحه دارای مساحت صفر است. قضیه 2. اگر یک تابع f(x, y) در یک دامنه محدود بسته D محدود شده باشد و در همه جای D پیوسته باشد، به جز مجموعه ای از نقاط مساحت صفر، آنگاه این تابع در دامنه D قابل ادغام است. §2. ویژگی های اساسی انتگرال های دو انتگرال دوگانه دارای تعدادی ویژگی مشابه با ویژگی های انتگرال معین برای توابع یک متغیر مستقل هستند. 2.1. ویژگی خطی اگر توابع a) در حوزه D قابل انتگرال باشند و a و p هر اعداد حقیقی باشند، تابع af) نیز در دامنه D قابل انتگرال است و o) 2.2. ادغام نابرابری ها اگر توابع در دامنه D و همه جای این دامنه قابل ادغام باشند، (2)، یعنی نابرابری ها را می توان ادغام کرد. به طور خاص، با ادغام نابرابری های آشکار، مساحت یک ناحیه مسطح را به دست می آوریم. مساحت ناحیه مسطح D برابر است با انتگرال دوگانه روی این ناحیه از تابعی که به طور یکسان برابر با یک است. در واقع، مجموع انتگرال برای تابع /(P) = 1 در دامنه D شکل دارد و برای هر تقسیم دامنه D به دامنه های جزئی Dt، برابر با مساحت آن S است. اما پس از آن حد این مجموع، i.e. انتگرال مضاعف برابر است با مساحت S حوزه های D: یا، که یکسان است، (3) 2.4. تخمین انتگرال اجازه دهید تابع /(P) در یک ناحیه بسته محدود D پیوسته باشد، اجازه دهید M و mn بزرگترین و کوچکترین مقادیر /(P) در منطقه D باشند و 5 مساحت آن باشد. سپس (4) 2.5. افزودنی: اگر تابع /(P) در دامنه D قابل ادغام باشد و دامنه Z) به دو دامنه D\ و Di بدون نقاط داخلی مشترک تقسیم شود، /(P) در هر یک از دامنه های D\ و Di قابل ادغام است. و (5) 2.6. قضیه روی مقدار میانگین قضیه 3 (درباره مقدار میانگین). اگر تابع /(P) در یک منطقه محدود بسته D پیوسته باشد، حداقل یک نقطه Pc از ناحیه D وجود دارد که فرمول u معتبر است، جایی که S مساحت ناحیه D دامنه D است. سپس در D بزرگترین مقدار خود را M و کوچکترین مقدار خود را به خود اختصاص می دهد. با خاصیت 4 در تخمین انتگرال، P) در دامنه D، در نقطه ای Pc G D مقداری برابر با این عدد می گیرد، از آنجا که S مقدار f(Pc) که با فرمول (7) تعیین می شود، مقدار میانگین تابع f(P) در دامنه D نامیده می شود. مقدار اگر در ناحیه D تابع /(P) ^ O باشد، فرمول (6) به این معنی است که یک استوانه مستقیم با پایه D (که مساحت آن 5 است) و ارتفاع H = /(Pc) وجود دارد که حجم آن برابر با حجم یک جسم استوانه ای است (شکل . 3). § 3. تقلیل انتگرال مضاعف به انتگرال تکراری یکی از روش های موثر برای محاسبه انتگرال مضاعف، کاهش آن به انتگرال تکرار شده است. 3.1. حالت یک مستطیل، ناحیه D یک مستطیل بسته Π با اضلاع موازی با محورهای مختصات باشد. فرض کنید تابع f(x,y) در مستطیل P پیوسته باشد. انتگرال دوگانه را می توان به عنوان حجم (جبری) یک جسم استوانه ای با پایه P محدود به یک سطح تفسیر کرد. جسم استوانه ای مربوطه را در نظر بگیرید. بیایید صفحه ای عمود بر محور Oy رسم کنیم (شکل 4). این صفحه بدنه استوانه ای را در امتداد یک ذوزنقه منحنی، که از بالا با یک خط مسطح z محدود شده است، برش می دهد، که با معادلات توصیف می شود. آرگومان دوم انتگرال - به عنوان یک ثابت در نظر گرفته می شود. مقدار انتگرال (1) به انتخاب مقدار y0 بستگی دارد. ما (2) را تنظیم می کنیم عبارت (2) سطح مقطع اجسام استوانه ای را به عنوان تابعی از y می دهد. بنابراین، حجم یک جسم استوانه ای را می توان با فرمول محاسبه کرد، از طرف دیگر، این حجم با انتگرال دوگانه تابع /(x,y) بر روی مستطیل P بیان می شود. بنابراین، S(y) را با آن جایگزین می کنیم. در بیان (2)، مسئله ای را به دست می آوریم که منجر به مفهوم یک انتگرال دوگانه می شود. انتگرال عنصر مساحت در مختصات منحنی ژاکوبین و معنای هندسی آن تغییر فرمول متغیرها در یک انتگرال دوگانه انتگرال دوگانه در مختصات قطبی آخرین رابطه معمولاً به صورت زیر نوشته می شود. صفحات x = x0. این منجر به فرمول (4) می‌شود. هر یک از عبارات سمت راست فرمول‌های (3) و (4) شامل دو عملیات متوالی ادغام معمولی تابع f(x,y) است. آنها را انتگرال های تکراری تابع f(x,y) روی دامنه Π می نامند. اگر f(x,y) در مستطیل بسته Π پیوسته باشد، عبور به انتگرال های تکرار شده همیشه امکان پذیر است، و (5) یعنی، مقادیر انتگرال های تکرار شده تابع پیوسته /(x,y) به ترتیب ادغام بستگی ندارد. مثال 1. انتگرال دوگانه یک تابع را در مساحتی که داریم پیدا کنید (شکل 5 را ببینید): 3.2. مورد یک دامنه دلخواه اکنون فرض کنیم که حوزه ادغام یک دامنه بسته مربعی محدود شده دلخواه D در صفحه xOy است که شرایط زیر را برآورده می کند: هر خط مستقیم موازی با محور Oy، مرز دامنه D را بیش از حد قطع نمی کند. دو نقطه یا در امتداد یک قطعه کامل (شکل . 6 الف). همانطور که در شکل نشان داده شده است، ناحیه D را در داخل مستطیل محصور می کنیم. 66. پاره [a, 6] یک برآمدگی متعامد از ناحیه D بر روی محور Oxy است و قطعه [c, dj یک طرح متعامد از ناحیه D بر روی محور Oy است. با نقاط A و C، مرز منطقه D به دو منحنی ABC و AEC تقسیم می شود. هر یک از این منحنی ها با یک خط مستقیم دلخواه موازی با محور Oy در بیش از یک نقطه تلاقی می کنند. بنابراین، معادلات آنها را می‌توان به شکل مجاز برای y نوشت: فرض کنید f(x,y) تابعی پیوسته در حوزه D باشد. اجازه دهید جسم استوانه‌ای مورد نظر را با یک صفحه برش دهیم. در بخش، یک PQMN ذوزنقه منحنی خطی به دست می‌آوریم (شکل 7)، مساحتی که با یک انتگرال معمولی از تابع / (x, y) بیان می‌شود که به عنوان تابعی از یک متغیر y در نظر گرفته می‌شود. در این حالت، متغیر y از ترتیب نقطه P به ترتیب نقطه Q تغییر می کند \ نقطه P "ورودی" *!-ka خط x = const (در صفحه) به منطقه است - نقطه "خروج" آن از این منطقه است. از آنجایی که معادله ای برای منحنی ABC و برای منحنی وجود دارد، وقتی x گرفته می شود، این مختصات به ترتیب برابر هستند. بنابراین، انتگرال به ما بیانی برای مساحت یک بخش مسطح از یک جسم استوانه ای به عنوان تابعی از موقعیت صفحه سکونت x = const به ما می دهد. حجم کل بدن برابر با انتگرال این عبارت بر w در بازه تغییر خواهد بود. بنابراین، به طور خاص، برای ناحیه S از ناحیه D به دست می آوریم. اجازه دهید فرض کنیم که هر خط مرز منطقه D را در بیش از دو نقطه P و Q قطع می کند که ابسیساهای آنها به ترتیب برابر هستند (یا در امتداد). یک بخش کامل) (شکل 8). با انجام استدلال مشابه، به فرمولی می رسیم که محاسبه انتگرال مضاعف را نیز به انتگرال مکرر کاهش می دهد. مثال 2. انتگرال دوگانه یک تابع را در ناحیه D. محاسبه کنید که با خطوط محدود شده است ^ راه اول. اجازه دهید منطقه انتگرال D را نشان دهیم. خط y = x و سهمی y = x2 در نقاطی قطع می شوند). این بدان معنی است که x در 8 حد از 0 تغییر می کند. هر خط مستقیم x = const) مرز منطقه را حداکثر در دو نقطه قطع می کند. بنابراین فرمول (8) قابل اجرا است: روش دوم (شکل 10). استفاده از فرمول (10). ما همان نتیجه را می گیریم: مثال 3. حجم جسم محدود شده به سطحی را محاسبه کنید که با صفحه xOy در امتداد خط بیضی با نیم محورها به دلیل تقارن این جسم نسبت به صفحات مختصات xOx و y قطع می شود، به دست می آوریم: تذکر دهید. اگر دامنه D به گونه ای باشد که برخی از خطوط مستقیم (اعم از متعامد یا افقی) مرز آن را در بیش از دو نقطه قطع کنند، برای محاسبه انتگرال دوگانه بر روی دامنه D، باید آن را به صورت مناسب به قطعات تقسیم کرد. ادغام انتگرال ها را به قطعات تکرار کنید و نتایج را اضافه کنید. مثال 4. اگر ضلع مربع داخلی 2 و انتگرال بیرونی 4 باشد، انتگرال دوگانه را روی مساحت D، محصور بین دو مربع با مرکز و در مبدا و اضلاع موازی با محورهای مختصات، محاسبه کنید. در مربع بزرگ Q که ضلع آن 4 است و در مربع کوچک R. که ضلع آن برابر با 2 است (شکل 12). طبق قضیه 1، انتگرال های تابع e*** بر روی مربع های نشان داده شده وجود دارند، به طوری که مقدار انتگرال مورد نظر §4 است. تغییر متغیرها در انتگرال دوگانه 4.1. مفهوم مختصات منحنی یک نقطه اجازه دهید یک جفت تابع در حوزه D* صفحه uOv داده شود که در این حوزه پیوسته و دارای مشتقات جزئی پیوسته در نظر می گیریم. به موجب رابطه (1)، هر نقطه M*(x,v) از ناحیه D* با یک نقطه معین M(x,y) در صفحه xOy مطابقت دارد و بنابراین با نقاط منطقه D* مطابقت دارد. مجموعه ای معین D از نقاط (x، y) در صفحه xy (شکل 13). در این مورد، گفته می شود که توابع (1) منطقه D4 را روی مجموعه D ترسیم می کنند. فرض کنید که نقاط مختلف (u، v) با نقاط مختلف (x، y) مطابقت دارند. این معادل حل‌پذیری منحصربه‌فرد معادلات (1) با توجه به u, v است: در این مورد، نگاشت، نگاشت یک به یک دامنه D* بر روی دامنه D نامیده می‌شود. تحت چنین تبدیلی، هر منحنی پیوسته L* که در دامنه D* قرار دارد به منحنی پیوسته L می رود که در ناحیه D قرار دارد. اگر توابع q(x) y) و h(x, y) نیز پیوسته باشند، هر LCD خط پیوسته با استفاده از تبدیل (2) از خط پیوسته L* C D* عبور خواهد کرد. برای یک جفت داده شده W, Vo از مقادیر متغیرهای u, v از ناحیه D*، می توان نه تنها موقعیت نقطه M*(u را به طور منحصر به فرد تعیین کرد.<)> Vq) در خود دامنه ξ)*، اما موقعیت نقطه متناظر M(xo، yo) در دامنه D، xo = 4>(o، v0)، 3/0 = o، vo). این زمینه را فراهم می کند تا اعداد u، v را به عنوان برخی مختصات جدید نقطه D ناحیه M در صفحه xOy در نظر بگیریم. به آنها مختصات منحنی نقطه M می گویند. مجموعه نقاط در منطقه D که یکی از مختصات آنها ثابت می ماند، خط مختصات نامیده می شود. با فرض فرمول (1) u = vq، معادلات پارامتری خط مختصات را بدست می آوریم، در اینجا نقش پارامتر توسط متغیر u ایفا می شود. با دادن مقادیر ثابت مختصات v (ممکن برای آن)، خانواده ای از خطوط مختصات (v = const) در صفحه xOy به دست می آوریم. به همین ترتیب، خانواده دیگری از خطوط مختصات را به دست می آوریم (u = const). اگر بین مناطق D* و D مطابقت یک به یک وجود داشته باشد، خطوط مختصات مختلف یک خانواده با یکدیگر تلاقی نمی کنند و یک خط از هر خانواده از هر نقطه ای از منطقه D می گذرد. شبکه خطوط مختصات منحنی در صفحه xOp تصویر یک شبکه مستطیل شکل در صفحه uOv است (شکل 13 را ببینید). 4.2. عنصر مساحت در مختصات منحنی. ژاکوبین و معنای هندسی آن اجازه دهید در ناحیه D* در صفحه Uo*V یک مستطیل کوچک P*P?P$Pl با اضلاع موازی با محورهای مختصات 0*u و O"v و طولهای آن مشخص کنیم. اضلاع Au و Av (برای قطعیت، به ترتیب A را فرض می کنیم) (شکل 14 الف). مساحت آن مستطیل به یک چهارضلعی منحنی * در ناحیه D تبدیل می شود (شکل 146). اگر راس های P دارای مختصات هستند، پس طبق فرمول (1)، رئوس مربوطه Pi دارای مختصات هستند)، با استفاده از فرمول تیلور برای تابعی از دو متغیر و محدود کردن خود به شرایط مرتبه اول / pc نسبت به Au و Av، به صورت تقریبی زیر را بدست می آوریم. مقادیر مختصات برای رئوس چهار ضلعی که در آن توابع، تمام مشتقات آنها در یک نقطه محاسبه می شود. ترتیب چهار ضلعی P\PiPiPa یک متوازی الاضلاع است. از نظر طول حاصلضرب برداری، مسئله منجر به مفهوم یک انتگرال دوگانه تعریف یک انتگرال مضاعف ویژگی های اساسی یک مساحت انتگرال دوگانه یک منطقه مسطح کاهش یک انتگرال دوگانه به یک تکرار شده تغییر متغیرها در انتگرال دوگانه عنصر مساحت در مختصات منحنی ژاکوبین و معنای هندسی آن تغییر فرمول متغیرها در انتگرال دوگانه انتگرال دوگانه در مختصات قطبی نقطه تعیین کننده (tx,v)) هنگامی که با استفاده از فرمول های تبدیل (1) روی دامنه D نگاشت می شود. 4.3. تغییر فرمول متغیرها در انتگرال دوگانه اجازه دهید توابع پیوسته نگاشت یک به یک دامنه D* را روی D انجام دهند و مشتقات جزئی پیوسته مرتبه اول داشته باشند. اجازه دهید یک تابع پیوسته در دامنه D در صفحه xOy داده شود. هر مقدار تابع) در دامنه D با مقدار مساوی تابع r = در دامنه D مطابقت دارد، جایی که (u، v) و (x) , y) به طوری که مقادیر توابع موجود در آنها منطبق باشد و مجموع انتگرال توابع z = /(x, y) و v) را روی دامنه های D و D * ترکیب می کنیم. ژاکوبین را به دست می آوریم. توابع (9) به حدی که بزرگترین قطر d* نواحی جزئی D\ به صفر میل می کند (به دلیل تداوم نقشه برداری (I)، بزرگترین قطر d نواحی جزئی در D نیز تمایل دارد. برای تبدیل انتگرال دوگانه در مختصات دکارتی به یک انتگرال مضاعف در مختصات منحنی، لازم است متغیرهای x و y را در انتگرال جایگزین کنیم. f(x, y)، به ترتیب، از طریق و عنصر مساحت dx dy - بیان آن در مختصات منحنی: مثال. مساحت یک شکل محدود شده با هذلول های m را پیدا کنید. مساحت شکل نشان داده شده به محاسبه یک انتگرال دوگانه بر روی منطقه O کاهش می یابد. اجازه دهید مختصات منحنی جدید u و o را با فرمول ها معرفی کنیم. این بدان معناست که در صفحه uOv یک مستطیل به دست آوردیم (شکل 156) - شکلی ساده تر از شکل D. بیایید x و y را از روابط (11) تا u و t> بیان کنیم: شکل 15 سپس انتگرال دوگانه در قطب مختصات محاسبه انتگرال دوگانه اغلب با جایگزینی مختصات مستطیلی x و y با مختصات قطبی طبق فرمول ساده می شود. عنصر مساحت در مختصات قطبی شکل و فرمول انتقال از انتگرال در مختصات دکارتی به انتگرال در مختصات قطبی را دارد. می توان به صورت زیر نوشت: در این مورد (13) عنصر مساحت در مختصات قطبی را می توان از ملاحظات هندسی به دست آورد (شکل 16 را ببینید). مساحت ناحیه سایه دار در شکل A \u003d pl. بخش ها سکتورها با حذف یک مقدار بینهایت کوچک از مرتبه بالاتر، عنصر منطقه را در مختصات قطبی به دست آورده و می پذیریم. بنابراین، برای تبدیل انتگرال دوگانه در مختصات دکارتی به انتگرال دوگانه در مختصات قطبی، باید a: و y را در انتگرال به ترتیب با p costp و psiny جایگزین کنید و عنصر مساحت در مختصات دکارتی dx dy را با مساحت جایگزین کنید. عنصر در مختصات قطبی p dp dip. اکنون اجازه دهید محاسبه انتگرال دوگانه در مختصات قطبی را در نظر بگیریم. همانطور که در مورد مختصات دکارتی مستطیلی، محاسبه انتگرال در مختصات قطبی با کاهش آن به یک انتگرال تکرار شده انجام می شود. اجازه دهید ابتدا موردی را در نظر بگیریم که قطب O خارج از ناحیه D قرار دارد. اجازه دهید ناحیه D این ویژگی را داشته باشد که هر پرتویی که از قطب ساطع می شود (خط مختصات y مرز خود را حداکثر در دو نقطه یا در امتداد یک قطعه کامل قطع می کند) شکل 17) توجه داشته باشید که مقادیر انتهایی i زاویه قطبی، حدود یکپارچگی خارجی هستند. نقاط Aw B کانتور ناحیه D را به دو قسمت تقسیم می کند: ACB و AFB. معادلات قطبی آنها را در نظر بگیرید، که در آن) توابع پیوسته تک مقداری هستند که شرایط را برآورده می کنند. با عبور از انتگرال های تکراری، فرمول زیر را به دست می آوریم به ویژه، برای ناحیه S دامنه D برای F(p, r 1 مرز منطقه را فقط در یک نقطه یا در امتداد کل قطعه به دست می آوریم (شکل 18) - معادله مرز منطقه در مختصات قطبی سپس شکل 18 مثال انتگرال را محاسبه کنید که در آن ناحیه یک چهارم دایره واحد واقع در ربع اول است بیایید به مختصات قطبی برویم سپس مساحت انتگرال یک است. مستطیل انتگرال تبدیل شده / به راحتی محاسبه می شود: r نکته: اگر ژاکوبین در دامنه D غیر صفر باشد، نگاشت در برخی از همسایگی های هر نقطه از این دامنه یک به یک است، اما ممکن است اتفاق بیفتد که نگاشت کل دامنه یک به یک نیست، اجازه دهید نگاشتی را در نظر بگیریم که توسط توابع تعریف شده است، ژاکوبین این توابع برابر است و بنابراین در همه جا غیر صفر است. با وجود این، برای ما دریافت می کنیم، بنابراین این نقشه برداری یک به یک نیست. از سوی دیگر، اگر ژاکوبین یک نقشه برداری در نقطه ای ناپدید شود، با این وجود، نقشه برداری در همسایگی این نقطه ممکن است یک به یک باشد. به عنوان مثال، برای نگاشتی که توسط توابع تعریف می شود، ژاکوبین برابر با صفر و در است، اما نگاشت یک به یک است. نگاشت معکوس توسط توابع تعریف می شود

1.1 تعریف انتگرال دوگانه

1.2 ویژگی های انتگرال دوگانه

خواص انتگرال مضاعف (و اشتقاق آنها) مشابه خواص متناظر انتگرال معین منفرد است.

1 درجه افزودنی. اگر تابع f(x,y) در حوزه D قابل ادغام باشد و اگر دامنه D با منحنی Γ ناحیه صفر به دو حوزه متصل D 1 و D 2 بدون نقاط داخلی مشترک تقسیم شود، تابع f(x، y) در هر یک از مناطق D 1 و D 2 قابل ادغام است و

2 درجه ویژگی خطی. اگر توابع f(x,y) و g(x,y) در دامنه D قابل ادغام باشند، ها؟ و - هر عدد واقعی، سپس تابع [؟ f(x, y) + ? g(x, y)] نیز در دامنه D قابل ادغام است و

3 درجه. اگر توابع f(x,y) و g(x,y) در دامنه D انتگرال پذیر باشند، حاصلضرب این توابع نیز در D قابل انتگرال است.

4 درجه اگر توابع f(x, y) و g(x, y) هر دو در دامنه D و همه جای این دامنه f(x, y) قابل ادغام هستند؟ g (x، y)، سپس

5 درجه. اگر تابع f(x,y) در دامنه D قابل ادغام باشد، تابع |f(x,y)| در دامنه D قابل ادغام است و

(البته، یکپارچگی |f(x,y)| در D به معنای یکپارچگی f(x,y) در D نیست.)

6 درجه قضیه مقدار میانگین. اگر هر دو تابع f(x,y) و g(x,y) در یک دامنه D ادغام شوند، تابع g(x,y) در همه جای این دامنه غیر منفی (غیر مثبت) است، M و m هستند. بهترین کران های بالا و پایین تابع f(x,y) در دامنه D، پس عددی وجود دارد که نابرابری m را برآورده می کند؟ ? ? M و به گونه ای که فرمول

به طور خاص، اگر تابع f(x، y) در D پیوسته باشد و دامنه D متصل باشد، در این حوزه چنین نقطه ای وجود دارد (?، ?)، چه؟ = f(?، ?)، و فرمول تبدیل می شود

7 درجه. یک ویژگی هندسی مهم برابر مساحت منطقه D

اجازه دهید یک جسم T در فضا داده شود (شکل 2.1)، که از پایین با ناحیه D محدود شده است، از بالا - با نمودار یک تابع پیوسته و غیر منفی) z \u003d f (x, y,) که تعریف شده است. در منطقه D، از طرفین - توسط یک سطح استوانه ای، که راهنمای آن محدوده مرزی D است، و ژنراتورها موازی با محور Oz هستند. به بدنه ای از این نوع بدنه استوانه ای می گویند.

1.3 تفسیر هندسی انتگرال دوگانه

1.4 مفهوم یک انتگرال دوگانه برای یک مستطیل

اجازه دهید یک تابع دلخواه f(x,y) در همه جای مستطیل تعریف شود R =؟ (شکل 1 را ببینید).

بیایید بخش a را تقسیم کنیم؟ ایکس؟ b با استفاده از نقاط a = x 0 به n بخش جزئی تبدیل شود< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

این تقسیم با استفاده از خطوط مستقیم موازی با محورهای Ox و Oy مربوط به تقسیم مستطیل R به n · p مستطیل جزئی R kl = ? (k = 1، 2، ...، n؛ l = 1، 2، ...، p). پارتیشن مشخص شده مستطیل R با نماد T نشان داده می شود. در ادامه، در این بخش، اصطلاح "مستطیل" به معنای مستطیلی است که اضلاع آن موازی با محورهای مختصات است.

روی هر مستطیل جزئی R kl، یک نقطه دلخواه (? k , ? l) انتخاب می کنیم. با قرار دادن?x k = x k - x k-1 ، ?y l = y l - y l-1 ، مساحت مستطیل را با R kl نشان می دهیم. بدیهی است که ?R kl = ?x k ?y l .

مجموع انتگرال تابع f(x,y) مربوط به یک پارتیشن معین T از مستطیل R و انتخاب معینی از نقاط میانی (?k، ?l) روی مستطیل های جزئی پارتیشن T نامیده می شود.

قطر مستطیل R kl نامیده می شود. یک نشانه؟ بزرگترین قطر تمام مستطیل های جزئی را نشان دهید R kl .

عدد I را حد مجموع انتگرال (1) می گویند؟ > 0 اگر برای هر عدد مثبت؟ آیا می توانید چنین عدد مثبتی را مشخص کنید؟، اگر چه؟< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - من |< ?.

تابع f(x, y) انتگرال پذیر (طبق نظر ریمان) روی مستطیل R نامیده می شود اگر یک حد محدود I از مجموع انتگرال این تابع در وجود داشته باشد؟ > 0.

این حد I انتگرال دوگانه تابع f(x,y) روی مستطیل R نامیده می شود و با یکی از نمادهای زیر نشان داده می شود:

اظهار نظر. همانطور که برای انتگرال معین یکباره، مشخص می شود که هر تابع f(x,y) قابل انتگرال در مستطیل R روی این مستطیل محدود می شود.

این زمینه را فراهم می‌کند که در موارد زیر فقط توابع محدود f(x,y) را در نظر بگیریم.

مسئله ای که منجر به مفهوم انتگرال دوگانه می شود.

فرض کنید تابعی از قطعات بر روی تعریف شده است و جمع را یادداشت کنید

که به آن انتگرال می گویند.

A: تحت یک انتگرال معین (d.i.) تابع و انتخاب

تعیین:

اعداد را ادغام پذیر می نامند (به گفته ریمان) در .

ت وجود: به شرطی که .

مطابق با تعریف o.i. توجه داشته باشید که انتگرال به شکل، حدود و

مطابق بندهای 17.1.1 و 17.1.2 و تعریف o.i. ما فرمول های مساحت ذوزنقه منحنی را می نویسیم: ، نیروی کار

بر :

مفهوم انتگرال دوگانه، مجموع انتگرال.

وجود یک انتگرال دوگانه، یعنی حد مجموع انتگرال برای آشکار به نظر می رسد، زیرا این حد حجم یک جسم استوانه ای را می دهد. با این حال، این استدلال دقیق نیست. در دروس کامل تر، این ادعا به طور دقیق اثبات می شود و قضیه وجود انتگرال مضاعف نامیده می شود.

قضیه وجود. برای هر تابعی که در یک ناحیه بسته محدود با مساحت a پیوسته است، یک انتگرال مضاعف وجود دارد، یعنی محدودیتی از مجموع انتگرال با افزایش نامحدود در تعداد ناحیه های کوچک وجود دارد، مشروط بر اینکه هر یک از آنها به یک نقطه منقبض شود. . این محدودیت نه به روش تقسیم منطقه به قطعات و نه به انتخاب نقاط بستگی دارد

در ادامه، تنها توابعی را در نظر خواهیم گرفت که در حوزه ادغام پیوسته هستند.

از قضیه وجود چنین برمی‌آید که مثلاً می‌توانیم ناحیه a را به مستطیل‌های کوچک با اضلاع مستقیم موازی با محورهای مختصات تقسیم کنیم (شکل 230). که در آن. سپس با انتخاب یک نقطه در هر مستطیل کوچک، می توانیم با توجه به تعریف انتگرال دوگانه بنویسیم

به منظور تأکید بر اینکه انتگرال دوگانه را می توان به عنوان حد مجموع فرم به دست آورد، به جای نماد، از نماد نیز استفاده می شود.

این عبارت در مختصات دکارتی عنصر مساحت نامیده می شود و برابر است با مساحت مستطیلی که اضلاع آن موازی با محورهای مختصات است.

توجه داشته باشید که هنگام جمع آوری مجموع انتگرال، نواحی مجاور مرز ناحیه a شکل مستطیل ندارند. با این حال، می‌توان ثابت کرد که خطای جایگزینی مستطیل‌هایی با مساحت‌های حد، به صفر می‌رسد.

ویژگی های انتگرال دوگانه

خواص انتگرال مضاعف (و اشتقاق آنها) مشابه خواص متناظر انتگرال معین منفرد است.

3 درجه. اگر توابع f(ایکس, y) و g(ایکس, y) در دامنه قابل ادغام هستند D، سپس محصول این توابع نیز قابل ادغام است D.

5 درجه. اگر تابع f(ایکس, y) در دامنه قابل ادغام است D، سپس تابع | f(ایکس, y)| قابل ادغام در منطقه D، و

(البته از یکپارچگی | f(ایکس, y)| V Dیکپارچگی به دنبال ندارد f(ایکس, y) V D.)

به ویژه، اگر تابع f(ایکس, y) پیوسته در است D، و منطقه D متصل، پس در این منطقه چنین نقطه ای وجود دارد ( ξ , η )، چی μ = f(ξ , η ، و فرمول (11) شکل می گیرد

برای تابعی از دو متغیر که به صورت تعریف شده است z = f(ایکس, y) .

انتگرال دوگانه به صورت زیر نوشته می شود:

اینجا D- یک شکل مسطح محدود شده با خطوط، که عبارات آن (برابری ها) در کار محاسبه انتگرال دوگانه آورده شده است. چپ و راست - برابری ها، که در آن متغیر در سمت چپ ایکس، و بالا و پایین - توسط برابری ها، که در آن متغیر در سمت چپ y. این مکان و بعد از آن یکی از مهمترین موارد برای درک تکنیک محاسبه انتگرال دوگانه است.

انتگرال دوگانه را محاسبه کنید - به معنای یافتن عددی برابر با مساحت شکل ذکر شده است D .

تا دست بزنیم تعاریف انتگرال دوگانه و محاسبه آن را یاد خواهیم گرفت. هنگامی که چندین مسئله برای محاسبه آن حل شده باشد، درک انتگرال دوگانه آسان تر است، بنابراین در پایان این درس، تعریف انتگرال دوگانه را خواهید یافت. با کمی نگاه کردن به آینده، فقط می توان به این نکته اشاره کرد که تعریف انتگرال دوگانه نیز با شکل ذکر شده همراه است. D .

اگر رقم Dیک مستطیل است، تمام خطوطی که آن را محدود می کنند، خطوط مستقیم هستند. اگر رقم D- منحنی، سپس در سمت چپ و در سمت راست با خطوط مستقیم محدود می شود، و از بالا و پایین - با خطوط منحنی داده شده توسط برابری های داده شده در کار. مواردی نیز وجود دارد که یک رقم D- یک مثلث، اما در مورد چنین مواردی کمی دورتر.

برای محاسبه انتگرال دوگانه، لازم است خطوط مرزی شکل را مرتب کنیم D، که نامی سخت دارد - منطقه ادغام. مرتب سازی به چپ و راست و بالا و پایین. این مورد نیاز خواهد بود زمانی که کاهش انتگرال دوگانه به انتگرال تکراری - روش محاسبه انتگرال دوگانه.

مورد مساحت مستطیلی:

مورد ناحیه منحنی:

و این در حال حاضر یک راه حل از انتگرال های مشخص آشنا برای ما است، که در آن حد بالا و پایین ادغام تنظیم شده است. عباراتی که خطوطی را تعریف می کنند که یک شکل را محدود می کنند D، حدود یکپارچه سازی برای انتگرال های معین معمولی خواهد بود که قبلاً به آنها نزدیک شده ایم.

کاهش انتگرال دوگانه به تکرار

مورد مساحت مستطیل شکل

اجازه دهید چنین تابعی یک انتگرال دوگانه داشته باشد

به این انتگرال دوگانه را محاسبه کنید ، باید آن را به انتگرال تکرار شده که دارای فرم است کاهش دهید

ابتدا باید انتگرال معین داخلی (راست) و سپس انتگرال معین بیرونی (چپ) را محاسبه کنید.

می توانید نقش ها را تغییر دهید ایکسو y

مثال 1انتگرال دوگانه را محاسبه کنید

ما انتگرال داخلی (راست) را با در نظر گرفتن y یک ثابت محاسبه می کنیم. دریافت می کنیم.

مثال 2انتگرال دوگانه را محاسبه کنید

راه حل. این انتگرال مضاعف را به انتگرال تکرار شده کاهش می دهیم

در نقاشی منطقه ادغام را می سازیم:

اکنون انتگرال بیرونی (چپ) را از انتگرال داخلی (راست) محاسبه می کنیم:

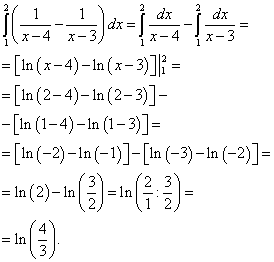
نتیجه حل این انتگرال دوگانه خواهد بود.

انتگرال دوگانه را خودتان محاسبه کنید و سپس جواب را ببینید

مورد ناحیه منحنی یا مثلثی

اجازه دهید دوباره تابعی از دو متغیر داده شود f(ایکس, y) ، و محدودیت برای D: ظاهر کمی متفاوت دارد:

این مدخل به این معنی است که شکل Dمحدودیت در سمت چپ و در سمت راست، همانطور که در مورد یک منطقه مستطیل - خطوط مستقیم ایکس = آو ایکس = ب، اما زیر و بالا منحنی هایی هستند که با معادلات و . به عبارت دیگر، و توابع هستند.

اجازه دهید چنین تابعی یک انتگرال دوگانه نیز داشته باشد

برای محاسبه این انتگرال مضاعف، باید آن را به انتگرال تکراری که دارای فرم است کاهش دهیم

اینجا محدودیت های ادغام است آو باعداد هستند و توابع هستند. در مورد یک منطقه مثلثی، یکی از توابع یا معادله یک خط مستقیم است. این مورد در مثال 3 مورد بحث قرار خواهد گرفت.

همانطور که در مورد یک ناحیه مستطیلی، ابتدا باید انتگرال قطعی راست و سپس انتگرال معین سمت چپ را محاسبه کنید.

شما همچنین می توانید نقش ها را به همین ترتیب تغییر دهید. ایکسو y. سپس انتگرال تکرار شده فرم خواهد داشت

چنین انتگرال تکرار شده باید دقیقاً به همان روش حل شود: ابتدا انتگرال داخلی (راست) و سپس بیرونی (چپ).

مثال 5انتگرال دوگانه را محاسبه کنید

راه حل. این انتگرال مضاعف را به انتگرال تکرار شده کاهش می دهیم

روی نقشه، ناحیه ادغام را می سازیم و می بینیم که مثلثی است:

ما انتگرال داخلی (راست) را با در نظر گرفتن x به عنوان یک ثابت محاسبه می کنیم. دریافت می کنیم.

اکنون انتگرال بیرونی (چپ) انتگرال داخلی (راست) محاسبه شده را محاسبه می کنیم. ابتدا این انتگرال را به صورت مجموع انتگرال ها نشان می دهیم:

ترم اول را محاسبه می کنیم:

ترم دوم را محاسبه می کنیم:

عبارت سوم را محاسبه می کنیم:

حاصل جمع را می گیریم که جواب این انتگرال دوگانه خواهد بود:

مثال 6انتگرال دوگانه را محاسبه کنید

راه حل. این انتگرال مضاعف را به انتگرال تکرار شده کاهش می دهیم

در نقاشی منطقه ادغام را می سازیم:

ما انتگرال داخلی (راست) را با در نظر گرفتن x به عنوان یک ثابت محاسبه می کنیم. دریافت می کنیم.

اکنون انتگرال بیرونی (چپ) را از انتگرال داخلی (راست) محاسبه می کنیم:

نتیجه حل این انتگرال دوگانه خواهد بود.

ایکس- درست و غلط y- حوزه های ادغام صحیح و نادرست

این اتفاق می افتد که ناحیه ادغام یک انتگرال مضاعف با چنین خطوطی محدود می شود که لازم است ناحیه ادغام به قطعات تقسیم شود و هر انتگرال تکرار شده مربوطه به طور جداگانه حل شود. اینها مواردی هستند که:

1) ناحیه ادغام شکلی است که دارای دو یا چند خط مستقیم یا منحنی به شکل مرز پایین یا بالا (چپ یا راست) است.

2) ناحیه ادغام شکلی است که مرزهای آن در بیش از دو نقطه قطع می شود.

اگر موارد فوق برای مرز چپ یا راست منطقه ادغام اعمال شود، یعنی محدودیت های داده شده توسط خطوط بیان شده از طریق ایکس، سپس دامنه ادغام نامیده می شود ایکس- اشتباه. اگر یک خط مستقیم y = y0 مرز مربوطه را فقط در یک نقطه قطع می کند، و اگر فقط یک خط یا منحنی به عنوان مرز عمل کند، منطقه ادغام نامیده می شود. ایکس-درست

به طور مشابه، اگر مرز تعریف شده توسط خطوط بیان شده بر حسب y، سر راست ایکس = ایکس0 در بیش از یک نقطه قطع می شود، یا اگر بیش از یک خط یا منحنی به عنوان مرز عمل می کند، منطقه ادغام نامیده می شود. y- اشتباه. اکنون علائم را بیاورید y-منطقه مناسب، احتمالاً کاملاً ساده.

تا اینجا نمونه هایی را در نظر گرفتیم ایکس- نادرست و y-مناطق منظم ادغام حال مواردی را در نظر بگیرید که شرط صحت نقض می شود.

مثال 7یک انتگرال دوگانه را محاسبه کنید که ناحیه ادغام آن توسط خطوط محدود شده است y = ایکس , xy = 1 , y = 2 .

راه حل. حوزه ادغام است y-نادرست است، زیرا مرز پایین آن را نمی توان با یک خط تنظیم کرد y = y(ایکس) . همانطور که در شکل بالا می بینید، کران پایینی از آن تشکیل شده است y = ایکس(رنگ قهوه ای تیره) و xy= 1 (سبز). بنابراین مستقیم ایکس= 1 (سیاه) می توانیم ناحیه ادغام را به دو قسمت تقسیم کنیم - و .

این انتگرال دوگانه به صورت زیر محاسبه می شود:

تغییر ترتیب ادغام

همانطور که در بالا ذکر شد، پس از کاهش انتگرال دوگانه به انتگرال تکراری، می توان متغیرها را تغییر داد. ایکسو yنقش ها یا به عبارت دیگر ترتیب ادغام را تغییر می دهند.

تغییر در ترتیب ادغام را می توان با کلمات زیر O "Henry" توصیف کرد: "ساکن جنگل اینگونه رفتار می کند - جانور که وارد قفس شده است و ساکن قفس اینگونه رفتار می کند. - مردی که در جنگل شک و تردید گم شده است.» نتیجه، همچنین به گفته او «هنری» یکی و یکسان است: «چالمرز نامه را به هزار تکه ریز پاره کرد و شروع به عذاب کشیدن فرش گران قیمت خود کرد و آن را به عقب برگرداند و به پیش." ( او.هنری. شهرزاده از میدان مدیسون.)

سپس، اگر انتگرال چپ را روی متغیر داشته باشیم ایکس، و حق y، پس از تغییر ترتیب ادغام، همه چیز برعکس خواهد بود. سپس حدود یکپارچه سازی برای y "جدید" باید از x "قدیمی" "قرض گرفته شود" و حدود ادغام برای x "جدید" باید به شکل به دست آید. تابع معکوس، حل معادله با توجه به x که حد را برای y تعیین می کند.

مثال 8

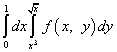راه حل. پس از تغییر ترتیب انتگرال، انتگرال روی y چپ و انتگرال روی x به سمت راست می شود. ما محدودیت های یکپارچه سازی بازیکن "جدید" را از X "قدیمی" قرض می گیریم، یعنی حد پایین برابر با صفر و حد بالایی برابر با یک است. حدود ادغام برای بازیکن "قدیمی" با معادلات و . پس از حل این معادلات با توجه به x، محدودیت های یکپارچه سازی جدیدی برای x بدست می آوریم:

(پایین) و (بالا).

بنابراین، پس از تغییر ترتیب ادغام، انتگرال تکرار شده به صورت زیر نوشته می شود:

پس از تغییر ترتیب ادغام در انتگرال دوگانه، دامنه ادغام اغلب به آن تبدیل می شود y- اشتباه یا ایکس- نادرست است (به پاراگراف قبلی مراجعه کنید). سپس لازم است ناحیه ادغام را به قطعات تقسیم کرده و هر انتگرال تکرار شده مربوطه را به طور جداگانه حل کنیم.

از آنجایی که تقسیم حوزه ادغام به بخش ها مشکلات خاصی را برای بسیاری از دانش آموزان ایجاد می کند، ما خود را به مثال ارائه شده در پاراگراف قبل محدود نمی کنیم، بلکه چند مثال دیگر را تحلیل خواهیم کرد.

مثال 9ترتیب ادغام را برای انتگرال تکرار شده تغییر دهید

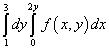راه حل. بنابراین، منطقه ادغام این انتگرال تکرار شده توسط خطوط مستقیم محدود می شود y = 1 , y = 3 , ایکس = 0 , ایکس = 2y .

هنگام ادغام به ترتیب متفاوت، مرز پایینی منطقه از دو خط مستقیم تشکیل شده است: ABو قبل از میلاد مسیح، که توسط معادلات به دست می آیند y= 1 و y = ایکس/2 که در شکل زیر قابل مشاهده است.

راه برون رفت از چنین عدم قطعیتی، تقسیم دامنه ادغام به دو بخش است. منطقه ادغام با یک خط مستقیم تقسیم می شود BM. حدود یکپارچه سازی جدید با یافتن تابع معکوس محاسبه می شود. بر اساس این راه حل، انتگرال تکرار شده پس از تغییر ترتیب انتگرال برابر با مجموع دو انتگرال خواهد بود:

به طور طبیعی، حل انتگرال دوگانه یکسان خواهد بود، که به انتگرال تکرار شده در شرایط این مثال کاهش می یابد.

مثال 10ترتیب ادغام را برای انتگرال تکرار شده تغییر دهید

راه حل. بنابراین، منطقه ادغام انتگرال تکرار شده توسط خطوط مستقیم محدود می شود ایکس = 0 , ایکس= 2 و منحنی و .

همانطور که در شکل زیر مشاهده می شود، یک خط مستقیم موازی با محور است 0x، مرز پایینی منطقه ادغام را در بیش از دو نقطه قطع خواهد کرد.

بنابراین دامنه ادغام را با خطوط مستقیم به سه قسمت تقسیم می کنیم که در شکل به رنگ مشکی ترسیم شده است. حدود یکپارچه سازی جدید با یافتن تابع معکوس محاسبه می شود. محدودیت برای سه حوزه جدید ادغام به شرح زیر خواهد بود.

بر اساس این راه حل، انتگرال مکرر پس از تغییر ترتیب انتگرال برابر با مجموع سه انتگرال خواهد بود:

مجموع یکسان سه انتگرال برابر با انتگرال مضاعف خواهد بود که به انتگرال تکرار شده در شرایط این مثال کاهش می یابد.

و با این حال، شرایط فورس ماژور اغلب با دانش آموزان در مرحله قبل تداخل می کند - تعیین محدودیت های ادغام. اضطراب و سردرگمی بدون پایه نیست: اگر معمولاً کافی است به نقاشی نگاه کنید تا حوزه ادغام را به قطعات تقسیم کنید و انتگرال تکراری - جدول انتگرال ها را حل کنید، در این صورت به تجربه آموزشی در تعیین حدود نیاز است. ادغام. بیایید مثالی را مرور کنیم که در آن فقط به ترتیب حدود ادغام و - تقریباً به طور خودکار - تقسیم منطقه می پردازیم و خود راه حل را حذف می کنیم.

مثال 11.حد ادغام یک انتگرال دوگانه را در صورت ناحیه ادغام پیدا کنید Dبه صورت زیر تنظیم کنید:

y - 2ایکس ≤ 0;
2 سال - ایکس ≥ 0;
xy ≤ 2.

راه حل. به صراحت (از طریق ایکسو y"بدون ناخالصی") خطوط محدود کننده منطقه ادغام مشخص نشده اند. از آنجایی که برای x اغلب آنها خطوط مستقیمی هستند که در یک نقطه مرزهای بالایی و پایینی بیان شده از طریق y را لمس می کنند، پس دقیقاً در این مسیر خواهیم رفت. علاوه بر این، هنگام تغییر ترتیب ادغام، یک ناحیه ادغام با همان ناحیه دریافت می کنیم. بیایید نابرابری های بازیکن را حل کنیم و بدست آوریم:

y ≤ 2ایکس;
y ≥ ایکس/2;
y ≤ 2/ایکس.

خطوط حاصل را روی نقاشی می سازیم. حدود ادغام با توجه به x در واقع خطوط هستند ایکس= 0 و ایکس= 2. اما منطقه ادغام معلوم شد y-نادرست است، زیرا مرز بالایی آن را نمی توان با یک خط تنظیم کرد y = y(ایکس) .

شاید خواندن آن مفید باشد: