Çünkü tutum. Sağ üçgen. Örneklerle ayrıntılı teori
Talimatlar
Yöntem 1. Pisagor teoremini kullanma. Teorem şunu belirtir: Hipotenüsün karesi, bacakların karelerinin toplamına eşittir. Bundan, bir dik üçgenin kenarlarından herhangi birinin, diğer iki kenarı bilinerek hesaplanabileceği sonucu çıkar (Şekil 2).
Yöntem 2. Ortancanın şu şekilde çizildiği gerçeğinden kaynaklanmaktadır: dik açı hipotenüse doğru kendi aralarında 3 benzer üçgen oluşturur (Şek. 3). Bu şekilde ABC, BCD ve ACD üçgenleri benzerdir.
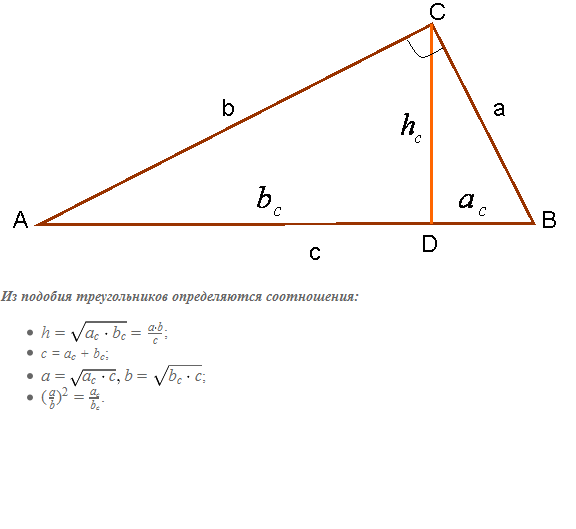
Hipotenüs, dik üçgende 90 derecelik açının karşısındaki kenardır. Uzunluğunu hesaplamak için bacaklardan birinin uzunluğunu ve üçgenin dar açılarından birinin boyutunu bilmek yeterlidir.

Talimatlar
Bilinen bir bacak ve bir dik üçgenin dar açısı göz önüne alındığında, hipotenüsün boyutu, bu açı ona karşıt/komşu ise, bacağın bu açının kosinüs/sinüs oranına eşit olabilir:
h = C1(veya C2)/sinα;
h = C1 (veya C2)/cosα.
Örnek: AB hipotenüsü ve C dik açısına sahip bir ABC dik üçgeni verilsin. B açısı 60 derece ve A açısı 30 derece olsun. BC kenarının uzunluğu 8 cm. AB hipotenüsünün uzunluğunu bulmamız gerekiyor. . Bunu yapmak için yukarıda önerilen yöntemlerden herhangi birini kullanabilirsiniz:
AB = BC/cos60 = 8 cm.
AB = BC/sin30 = 8 cm.
Hipotenüs, dik açının karşısında bulunan dik üçgenin tarafıdır. Bir dik üçgenin en uzun kenarıdır. Pisagor teoremi kullanılarak veya trigonometrik fonksiyonların formülleri kullanılarak hesaplanabilir.
![]()
Talimatlar
Dik üçgenin dik açıya bitişik kenarlarına bacak denir. Şekilde bacaklar AB ve BC olarak gösterilmiştir. Her iki bacağın uzunlukları verilsin. Bunları |AB| olarak gösterelim. ve |BC|. |AC| hipotenüsünün uzunluğunu bulmak için Pisagor teoremini kullanırız. Bu teoreme göre bacakların karelerinin toplamı hipotenüsün karesine eşittir; şeklimizin gösteriminde |AB|^2 + |BC|^2 = |AC|^2. Formülden AC hipotenüsünün uzunluğunun |AC| = √(|AB|^2 + |BC|^2) .
Bir örneğe bakalım. Bacakların uzunlukları |AB| olsun = 13, |BC| = 21. Pisagor teoremini kullanarak |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610 olduğunu buluruz. Hipotenüsün uzunluğunu elde etmek için, şunun karekökünü çıkarmak gerekir: bacakların karelerinin toplamı, yani. 610 numaradan: |AC| = √610. Tam sayıların kareleri tablosunu kullanarak 610 sayısının herhangi bir tam sayının tam karesi olmadığını buluruz. Hipotenüs uzunluğunun nihai değerini elde etmek için kök işaretinin altındaki tam kareyi çıkarmaya çalışalım. Bunu yapmak için 610 sayısını çarpanlarına ayıralım. 610 = 2*5*61. Tabloya göre asal sayılar 61'in asal sayı olduğunu görelim. Bu nedenle √610 sayısının daha da azaltılması mümkün değildir. Son cevabı alıyoruz |AC| = √610.
Hipotenüsün karesi örneğin 675 olsaydı, o zaman √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. Böyle bir azalma mümkünse, sonucun karesini alarak ters bir kontrol yapın ve bunu orijinal değerle karşılaştırın.
Bacaklardan birini ve ona bitişik açıyı bize bildirin. Daha spesifik olmak gerekirse, bunlar |AB| tarafı olsun. ve açı α. Daha sonra trigonometrik fonksiyon kosinüs formülünü kullanabiliriz - bir açının kosinüsü, bitişik kenarın hipotenüse oranına eşittir. Onlar. gösterimimizde çünkü α = |AB| / |AC|. Buradan |AC| hipotenüsünün uzunluğunu elde ederiz. = |AB| / çünkü α.
|BC| tarafını biliyorsak ve açı α ise, açının sinüsünü hesaplamak için formülü kullanacağız - açının sinüsü karşı kenarın hipotenüse oranına eşittir: sin α = |BC| / |AC|. Hipotenüs uzunluğunun |AC| olduğunu buluyoruz. = |BC| / çünkü α.
Açıklık sağlamak için bir örneğe bakalım. Bacağın uzunluğu |AB| verilsin. = 15. Ve α açısı = 60°. |AC| elde ederiz = 15 / çünkü 60° = 15 / 0,5 = 30.
Pisagor teoremini kullanarak sonucunuzu nasıl kontrol edebileceğinize bakalım. Bunu yapmak için ikinci bacağın |BC| uzunluğunu hesaplamamız gerekiyor. tan açısının tanjantı formülünü kullanma α = |BC| / |AC|, |BC|'yi elde ederiz = |AB| * ten rengi α = 15 * ten rengi 60° = 15 * √3. Daha sonra Pisagor teoremini uygularsak 15^2 + (15 * √3)^2 = 30^2 => 225 + 675 = 900 elde ederiz. Kontrol tamamlandı.
Hipotenüsü hesapladıktan sonra elde edilen değerin Pisagor teoremini karşılayıp karşılamadığını kontrol edin.
Kaynaklar:
- 1'den 10000'e kadar asal sayılar tablosu
Bacaklar boyutu 90° olan tepe noktasını oluşturan dik üçgenin iki kısa kenarıdır. Böyle bir üçgenin üçüncü kenarına hipotenüs denir. Üçgenin tüm bu kenarları ve açıları, diğer birkaç parametre biliniyorsa bacağın uzunluğunu hesaplamayı mümkün kılan belirli ilişkilerle birbirine bağlanır.

Talimatlar
Bir dik üçgenin diğer iki tarafının (B ve C) uzunlukları biliniyorsa, (A) bacağının uzunluğunu hesaplamak için Pisagor Teoremini kullanın. Bu teorem, bacakların kare uzunluklarının toplamının hipotenüsün karesine eşit olduğunu belirtir. Bundan, her bir kenarın uzunluğunun, hipotenüs ile ikinci kenarın uzunluklarının kareleri arasındaki farkın kareköküne eşit olduğu sonucu çıkar: A=√(C²-B²).
Hesaplanan bacağın karşısındaki açının (α) büyüklüğünü ve hipotenüsün uzunluğunu (C) biliyorsanız, dar açı için doğrudan trigonometrik fonksiyon "sinüs" tanımını kullanın. Bu tanım şunu belirtir: bunun sinüsü bilinen açı istenilen bacağın uzunluğunun hipotenüs uzunluğuna oranına eşittir. Bu, istenen kenarın uzunluğunun hipotenüs uzunluğu ile bilinen açının sinüsünün çarpımına eşit olduğu anlamına gelir: A=C∗sin(α). Bilinen aynı büyüklükler için kosekant fonksiyonunun tanımını da kullanabilir ve hipotenüsün uzunluğunu bilinen A=C/cosec(α) açısının kosekantına bölerek gereken uzunluğu hesaplayabilirsiniz.
Hipotenüs uzunluğuna (C) ek olarak istenen ayağa bitişik dar açının (β) büyüklüğü de biliniyorsa, doğrudan trigonometrik kosinüs fonksiyonunun tanımını kullanın. Bu açının kosinüsü, istenilen kenarın uzunluklarının hipotenüse oranı olarak tanımlanır ve bundan, bacağın uzunluğunun hipotenüs uzunluğu ile bilinenin kosinüsünün çarpımına eşit olduğu sonucuna varabiliriz. açı: A=C∗cos(β). Sekant fonksiyonunun tanımını kullanabilir ve hipotenüsün uzunluğunu bilinen A=C/sn(β) açısının sekantına bölerek istenen değeri hesaplayabilirsiniz.
İstenilen bacağın (A) karşısındaki dar açının (a) değerine ek olarak ikinci bacağın (B) uzunluğu biliniyorsa, trigonometrik fonksiyonun teğetinin türevi için benzer bir tanımdan gerekli formülü türetin. . İstenilen bacağın karşısındaki açının tanjantı, bu bacağın uzunluğunun ikinci bacağın uzunluğuna oranıdır. Bu, istenen değerin bilinen bacağın uzunluğu ile bilinen açının tanjantının çarpımına eşit olacağı anlamına gelir: A=B∗tg(α). Kotanjant fonksiyonunun tanımını kullanırsak, bu bilinen niceliklerden başka bir formül türetilebilir. Bu durumda bacağın uzunluğunu hesaplamak için bilinen bacağın uzunluğunun bilinen açının kotanjantına oranını bulmak gerekecektir: A=B/ctg(α).
Konuyla ilgili video
"Kathet" kelimesi Yunancadan Rusça'ya geldi. Tam tercümede, çekül hattı anlamına gelir, yani dünya yüzeyine dik. Matematikte bacaklar dik bir üçgenin dik açısını oluşturan kenarlardır. Bu açının karşısındaki kenara hipotenüs denir. “Katet” terimi mimaride ve kaynak teknolojisinde de kullanılmaktadır.

Bir dik üçgen DIA çizin. Bacaklarını a ve b, hipotenüsünü ise c olarak etiketleyin. Bir dik üçgenin tüm kenarları ve açıları belirli ilişkilerle birbirine bağlıdır. Akut açılardan birinin karşısındaki bacağın hipotenüse oranına bu açının sinüsü denir. Bu üçgende sinCAB=a/c. Kosinüs, bitişik bacağın hipotenüsüne olan orandır, yani cosCAB=b/c. Ters ilişkilere sekant ve kosekant denir.
Bu açının sekantı, hipotenüsün bitişik kenara bölünmesiyle elde edilir, yani secCAB = c/b. Sonuç kosinüsün tersidir, yani secCAB=1/cosSAB formülü kullanılarak ifade edilebilir.
Kosekant, hipotenüsün karşı tarafa bölünmesine eşittir ve sinüsün tersidir. cosecCAB=1/sinCAB formülü kullanılarak hesaplanabilir.
Her iki bacak da teğet ve kotanjant ile bağlanır. İÇİNDE bu durumda teğet, a tarafının b tarafına, yani karşı tarafın bitişik kenara oranı olacaktır. Bu ilişki tgCAB=a/b formülüyle ifade edilebilir. Buna göre ters oran kotanjant olacaktır: ctgCAB=b/a.
Hipotenüsün boyutları ile her iki bacak arasındaki ilişki eski Yunan matematikçi Pisagor tarafından belirlendi. İnsanlar hala onun adını taşıyan teoremi kullanıyor. Hipotenüsün karesinin kenarların karelerinin toplamına eşit olduğunu söylüyor, yani c2 = a2 + b2. Buna göre her bir bacak, hipotenüsün kareleri ile diğer bacağın kareleri arasındaki farkın kareköküne eşit olacaktır. Bu formül b=√(c2-a2) şeklinde yazılabilir.
Bacağın uzunluğu sizin bildiğiniz ilişkilerle de ifade edilebilir. Sinüs ve kosinüs teoremlerine göre bir bacak, hipotenüsün ve bu fonksiyonlardan birinin çarpımına eşittir. Ayrıca teğet veya kotanjant yoluyla da ifade edilebilir. A ayağı, örneğin a = b*tan CAB formülü kullanılarak bulunabilir. Aynı şekilde verilen teğet veya kotanjanta bağlı olarak ikinci bacak belirlenir.
"Katet" terimi mimaride de kullanılmaktadır. İyonik bir başkente uygulanır ve sırtının ortasından geçen bir çekül çizgisini belirtir. Yani bu durumda bu terim belirli bir çizgiye dik olanı ifade eder.
Kaynak teknolojisinde “fileto kaynak ayağı” kavramı vardır. Diğer durumlarda olduğu gibi bu en kısa mesafedir. Burada Hakkında konuşuyoruz kaynak yapılan parçalardan biri ile diğer parçanın yüzeyinde bulunan dikişin sınırı arasındaki boşluk hakkında.
Konuyla ilgili video
Kaynaklar:
- kenar ve hipotenüs nedir?
Konuyla ilgili video
Not
Bir dik üçgenin kenarlarını hesaplarken, özelliklerine ilişkin bilgi önemli bir rol oynayabilir:
1) Bir dik açının kenarı 30 derecelik bir açının karşısında yer alıyorsa, hipotenüsün yarısına eşittir;
2) Hipotenüs her zaman bacakların herhangi birinden daha uzundur;
3) Bir dik üçgenin çevresine bir daire çevrelenmişse, merkezi hipotenüsün ortasında olmalıdır.
Trigonometri, trigonometrik fonksiyonları ve bunların pratik kullanımını inceleyen bir matematik dalıdır. Bu tür işlevler şunları içerir: sinüs, kosinüs, teğet ve kotanjant.
Sinüs trigonometrik fonksiyon , karşı bacağın boyutunun hipotenüs boyutuna oranı.
Trigonometride sinüs.
Yukarıda belirtildiği gibi sinüs, trigonometri ve trigonometrik fonksiyonlarla doğrudan ilgilidir. İşlevi şu şekilde belirlenir:
- üçgenin kenarlarının boyutlarının bilinmesi koşuluyla açının hesaplanmasına yardımcı olun;
- Açının bilinmesi koşuluyla bir üçgenin kenarlarının hesaplanmasına yardımcı olur.
Sinüs bir ölçüm değil, oran olduğundan, sinüs değerinin üçgenin herhangi bir boyutu için her zaman aynı olacağı unutulmamalıdır.
Sonuç olarak belirli bir problemin her çözümü için bu sabit değeri hesaplamamak amacıyla özel trigonometrik tablolar oluşturulmuştur. Bunlarda sinüs, kosinüs, teğet ve kotanjant değerleri zaten hesaplanmış ve sabitlenmiştir. Genellikle bu tablolar cebir ve geometri ders kitaplarının ön sayfalarında verilmektedir. İnternette de bulunabilirler.
Geometride sinüs.
Geometri netlik gerektirir, bu nedenle pratikte anlamak için bir açının sinüsü nedir, dik açılı bir üçgen çizmeniz gerekir.
Bir dik açı oluşturan kenarların isimlendirildiğini varsayalım. AC, onların karşısındaki açı - X.
Genellikle ödevler kenarların uzunluğunu gösterir. Diyelimki a=3, b=4. Bu durumda en boy oranı ¾ gibi görünecektir. Üstelik üçgenin dar açıya bitişik kenarlarını uzatırsanız X, sonra kenarlar artacak A Ve V ve hipotenüs, dik bir üçgenin tabana dik olmayan üçüncü tarafıdır. Artık üçgenin kenarları farklı şekilde çağrılabilir, örneğin: m, n, k.
Bu değişiklikle trigonometri yasası işe yaradı: Üçgenin kenarlarının uzunlukları değişti, ancak oranları değişmedi.
Bir üçgenin kenarlarının uzunluğu herhangi bir sayıda değiştiğinde ve x açısının değeri korunurken kenarları arasındaki oranın hala değişmeden kalacağı gerçeği eski bilim adamları tarafından fark edildi. Bizim durumumuzda kenar uzunlukları şu şekilde değişebilir: a/b = ¾, tarafı uzatırken A 6 cm'ye kadar ve V– 8 cm'ye kadar şunu elde ederiz: m/n = 6/8 = 3/4.
Bu nedenle bir dik üçgendeki en boy oranlarına şu ad verilir:
- x açısının sinüsü karşı tarafın hipotenüse oranıdır: sinx = a/c;
- x açısının kosinüsü, bitişik kenarın hipotenüse oranıdır: cosx = b/c;
- x açısının tanjantı, karşı bacağın bitişik olana oranıdır: tgx = a/b;
- x açısının kotanjantı, komşu kenarın karşı kenara oranıdır: ctgx = b/a.
Trigonometri çalışmamıza dik üçgenle başlayacağız. Bir akut açının teğet ve kotanjantının yanı sıra sinüs ve kosinüsün ne olduğunu tanımlayalım. Bu trigonometrinin temelidir.
şunu hatırlatalım dik açı eşit bir açıdır. Başka bir deyişle, yarım dönmüş bir açı.
Keskin köşe- daha küçük.
Geniş açı- daha büyük. Böyle bir açıyla ilgili olarak "geniş" hakaret değil matematiksel bir terimdir :-)

Bir dik üçgen çizelim. Dik açı genellikle ile gösterilir. Lütfen köşenin karşısındaki tarafın aynı harfle, yalnızca küçük olarak gösterildiğini unutmayın. Böylece açının karşısındaki taraf belirlenir.
Açı karşılık gelen Yunanca harfle gösterilir.
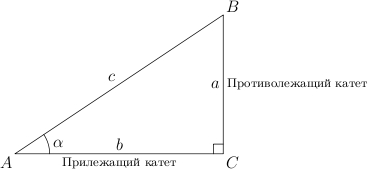
Hipotenüs Bir dik üçgenin dik açının karşısındaki kenardır.
Bacaklar- dar açıların karşısında yer alan kenarlar.
Açının karşısında uzanan bacağa denir zıt(açıya göre). Açının kenarlarından birinde yer alan diğer bacağa denir. bitişik.
Sinüs Bir dik üçgende dar açı, karşı kenarın hipotenüse oranıdır:
Kosinüs Dik üçgende dar açı - bitişik bacağın hipotenüse oranı:
Teğet dik üçgende dar açı - karşı tarafın bitişik tarafa oranı:
Başka bir (eşdeğer) tanım: bir dar açının tanjantı, açının sinüsünün kosinüsüne oranıdır:
![]()
Kotanjant dik üçgende dar açı - bitişik tarafın karşı tarafa oranı (veya aynı şekilde kosinüsün sinüse oranı):
![]()
Aşağıdaki sinüs, kosinüs, teğet ve kotanjant için temel ilişkilere dikkat edin. Sorunları çözerken bize faydalı olacaklar.
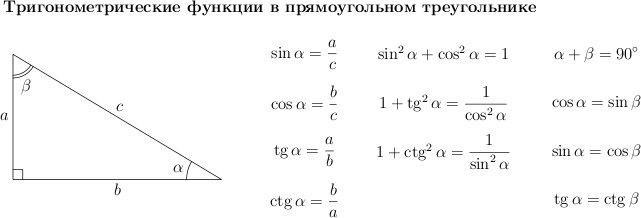
Bunlardan bazılarını kanıtlayalım.
1. Herhangi bir üçgenin açılarının toplamı eşittir. Araç, bir dik üçgenin iki dar açısının toplamı eşittir .
2. Bir tarafta karşı tarafın hipotenüse oranı. Öte yandan, açı nedeniyle bacak bitişik olacaktır.
Bunu anlıyoruz ![]() . Başka bir deyişle, .
. Başka bir deyişle, .
3. Pisagor teoremini alın: ![]() . Her iki parçayı da şuna bölelim:
. Her iki parçayı da şuna bölelim:
![]()
Aldık temel trigonometrik kimlik:
Böylece bir açının sinüsünü bilerek kosinüsünü bulabiliriz ve bunun tersi de geçerlidir.
4. Ana trigonometrik özdeşliğin her iki tarafını da bölerek şunu elde ederiz:
![]()
Bu, bize bir dar açının tanjantı verilirse kosinüsünü hemen bulabileceğimiz anlamına gelir.
Aynı şekilde,
![]()
Tamam, tanımları verdik ve formülleri yazdık. Peki neden hala sinüs, kosinüs, teğet ve kotanjanta ihtiyacımız var?
Biz biliyoruz ki herhangi bir üçgenin açılarının toplamı eşittir.
arasındaki ilişkiyi biliyoruz. partiler sağ üçgen. Bu Pisagor teoremidir: ![]() .
.
Bir üçgendeki iki açıyı bilerek üçüncüyü bulabileceğiniz ortaya çıktı. Dik üçgenin iki kenarını bilerek üçüncüsünü bulabilirsiniz. Bu, açıların kendi oranlarına ve kenarların kendilerine ait olduğu anlamına gelir. Peki bir dik üçgende bir açıyı (dik açı hariç) ve bir kenarı biliyorsanız ancak diğer kenarları bulmanız gerekiyorsa ne yapmalısınız?
Sinüs ve kosinüs başlangıçta dik üçgenlerdeki miktarları hesaplama ihtiyacından doğmuştur. Bir dik üçgende açıların derece ölçüsü değiştirilmezse, bu kenarların uzunluğu ne kadar değişirse değişsin en boy oranının daima aynı kaldığı fark edildi.Sinüs ve kosinüs kavramları bu şekilde tanıtıldı. Bir dik üçgende dar açının sinüsü, karşı tarafın hipotenüse oranıdır ve kosinüs, hipotenüse komşu olan tarafın oranıdır.
Kosinüs ve sinüs teoremleri
Ancak kosinüsler ve sinüsler dik üçgenlerden daha fazlası için kullanılabilir. Herhangi bir üçgenin geniş veya dar açısının veya kenarının değerini bulmak için kosinüs ve sinüs teoremini uygulamak yeterlidir.Kosinüs teoremi oldukça basittir: "Bir üçgenin bir kenarının karesi, diğer iki kenarın karelerinin toplamından bu kenarların çarpımının iki katı ve aralarındaki açının kosinüsüne eşittir."
Sinüs teoreminin iki yorumu vardır: küçük ve genişletilmiş. Minöre göre: “Bir üçgende açılar karşı kenarlarla orantılıdır.” Bu teorem genellikle bir üçgenin çevrelenmiş dairesinin özelliği nedeniyle genişletilir: "Bir üçgende açılar karşıt kenarlarla orantılıdır ve bunların oranı çevrelenen dairenin çapına eşittir."
Türevler
Türev, bir fonksiyonun argümanındaki değişikliğe göre ne kadar hızlı değiştiğini gösteren matematiksel bir araçtır. Türevler cebirde, geometride, ekonomide, fizikte ve bir takım teknik disiplinlerde kullanılmaktadır.Problemleri çözerken trigonometrik fonksiyonların türevlerinin tablo değerlerini bilmeniz gerekir: sinüs ve kosinüs. Sinüsün türevi kosinüstür ve kosinüs sinüstür ancak eksi işareti vardır.
Matematikte uygulama
Sinüsler ve kosinüsler özellikle dik üçgenlerin ve bunlarla ilgili problemlerin çözümünde sıklıkla kullanılır.Sinüs ve kosinüslerin rahatlığı teknolojiye de yansır. Karmaşık şekilleri ve nesneleri "basit" üçgenlere ayıran kosinüs ve sinüs teoremlerini kullanarak açıları ve kenarları değerlendirmek kolaydı. Çoğunlukla en boy oranları ve derecelerin hesaplanmasıyla uğraşan mühendisler ve mimarlar, tablo dışı açıların kosinüslerini ve sinüslerini hesaplamak için çok fazla zaman ve çaba harcadılar.
Daha sonra binlerce sinüs, kosinüs, teğet ve farklı açılardan kotanjant değerlerini içeren Bradis tabloları kurtarmaya geldi. İÇİNDE Sovyet zamanı bazı öğretmenler öğrencilerini Bradis tablolarının sayfalarını ezberlemeye zorladı.
Çokgenlerin en basiti olan sağ üçgen üzerinde, matematiğin bu alanını kimsenin bu kelimeyle adlandırmadığı günlerde, çeşitli bilim adamları trigonometri alanındaki bilgilerini geliştirdiler. Dolayısıyla bugün bu düz geometrik şeklin kenar uzunlukları ve açı değerleri oranlarındaki desenleri tespit eden yazarı belirtmek mümkün değildir. Bu tür ilişkilere trigonometrik fonksiyonlar denir ve ana hatları geleneksel olarak "doğrudan" fonksiyonlar olarak kabul edilen birkaç gruba ayrılır. Bu grup sadece iki fonksiyon içerir ve bunlardan biri sinüstür.
Talimatlar
Tanım gereği bir dik üçgende açılardan biri 90°'ye eşittir ve Öklid geometrisindeki açılarının toplamının 180° olması gerektiğinden diğer iki açı dardır (yani 90°'den küçüktür). °). Tam olarak bu açılar ve kenar uzunlukları arasındaki ilişki kalıpları trigonometrik fonksiyonları tanımlar.
Akut açının sinüsü adı verilen bir fonksiyon, bir dik üçgenin, biri dar açının karşısında, diğeri ona bitişik ve dik açının karşısında yer alan iki tarafının uzunlukları arasındaki oranı belirler. Böyle bir üçgende dik açının karşısındaki tarafa hipotenüs, diğer ikisine ise kenar adı verildiğinden, sinüs fonksiyonunun tanımı, karşı kenarın uzunlukları ile hipotenüs arasındaki oran olarak formüle edilebilir.
Bu trigonometrik fonksiyonun bu en basit tanımına ek olarak, bugün daha karmaşık olanları da var: Kartezyen koordinatlardaki bir daire aracılığıyla, seriler yoluyla, diferansiyel ve fonksiyonel denklemlerin çözümleri aracılığıyla. Bu fonksiyon süreklidir, yani argümanları (“alan”) sonsuz negatiften sonsuz pozitife kadar herhangi bir sayı olabilir. Ve bu fonksiyonun maksimum ve minimum değerleri -1 ila +1 aralığıyla sınırlıdır - bu "değer aralığıdır". Sinüs minimum değerini Pi'nin 3/2'sine karşılık gelen 270°'lik bir açıda alır ve maksimum değeri 90°'de (Pi'nin ½'si) elde edilir. Fonksiyon değerleri 0°, 180°, 360° vb. açılarda sıfır olur. Bütün bunlardan sinüsün periyodik bir fonksiyon olduğu ve periyodunun 360°'ye veya Pi sayısının iki katına eşit olduğu sonucu çıkar.
Bu işlevin değerlerinin belirli bir argümandan pratik hesaplamaları için, bir hesap makinesi kullanabilirsiniz - bunların büyük çoğunluğu (yerleşik hesap makinesi yazılımı dahil) işletim sistemi Bilgisayarınız) uygun bir seçeneğe sahiptir.
Konuyla ilgili video
Talimatlar
açı bir dik üçgende kosinüs tanımını kullanmanız ve bitişik kenarın hipotenüse oranını bulmanız gerekir:
çünkü? = a/c, burada a bacağın uzunluğu, c ise hipotenüsün uzunluğudur.
Kosinüsü bulmanız gerekiyorsa açı rastgele bir üçgende kosinüs teoremini kullanmanız gerekir:
açı dar ise: çünkü? = (a2 + b2 – c2)/(2ab);
açı genişse: çünkü? = (c2 – a2 – b2)/(2ab), burada a, b köşeye bitişik kenarların uzunluklarıdır, c ise köşenin karşısındaki kenarın uzunluğudur.
Kosinüsü bulmanız gerekiyorsa açı keyfi bir geometrik şekilde değeri belirlemek gerekir açı derece veya radyan ve kosinüs cinsinden açı Bir mühendislik hesap makinesi, Bradis tabloları veya başka herhangi bir matematiksel uygulamayı kullanarak değerine göre bulun.
Kosinüs açının temel bir trigonometrik fonksiyonudur. Kosinüs belirleme yeteneği, vektör cebirinde, vektörlerin çeşitli eksenlere izdüşümü belirlenirken faydalıdır.
Talimatlar
сos?=(b?+c?-a?)/(2*b*c)
A, b, c kenarları sırasıyla 3, 4, 5 mm'ye eşit olan bir üçgen vardır.
Bulmak kosinüs büyük kenarlar arasındaki açı.
a kenarının karşısındaki açıyı ? ile gösterelim, o zaman yukarıda türetilen formüle göre şunu elde ederiz:
сos?=(b?+c?-a?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 =32/40=0,8
Cevap: 0,8.
Üçgen dik açılı ise, o zaman bulmak için kosinüs ve bir açı için herhangi iki kenarın uzunluğunu bilmek yeterlidir ( kosinüs dik açı 0'dır).
Kenarları a, b, c olan ve c hipotenüs olan bir dik üçgen olsun.
Tüm seçenekleri ele alalım:
a ve b kenarlarının uzunlukları (üçgenin bacakları) biliniyorsa cos'u bulun?
Ek olarak Pisagor teoremini kullanalım:
сos?=(b?+c?-а?)/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?)) =(2*b?)/(2*b*v(b?+a?))=b/v(b?+a?)
Ortaya çıkan formülün doğruluğunu kontrol etmek için örnek 1'deki değerleri yerine koyalım, yani.
Bazı temel hesaplamalar yaptıktan sonra şunu elde ederiz:
Benzer şekilde bulundu kosinüs dikdörtgen şeklinde üçgen diğer durumlarda:
a ve c (hipotenüs ve karşı kenar) biliniyorsa cos'u bulun?
сos?=(b?+c?-а?)/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?)) =(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
İlk örnekteki a=3 ve c=5 değerlerini değiştirerek şunu elde ederiz:
Bilinen b ve c (hipotenüs ve bitişik bacak).
Çünkü buldun mu?
Benzer dönüşümleri yaptıktan sonra (örnek 2 ve 3'te gösterilmiştir), bu durumda şunu elde ederiz: kosinüs V üçgençok basit bir formül kullanılarak hesaplanır:
Türetilmiş formülün basitliği basitçe açıklanabilir: aslında köşeye bitişik mi? bacak hipotenüsün bir izdüşümüdür, dolayısıyla uzunluğu hipotenüs uzunluğunun cos? ile çarpımına eşittir.
İlk örnekteki b=4 ve c=5 değerlerini değiştirerek şunu elde ederiz:
Bu, tüm formüllerimizin doğru olduğu anlamına gelir.
İpucu 5: Dik üçgende dar açı nasıl bulunur?
Direkt olarak karboniküçgen muhtemelen tarihsel açıdan en ünlü olanlardan biridir, geometrik şekiller. Pisagorcu “pantolon” ancak “Eureka!” ile rekabet edebilir. Arşimet.

İhtiyacın olacak
- - bir üçgenin çizimi;
- - cetvel;
- - iletki
Talimatlar
Bir üçgenin açılarının toplamı 180 derecedir. Dikdörtgen şeklinde üçgen bir açı (düz) her zaman 90 derece olacaktır ve geri kalanı dardır, yani. her biri 90 dereceden az. Dikdörtgende hangi açının olduğunu belirlemek için üçgen Düz ise üçgenin kenarlarını ölçmek ve en büyüğünü belirlemek için bir cetvel kullanın. Buna hipotenüs (AB) denir ve dik açının (C) karşısında bulunur. Geriye kalan iki kenar dik açı oluşturur ve bacaklar (AC, BC) olarak adlandırılır.
Hangi açının dar açı olduğunu belirledikten sonra açıyı açıölçer kullanarak ölçebilir veya matematik formüllerini kullanarak hesaplayabilirsiniz.
Açıölçer kullanarak açıyı belirlemek için, üst kısmını (bunu A harfiyle gösterelim) iletkinin ortasındaki cetvel üzerindeki özel işaretle hizalayın; AC bacağı üst kenarıyla çakışmalıdır. İletkinin yarım daire şeklindeki kısmına AB hipotenüsünün geçtiği noktayı işaretleyin. Bu noktadaki değer derece cinsinden açıya karşılık gelir. İletken üzerinde belirtilen 2 değer varsa, o zaman dar bir açı için daha küçük olanı, geniş bir açı için - daha büyük olanı seçmeniz gerekir.
Ortaya çıkan değeri Bradis referans tablolarında bulun ve sonuç değerinin hangi açıya karşılık geldiğini belirleyin Sayısal değer. Büyükannelerimiz bu yöntemi kullanırdı.
Günümüzde trigonometrik formülleri hesaplama işlevine sahip bir hesap makinesi almak yeterlidir. Örneğin, yerleşik Windows hesap makinesi. "Hesap Makinesi" uygulamasını başlatın, "Görünüm" menü öğesinden "Mühendislik" seçeneğini seçin. İstediğiniz açının sinüsünü hesaplayın; örneğin sin (A) = BC/AB = 2/4 = 0,5
Hesap makinesi ekranındaki INV düğmesine tıklayarak hesap makinesini ters fonksiyonlar moduna geçirin, ardından arksinüs fonksiyonunu hesaplamak için düğmeye tıklayın (ekranda sin üzeri eksi birinci kuvvet olarak gösterilir). Hesaplama penceresinde aşağıdaki mesaj görünecektir: asind (0,5) = 30. istenilen açının değeri 30 derecedir.
Kaynaklar:
- Bradis tabloları (sinüsler, kosinüsler)
Matematikte kosinüs teoremi çoğunlukla bir açının üçüncü tarafını ve iki tarafını bulmanın gerekli olduğu durumlarda kullanılır. Ancak bazen problemin durumu tam tersi olabilir: Verilen üç kenarla bir açı bulmanız gerekir.

Talimatlar
Size iki kenarının uzunluğu ve bir açısının değeri bilinen bir üçgen verildiğini hayal edin. Bu üçgenin tüm açıları birbirine eşit değildir ve kenarlarının boyutları da farklıdır. γ açısı, bu şeklin tabanı olan AB ile gösterilen üçgenin kenarının karşısında yer alır. Bu açının yanı sıra AC ve BC'nin geri kalan tarafları boyunca, kosinüs teoremini kullanarak üçgenin bilinmeyen tarafını bulabilir ve bundan aşağıda sunulan formülü elde edebilirsiniz:
a^2=b^2+c^2-2bc*cosγ, burada a=BC, b=AB, c=AC
Kosinüs teoremine genelleştirilmiş Pisagor teoremi denir.
Okumak faydalı olabilir:
- Kesişen çizgiler arasındaki açı - tanım, bulma örnekleri Kesişen çizgiler nasıl belirlenir;
- Çözümlü ve çözümsüz problem örnekleri;
- Biyolojide metabolizma ne anlama gelir?;
- Rubtsov'un eski yol şiirinin analizi Nikolay Rubtsov eski yol;
- Asonans: edebiyattaki örnekler;
- Çeşitli maddelerin elektriksel iletkenliği;
- Bölüm X İçin İnceleme Soruları 13. Bölüm İçin İnceleme Soruları;
- Metallerin fiziksel özellikleri - Bilgi Hipermarket IVB grubu metallerin fiziksel özellikleri;