Основні властивості подвійного інтегралу. Завдання подвійний інтеграл визначення основні властивості подвійного інтеграла Подвійний інтеграл основні поняття та визначення
Основні властивості подвійного інтегралу
Властивості подвійного інтеграла (та його висновок) аналогічні відповідним властивостям одноразового певного інтеграла.
1°. Адитивність. Якщо функція f(x, y) інтегрована в області Dі якщо область Dза допомогою кривої Гплощі нуль розбивається на дві зв'язкові та не мають загальних внутрішніх точок області D 1 і D 2 , то функція f(x, y) інтегрована в кожній з областей D 1 і D 2 , причому
2°. Лінійна властивість. Якщо функції f(x, y) та g(x, y) інтегровані в області D, а α і β - будь-які речові числа, то функція [ α · f(x, y) + β · g(x, y)] також інтегрована в області D, причому
3°. Якщо функції f(x, y) та g(x, y) інтегровані в області D, то і добуток цих функцій інтегрується в D.
4°. Якщо функції f(x, y) та g(x, y) обидві інтегровані в області Dі всюди в цій галузі f(x, y) ≤ g(x, y), то
5°. Якщо функція f(x, y) інтегрована в області D, те й функція | f(x, y)| інтегрована в області D, причому
(Звичайно, з інтегрованості | f(x, y)| в Dне випливає інтегрованість f(x, y) в D.)
6°. Теорема про середнє значення. Якщо обидві функції f(x, y) та g(x, y) інтегровані в області D, функція g(x, y) невід'ємна (непозитивна) всюди в цій галузі, Mі m- точна верхня та точна нижня грані функції f(x, y) в області D, то знайдеться число μ , що задовольняє нерівності m ≤ μ ≤ Mі таке, що справедлива формула
Завдання, що веде до поняття подвійного інтеграла Визначення подвійного інтеграла Основні властивості подвійного інтеграла Площа плоскої області Зведення подвійного інтеграла до повторного Заміна змінних у подвійному інтегралі Елемент площі в криволінійних координатах Якобіан та його геометричний зміст Формула заміни змінних в подвій


















Завдання, що веде до поняття подвійного інтеграла. Визначення подвійного інтегралу. До поняття подвійного інтеграла ми приходимо, вирішуючи конкретне завдання обчислення об'єму циліндричного тіла. Циліндричним тілом називається тіло, обмежене площиною хОу, деякою поверхнею та циліндричною поверхнею, що утворюють яку паралельні осі (див. рис.1). Область D зміни змінних х і у називається основою циліндричного тіла. При визначенні об'єму тіла виходитимемо з двох принципів: !) якщо розбити тіло на частини, то його об'єм дорівнює сумі об'ємів усіх частин (властивість адитивності); 2) обсяг прямого циліндра, обмеженого площиною z = const, паралельної площині хОу, дорівнює площі основи, помноженої на висоту. Надалі ми будемо припускати, що область D є зв'язною (що складається з одного шматка), квадрованою (тобто має площу) і обмеженою (тобто розташованою всередині деякого кола з центром на початку координат). Нехай - безперервна функція точки Р(х, у) в області скрізь в області Z>, тобто що циліндрична поверхня, що розглядається, цілком лежить над площиною хОу. Позначимо об'єм циліндричного тіла через V. Розіб'ємо область D - основу циліндричного тіла - на деяке число п квадрованих областей довільної форми, що не перетинаються; називатимемо їх частковими областями. Пронумерувавши часткові області у якомусь порядку, площі – через відповідно. Назвемо діаметром часткової області Dk величину Завдання, що призводить до поняття подвійного інтегралу інтеграл у полярних координатах де символ р(Р; Q) означає відстань між точками Р і Q. Позначимо через d найбільший діаметр часткових областей Dk (к = 1,2,..., п). Проведемо через кордон кожної часткової області циліндричну поверхню з утворюючими паралельними осі Oz. В результаті циліндричне тіло виявиться розбитим на п часткових циліндричних тіл. Замінимо яке часткове тіло прямим циліндром з тією ж основою і висотою, що дорівнює аплікату якої-небудь точки замінної поверхні (рис. 2). Об'єм такого циліндра дорівнює де точка – площа області Dk. Виконавши описані побудови для кожного часткового циліндричного тіла, отримаємо п-ступінчасте тіло, об'єм якого (про Інтуїтивно ясно, що Vn тим точніше висловлює об'єм V, що шукається, чим менше розміри часткових областей Dk. Приймаємо об'єм V циліндричного тіла рівним межі, якого прагне об'єм (1) п-ступінчастого тіла при n-юоі прагненні до нуля найбільшого діаметра d часткових областей Dk. Природно, межа ні залежати від виду розбиття області D на часткові області Dk і від вибору точок Рк у часткових областях. Нехай /(х, у) - довільна функція, задана в ділянці D. Сума п (1) називається інтегральною сумою для функції f(x)y) в ділянці D, що відповідає даному розбиття цієї області на п часткових областей і даному вибору точок Ж ®*,!/*) на часткових областях Dk. Визначення. Якщо при d -* існує межа інтегральних сум п не залежить ні від способу розбиття області D на часткові області, ні від вибору точок Рк в часткових областях, то він називається подвійним інтегралом від функції f(P) (або f(x, у )) по області D і позначається символом АБО Отже, (2) Самафункція f(x, у) при цьому називається інтегрованою в області D (f(P) - підінтегральна функція, f(P) dS - підінтегральний вираз, dS - диференціал ( або елемент) площі, область D - область інтегрування; .. Повертаючись до циліндричного тіла, укладаємо: обсяг циліндричного тіла, обмеженого площиною хОу, поверхнею, і циліндричною поверхнею з утворюючими, паралельними осі Ог, дорівнює подвійному інтегралу від функції /(х, у) по ділянці D, що є основою циліндричного тіла. / АБО Тут dx dy – елемент площі в декартових координатах. Такий геометричний зміст подвійного інтегралу від негативної функції. Якщо об'єм Якщо в області D функції f(P) приймає як позитивні, так і негативні значення, то інтеграл представляє суму алгебри об'ємів тих частин тіла, які розташовані над площиною хОу (беруться зі знаком «+»), і тих частин тіла, які розташовані під площиною хоу (беруться зі знаком «-»). До складання сум виду (1) для функції двох незалежних змінних і до наступного граничного переходу наводять найрізноманітніші задачі, а не тільки об'єм циліндричного тіла. Сформулюємо достатні умови інтегрованості. Теорема 1. Будь-яка функція у), безперервна в обмеженій замкнутій ділянці D, інтегрована в цій ділянці. Вимога безперервності підінтегральної функції часто виявляється занадто сором'язливим. Для додатків важлива наступна теорема, яка гарантує існування подвійного інтеграла деякого класу розривних функцій. Будемо говорити, що кілька точок площини, має площу нуль, якщо його можна укласти в багатокутну фігуру як завгодно малої площі. Теорема 2. Якщо функція /(ж, у) обмежена в замкнутій обмеженій області D і безперервна всюди D, крім деякого безлічі точок площі нуль, то ця функція інтегрована в області D. §2. Основні властивості подвійного інтеграла Подвійні інтеграли мають ряд властивостей, аналогічних властивостям певного інтеграла для функцій однієї незалежної змінної. 2.1. Лінійна властивість Якщо функції інтегруються в області D, а а і р - будь-які речові числа, то функція af) також інтегрована в області D, причому о) 2.2. Інтегрування нерівностей Якщо функції інтегруються в області D і всюди в цій області то (2) тобто нерівності можна інтегрувати. Зокрема, інтегруючи очевидні нерівності отримаємо Площа плоскої області Площа плоскої області D дорівнює подвійному інтегралу по цій галузі від функції, тотожно рівної одиниці. Дійсно, інтегральна сума для функції /(Р) = 1 в області D має вигляд і при будь-якому розбиття області D на часткові області Dt, що дорівнює її площі S. Але тоді і межа цієї суми, тобто подвійний інтеграл, дорівнює площі S області D: або, що те саме, (3) 2.4. Оцінка інтеграла Нехай функція /(Р) безперервна в обмеженій замкнутій ділянці D, нехай М і тп - максимальне і найменше значення /(Р) в ділянці D і 5 - її площа. Тоді (4) 2.5. Адитивність: Якщо функція /(Р) інтегрована в області D і область Z) розбита на дві області D і Di без загальних внутрішніх точок, то / (Р) інтегрована на кожній з областей D і Di, причому (5) 2.6. Теорема про середнє значення Теорема 3 (про середнє значення). Якщо функція /(Р) безперервна в замкнутій обмеженій області D, то знайдеться принаймні одна точка Рс області D така, що буде справедлива формула і де S - площа області D Справді, оскільки /(Р) безперервна в замкнутій обмеженій області D області D, вона приймає в D своє найбільше значення М і своє найменше значення т. За властивістю 4 про оцінку інтеграла маємо Таким чином, число укладено між найбільшим і найменшим значеннями функції /(Р) в області D. В силу безперервності функції /( Р) в області D вона приймає в деякій точці Рс G D значення, що дорівнює цьому числу, звідки S Значення f(Pc), що визначається по формулі (7), називається середнім значенням функції f(P) в області D. Геометричний сенс теореми про середнє Якщо в області D функція /(Р) ^ О, то формула (6) означає, що існує прямий циліндр з основою D (площа якого дорівнює 5) і висотою Н = /(Рс), об'єм якого дорівнює об'єму циліндричного тіла (рис . 3). § 3. Зведення подвійного інтеграла до повторного Одним із ефективних способів обчислення подвійного інтеграла є зведення його до повторного. 3.1. Випадок прямокутника Нехай область D - замкнуте прямокутник П зі сторонами, паралельними осям координат. Нехай функція f(x, у) неперервна у прямокутнику П. Подвійний інтеграл можна інтерпретувати як (алгебраїчний) об'єм циліндричного тіла з основою П, обмеженого поверхнею. Розглянемо відповідне циліндричне тіло. Проведемо площину перпендикулярну до осі Оу (рис.4). Ця площина розсіче циліндричне тіло по криволінійній трапеції, обмеженій зверху плоскою лінією z, що описується рівняннями. ). Розмір інтеграла (1) залежить від вибору значення уо. Покладемо (2) Вираз (2) дає площу поперечного перерізу циліндричного тіла як функції від у. Тому об'єм циліндричного тіла можна обчислити за формулою. Визначення подвійного інтеграла Основні властивості подвійного інтеграла Площа плоскої області Зведення подвійного інтеграла до повторного Заміна змінних у подвійному інтегралі Елемент площі в криволінійних координатах Якобіан та його геометричний зміст Формула заміни змінних у подвійному інтегралі Подвійний інтеграл у такому знайти також за площами перерізів площинами х = х0. Це призводить до формули (4) Кожен із виразів, що стоять у правих частинах формул (3) і (4), містить дві послідовні операції звичайного інтегрування функції /(ж, у). Вони називаються повторними інтегралами від функції /(ж, у) по області П. Якщо /(ж, у) безперервна в замкнутому прямокутнику П, то перехід до повторних інтегралів завжди можливий і (5) тобто значення повторних інтегралів від безперервної функції /(А, у) не залежать від порядку інтегрування. Приклад 1. Знайти подвійний інтеграл від функції області Маємо (див. рис. 5): 3.2. Випадок довільної області Припустимо тепер, що областю інтегрування є довільна обмежена квадрована зам до нута я область D на площині хОу, що задовольняє наступній умові: будь-яка пряма, паралельна осі Оу, перетинає межу області D не більше ніж у двох точках або по цілому відрізок . 6 а). Укласти область D всередину прямокутника так, як показано на рис. 66. Відрізок [а, 6] є ортогональна проекція області D на вісь Оху а відрізок [с, dj - ортогональна проекція області D на вісь Оу. Точками А та С межа області D розбивається на дві криві ABC та АЕС. Кожна з цих кривих перетинається з довільною прямою, паралельною осі Оу, лише в одній точці. Тому їх рівняння можна записати у формі, дозволеній щодо у: Нехай f(x, у) - деяка функція, безперервна в ділянці D. Розсічемо розглянуте циліндричне тіло площиною. У перерізі отримаємо криволінійну трапецію PQMN (рис.7), площа якої виражається звичайним інтегралом від функції /(х, у), що розглядається як функція однієї змінної у. У цьому змінна у змінюється від ординати точки Р до ординати точки Q точка Р єто*!-ка «входу» прямий х = const (у площині) в область - точка її «виходу» з цієї області. Так як рівняння кривої ABC є, а кривою ці ординати при взятому х відповідно рівні. Отже, інтеграл дає нам вираз для площі плоского перерізу циліндричного тіла як функції положення площини січної х = const. Обсяг всього тіла дорівнюватиме інтегралу від цього виразу по ж у проміжку зміни. Таким чином, Зокрема, для площі S області D отримаємо Припустимо тепер, що кожна пряма перетинає межу області D не більше ніж у двох точках Р і Q, абсциси яких рівні відповідно (або по цілому відрізку) (рис. 8). Проводячи аналогічні міркування, приходимо до формули, що також зводить обчислення подвійного інтеграла до повторного. Приклад 2. Обчислити подвійний інтеграл від функції області D. обмеженою лініями ^ Перший спосіб. Зобразимо область інтегрування D. Пряма у = х парабола у = х2 перетинаються в точках). Значить, х змінюється 8 межах від 0 Будь-яка пряма х = const) перетинає межу області не більше ніж у двох точках. Тому може бути застосована формула (8): Другий спосіб (рис. 10). Застосовуючи формулу (10). отримаємо той же результат: Приклад 3. Обчислити об'єм тіла, обмеженого поверхнею перетинається з площиною хОу по лінії еліпс з півосями в силу симетрії даного тіла щодо координатних площин жОж і Ох отримуємо: Зауваження. Якщо область D така, що деякі прямі (осртекальні або горизонтальні) перетинають її межу більш ніж у двох точках, то для обчислення подвійного інтеграла по області D слід розбити її відповідним чином на частини, свссгм до повторних каяцій з інтегралів поетом частинам і отримані результати скласти . Приклад 4. Обчислити подвійний інтеграл області D, укладеної між двома квадратами з центрам і на початку координат і сторонами, паралельними осям координат, якщо сторона внутрішнього квадрата дорівнює 2, а зовнішнього - 4. безперервна як у великому квадраті Q, сторона якого дорівнює 4 , і у малому квадраті Р. сторона якого дорівнює 2 (рис. 12). Відповідно до теореми 1, інтеграли від функції е*** за зазначеними квадратами існують, отже величина шуканого інтеграла §4. Заміна змінних у подвійному інтегралі 4.1. Поняття криволінійних координат точки Нехай у ділянці D* площині uOv задана пара функцій які ми вважатимемо безперервними у цій галузі і мають безперервні приватні похідні. У силу рівняння (1) кожній точці М*(«, v) області D* відповідає одна певна точка М(х, у) у площині хОу і тим самим точкам області D* відповідає деяка множина D точок (ж, у) в площині хоу (рис. 13). При цьому говорять, що функції (1) здійснюють відображення області D4 на множину D. Припустимо, що різним точкам (u, v) відповідають різні точки (x, y). Це рівнозначно однозначної роздільності рівнянь (1) щодо u, v: У цьому випадку відображення називається взаємно однозначним відображенням області D* на область D. При такому перетворенні будь-яка безперервна крива L*, що лежить в області D*, перейде в безперервну криву L, що лежить в області D. Якщо функції д(х) у) та h(x, у) також безперервні, то будь-яка безперервна лінія LCD за допомогою перетворення (2) перейдете безперервну лінію L*C D*. По заданій парі Щ, Vo значень змінних і, v з області D * можна однозначно визначити не тільки положення крапки M * (u<)> Vq) у самій ділянці £)*, але і положення відповідної точки М(хо, уо) в ділянці D, хо = 4>(іо, v0), 3/0 = o,vo). Це дає підставу розглядати числа u, як деякі нові координати точки D області М на площині хОу. Їх називають криволінійними координатами точки М. Безліч точок області D, у яких одна з координат зберігає постійне значення, називають координатною лінією. Вважаючи у формулі (1) і = vq, отримаємо параметричні рівняння координатної лінії, Тут роль параметра грає змінна і. Надаючи координаті v різні (можливі нею) постійні значення, отримаємо сімейство координатних ліній (v = const) на площині хОу. Аналогічно отримуємо й іншу родину координатних ліній (і = const). За наявності взаємно однозначної відповідності між областями D* і D різні координатні лінії одного й того ж сімейства не перетинаються між собою, і через будь-яку точку області D проходить по одній лінії з кожної родини. Сітка криволінійних координатних ліній на площині хОр є образом прямокутної сітки на площині uOv (див. рис. 13). 4.2. Елемент площі у криволінійних координатах. Якобіан та його геометричний сенс Виділимо в області D* на площині Uo*V малий прямокутник P*P?P$Pl зі сторонами, паралельними осям координат 0*і та О” v та довжинами сторін Аі та Av (для визначеності вважаємо, що А ) відповідно (рис. 14 а), його площа Прямокутник переходить у криволінійний чотирикутник * у ділянці D (рис. 146). Користуючись формулою Тейлора для функції двох змінних і обмежуючись членами першого часу/рса щодо Аї і Av, отримаємо наступні наближені значення координат для вершин чотирикутника, де функції всі їх похідні обчислені в точці. порядку чотирикутник P\PiPiPa є паралелограм.То випливає з того, що тоді площа ДS чотирикутника можна приблизно виразити через довжину векторного твору, Завдання, що призводить до поняття подвійного інтеграла Визначення подвійного інтеграла Основні властивості подвійного інтеграла подвійний інтеграл Елемент площі в криволінійних координатах Якобіан і його геометричний зміст точці (tx, v)) при відображенні її на ділянку D за допомогою формул перетворення (1). 4.3. Формула заміни змінних у подвійному інтегралі Нехай безперервні функції здійснюють однозначне відображення області D* на D і мають безперервні приватні похідні першого порядку. Нехай в області D на площині хОу задана безперервна функція Кожному значенню функції в області D відповідає рівне значення функції г = в області D", де. Розіб'ємо область D * на часткові області і побудуємо відповідне розбиття області D. Виберемо у відповідних часткових областях точки (і, v) і (ж, у) так, щоб значення функцій у них збігалися, і складемо інтегральні суми для функцій z = / (ж, у) і v) по областях D і D *. рівності (9) до межі при прагненні до нуля найбільшого діаметра d* часткових областей D\ (через безперервність відображення (I) буде прагнути до нуля і найбільший з діаметрів d часткових областей у D), матимемо де Умову J Ф 0 є умовою локальної взаємнооднозначності відображення, що здійснюється функціями Теорема 4. Для того щоб перетворити подвійний інтеграл, заданий в декартових координатах, подвійний інтеграл в криволінійних координатах, потрібно замінити в підінтегральної функції /(ж, у) змінні ж і у відповідно через а елемент площі dx - Його виразом у криволінійних координатах: Приклад. Знайти площу фігури, обмеженої гіперболами м. Відшукання площі зазначеної фігури зводупся до обчислення подвійного інтеграла по області О. Введемо нові, криволінійні координати та й про формули З умови аадачі ясіо, що. Значить, у площині uOv ми отримали прямокутник (рис. 156) - фігуру простішу, ніж задана фігура D. Елемент площі в полярних координатах має вигляд і формулу переходу від інтеграла в декартових координатах до інтегралу в полярних координатах можна записати так: У цьому випадку (13) Елемент площі в полярних координатах можна отримати і із геометричних міркувань (див. рис. 16). Площа заштрихованої малюнку області А = пл. сектори. сектора Відкидаючи нескінченно малу величину вищого порядку, отримуємо та приймаємо за елемент площі у полярних координатах. Отже, щоб перетворити подвійний інтеграл в декартових координатах в подвійний інтеграл в полярних координатах, потрібно а: і у підінтегральної функції замінити відповідно через р costp і psiny, а елементплощі в декартових координатах dx dy замінити елементом площі в полярних координатах р dp dip. Займемося тепер обчисленням подвійного інтеграла у полярних координатах. Як і у разі прямокутних декартових координат, обчислення інтеграла в полярних координатах здійснюється шляхом зведення його до повторного інтегралу. Розглянемо спочатку випадок, коли полюс Про лежить поза заданою ділянкою D. Нехай область D має ту властивість, що будь-який промінь, що виходить з полюса (координатна лінія у перетинає її межу не більше ніж у двох точках або по цілому відрізку (рис. 17). Зазначимо крайні значення i полярного кута є межами зовнішнього інтегрування.Промінь ц> = проходить через точку А контуру області D, а промінь через точку В. Точки Aw розбивають контур області D на дві частини: АСВ і AFB.Нехай - їх полярні рівняння, причому) - однозначні безперервні функції, що задовольняють умові Функції є межами внутрішнього інтегрування. Переходячи до повторних інтегралів, отримуємо наступну формулу Зокрема, для площі S області D при F(p, г 1 отримуємо Пусть тепер полюс Про розташований всередині області D. Припустимо, що область D є зоряною щодо полюса, тобто будь-який промінь tp = const перетинає межу області тільки в одній точці або по целрму відрізку (мал. 18) Нехай - рівняння кордону області в полярних координатах. областю інтегрування буде прямокутник Перетворений інтеграл / легко обчислюється: г Примітка Якщо якобіан відмінний від нуля в області D, то відображення в деякій околиці кожної точки цієї області є взаємнооднозначним. Розглянемо відображення, яке визначається функціями Якобіан цих функцій дорівнює і, отже, скрізь відмінний від нуля. Незважаючи на це, ми отримаємо, так що це відображення не є взаємнооднозначним. З іншого боку, якщо якобіан відображення перетворюється на нуль у якій-небудь точці, то, проте, відображення в околиці цієї точки може виявитися взаємно однозначним. Наприклад, для відображення, що визначається функціями якобіан дорівнює нулю і при, але відображення є взаємнооднозначним. Зворотне відображення визначається функціями
1.1 Визначення подвійного інтегралу





1.2 Властивості подвійного інтегралу
Властивості подвійного інтеграла (та його висновок) аналогічні відповідним властивостям одноразового певного інтеграла.
1°. Адитивність. Якщо функція f(x, y) інтегрована в області D і якщо область D за допомогою кривої Г площі нуль розбивається на дві зв'язкові і не мають спільних внутрішніх точок області D 1 і D 2 , то функція f(x, y) інтегрована в кожній з областей D 1 і D 2 , причому
2 °. Лінійна властивість. Якщо функції f(x, y) та g(x, y) інтегруються в ділянці D, а? і? - будь-які речові числа, то функція [? · f (x, y) + ? · g (x, y)] також інтегрована в області D, причому
3 °. Якщо функції f(x, y) та g(x, y) інтегруються в області D, то і добуток цих функцій інтегрується в D.
4 °. Якщо функції f(x, y) і g(x, y) обидві інтегруються в області D і скрізь у цій галузі f(x, y)? g(x, y), то
5 °. Якщо функція f(x, y) інтегрована області D, то й функція |f(x, y)| інтегрована в області D, причому
(Звичайно, з інтегрованості | f (x, y) | D не випливає інтегрованість f (x, y) в D.)
6 °. Теорема про середнє значення. Якщо обидві функції f(x, y) і g(x, y) інтегруються в області D, функція g(x, y) невід'ємна (непозитивна) усюди в цій галузі, M і m - точна верхня та точна нижня грані функції f( x, y) в області D, то знайдеться число?, Що задовольняє нерівність m? ? ? M і таке, що справедлива формула
Зокрема, якщо функція f(x, y) безперервна D, а область D зв'язкова, то в цій області знайдеться така точка (?, ?), Що? = f(?, ?), і формула набуває вигляду
7 °. Важлива геометрична властивість. дорівнює площі області D
Нехай у просторі дано тіло T (рис. 2.1), обмежене знизу областю D , зверху - графіком безперервної та невід'ємної функції) z = f (x, y ,) яка визначена в ділянці D , з боків - циліндричною поверхнею, спрямовуючою якої є межа області D, а утворюють паралельні осі Оz. Тіло такого виду називається циліндричним тілом.
1.3 Геометрична інтерпретація подвійного інтегралу





1.4 Поняття подвійного інтеграла прямокутника
Нехай довільна функція f(x, y) визначена всюди прямокутнику R = ? (див. рис. 1).

Розіб'ємо сегмент a? x? b на n часткових сегментів за допомогою точок a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.
Цьому розбиття за допомогою прямих, паралельних осях Ox і Oy відповідає розбиття прямокутника R на n · p часткових прямокутників R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Вказане розбиття прямокутника R позначимо символом T. Надалі у цьому розділі під терміном "прямокутник" розумітимемо прямокутник зі сторонами, паралельними координатним осям.
На кожному частковому прямокутнику Rkl виберемо довільну точку (?k,?l). Поклавши ?x k = x k - x k-1, ?y l = y l - y l-1, позначимо через ?R kl площа прямокутника R kl . Вочевидь, ?R kl = ?x k ?y l .
називається інтегральною сумою функції f(x, y), що відповідає даному розбиття T прямокутника R і даному вибору проміжних точок (? k , l) на часткових прямокутниках розбиття T.
Діагональ називатимемо діаметром прямокутника R kl . Символом? позначимо найбільший із діаметрів всіх часткових прямокутників R kl .
Число I називається межею інтегральних сум (1) при? > 0, якщо будь-якого позитивного числа? можна вказати таке позитивне число? що при?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство
| ? - I |< ?.
Функція f(x, y) називається інтегрованою (за Ріманом) на прямокутнику R, якщо існує кінцева межа I інтегральних сум цієї функції при? >0.
Вказана межа I називається подвійним інтегралом від функції f(x, y) по прямокутнику R і позначається одним із наступних символів:
Зауваження. Так само, як і для одноразового певного інтеграла, встановлюється, що будь-яка інтегрована на прямокутнику R функція f(x, y) є обмеженою на цьому прямокутнику.
Це дає підставу розглядати надалі лише обмежені функції f(x, y).
Завдання, що веде до поняття подвійного інтеграла.
Припустимо, що на визначено функцію елементів ![]() і запишемо суму
і запишемо суму

яка називається інтегральною.
В: Під певним інтегралом (о.і.) від функції та від вибору ![]()
Позначення: 
Числа називають інтегрованою (за Ріманом) на .
Т. існування: За умови, що .
Відповідно до визначення о.і. зазначимо, що інтеграл має залежність від виду , меж і , проте залежить від символу позначення змінної , інакше висловлюючись

Відповідно до п.17.1.1 та 17.1.2 та визначення о.і. запишемо формули площі криволінійної трапеції:  , роботи сили
, роботи сили ![]()
на: 
Поняття подвійного інтеграла, інтегральних сум.
Існування подвійного інтеграла, тобто межі інтегральної суми для здається очевидним, так як ця межа дає об'єм циліндричного тіла. Однак це міркування не є суворим. У повніших курсах це твердження суворо доводиться і зветься теореми існування подвійного інтеграла.

Теорема існування. Для будь-якої функції, безперервної в обмеженій замкнутій області, що має площу а, існує подвійний інтеграл, тобто існує межа інтегральних сум при необмеженому збільшенні числа малих майданчиків за умови, що кожен з них стягується в крапку. Ця межа не залежить ні від способу розбиття області, а на частині ні від вибору точок.
Надалі ми розглядатимемо лише функції, безперервні у сфері інтегрування.
З теореми існування випливає, що ми можемо, наприклад, розбити область на малі прямокутники зі сторонами прямими, паралельними осям координат (рис. 230). При цьому. Вибираючи потім у кожному малому прямокутнику по точці ми можемо написати, згідно з визначенням подвійного інтеграла
Щоб підкреслити, що подвійний інтеграл можна одержати як межа суми виду замість позначення використовують також позначення
Вираз називається елементом площі в декартових координатах і дорівнює площі прямокутника зі сторонами паралельними координатним осям.
Зауважимо, що при складанні інтегральної суми майданчики, що прилягають до межі області а, не мають форми прямокутників. Однак можна довести, що помилка від заміни таких майданчиків прямокутниками з площами межі зведеться до нуля.
Властивості подвійних інтегралів
Властивості подвійного інтеграла (та його висновок) аналогічні відповідним властивостям одноразового певного інтеграла.
1°. Адитивність. Якщо функція f(x, y) інтегрована в області Dі якщо область Dза допомогою кривої Гплощі нуль розбивається на дві зв'язкові та не мають загальних внутрішніх точок області D 1 і D 2 , то функція f(x, y) інтегрована в кожній з областей D 1 і D 2 , причому
2°. Лінійна властивість. Якщо функції f(x, y) та g(x, y) інтегровані в області D, а α і β - будь-які речові числа, то функція [ α · f(x, y) + β · g(x, y)] також інтегрована в області D, причому
![]()
![]()
3°. Якщо функції f(x, y) та g(x, y) інтегровані в області D, то і добуток цих функцій інтегрується в D.
4°. Якщо функції f(x, y) та g(x, y) обидві інтегровані в області Dі всюди в цій галузі f(x, y) ≤ g(x, y), то
5°. Якщо функція f(x, y) інтегрована в області D, те й функція | f(x, y)| інтегрована в області D, причому
(Звичайно, з інтегрованості | f(x, y)| в Dне випливає інтегрованість f(x, y) в D.)
6°. Теорема про середнє значення. Якщо обидві функції f(x, y) та g(x, y) інтегровані в області D, функція g(x, y) невід'ємна (непозитивна) всюди в цій галузі, Mі m- точна верхня та точна нижня грані функції f(x, y) в області D, то знайдеться число μ , що задовольняє нерівності m ≤ μ ≤ Mі таке, що справедлива формула
Зокрема, якщо функція f(x, y) безперервна в D, а область D зв'язкова, то в цій галузі знайдеться така точка ( ξ , η ), що μ = f(ξ , η ), і формула (11) набуває вигляду
Для функції двох змінних, заданої як z = f(x, y) .
Записується подвійний інтеграл так:
Тут D- Плоска фігура, обмежена лініями, вирази яких (рівності) дано в заданні обчислення подвійного інтеграла. Зліва та справа – рівностями, в яких зліва змінна x, а зверху та знизу – рівностями, у яких ліворуч змінна y. Це і далі – одне з найважливіших розуміння техніки обчислення подвійного інтеграла.
Обчислити подвійний інтеграл - означає знайти число, що дорівнює площі згаданої фігури D .
Поки що ми не торкаємося визначення подвійного інтегралу , а вчитимемося його обчислювати. Зрозуміти, що таке подвійний інтеграл, простіше, коли вирішено кілька завдань з його обчислення, тому визначення подвійного інтеграла ви знайдете наприкінці цього уроку. Ледве забігаючи вперед, можна лише відзначити, що визначення подвійного інтеграла також пов'язане зі згадуваною фігурою D .
Якщо фігура Dє прямокутник, всі лінії, що обмежують її - це прямі лінії. Якщо фігура D- криволінійна, то ліворуч і праворуч вона обмежена прямими, а згори і знизу – кривими лініями, заданими рівностями, які в задании. Бувають і випадки, коли постать D– трикутник, але про такі випадки трохи далі.
Для обчислення подвійного інтеграла потрібно таким чином розсортувати лінії, що обмежують фігуру D, Що має сувора назва - область інтегрування. Розсортувати на ліві та праві та на верхні та нижні. Це буде потрібно при зведення подвійного інтеграла до повторного інтегралу – метод обчислення подвійного інтеграла.
Випадок прямокутної області:

Випадок криволінійної області:

А це вже рішення знайомих нам певних інтегралів, у яких задані верхня та нижня межі інтегрування. Вирази, що задають лінії, які обмежують фігуру D, будуть межами інтегрування для звичайних певних інтегралів, яких ми вже підходимо.
Зведення подвійного інтеграла до повторного
Випадок прямокутної області
Нехай для такої функції існує подвійний інтеграл
Щоб обчислити цей подвійний інтеграл , потрібно звести його до повторного інтегралу, який має вигляд
![]() .
.
Спочатку потрібно обчислювати внутрішній (правий) певний інтеграл, потім – зовнішній (лівий) певний інтеграл.
Можна і поміняти ролями xі y
![]() .
.
приклад 1.Обчислити подвійний інтеграл

Обчислюємо внутрішній (правий) інтеграл, вважаючи гравець константою. Отримуємо.
 .
.

приклад 2.Обчислити подвійний інтеграл
![]() ,
,
Рішення. Зводимо цей подвійний інтеграл до повторного інтегралу
На кресленні будуємо область інтегрування:


Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого щойно внутрішнього (правого):
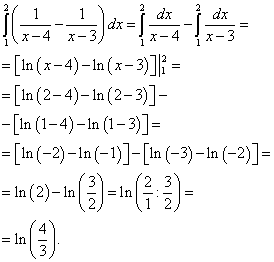
Результат і буде рішенням цього подвійного інтегралу.
Обчислити подвійний інтеграл самостійно, а потім переглянути рішення
Випадок криволінійної чи трикутної області
Нехай знову дана функція двох змінних f(x, y) , а обмеження для D: вже трохи іншого виду:
Цей запис означає, що фігуру Dліворуч і праворуч обмежують, як і у випадку прямолінійної області - прямі x = aі x = b, але знизу та зверху - криві, які задані рівняннями та . Іншими словами, і – функції.
Нехай для такої функції також існує подвійний інтеграл
Щоб обчислити цей подвійний інтеграл, потрібно звести його до повторного інтеграла, який має вигляд
 .
.
Тут межі інтегрування aі b- Числа, а і - функції. У разі трикутної області одна з функцій або – це рівняння прямої лінії. Такий випадок буде розібрано на прикладі 3.
Як і у випадку прямолінійної області, спочатку потрібно обчислювати правий інтеграл, потім - лівий певний інтеграл.
Так само можна поміняти ролями xі y. Тоді повторний інтеграл матиме вигляд
 .
.
Такий повторний інтеграл потрібно вирішувати так само: спочатку - внутрішній (правий) інтеграл, потім - зовнішній (лівий).
Приклад 5.Обчислити подвійний інтеграл
![]() ,
,
Рішення. Зводимо цей подвійний інтеграл до повторного інтегралу
![]() .
.
На кресленні будуємо область інтегрування і бачимо, що вона трикутна:

Обчислюємо внутрішній (правий) інтеграл, вважаючи ікс константою. Отримуємо.

Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого щойно внутрішнього (правого). Спочатку представляємо цей інтеграл у вигляді суми інтегралів:
![]() .
.
Обчислюємо перший доданок:

Обчислюємо другий доданок:

Обчислюємо третій доданок:

Отримуємо суму, яка буде рішенням даного подвійного інтеграла:
![]() .
.
Приклад 6.Обчислити подвійний інтеграл
Рішення. Зводимо цей подвійний інтеграл до повторного інтегралу
На кресленні будуємо область інтегрування:

Обчислюємо внутрішній (правий) інтеграл, вважаючи ікс константою. Отримуємо.
 .
.
Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого щойно внутрішнього (правого):

Результат і буде рішенням цього подвійного інтегралу.
x-правильна та неправильна, y-правильна та неправильна області інтегрування
Трапляється, що область інтегрування подвійного інтеграла обмежена такими лініями, що виникає необхідність розбити область інтегрування на частини та вирішувати кожен відповідний повторний інтеграл окремо. Це випадки, коли:
1) область інтегрування є фігурою, що має у вигляді нижньої або верхньої (лівої або правої) межі дві або більше двох прямих або кривих ліній;
2) область інтегрування є фігурою, межу якої прямі перетинають більш ніж у двох точках.
Якщо вищесказане відноситься до лівого або правого кордону області інтегрування, тобто обмеження, заданих лініями, вираженими через x, то область інтегрування називається x-Неправильною. Якщо ж пряма y = y0 перетинає відповідну межу лише в одній точці і якщо кордоном служить лише одна пряма чи крива, то область інтегрування називається x-правильною
Аналогічно, якщо кордон, заданий лініями, вираженими через yпряма x = x0 перетинає більш ніж в одній точці або якщо кордоном служать більш ніж одна пряма або крива, то область інтегрування називається y-Неправильною. Вивести тепер ознаки y-правильної області, мабуть, дуже просто.
Досі ми розглядали приклади з x-неправильними та y-Правильними областями інтегрування. Тепер розглянемо випадки, коли умова правильності порушується.
Приклад 7.Обчислити подвійний інтеграл, область інтегрування якого обмежена лініями y = x , xy = 1 , y = 2 .

Рішення. Область інтегрування є y-Неправильною, так як її нижню межу не можна задати однією лінією y = y(x) . Як видно на малюнку вище, нижня межа складається з y = x(темно-бордова) та xy= 1 (зелена). Тому прямий x= 1 (чорна) можемо розбити область інтегрування на частини - і .
Обчислюється цей подвійний інтеграл так:

Зміна порядку інтегрування
Як зазначалося вище, після приведення подвійного інтеграла до повторного інтегралу, можна поміняти змінні xі yролями, чи, інакше кажучи, змінити порядок інтегрування.
Зміна порядку інтегрування образно може бути описана наступними словами О "Генрі: "Так поводиться житель джунглів - звір, потрапивши в клітину, і так поводиться житель клітини - людина, заблукавши в джунглях сумнівів ". Результат, так само по О"Генрі один і той же: "Чалмерс розірвав листа на тисячу дрібних клаптиків і почав терзати свій дорогий килим, ходячи по ньому туди й сюди". ( Про "Генрі. Шехерезада з Медісон-скверу.)
Тоді, якщо лівий інтеграл у нас за змінною x, а правий - за y, То після зміни порядку інтегрування все буде навпаки. Тоді межі інтегрування для "нового" ігрека потрібно "запозичити" у "старого" ікса, а межі інтегрування для "нового" ікса отримати у вигляді зворотної функції, Дозволивши щодо ікса рівняння, що задавало межу для грека.
Приклад 8.
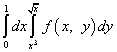 .
.
Рішення. Після зміни порядку інтегрування інтеграл за гріком стане лівим, а інтеграл за іксом - правим. Межі інтегрування для "нового" грека запозичимо у "старого" ікса, тобто нижня межа дорівнює нулю, а верхня - одиниці. Межі інтегрування для "старого" гравця задані рівняннями та . Дозволивши ці рівняння щодо ікса, отримаємо нові межі інтегрування для ікса:
(нижній) та (верхній).
Таким чином, після зміни порядку інтегрування повторний інтеграл запишеться так:
 .
.
Після зміни порядку інтегрування в подвійному інтегралі нерідко область інтегрування перетворюється на y-неправильну або x-Неправильну (див. попередній параграф). Тоді потрібно розбити область інтегрування на частини та вирішувати кожен відповідний повторний інтеграл окремо.
Оскільки розбиття області інтегрування на частини є певними труднощами для багатьох студентів, то не обмежимося прикладом, наведеним у попередньому параграфі, а розберемо ще кілька прикладів.
Приклад 9.Змінити порядок інтегрування для повторного інтегралу
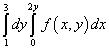 .
.
Рішення. Отже, область інтегрування даного повторного інтеграла обмежена прямими y = 1 , y = 3 , x = 0 , x = 2y .
При інтегруванні в іншому порядку нижня межа області складається із двох прямих: ABі BC, які задані рівняннями y= 1 і y = x/2 що видно на малюнку нижче.

Вихід із такої невизначеності полягає у розбитті області інтегрування на дві частини. Ділити область інтегрування буде пряма BМ. Нові межі інтегрування обчислюємо, знаходячи зворотну функцію. Відповідно до цього рішення повторний інтеграл після зміни порядку інтегрування дорівнюватиме сумі двох інтегралів:

Природно, таким самим буде рішення подвійного інтеграла, який зводиться до повторного інтеграла, даного за умови цього прикладу.
приклад 10.Змінити порядок інтегрування для повторного інтегралу
 .
.
Рішення. Отже, область інтегрування повторного інтеграла обмежена прямими x = 0 , x= 2 і кривими та .
Як видно на малюнку нижче, пряма, паралельна осі 0x, перетинатиме нижню межу області інтегрування більш ніж у двох точках.

Тому розіб'ємо область інтегрування на три частини прямими, які на малюнку накреслені чорним. Нові межі інтегрування обчислюємо, знаходячи зворотну функцію. Межі для трьох нових областей інтегрування будуть наступними.


Відповідно до цього рішення повторний інтеграл після зміни порядку інтегрування буде рівним сумі трьох інтегралів:

Тієї ж сумі трьох інтегралів дорівнюватиме і подвійний інтеграл, який зводиться до повторного інтегралу, даного за умови цього прикладу.
І все ж таки обставини непереборної сили нерідко заважають студентам вже на попередньому кроці - розстановці меж інтегрування. Тривога і сум'яття не позбавлені певної підстави: якщо для розбиття області інтегрування на частини зазвичай достатньо придивитися до креслення, а для вирішення повторного інтеграла - таблиці інтегралів, то в розташуванні меж інтегрування потрібен певний досвід тренувань. Пробіжимо приклад, в якому зупинимося тільки на розстановці меж інтегрування і – майже на автоматі – на розбиття області та опустимо саме рішення.
Приклад 11.Знайти межі інтегрування подвійного інтеграла, якщо область інтегрування Dзадана наступним чином:
y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.
Рішення. У явному вигляді (через xі y"без домішок") лінії, що обмежують область інтегрування, не задано. Так як для ікса ними найчастіше виявляються прямі, що стосуються в одній точці верхньої та нижньої меж, виражених через ігрек, то підемо саме цим шляхом. Тим більше що при зміні порядку інтегування ми отримаємо область інтегрування з такою самою площею. Дозволимо нерівності щодо гравця та отримаємо:
y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.
Будуємо отримані лінії на кресленні. Межами інтегрування з ікса справді служать лінії x= 0 і x= 2. Але область інтегрування виявилася y-Неправильною, так як її верхню межу не можна задати однією лінією y = y(x) .
Можливо, буде корисно почитати:
- ЖИТТЯ-БИЗ: смачна страва та відео в новому форматі Приступаємо до готування;
- Привіт з дитинства: печемо сметанні коржики Сметані коржі без дріжджів у духовці;
- Пісний шоколадний пиріг;
- Печиво «Ведмедики» з мигдалем;
- Салат з крабовими паличками та сиром Крабовий салат із сиром та яйцями;
- Котлети у фользі в духовці: рецепт, поради щодо приготування;
- Як зробити відворот за допомогою руни;
- До чого сниться сіль: знаки та символи уві сні;