ორმაგი ინტეგრალის ძირითადი თვისებები. ორმაგი ინტეგრალური პრობლემის განსაზღვრა ორმაგი ინტეგრალის ძირითადი თვისებები ორმაგი ინტეგრალური ძირითადი ცნებები და განმარტებები

ორმაგი ინტეგრალის ძირითადი თვისებები

ორმაგი ინტეგრალის თვისებები (და მათი წარმოშობა) მსგავსია ერთი განსაზღვრული ინტეგრალის შესაბამისი თვისებების.

1°. ადიტიურობა. თუ ფუნქცია ვ(x, წ) ინტეგრირებადია დომენში დდა თუ ტერიტორია დმრუდის გამოყენებით გფართობი ნული იყოფა ორ დაკავშირებულ რეგიონად, რომლებსაც არ აქვთ საერთო შიდა წერტილები დ 1 და დ 2, შემდეგ ფუნქცია ვ(x, წ) ინტეგრირებადია თითოეულ დომენში დ 1 და დ 2 და

2°. ხაზოვანი თვისება. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, ა α და β - ნებისმიერი რეალური რიცხვი, შემდეგ ფუნქცია [ α · ვ(x, წ) + β · გ(x, წ)] ასევე ინტეგრირებადია დომენში დ, და

3°. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, მაშინ ამ ფუნქციების პროდუქტი ინტეგრირებულია დ.

4°. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ორივე დომენის ინტეგრირებადია დდა ყველგან ამ მხარეში ვ(x, წ) ≤ გ(x, წ), ეს

5°. თუ ფუნქცია ვ(x, წ) ინტეგრირებადია დომენში დ, შემდეგ ფუნქცია | ვ(x, წ)| ინტეგრირებადი სფეროებში დ, და

(რა თქმა უნდა, ინტეგრაციიდან | ვ(x, წ)| ვ დინტეგრირება არ მოჰყვება ვ(x, წ) ვ დ.)

6°. საშუალო მნიშვნელობის თეორემა. თუ ორივე ფუნქციონირებს ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, ფუნქცია გ(x, წ) არის არაუარყოფითი (არაპოზიტიური) ყველგან ამ რეგიონში, მდა მ- ფუნქციის ზუსტი ზედა და ზუსტი ქვედა საზღვრები ვ(x, წ) ტერიტორიაზე დ, მაშინ არის ნომერი μ , უთანასწორობის დაკმაყოფილება მ ≤ μ ≤ მდა ისეთი, რომ ფორმულა მოქმედებს

ორმაგი ინტეგრალის კონცეფციამდე მიმავალი პრობლემა ორმაგი ინტეგრალის განსაზღვრა ბრტყელი რეგიონის ორმაგი ინტეგრალური ფართობის ძირითადი თვისებები ორმაგი ინტეგრალის შემცირება განმეორებით ინტეგრალამდე ცვლადების ცვლილება ორმაგ ინტეგრალურ ფართობის ელემენტში მრუდი კოორდინატებში იაკობიანი და მისი გეომეტრიული მნიშვნელობა ცვლადების ცვლილების ფორმულა ორმაგ ინტეგრალში ორმაგი ინტეგრალი პოლარულ კოორდინატებში

ორმაგი ინტეგრალის ცნებამდე მიმავალი პრობლემა. ორმაგი ინტეგრალის განმარტება. ორმაგი ინტეგრალის ცნებამდე მივდივართ ცილინდრული სხეულის მოცულობის გამოთვლის კონკრეტული პრობლემის გადაჭრით. ცილინდრული სხეული არის xOy სიბრტყით შემოსაზღვრული სხეული, გარკვეული ზედაპირი და ცილინდრული ზედაპირი, რომლის გენერატრიკები ღერძის პარალელურია (იხ. სურ. 1). x და y ცვლადების ცვლილების D რეგიონს ცილინდრული სხეულის ფუძე ეწოდება. სხეულის მოცულობის დადგენისას გამოვალთ ორი პრინციპიდან: !) თუ სხეულს დავყოფთ ნაწილებად, მაშინ მისი მოცულობა უდრის ყველა ნაწილის მოცულობის ჯამს (დანამატიურობის თვისება); 2) სწორი ცილინდრის მოცულობა, რომელიც შემოსაზღვრულია თვითმფრინავით z = const, xOy სიბრტყის პარალელურად, უდრის ფუძის ფართობს გამრავლებული სიმაღლეზე. შემდეგში ვივარაუდებთ, რომ რეგიონი D არის დაკავშირებული (შედგება ერთი ნაწილისგან), კვადრატულია (ანუ აქვს ფართობი) და შემოსაზღვრული (ანუ მდებარეობს საწყისზე ორიენტირებული გარკვეული წრის შიგნით). დავუშვათ P(x, y) წერტილის უწყვეტი ფუნქცია რეგიონში ყველგან Z> რეგიონში, ანუ განხილული ცილინდრული ზედაპირი მთლიანად xOy სიბრტყის ზემოთ დევს. ცილინდრული სხეულის მოცულობა ავღნიშნოთ V-ით. D რეგიონს - ცილინდრული სხეულის ფუძეს - ვყოფთ n-ზე გადამკვეთი ოთხკუთხედი თვითნებური ფორმის უბნებზე; ჩვენ მათ დავარქმევთ ნაწილობრივ რეგიონებს. ნაწილობრივი უბნების გარკვეული თანმიმდევრობით დანომრვის შემდეგ, არეები - შესაბამისად. მოდით ვუწოდოთ ნაწილობრივი რეგიონის დიამეტრს Dk რაოდენობა. პრობლემა, რომელიც იწვევს ორმაგი ინტეგრალის კონცეფციას. ცვლადები ორმაგ ინტეგრალში ფართობის ელემენტი მრუდი კოორდინატებში იაკობიანი და მისი გეომეტრიული მნიშვნელობა ცვლადების შეცვლის ფორმულა ორმაგ ინტეგრალში ორმაგი ინტეგრალი პოლარულ კოორდინატებში, სადაც სიმბოლო p(P; Q) ნიშნავს მანძილს P და Q წერტილებს შორის. მოდით აღვნიშნოთ d-ით ყველაზე დიდი ნაწილობრივი რეგიონების დიამეტრებიდან Dk (k = 1,2,..., n). მოდით დავხატოთ თითოეული ნაწილობრივი რეგიონის საზღვრიდან ცილინდრული ზედაპირი ოზის ღერძის პარალელურად გენერატორებით. შედეგად, ცილინდრული სხეული დაიყოფა n ნაწილობრივ ცილინდრულ სხეულად. მოდით შევცვალოთ ეს ნაწილობრივი სხეული სწორი ცილინდრით იგივე ფუძით და სიმაღლით, რომელიც ტოლია შეცვლილი ზედაპირის რომელიმე წერტილის აპლიკაციისა (ნახ. 2). ასეთი ცილინდრის მოცულობა უდრის იქ, სადაც წერტილი არის რეგიონის ფართობი Dk. თითოეული ნაწილობრივი ცილინდრული სხეულისთვის აღწერილი კონსტრუქციების განხორციელების შემდეგ, ჩვენ ვიღებთ n-საფეხურიან სხეულს, რომლის მოცულობა (o) ინტუიციურად, ცხადია, რომ Vn უფრო ზუსტად გამოხატავს სასურველ მოცულობას V, რაც უფრო მცირეა ნაწილობრივი რეგიონების ზომა. დკ. ჩვენ ვიღებთ ცილინდრული სხეულის V მოცულობას ტოლი ზღვრისა, რომლისკენაც n-საფეხურიანი სხეულის მოცულობა (1) მიდრეკილია როგორც n-ათასი, ხოლო ნაწილობრივი რეგიონების უდიდესი დიამეტრი d Dk ნულისკენ მიისწრაფვის. ბუნებრივია, ლიმიტი არ უნდა იყოს დამოკიდებული D რეგიონის დაყოფის ტიპზე Dk ნაწილებად და Pk წერტილების არჩევანზე ნაწილობრივ რეგიონებში. მოდით /(x, y) იყოს D დომენში განსაზღვრული თვითნებური ფუნქცია. n (1) ჯამს ეწოდება f(x)y ფუნქციის ინტეგრალური ჯამი D დომენზე, რომელიც შეესაბამება ამ დომენის მოცემულ დანაყოფს. n ნაწილობრივ დომენად და პუნქტების მოცემული არჩევანი Ж ®*,!/*) ნაწილობრივ დომენებზე Dk. განმარტება. თუ d -* 0-სთვის არის n ინტეგრალური ჯამების ზღვარი, რომელიც არ არის დამოკიდებული არც D დომენის ნაწილობრივ დომენებად დაყოფის მეთოდზე და არც Pk წერტილების არჩევაზე ნაწილობრივ დომენებში, მაშინ მას ეწოდება ორმაგი ინტეგრალი. ფუნქცია f(P) (ან f(x, y )) D დომენზე და აღინიშნება სიმბოლო OR ასე რომ, (2) თავად ფუნქციას f(x, y) ეწოდება ინტეგრირებადი D დომენში (f( P) არის ინტეგრანდი, f(P) dS არის ინტეგრანდ, dS არის ფართობის დიფერენციალური (ან ელემენტი), რეგიონი D - ინტეგრაციის რეგიონი; წერტილი P(®, y) - ინტეგრაციის ცვლადი სიზუსტე). ,.. ცილინდრულ სხეულს რომ დავუბრუნდეთ, დავასკვნით: xOy სიბრტყით შემოსაზღვრული ცილინდრული სხეულის მოცულობა, ზედაპირი და ცილინდრული ზედაპირი ოზის ღერძის პარალელურად გენერატრიციით, უდრის ფუნქციის ორმაგ ინტეგრალს /( x, y) D რეგიონზე, რომელიც არის ცილინდრული სხეულის ფუძე. / ან აქ dx dy არის ფართობის ელემენტი დეკარტის კოორდინატებში. ეს არის არაუარყოფითი ფუნქციის ორმაგი ინტეგრალის გეომეტრიული მნიშვნელობა. თუ მაშინ მოცულობა, თუ f(P) ფუნქციის D რეგიონში იღებს დადებით და უარყოფით მნიშვნელობებს, მაშინ ინტეგრალი წარმოადგენს სხეულის იმ ნაწილების მოცულობების ალგებრულ ჯამს, რომლებიც მდებარეობს xOy სიბრტყის ზემოთ (აღებული "+" ნიშანი) და სხეულის ის ნაწილები, რომლებიც მდებარეობს xOy სიბრტყის ქვეშ (აღებულია "-" ნიშნით). პრობლემების მრავალფეროვნება, და არა მხოლოდ ცილინდრული სხეულის მოცულობის პრობლემა, იწვევს ფორმის (1) ჯამების შედგენას ორი დამოუკიდებელი ცვლადის ფუნქციისთვის და შემდგომ გადასასვლელამდე ზღვრამდე. მოდით ჩამოვაყალიბოთ ინტეგრირებისთვის საკმარისი პირობები. თეორემა 1. ნებისმიერი ფუნქცია y) უწყვეტი შეზღუდულ დახურულ დომენში D არის ინტეგრირებადი ამ დომენში. ინტეგრანტის უწყვეტობის მოთხოვნა ხშირად ზედმეტად შემზღუდველი აღმოჩნდება. აპლიკაციებისთვის მნიშვნელოვანია შემდეგი თეორემა, რომელიც უზრუნველყოფს ორმაგი ინტეგრალის არსებობას გარკვეული კლასის უწყვეტი ფუნქციებისთვის. ჩვენ ვიტყვით, რომ სიბრტყეზე წერტილების გარკვეულ კომპლექტს აქვს ნულოვანი ფართობი, თუ ის შეიძლება იყოს ჩასმული თვითნებურად მცირე ფართობის მრავალკუთხა ფიგურაში. თეორემა 2. თუ ფუნქცია /(x, y) შემოსაზღვრულია დახურულ შემოსაზღვრულ D დომენში და უწყვეტია ყველგან D-ში, გარდა ნულის ფართობის წერტილების ზოგიერთი სიმრავლისა, მაშინ ეს ფუნქცია ინტეგრირებადია D დომენში. §2. ორმაგი ინტეგრალის ძირითადი თვისებები ორმაგი ინტეგრალებს აქვთ მთელი რიგი თვისებები, რომლებიც მსგავსია განსაზღვრული ინტეგრალის თვისებების ერთი დამოუკიდებელი ცვლადის ფუნქციებისთვის. 2.1. წრფივი თვისება თუ ფუნქციები) ინტეგრირებადია D დომენში, ხოლო a და p არის ნებისმიერი რეალური რიცხვი, მაშინ ფუნქცია af) ასევე ინტეგრირებადია D დომენში და o) 2.2. უტოლობების ინტეგრაცია თუ ფუნქციები ინტეგრირებადია D დომენში და ყველგან ამ დომენში, მაშინ (2) ანუ უტოლობები შეიძლება იყოს ინტეგრირებული. კერძოდ, აშკარა უტოლობების ინტეგრირებით ვიღებთ ბრტყელი რეგიონის ფართობი ბრტყელი რეგიონის ფართობი D უდრის ორმაგ ინტეგრალს ფუნქციის იდენტურად უდრის ერთიანობას. მართლაც, ინტეგრალურ ჯამს /(P) = 1 ფუნქციისთვის D დომენში აქვს ფორმა და Dt დომენის ნებისმიერი დაყოფისთვის ნაწილობრივ დომენებად Dt უდრის მის ფართობს S. მაგრამ მაშინ ამ ჯამის ზღვარი, ანუ ორმაგი ინტეგრალი უდრის S ფართობის D: ან, რა არის იგივე, (3) 2.4. ინტეგრალის შეფასება მოდით ფუნქცია /(P) იყოს უწყვეტი შეზღუდულ დახურულ რეგიონში D, მოდით M და mn იყოს /(P)-ის უდიდესი და უმცირესი მნიშვნელობები D რეგიონში და 5 მისი ფართობი. შემდეგ (4) 2.5. დამატება: თუ ფუნქცია /(P) ინტეგრირებადია D დომენში და დომენი Z) იყოფა ორ დომენად D\ და Di საერთო შიდა წერტილების გარეშე, მაშინ /(P) ინტეგრირებადია თითოეულ დომენზე D\ და Di. და (5) 2.6. საშუალო ღირებულების თეორემა 3 (საშუალო მნიშვნელობა). თუ ფუნქცია /(P) უწყვეტია დახურულ შემოსაზღვრულ D დომენში, მაშინ არის D დომენის მინიმუმ ერთი წერტილი Pc ისეთი, რომ ფორმულა და სადაც S არის D დომენის ფართობი მოქმედებს. მართლაც, ვინაიდან /(P) არის უწყვეტი დახურულ შემოსაზღვრულ D დომენში, შემდეგ ის იღებს D-ში მის უდიდეს მნიშვნელობას M და მის უმცირეს მნიშვნელობას m. თვისებით 4 ინტეგრალის შეფასებაზე გვაქვს, ამრიგად, რიცხვი მოთავსებულია უდიდესსა და უმცირესს შორის. ფუნქციის /(P) მნიშვნელობები D დომენში. ფუნქციის /( P) უწყვეტობის გამო D დომენში, რაღაც მომენტში Pc G D იღებს ამ რიცხვის ტოლ მნიშვნელობას, საიდანაც S მნიშვნელობა f( Pc), განსაზღვრული ფორმულით (7), ეწოდება f(P) ფუნქციის საშუალო მნიშვნელობა D დომენში. საშუალო მნიშვნელობის თეორემის მნიშვნელობის გეომეტრიული მნიშვნელობა თუ D რეგიონში ფუნქცია /(P) ^ O, მაშინ ფორმულა (6) ნიშნავს, რომ არის სწორი ცილინდრი D ფუძით (მისი ფართობი არის 5) და სიმაღლე H = /(Pc), რომლის მოცულობა ტოლია ცილინდრული სხეულის მოცულობის (ნახ. 3). § 3. ორმაგი ინტეგრალის დაყვანა გამეორებულ ინტეგრალზე ორმაგი ინტეგრალის გამოთვლის ერთ-ერთი ეფექტური გზაა მისი დაყვანა გამეორებულ ინტეგრალამდე. 3.1. მართკუთხედის შემთხვევა მოდით D ფართობი იყოს დახურული მართკუთხედი P, რომლის გვერდები კოორდინატთა ღერძების პარალელურია. F(x, y) ფუნქცია უწყვეტი იყოს P მართკუთხედში. ორმაგი ინტეგრალი შეიძლება განიმარტოს, როგორც ცილინდრული სხეულის (ალგებრული) მოცულობა P ფუძით, რომელიც შემოსაზღვრულია ზედაპირით. განვიხილოთ შესაბამისი ცილინდრული სხეული. დავხატოთ სიბრტყე Oy ღერძზე პერპენდიკულარული (სურ. 4). ეს სიბრტყე ამოკვეთს ცილინდრულ სხეულს მრუდი ტრაპეციის გასწვრივ, რომელიც შემოიფარგლება ზემოდან ბრტყელი ხაზით z, აღწერილი განტოლებებით. ტრაპეციის ფართობი ABC\A\ გამოიხატება ინტეგრალით, სადაც ინტეგრაცია ხორციელდება x-ზე და yo. - ინტეგრანტის მეორე არგუმენტი - განიხილება როგორც მუდმივი (c ^ Uo ^ d ). ინტეგრალის (1) მნიშვნელობა დამოკიდებულია მნიშვნელობის არჩევანზე. დავსვათ (2) გამოხატულება (2) იძლევა ცილინდრული სხეულის განივი კვეთის ფართობს a y-ის ფუნქციით. მაშასადამე, ცილინდრული სხეულის მოცულობა შეიძლება გამოითვალოს ფორმულის გამოყენებით. მეორეს მხრივ, ეს მოცულობა გამოიხატება ფუნქციის ორმაგი ინტეგრალით /(x, y) ოთხკუთხედზე P. ეს ნიშნავს, რომ S(y) ჩანაცვლება მისი გამოხატულება (2), ვიღებთ ორმაგი ინტეგრალის კონცეფციამდე მიმავალ პრობლემას. ფართობის ელემენტი მრუდი კოორდინატებში იაკობიანი და მისი გეომეტრიული მნიშვნელობა ცვლადების ჩანაცვლების ფორმულა ორმაგ ინტეგრალში ორმაგი ინტეგრალი პოლარულ კოორდინატებში. ბოლო კავშირი ჩვეულებრივ იწერება შემდეგნაირად. სიბრტყეები x = x0. ეს მივყავართ ფორმულამდე (4) თითოეული გამონათქვამი ფორმულების მარჯვენა მხარეს (3) და (4) შეიცავს /(x, y) ფუნქციის ჩვეულებრივი ინტეგრაციის ორ თანმიმდევრულ ოპერაციას. მათ უწოდებენ /(x, y) ფუნქციის განმეორებით ინტეგრალებს P დომენზე. თუ f(x, y) უწყვეტია დახურულ P ოთხკუთხედში, მაშინ განმეორებით ინტეგრალებზე გადასვლა ყოველთვის შესაძლებელია და (5) ე.ი. უწყვეტი ფუნქციის /(x, y) განმეორებითი ინტეგრალების მნიშვნელობები არ არის დამოკიდებული ინტეგრაციის თანმიმდევრობაზე. მაგალითი 1. იპოვეთ ფუნქციის ორმაგი ინტეგრალი დომენზე, რომელიც გვაქვს (იხ. სურ. 5): 3.2. თვითნებური დომენის შემთხვევა მოდით, ახლა დავუშვათ, რომ ინტეგრაციის დომენი არის თვითნებური შეზღუდული კვადრატული დახურული დომენი D xOy სიბრტყეზე, რომელიც აკმაყოფილებს შემდეგ პირობას: Oy ღერძის პარალელურად ნებისმიერი სწორი ხაზი კვეთს D დომენის საზღვარს no. ორ წერტილზე მეტი ან მთელი სეგმენტის გასწვრივ (ნახ. 6 ა). მოდით ჩავსვათ D ფართობი მართკუთხედის შიგნით, როგორც ნაჩვენებია ნახ. 66. სეგმენტი [a, 6] არის D რეგიონის ორთოგონალური პროექცია Oxy ღერძზე, ხოლო სეგმენტი [c, dj არის D რეგიონის ორთოგონალური პროექცია Oy ღერძზე. A და C წერტილები ყოფს D ფართობის საზღვარს ორ მრუდად ABC და AEC. თითოეული ეს მრუდი კვეთს თვითნებურ სწორ ხაზს Oy ღერძის პარალელურად არა უმეტეს ერთ წერტილში. მაშასადამე, მათი განტოლებები შეიძლება დაიწეროს y-ის მიმართ გადაწყვეტილი ფორმით: მოდით, f(x, y) იყოს რაიმე უწყვეტი ფუნქცია D რეგიონში. მოდით, განსახილველი ცილინდრული სხეული სიბრტყით გავანაწილოთ. განყოფილებაში ვიღებთ მრუდი ტრაპეციას PQMN (ნახ. 7), რომლის ფართობი გამოიხატება /(x, y) ფუნქციის ჩვეულებრივი ინტეგრალით, რომელიც განიხილება ერთი ცვლადის ფუნქციად. ამ შემთხვევაში, y ცვლადი იცვლება P წერტილის ორდინატიდან Q წერტილის ორდინატამდე \ წერტილი P არის x = const (სიბრტყეში) წრფის „შესვლა“ რეგიონში - მისი „გასასვლელი“ წერტილი. ამ რეგიონიდან. ვინაიდან ABC მრუდის განტოლება არის და მრუდი არის, აღებული x-ის ეს ორდინატები შესაბამისად ტოლია. შესაბამისად, ინტეგრალი გვაძლევს გამოხატულებას ცილინდრული სხეულის ბრტყელი მონაკვეთის ფართობისთვის, როგორც ჭრის სიბრტყის პოზიციის ფუნქცია x = const. მთელი სხეულის მოცულობა ტოლი იქნება ამ გამოხატვის ინტეგრალის x-ზე ცვლილების ინტერვალში. ამრიგად, კერძოდ, D რეგიონის S ფართობისთვის მივიღებთ: ახლა დავუშვათ, რომ ყოველი სწორი ხაზი კვეთს D რეგიონის საზღვარს არაუმეტეს ორ წერტილზე P და Q, რომელთა აბსციები, შესაბამისად, ტოლია ( ან მთელი სეგმენტის გასწვრივ) (სურ. 8). მსგავსი მსჯელობის განხორციელებისას მივდივართ ფორმულამდე, რომელიც ასევე ამცირებს ორმაგი ინტეგრალის გამოთვლას განმეორებით. მაგალითი 2. გამოთვალეთ ფუნქციის ორმაგი ინტეგრალი D ფართობზე, რომელიც შემოსაზღვრულია ხაზებით ^ პირველი მეთოდი. გამოვსახოთ ინტეგრაციის ველი D. სწორი წრფე y = x და პარაბოლა y = x2 იკვეთება წერტილებზე). ეს ნიშნავს, რომ x იცვლება 8 ლიმიტის ფარგლებში 0-დან. ნებისმიერი სწორი ხაზი x = const) კვეთს რეგიონის საზღვარს არაუმეტეს ორ წერტილზე. აქედან გამომდინარე, ფორმულა (8) გამოიყენება: მეორე მეთოდი (ნახ. 10). ფორმულის გამოყენებით (10). ვიღებთ იგივე შედეგს: მაგალითი 3. გამოვთვალოთ სხეულის მოცულობა, რომელიც შემოსაზღვრულია xOy სიბრტყით გადაკვეთილი ზედაპირით, ნახევარღერძებით ელიფსის ხაზის გასწვრივ ამ სხეულის სიმეტრიის გამო xOz და y Ox კოორდინატულ სიბრტყეებთან მიმართებაში. ვიღებთ: შენიშვნა. თუ რეგიონი D ისეთია, რომ ზოგიერთი სწორი ხაზი (ოსტრათეკული ან ჰორიზონტალური) კვეთს მის საზღვარს ორზე მეტ წერტილზე, მაშინ D რეგიონზე ორმაგი ინტეგრალის გამოსათვლელად, სათანადოდ უნდა გაიყოს იგი ნაწილებად, გაიმეოროს თითოეული ინტეგრალი ნაწილებად. , და დაამატეთ მიღებული შედეგები . მაგალითი 4. გამოთვალეთ ორმაგი ინტეგრალი D ფართობზე, რომელიც ჩაკეტილია ორ კვადრატს შორის ცენტრებით და საწყისსა და გვერდებზე კოორდინატთა ღერძების პარალელურად, თუ შიდა კვადრატის გვერდი არის 2, ხოლო გარე 4. ის უწყვეტია როგორც დიდი კვადრატი Q, რომლის გვერდი არის 4 და პატარა კვადრატში R. რომლის გვერდი უდრის 2-ს (სურ. 12). 1-ლი თეორემის მიხედვით, e*** ფუნქციის ინტეგრალები არსებობს მითითებულ კვადრატებზე, ამიტომ საჭირო ინტეგრალის მნიშვნელობა §4. ცვლადების ცვლილება ორმაგ ინტეგრალში 4.1. წერტილის მრუდი კოორდინატების კონცეფცია მოდით, uOv სიბრტყის D* რეგიონში მოცემული იყოს წყვილი ფუნქცია, რომელიც განვიხილავთ უწყვეტად ამ რეგიონში და აქვს უწყვეტი ნაწილობრივი წარმოებულები. (1) განტოლების ძალით, D* დომენის M*(α, v) ყოველი წერტილი შეესაბამება xOy სიბრტყეში M(x, y) ერთ კონკრეტულ წერტილს და, შესაბამისად, D* დომენის წერტილები შეესაბამება ა. D წერტილების გარკვეული ნაკრები (x, y) xOy სიბრტყეში (ნახ. 13). ამ შემთხვევაში, ისინი ამბობენ, რომ ფუნქციები (1) ასახავს D4 დომენს D სიმრავლეზე. დავუშვათ, რომ სხვადასხვა წერტილი (u, v) შეესაბამება სხვადასხვა წერტილს (x, y). ეს უდრის (1) განტოლებების უნიკალურ ამოხსნადობას u, v-სთან მიმართებაში: ამ შემთხვევაში, რუკს ეწოდება D* დომენის ერთი-ერთზე დახატვა D დომენზე. ასეთი ტრანსფორმაციის დროს, ნებისმიერი. უწყვეტი მრუდი L*, რომელიც მდებარეობს D* დომენში, გადავა უწყვეტ მრუდში L, რომელიც მდებარეობს D რეგიონში. თუ ფუნქციები d(x) y) და h(x, y) ასევე უწყვეტია, მაშინ ნებისმიერი უწყვეტი ხაზის LCD დახმარებით. ტრანსფორმაციის (2) გადავა უწყვეტი ხაზი L* C D*. მოცემული წყვილის Ш, Vo ცვლადების მნიშვნელობებისთვის და, v რეგიონიდან D*, შესაძლებელია ცალსახად განისაზღვროს არა მხოლოდ M*(u) წერტილის პოზიცია.<)> Vq) რეგიონში £)* თავად, მაგრამ შესაბამისი წერტილის M(xo, vo) პოზიცია D რეგიონში, xo = 4>(io, v0), 3/0 = o, vo). ეს იძლევა საფუძველს, განვიხილოთ რიცხვები u, v, როგორც xOy სიბრტყეზე M რეგიონის D წერტილის ახალი კოორდინატები. მათ უწოდებენ M წერტილის მრუდი კოორდინატებს. D ზონის წერტილების სიმრავლეს, რომლისთვისაც ერთ-ერთი კოორდინატი მუდმივი რჩება, კოორდინატთა წრფე ეწოდება. (1) ფორმულაში u = vq ვაყენებთ, ვიღებთ კოორდინატთა წრფის პარამეტრულ განტოლებებს, აქ პარამეტრის როლს ასრულებს ცვლადი u. კოორდინატისთვის v სხვადასხვა (ამისთვის შესაძლებელია) მუდმივი მნიშვნელობების მიცემით, ვიღებთ კოორდინატთა ხაზების ოჯახს (v = const) xOy სიბრტყეზე. ანალოგიურად, ჩვენ ვიღებთ კოორდინატთა ხაზების სხვა ოჯახს (u = const). თუ D* და D რეგიონებს შორის არის ერთი-ერთზე შესაბამისობა, ერთი და იმავე ოჯახის სხვადასხვა კოორდინატთა ხაზები არ იკვეთება ერთმანეთს და თითოეული ოჯახიდან ერთი ხაზი გადის D რეგიონის ნებისმიერ წერტილში. მრუდი კოორდინატთა ხაზების ბადე xOp სიბრტყეზე არის მართკუთხა ბადის გამოსახულება uOv სიბრტყეზე (იხ. სურ. 13). 4.2. ფართობის ელემენტი მრუდი კოორდინატებში. იაკობიანი და მისი გეომეტრიული მნიშვნელობა მოდით ავირჩიოთ D* რეგიონში Uo*V სიბრტყეზე პატარა მართკუთხედი P*P?P$Pl გვერდებით პარალელურად კოორდინატთა ღერძებით 0*u და O"v და გვერდების სიგრძე Ai და Av. (განსაზღვრულობისთვის ვივარაუდოთ, რომ A ) შესაბამისად (ნახ. 14 ა) მისი ფართობი მართკუთხედი გარდაიქმნება მრუდი ოთხკუთხედად * D არეში (ნახ. 146). თუ P წვეროებს აქვთ კოორდინატები, მაშინ ფორმულების მიხედვით (1). ), Pi-ს შესაბამის წვეროებს აქვთ კოორდინატები), ტეილორის ფორმულის გამოყენებით ორი ცვლადის ფუნქციისთვის და შემოვიფარგლებით A-სა და Av-თან შედარებით პირველი რიგის/პკ ტერმინებით, მივიღებთ შემდეგ სავარაუდო კოორდინატთა მნიშვნელობებს a-ს წვეროებისთვის. ოთხკუთხედი, სადაც ფუნქციები და მათი წარმოებულები გამოითვლება წერტილში). წერტილების კოორდინატებისთვის ნაპოვნი გამონათქვამები აჩვენებს, რომ მცირე უმაღლესი რიგის ოთხკუთხედი P\PiPiPa არის პარალელოგრამი. ოთხკუთხედი შეიძლება იყოს დაახლოებით გამოსახული ვექტორული ნამრავლის სიგრძით, პრობლემა, რომელიც იწვევს ორმაგი ინტეგრალის კონცეფციას. განმეორებითი ერთი ცვლადების ჩანაცვლება ორმაგ ინტეგრალში ფართობის ელემენტი მრუდხაზოვან კოორდინატებში იაკობიანი და მისი გეომეტრიული მნიშვნელობა ცვლადების შეცვლის ფორმულა ორმაგ ინტეგრალში ორმაგი ინტეგრალი პოლარულ კოორდინატებში განმსაზღვრელი ვიდეოს (7) და (8) ფორმულებიდან, იაკობის აბსოლუტური მნიშვნელობა ასრულებს D რეგიონის ლოკალური გაჭიმვის კოეფიციენტის როლს" (ამ პუნქტში (tx, v)) როდესაც მას ასახავს D დომენზე ტრანსფორმაციის ფორმულების გამოყენებით (1). 4.3. ორმაგ ინტეგრალში ცვლადების შეცვლის ფორმულა მოდით, უწყვეტმა ფუნქციებმა განახორციელონ D* დომენის ერთი-ერთზე დახატვა D-ზე და ჰქონდეს პირველი რიგის უწყვეტი ნაწილობრივი წარმოებულები. მოდით, xOy სიბრტყეზე D რეგიონში მოცემული იყოს უწყვეტი ფუნქცია. ფუნქციის თითოეული მნიშვნელობა) D რეგიონში შეესაბამება r = ფუნქციის ტოლ მნიშვნელობას D რეგიონში", სადაც. გავყოთ რეგიონი D*. ნაწილობრივ რეგიონებად და შექმენით D რეგიონის შესაბამისი დანაყოფი. შეარჩიეთ წერტილები შესაბამის ნაწილობრივ რეგიონებში (u, v) და (x, y) ისე, რომ მათში არსებული ფუნქციების მნიშვნელობები ემთხვეოდეს და შევადგინოთ ინტეგრალური ჯამები. z = /(x, y) და v) ფუნქციები D და D* დომენებზე. ვიღებთ ფუნქციების იაკობიანს. მივდივართ ტოლობაზე (9) ზღვრამდე, როგორც D\ ნაწილობრივი რეგიონების უდიდესი დიამეტრი d* მიდრეკილია. ნულამდე (რუკის უწყვეტობის გამო (I), D-ში ნაწილობრივი რეგიონების d დიამეტრიდან ყველაზე დიდი იქნება ნულისკენ), გვექნება, სადაც პირობა J Ф 0 არის პირობა ლოკალური ერთი-ერთზე შესრულებული რუქაზე. ფუნქციების თეორემა 4. იმისათვის, რომ დეკარტის კოორდინატებში მითითებული ორმაგი ინტეგრალი მრუდისხაზოვან კოორდინატებში ორმაგ ინტეგრალად გარდაიქმნას, საჭიროა ცვლადების x და y ჩანაცვლება ინტეგრანდულ ფუნქციაში /(x, y) შესაბამისად ფართობის გავლით. ელემენტი dx dy - მისი გამოხატვა მრუდის კოორდინატებში: მაგალითი. იპოვნეთ ჰიპერბოლებით შემოსაზღვრული ფიგურის ფართობი m. მითითებული ფიგურის ფართობის პოვნა ხდება ორმაგი ინტეგრალის გამოთვლაზე O რეგიონზე. მოდით შემოვიტანოთ ახალი, მრუდი კოორდინატები და o ფორმულებით მდგომარეობიდან განტოლების, რომ. ეს ნიშნავს, რომ uOv სიბრტყეში მივიღეთ მართკუთხედი (სურ. 156) - ფიგურა უფრო მარტივი ვიდრე მოცემული ფიგურა D. გამოვხატოთ x და y მიმართებებიდან (11) u და t>: სურ. 15 შემდეგ ორმაგი ინტეგრალი. პოლარულ კოორდინატებში ორმაგი ინტეგრალის გამოთვლა ხშირად გამარტივებულია მართკუთხა კოორდინატების x და y პოლარული კოორდინატებით ფორმულების მიხედვით ჩანაცვლებით. პოლარული კოორდინატები შეიძლება ჩაიწეროს შემდეგნაირად: ამ შემთხვევაში (13) ფართობის ელემენტი პოლარულ კოორდინატებში შეიძლება მივიღოთ გეომეტრიული მოსაზრებებიდან (იხ. სურ. 16). დაჩრდილული უბნის ფართობი ფიგურაში A = pl. სექტორები. სექტორები უმაღლესი რიგის უსასრულო რაოდენობის უგულებელყოფით, ვიღებთ და ვიღებთ მას, როგორც ფართობის ელემენტს პოლარულ კოორდინატებში. ასე რომ, იმისთვის, რომ დეკარტის კოორდინატებში ორმაგი ინტეგრალი გადააქციოთ ორმაგ ინტეგრალში პოლარულ კოორდინატებში, თქვენ უნდა შეცვალოთ a: და y ინტეგრანდში p costp-ით და psini-ით, შესაბამისად, და შეცვალოთ ფართობის ელემენტი დეკარტის კოორდინატებში dx dy-ით. ფართობის ელემენტი პოლარულ კოორდინატებში p dp dip. ახლა დავიწყოთ ორმაგი ინტეგრალის გამოთვლა პოლარულ კოორდინატებში. როგორც მართკუთხა დეკარტის კოორდინატების შემთხვევაში, ინტეგრალის გამოთვლა პოლარულ კოორდინატებში ხორციელდება მისი განმეორებით ინტეგრალამდე შემცირებით. ჯერ განვიხილოთ შემთხვევა, როდესაც O პოლუსი მდებარეობს D რეგიონის გარეთ. დაე, D რეგიონს ჰქონდეს თვისება, რომ პოლუსიდან გამომავალი ნებისმიერი სხივი (კოორდინატთა ხაზი კვეთს მის საზღვარს არაუმეტეს ორ წერტილზე ან მთელ სეგმენტზე. (ნახ. 17) გაითვალისწინეთ პოლარული კუთხის უკიდურესი მნიშვნელობები i არის გარე ინტეგრაციის საზღვრები. სხივი μ> = გადის D რეგიონის კონტურის A წერტილში, ხოლო სხივი B წერტილში. წერტილები Aw B. დაყავით D რეგიონის კონტური ორ ნაწილად: ACB და AFB. მოდით იყოს მათი პოლარული განტოლებები და) არის ერთმნიშვნელოვანი უწყვეტი ფუნქციები, რომლებიც აკმაყოფილებენ პირობას. ფუნქციები არის შიდა ინტეგრაციის საზღვრები. განმეორებით ინტეგრალებზე გადასვლისას ვიღებთ შემდეგ ფორმულას, კერძოდ, D რეგიონის S ფართობისთვის F(p, r 1) ვიღებთ ახლა პოლუსი O მდებარეობს D რეგიონის შიგნით. დავუშვათ, რომ რეგიონი D. არის ვარსკვლავური პოლუსთან მიმართებაში, ანუ ნებისმიერი სხივი tp = const კვეთს რეგიონის საზღვარს მხოლოდ ერთ წერტილში ან მთელ სეგმენტზე (ნახ. 18). მოდით იყოს რეგიონის საზღვრის განტოლება პოლარულ კოორდინატებში. ნახ.18 მაგალითი.გამოთვალეთ ინტეგრალი, სადაც რეგიონი არის პირველ კვადრატში მდებარე ერთეული წრის მეოთხედი.გადავიდეთ პოლარულ კოორდინატებზე მაშინ ინტეგრაციის დომენი იქნება მართკუთხედი გარდაქმნილი ინტეგრალი / ადვილად გამოითვლება: d შენიშვნა: თუ იაკობიანი არ არის ნული D დომენში, მაშინ ამ დომენის თითოეული წერტილის გარკვეულ სამეზობლოში რუკება არის ერთი-ერთზე. თუმცა, შეიძლება მოხდეს, რომ მთელი დომენის რუქა არ იყოს ერთი-ერთზე. განვიხილოთ ფუნქციებით განსაზღვრული ასახვა, ამ ფუნქციების იაკობიანი ტოლია და, შესაბამისად, ყველგან განსხვავდება ნულისაგან. მიუხედავად ამისა, ჩვენ ვიღებთ ამისთვის, ასე რომ, ეს რუქა არ არის ერთი-ერთზე. მეორეს მხრივ, თუ რუკების იაკობიანი გაქრება რაღაც მომენტში, მაშინ, მიუხედავად ამისა, ამ წერტილის სამეზობლოში რუკა შეიძლება აღმოჩნდეს ერთი-ერთზე. მაგალითად, ფუნქციებით განსაზღვრული რუკებისთვის, იაკობიანი უდრის ნულს და ზე, მაგრამ დახატვა არის ერთი-ერთზე. შებრუნებული რუკა განისაზღვრება ფუნქციებით

1.1 ორმაგი ინტეგრალის განმარტება

1.2 ორმაგი ინტეგრალის თვისებები

1°. ადიტიურობა. თუ ფუნქცია f(x, y) ინტეგრირებადია D რეგიონში და თუ რეგიონი D იყოფა მრუდით Г ნულოვანი ფართობის ორ დაკავშირებულ რეგიონად D1 და D2, რომლებსაც არ აქვთ საერთო შიდა წერტილები, მაშინ ფუნქცია f(x , y) ინტეგრირებადია თითოეულში D 1 და D 2 უბნებიდან და

2°. ხაზოვანი თვისება. თუ f(x, y) და g(x, y) ფუნქციები ინტეგრირებადია D დომენში, ჰა? და? - ნებისმიერი რეალური რიცხვი, შემდეგ ფუნქცია [? · f(x, y) + ?· g(x, y)] ასევე ინტეგრირებადია D დომენში და

3°. თუ f(x, y) და g(x, y) ფუნქციები ინტეგრირებადია D დომენში, მაშინ ამ ფუნქციების ნამრავლი ასევე ინტეგრირებადია D-ში.

4°. თუ ფუნქციები f(x, y) და g(x, y) ინტეგრირებადია D დომენში და ყველგან ამ დომენში f(x, y) ? g (x, y), შემდეგ

5°. თუ ფუნქცია f(x, y) ინტეგრირებადია D დომენში, მაშინ ფუნქცია |f(x, y)| ინტეგრირებადი დომენში D და

(რა თქმა უნდა, |f(x, y)|-ის ინტეგრირება D-ში არ ნიშნავს f(x, y)-ის ინტეგრირებას D-ში.)

6°. საშუალო მნიშვნელობის თეორემა. თუ ორივე ფუნქცია f(x, y) და g(x, y) ინტეგრირებადია D დომენში, ფუნქცია g(x, y) არის არაუარყოფითი (არადადებითი) ყველგან ამ დომენში, M და m არის f( x, y) ფუნქციის უმაღლესი და infimum D დომენში, მაშინ არის რიცხვი?, რომელიც აკმაყოფილებს m უტოლობას? ? ? M და ისეთი, რომ ფორმულა მოქმედებს

კერძოდ, თუ ფუნქცია f(x, y) უწყვეტია D-ში და D დომენი დაკავშირებულია, მაშინ ამ დომენში არის წერტილი (?, ?) ისეთი, რომ? = f(?, ?), და ფორმულა იღებს ფორმას

7°. მნიშვნელოვანი გეომეტრიული თვისება. უდრის D რეგიონის ფართობს

სივრცეში მოცემული იყოს T სხეული (ნახ. 2.1), რომელიც ქვემოდან შემოიფარგლება D რეგიონით, ზემოდან - უწყვეტი და არაუარყოფითი ფუნქციის გრაფიკით) z=f (x, y), რომელიც განისაზღვრება რეგიონი D, გვერდებიდან - ცილინდრული ზედაპირით, რომლის მეგზურია სასაზღვრო რეგიონი D, ხოლო გენერატორები ოზის ღერძის პარალელურია. ამ ტიპის სხეულს ცილინდრული სხეული ეწოდება.

1.3 ორმაგი ინტეგრალის გეომეტრიული ინტერპრეტაცია

1.4 მართკუთხედის ორმაგი ინტეგრალის კონცეფცია

მოდით განისაზღვროს თვითნებური ფუნქცია f(x, y) ყველგან ოთხკუთხედზე R = ? (იხ. სურ. 1).

დავყოთ სეგმენტი a? x? b n ნაწილობრივ სეგმენტად a = x 0 წერტილების გამოყენებით< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.

ეს დანაყოფი Ox და Oy ღერძების პარალელურად სწორი ხაზების გამოყენებით შეესაბამება R მართკუთხედის დაყოფას n · p ნაწილობრივ ოთხკუთხედებად R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). მართკუთხედის R მითითებულ დანაყოფს აღვნიშნავთ T სიმბოლოთი. შემდგომ ამ ნაწილში ტერმინი „მართკუთხედი“ გაგებული იქნება, როგორც მართკუთხედი, რომლის გვერდები კოორდინატთა ღერძების პარალელურია.

თითოეულ ნაწილობრივ მართკუთხედზე R kl ჩვენ ვირჩევთ თვითნებურ წერტილს (? k, ? l). ?x k = x k - x k-1, ?y l = y l - y l-1, ჩვენ აღვნიშნავთ?R kl მართკუთხედის R kl ფართობს. ცხადია, ?R kl = ?x k ?y l .

ეწოდება f(x, y) ფუნქციის ინტეგრალური ჯამი, რომელიც შეესაბამება R მართკუთხედის T მოცემულ ნაწილს და T დანაყოფის ნაწილობრივ მართკუთხედებზე შუალედური წერტილების (? k, ? l) მოცემულ არჩევანს.

დიაგონალს დავარქმევთ მართკუთხედის დიამეტრს R kl. Სიმბოლო? ყველა ნაწილობრივი მართკუთხედის დიამეტრებიდან ყველაზე დიდი ავღნიშნოთ R kl-ით.

I რიცხვს ეწოდება ინტეგრალური ჯამების ზღვარი (1) ზე? > 0 თუ რაიმე დადებითი რიცხვისთვის? შეგიძლიათ მიუთითოთ ასეთი დადებითი რიცხვი?, თუ?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство

| ? - მე |< ?.

ფუნქციას f(x, y) ეწოდება რიმანის ინტეგრირებადი ოთხკუთხედზე R, თუ არსებობს ამ ფუნქციის ინტეგრალური ჯამების სასრული ზღვარი I? > 0.

მითითებულ ზღვარს I ეწოდება f(x, y) ფუნქციის ორმაგი ინტეგრალი R მართკუთხედზე და აღინიშნება ერთ-ერთი შემდეგი სიმბოლოთი:

კომენტარი. ისევე, როგორც ერთი განსაზღვრული ინტეგრალისთვის, დადგენილია, რომ R მართკუთხედზე ინტეგრირებული ნებისმიერი ფუნქცია f(x, y) შემოიფარგლება ამ მართკუთხედზე.

ეს იძლევა იმის საფუძველს, რომ განვიხილოთ მხოლოდ შეზღუდულ ფუნქციებში f(x, y).

ორმაგი ინტეგრალის ცნებამდე მიმავალი პრობლემა.

დავუშვათ, რომ ნაწილების ფუნქცია განსაზღვრულია და ჩაწერეთ თანხა

რომელსაც ინტეგრალი ეწოდება.

პასუხი: ფუნქციისა და არჩევნის განსაზღვრული ინტეგრალის (დ.ი.) ქვეშ

Დანიშნულება:

ციფრებს უწოდებენ რიმანის ინტეგრირებადი.

თ არსებობა: იმ პირობით, რომ .

ო.ი.-ის განმარტების შესაბამისად. ჩვენ აღვნიშნავთ, რომ ინტეგრალი დამოკიდებულია ტიპზე, საზღვრებზე და, მაგრამ არ არის დამოკიდებული ცვლადის აღნიშვნის სიმბოლოზე, სხვაგვარად გამოხატული

17.1.1 და 17.1.2 პუნქტებისა და ო.ი.-ის განმარტების შესაბამისად. მოდით ჩამოვწეროთ მრუდი ტრაპეციის ფართობის ფორმულა: , ძალის მუშაობა

ზე:

ორმაგი ინტეგრალის, ინტეგრალური ჯამების ცნება.

ორმაგი ინტეგრალის არსებობა, ანუ ინტეგრალური ჯამის ზღვარი, აშკარად ჩანს, რადგან ეს ზღვარი იძლევა ცილინდრული სხეულის მოცულობას. თუმცა, ეს მსჯელობა არ არის მკაცრი. უფრო სრულყოფილ კურსებში ეს დებულება მკაცრად არის დადასტურებული და ეწოდება ორმაგი ინტეგრალის არსებობის თეორემა.

არსებობის თეორემა. ნებისმიერი ფუნქციისთვის, რომელიც უწყვეტია შეზღუდულ დახურულ რეგიონში, რომელსაც აქვს ფართობი a, არის ორმაგი ინტეგრალი, ანუ არის ინტეგრალური ჯამების ზღვარი მცირე ფართობების რაოდენობის შეუზღუდავი ზრდით, იმ პირობით, რომ თითოეული მათგანი იკუმშება წერტილი. ეს ზღვარი არ არის დამოკიდებული რეგიონის ნაწილებად დაყოფის მეთოდზე ან პუნქტების არჩევანზე

შემდგომში განვიხილავთ მხოლოდ ფუნქციებს, რომლებიც უწყვეტია ინტეგრაციის სფეროში.

არსებობის თეორემიდან გამომდინარეობს, რომ შეგვიძლია, მაგალითად, a რეგიონი დავყოთ პატარა მართკუთხედებად, სწორი გვერდებით კოორდინატთა ღერძების პარალელურად (სურ. 230). სადაც. შემდეგ თითოეულ პატარა ოთხკუთხედში წერტილის არჩევით შეგვიძლია დავწეროთ ორმაგი ინტეგრალის განმარტების მიხედვით

იმისათვის, რომ ხაზგასმით აღვნიშნოთ, რომ ორმაგი ინტეგრალი შეიძლება მივიღოთ, როგორც ფორმის ჯამის ზღვარი, აღნიშვნის ნაცვლად, ჩვენ ასევე ვიყენებთ აღნიშვნას.

გამონათქვამს ეწოდება ფართობის ელემენტი დეკარტის კოორდინატებში და უდრის მართკუთხედის ფართობს, რომლის გვერდები კოორდინატთა ღერძების პარალელურია.

გაითვალისწინეთ, რომ ინტეგრალური ჯამის შედგენისას, a ფართობის საზღვრის მიმდებარე უბნებს არ აქვთ მართკუთხედის ფორმა. თუმცა, შეიძლება დადასტურდეს, რომ ასეთი უბნების ლიმიტში მდებარე ფართობებით მართკუთხედებით ჩანაცვლების შეცდომა ნულამდე შემცირდება.

ორმაგი ინტეგრალის თვისებები

(რა თქმა უნდა, ინტეგრაციიდან | ვ(x, წ)| ვ დინტეგრირება არ მოჰყვება ვ(x, წ) ვ დ.)

კერძოდ, თუ ფუნქცია ვ(x, წ) არის უწყვეტი დდა ტერიტორია დ თანმიმდევრული, მაშინ ამ რეგიონში არის ასეთი წერტილი ( ξ , η ), Რა μ = ვ(ξ , η ) და ფორმულა (11) იღებს ფორმას

ორი ცვლადის ფუნქციისთვის, რომელიც მითითებულია როგორც ზ = ვ(x, წ) .

ორმაგი ინტეგრალი იწერება შემდეგნაირად:

Აქ დ– ხაზებით შემოსაზღვრული ბრტყელი ფიგურა, რომლის გამოსახულებები (ტოლობები) მოცემულია ორმაგი ინტეგრალის გამოთვლის ამოცანაში. მარცხენა და მარჯვენა არის ტოლობები, რომლებშიც არის ცვლადი მარცხნივ x, და ზემოთ და ქვემოთ – ტოლობებით, რომლებშიც არის ცვლადი მარცხნივ წ. ეს ადგილი კვლავაც არის ერთ-ერთი ყველაზე მნიშვნელოვანი ორმაგი ინტეგრალის გამოთვლის ტექნიკის გასაგებად.

გამოთვალეთ ორმაგი ინტეგრალი - ნიშნავს აღნიშნული ფიგურის ფართობის ტოლი რიცხვის პოვნას დ .

სანამ არ შევეხებით ორმაგი ინტეგრალური განმარტებები და ჩვენ ვისწავლით მის გამოთვლას. უფრო ადვილია იმის გაგება, თუ რა არის ორმაგი ინტეგრალი, როცა მის გამოსათვლელად რამდენიმე ამოცანის ამოხსნა გაქვს, ამიტომ ამ გაკვეთილის ბოლოს იპოვით ორმაგი ინტეგრალის განმარტებას. ცოტა წინ რომ გავიხედოთ, შეგვიძლია მხოლოდ აღვნიშნოთ, რომ ორმაგი ინტეგრალის განმარტება ასევე დაკავშირებულია აღნიშნულ ფიგურასთან. დ .

თუ ფიგურა დარის მართკუთხედი, მისი შემზღუდველი ყველა ხაზი სწორი ხაზებია. თუ ფიგურა დ- არის მრუდი, შემდეგ მარცხნივ და მარჯვნივ შემოიფარგლება სწორი ხაზებით, ხოლო ზემოთ და ქვემოთ მრუდი ხაზებით, მოცემული ტოლობებით, რომლებიც მოცემულია ამოცანაში. არის შემთხვევებიც, როცა ფიგურა დ- სამკუთხედი, მაგრამ უფრო ასეთ შემთხვევებზე ცოტა უფრო შორს.

ორმაგი ინტეგრალის გამოსათვლელად აუცილებელია ფიგურის მოსაზღვრე ხაზების დახარისხება დ, რომელსაც მკაცრი სახელი აქვს - ინტეგრაციის რეგიონი. დაალაგეთ მარცხნივ და მარჯვნივ და ზედა და ქვედა. ეს საჭირო იქნება როცა ორმაგი ინტეგრალის შემცირება გამეორებულ ინტეგრალზე – ორმაგი ინტეგრალის გამოთვლის მეთოდი.

მართკუთხა ფართობის შემთხვევა:

მოხრილი რეგიონის შემთხვევა:

და ეს უკვე ნაცნობი განსაზღვრული ინტეგრალების გამოსავალია, რომელშიც მოცემულია ინტეგრაციის ზედა და ქვედა საზღვრები. გამონათქვამები, რომლებიც განსაზღვრავენ ხაზებს, რომლებიც ზღუდავს ფიგურას დ, იქნება ინტეგრაციის საზღვრები ჩვეულებრივი განსაზღვრული ინტეგრალებისთვის, რომლებსაც უკვე ვუახლოვდებით.

ორმაგი ინტეგრალის შემცირება განმეორებით

მართკუთხა რეგიონის საქმე

მოდით არსებობდეს ორმაგი ინტეგრალი ასეთი ფუნქციისთვის

რომ შეაფასეთ ეს ორმაგი ინტეგრალი , უნდა დავიყვანოთ ის განმეორებით ინტეგრალამდე, რომელსაც აქვს ფორმა

ჯერ უნდა გამოთვალოთ შიდა (მარჯვნივ) განსაზღვრული ინტეგრალი, შემდეგ გარე (მარცხნივ) განსაზღვრული ინტეგრალი.

შეგიძლიათ როლების შეცვლა xდა წ

მაგალითი 1.გამოთვალეთ ორმაგი ინტეგრალი

ჩვენ ვიანგარიშებთ შიდა (მარჯვნივ) ინტეგრალს, განვიხილავთ y-ს მუდმივად. Გავიგეთ.

მაგალითი 2.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზში ჩვენ ვაშენებთ ინტეგრაციის რეგიონს:

ახლა ჩვენ გამოვთვალოთ ახლად გამოთვლილი შიდა (მარჯვნივ) გარე (მარცხნივ) ინტეგრალი:

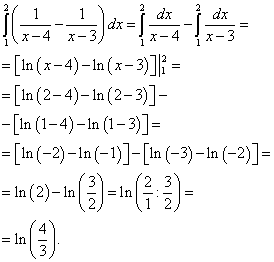
შედეგი იქნება ამ ორმაგი ინტეგრალის გადაწყვეტა.

თავად გამოთვალეთ ორმაგი ინტეგრალი და შემდეგ გადახედეთ ამოხსნას

მოსახვევი ან სამკუთხა რეგიონის შემთხვევა

მოდით კვლავ მოგვცეს ორი ცვლადის ფუნქცია ვ(x, წ) და შეზღუდვები დ: უკვე ოდნავ განსხვავებული ტიპისაა:

ეს ჩანაწერი ნიშნავს, რომ ფიგურა დმარცხენა და მარჯვენა შეზღუდულია, როგორც სწორხაზოვანი რეგიონის შემთხვევაში - სწორი ხაზები x = ადა x = ბ, მაგრამ ქვემოთ და ზემოთ არის მრუდები, რომლებიც მოცემულია განტოლებებით და . სხვა სიტყვებით რომ ვთქვათ, და არის ფუნქციები.

დაე, ასეთ ფუნქციასაც ჰქონდეს ორმაგი ინტეგრალი

ამ ორმაგი ინტეგრალის შესაფასებლად, ჩვენ უნდა დავიყვანოთ ის განმეორებით ინტეგრალზე, რომელსაც აქვს ფორმა

აქ არის ინტეგრაციის საზღვრები ადა ბ- რიცხვები და და - ფუნქციები. სამკუთხა რეგიონის შემთხვევაში, ერთ-ერთი ფუნქცია ან არის სწორი ხაზის განტოლება. ეს შემთხვევა განხილული იქნება მაგალით 3-ში.

როგორც მართკუთხა რეგიონის შემთხვევაში, ჯერ უნდა გამოთვალოთ სწორი განსაზღვრული ინტეგრალი, შემდეგ მარცხენა განსაზღვრული ინტეგრალი.

ანალოგიურად, შეგიძლიათ როლების შეცვლა xდა წ. შემდეგ განმეორებით ინტეგრალს ექნება ფორმა

ასეთი განმეორებითი ინტეგრალი ზუსტად ასე უნდა გადაწყდეს: ჯერ - შიდა (მარჯვნივ) ინტეგრალი, შემდეგ - გარე (მარცხნივ).

მაგალითი 5.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზზე ვაშენებთ ინტეგრაციის რეგიონს და ვხედავთ, რომ ის სამკუთხაა:

ჩვენ ვიანგარიშებთ შიდა (მარჯვნივ) ინტეგრალს, განვიხილავთ x მუდმივად. Გავიგეთ.

ახლა ჩვენ გამოვთვალოთ ახლად გამოთვლილი შიდა (მარჯვნივ) გარე (მარცხნივ) ინტეგრალი. ჯერ ამ ინტეგრალს წარმოვადგენთ ინტეგრალების ჯამის სახით:

ჩვენ ვიანგარიშებთ პირველ ტერმინს:

ჩვენ ვიანგარიშებთ მეორე ტერმინს:

ჩვენ ვიანგარიშებთ მესამე ტერმინს:

ჩვენ ვიღებთ ჯამს, რომელიც იქნება ამ ორმაგი ინტეგრალის ამონახსნი:

მაგალითი 6.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზში ჩვენ ვაშენებთ ინტეგრაციის რეგიონს:

შედეგი იქნება ამ ორმაგი ინტეგრალის გადაწყვეტა.

x-სწორი და არასწორი წ- ინტეგრაციის სწორი და არასწორი დომენები

ეს ხდება, რომ ორმაგი ინტეგრალის ინტეგრაციის დომენი შემოიფარგლება ისეთი ხაზებით, რომ საჭირო ხდება ინტეგრაციის დომენის ნაწილებად დაყოფა და თითოეული შესაბამისი განმეორებითი ინტეგრალის ცალკე გადაჭრა. ეს ის შემთხვევებია, როდესაც:

1) ინტეგრაციის არე არის ფიგურა, რომელსაც აქვს ორი ან მეტი სწორი ან მრუდი ხაზი ქვედა ან ზედა (მარცხნივ ან მარჯვნივ) საზღვრის სახით;

2) ინტეგრაციის რეგიონი არის ფიგურა, რომლის საზღვარი ხაზები იკვეთება ორზე მეტ წერტილზე.

თუ ზემოაღნიშნული ეხება ინტეგრაციის დომენის მარცხენა ან მარჯვენა საზღვარს, ანუ ხაზებით განსაზღვრულ შეზღუდვებს, რომლებიც გამოხატულია x, მაშინ ინტეგრაციის დომენი ეწოდება x- არასწორი. თუ ხაზი წ = წ0 კვეთს შესაბამის საზღვარს მხოლოდ ერთ წერტილში და თუ საზღვარი არის მხოლოდ ერთი სწორი ხაზი ან მრუდი, მაშინ ინტეგრაციის დომენი ე.წ. x- სწორი

ანალოგიურად, თუ ხაზებით განსაზღვრული საზღვარი გამოხატული მეშვეობით წ, სწორი x = x0 იკვეთება ერთზე მეტ წერტილზე ან თუ საზღვარი არის ერთზე მეტი სწორი ხაზი ან მრუდი, მაშინ ინტეგრაციის დომენი ე.წ. წ- არასწორი. ახლა აჩვენეთ ნიშნები წ- სწორი ტერიტორია, სავარაუდოდ, საკმაოდ მარტივია.

აქამდე ჩვენ განვიხილეთ მაგალითები x-არასწორი და წ- ინტეგრაციის სწორი სფეროები. ახლა განვიხილოთ შემთხვევები, როდესაც სისწორის პირობა დარღვეულია.

მაგალითი 7.გამოთვალეთ ორმაგი ინტეგრალი, რომლის ინტეგრაციის დომენი შემოიფარგლება ხაზებით წ = x , xy = 1 , წ = 2 .

გამოსავალი. ინტეგრაციის დომენი არის წ-არასწორია, რადგან მისი ქვედა საზღვარი არ შეიძლება იყოს მითითებული ერთი ხაზით წ = წ(x) . როგორც ზემოთ მოცემულ ფიგურაში ჩანს, ქვედა ზღვარი შედგება წ = x(მუქი შინდისფერი) და xy= 1 (მწვანე). ამიტომ პირდაპირი x= 1 (შავი) ჩვენ შეგვიძლია გავყოთ ინტეგრაციის დომენი ორ ნაწილად - და .

ეს ორმაგი ინტეგრალი გამოითვლება შემდეგნაირად:

ინტეგრაციის რიგის შეცვლა

როგორც ზემოთ აღინიშნა, ორმაგი ინტეგრალის განმეორებით ინტეგრალზე შემცირების შემდეგ, შეგიძლიათ შეცვალოთ ცვლადები xდა წროლები, ან, სხვა სიტყვებით რომ ვთქვათ, შეცვალოს ინტეგრაციის რიგი.

ინტეგრაციის რიგის ცვლილება გადატანითი მნიშვნელობით შეიძლება აისახოს ო’ჰენრის შემდეგი სიტყვებით: „ასე იქცევა ჯუნგლებში მცხოვრები – ცხოველი – გალიაში მოხვედრისას და ასე იქცევა გალიაში ჩასმული ბინადარი – ადამიანი – იქცევა, როცა ეჭვების ჯუნგლებში იკარგება." ო'ჰენრის თქმით, შედეგი იგივეა და იგივე: "ჩალმერსმა წერილი დაარღვია ათას წვრილ ნაჭრად და დაიწყო მისი ძვირადღირებული ხალიჩის ტკეპნა, უკან დახევა და მასზე.” ( ო.ჰენრი. მედისონის სკვერის შეჰერეზადა.)

მაშინ, თუ ჩვენი მარცხენა ინტეგრალი ცვლადზე x, და მარჯვენა - მიერ წ, შემდეგ ინტეგრაციის რიგის შეცვლის შემდეგ ყველაფერი პირიქით იქნება. მაშინ „ახალი“ თამაშისათვის ინტეგრაციის საზღვრები უნდა იყოს „ნასესხები“ „ძველი“ X-დან, ხოლო „ახალი“ X-ის ინტეგრაციის ლიმიტები უნდა იყოს მიღებული ფორმით. შებრუნებული ფუნქცია, x-ისთვის გადაჭრით განტოლება, რომელიც ადგენს y-ს ზღვარს.

მაგალითი 8.

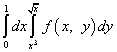გამოსავალი. ინტეგრაციის რიგის შეცვლის შემდეგ, ინტეგრალი y-ზე გახდება მემარცხენე, ხოლო ინტეგრალი x-ზე - მარჯვენა. ჩვენ ვისესხებთ ინტეგრაციის საზღვრებს „ახალი“ თამაშისთვის „ძველი“ X-დან, ანუ ქვედა ზღვარი უდრის ნულს, ხოლო ზედა ზღვარი უდრის ერთს. „ძველი“ თამაშის ინტეგრაციის საზღვრები მოცემულია განტოლებებით და . x-ისთვის ამ განტოლებების ამოხსნის შემდეგ, ვიღებთ ინტეგრაციის ახალ ზღვრებს x-ისთვის:

(ქვედა) და (ზედა).

ამრიგად, ინტეგრაციის რიგის შეცვლის შემდეგ, განმეორებითი ინტეგრალი ჩაიწერება შემდეგნაირად:

ორმაგ ინტეგრალში ინტეგრაციის რიგის შეცვლის შემდეგ, ინტეგრაციის დომენი ხშირად იქცევა წ- არასწორი ან x- არასწორი (იხ. წინა პუნქტი). შემდეგ თქვენ უნდა გაყოთ ინტეგრაციის დომენი ნაწილებად და მოაგვაროთ თითოეული შესაბამისი განმეორებადი ინტეგრალი ცალ-ცალკე.

ვინაიდან ინტეგრაციის სფეროს ნაწილებად დაყოფა ბევრ სტუდენტს უქმნის გარკვეულ სირთულეებს, ჩვენ არ შემოვიფარგლებით წინა აბზაცში მოცემული მაგალითით, მაგრამ განვიხილავთ კიდევ რამდენიმე მაგალითს.

მაგალითი 9.შეცვალეთ ინტეგრაციის რიგი განმეორებადი ინტეგრალისთვის

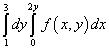გამოსავალი. ამრიგად, ამ განმეორებითი ინტეგრალის ინტეგრაციის არეალი შემოიფარგლება სწორი ხაზებით წ = 1 , წ = 3 , x = 0 , x = 2წ .

სხვადასხვა თანმიმდევრობით ინტეგრირებისას, რეგიონის ქვედა საზღვარი შედგება ორი სწორი ხაზისგან: ABდა ძვ.წ., რომლებიც მოცემულია განტოლებებით წ= 1 და წ = x/2, როგორც ჩანს ქვემოთ მოცემულ ფიგურაში.

ასეთი გაურკვევლობიდან გამოსავალი არის ინტეგრაციის დომენის ორ ნაწილად გაყოფა. ინტეგრაციის დომენის დაყოფა იქნება სწორი ხაზი BM. ჩვენ ვიანგარიშებთ ინტეგრაციის ახალ ზღვრებს ინვერსიული ფუნქციის მოძიებით. ამ ამოხსნის მიხედვით, განმეორებითი ინტეგრალი ინტეგრაციის რიგის შეცვლის შემდეგ იქნება ორი ინტეგრალის ჯამის ტოლი:

ბუნებრივია, იგივე იქნება ორმაგი ინტეგრალის ამოხსნა, რომელიც მცირდება ამ მაგალითის პირობებში მოცემულ განმეორებით ინტეგრალამდე.

მაგალითი 10.შეცვალეთ ინტეგრაციის რიგი განმეორებადი ინტეგრალისთვის

გამოსავალი. ასე რომ, განმეორებითი ინტეგრალის ინტეგრაციის სფერო შემოიფარგლება სწორი ხაზებით x = 0 , x= 2 და მოსახვევები და .

როგორც ქვემოთ მოცემულ ფიგურაში ჩანს, ღერძის პარალელურად სწორი ხაზი 0x, გადაკვეთს ინტეგრაციის დომენის ქვედა საზღვარს ორზე მეტ წერტილზე.

ამრიგად, ინტეგრაციის დომენს ვყოფთ სამ ნაწილად სწორი ხაზებით, რომლებიც ნახატზე შავია. ჩვენ ვიანგარიშებთ ინტეგრაციის ახალ ზღვრებს ინვერსიული ფუნქციის მოძიებით. ინტეგრაციის სამი ახალი სფეროს ლიმიტები იქნება შემდეგი.

ამ ამოხსნის მიხედვით, ინტეგრაციის რიგის შეცვლის შემდეგ განმეორებითი ინტეგრალი უდრის სამი ინტეგრალის ჯამს:

სამი ინტეგრალის იგივე ჯამი ტოლი იქნება ორმაგი ინტეგრალის, რომელიც მცირდება ამ მაგალითის პირობებში მოცემულ განმეორებით ინტეგრალამდე.

და მაინც, ფორსმაჟორული გარემოებები ხშირად ერევა სტუდენტებს უკვე წინა საფეხურზე - ინტეგრაციის საზღვრების დაწესება. შფოთვა და დაბნეულობა არ არის რაიმე საფუძვლის გარეშე: თუ ინტეგრაციის რეგიონის ნაწილებად დაყოფა, ჩვეულებრივ, საკმარისია ნახატის კარგად დათვალიერება და განმეორებითი ინტეგრალის ამოხსნა - ინტეგრალების ცხრილი, მაშინ საჭიროა გარკვეული ტრენინგის გამოცდილება საზღვრების დაყენებაში. ინტეგრაციის. მოდით გადავხედოთ მაგალითს, რომელშიც ჩვენ გავამახვილებთ ყურადღებას მხოლოდ ინტეგრაციის საზღვრების დადგენაზე და - თითქმის ავტომატურად - რეგიონის დანაწევრებაზე და გამოვტოვებთ თავად გადაწყვეტას.

მაგალითი 11.იპოვეთ ორმაგი ინტეგრალის ინტეგრაციის საზღვრები, თუ ინტეგრაციის დომენი დმოცემულია შემდეგნაირად:

წ - 2x ≤ 0;
2 წ - x ≥ 0;
xy ≤ 2.

გამოსავალი. აშკარად (მით xდა წ„მინარევების გარეშე“) ინტეგრაციის რეგიონის შემზღუდველი ხაზები არ არის მითითებული. ვინაიდან X-სთვის ისინი ყველაზე ხშირად აღმოჩნდებიან სწორი ხაზები, რომლებიც ერთ წერტილში ეხება ზედა და ქვედა საზღვრებს, გამოხატული i-ით, მაშინ ჩვენ ზუსტად ამ გზას მივყვებით. უფრო მეტიც, ინტეგრაციის რიგის შეცვლისას ვიღებთ ინტეგრაციულ რეგიონს იგივე ფართობით. მოდით მოვაგვაროთ თამაშის უთანასწორობა და მივიღოთ:

წ ≤ 2x;
წ ≥ x/2;
წ ≤ 2/x.

ჩვენ ვქმნით შედეგად ხაზებს ნახაზზე. x-ზე ინტეგრაციის საზღვრები ნამდვილად არის ხაზები x= 0 და x= 2. მაგრამ ინტეგრაციის არეალი აღმოჩნდა წ-არასწორია, რადგან მისი ზედა ზღვარი არ შეიძლება დაზუსტდეს ერთი ხაზით წ = წ(x) .

შეიძლება სასარგებლო იყოს წაკითხვა: