რა არის პარალელოგრამის დიაგონალი. პარალელოგრამის დიაგონალების თვისებები. სრული გაკვეთილები - ცოდნის ჰიპერმარკეტი
პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები წყვილი პარალელურია. ეს განმარტება უკვე საკმარისია, ვინაიდან პარალელოგრამის დარჩენილი თვისებები მისგან გამომდინარეობს და დადასტურებულია თეორემების სახით.
პარალელოგრამის ძირითადი თვისებებია:
- პარალელოგრამი არის ამოზნექილი ოთხკუთხედი;
- პარალელოგრამს აქვს მოპირდაპირე გვერდები წყვილებში ტოლი;
- პარალელოგრამს აქვს მოპირდაპირე კუთხეები, რომლებიც ტოლია წყვილებში;
- პარალელოგრამის დიაგონალები იკვეთება გადაკვეთის წერტილით.
პარალელოგრამი - ამოზნექილი ოთხკუთხედი
ჯერ დავამტკიცოთ თეორემა, რომ პარალელოგრამი არის ამოზნექილი ოთხკუთხედი. მრავალკუთხედი ამოზნექილია, როდესაც მისი რომელი გვერდი გაჭიმულია სწორ ხაზამდე, მრავალკუთხედის ყველა სხვა მხარე იქნება ამ სწორი ხაზის იმავე მხარეს.
მიეცით პარალელოგრამი ABCD, რომელშიც AB არის მოპირდაპირე მხარე CD-სთვის, ხოლო BC არის მოპირდაპირე მხარე AD-სთვის. შემდეგ პარალელოგრამის განმარტებიდან გამომდინარეობს, რომ AB || CD, BC || ახ.წ.
პარალელურ სეგმენტებს არ აქვთ საერთო წერტილები, ისინი არ იკვეთებიან. ეს ნიშნავს, რომ CD დევს AB-ის ერთ მხარეს. ვინაიდან BC სეგმენტი აკავშირებს AB სეგმენტის B წერტილს CD სეგმენტის C წერტილთან, ხოლო AD სეგმენტი აკავშირებს სხვა AB და CD წერტილებს, BC და AD სეგმენტები ასევე დევს AB ხაზის იმავე მხარეს, სადაც დევს CD. ამრიგად, სამივე მხარე - CD, BC, AD - AB-ის ერთ მხარეს დევს.
ანალოგიურად, დადასტურებულია, რომ პარალელოგრამის სხვა გვერდებთან მიმართებაში, დანარჩენი სამი მხარე ერთ მხარეს დევს.
მოპირდაპირე მხარეები და კუთხეები ტოლია
პარალელოგრამის ერთ-ერთი თვისებაა ის პარალელოგრამში მოპირდაპირე გვერდები და მოპირდაპირე კუთხეები ტოლია. მაგალითად, თუ პარალელოგრამი მოცემულია ABCD, მაშინ მას აქვს AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. ეს თეორემა შემდეგნაირად არის დადასტურებული.
პარალელოგრამი არის ოთხკუთხედი. ასე რომ, მას აქვს ორი დიაგონალი. ვინაიდან პარალელოგრამი არის ამოზნექილი ოთხკუთხედი, ნებისმიერი მათგანი ყოფს მას ორ სამკუთხედად. განვიხილოთ სამკუთხედები ABC და ADC პარალელოგრამში ABCD, რომელიც მიღებულია AC დიაგონალის დახაზვით.
ამ სამკუთხედებს ერთი გვერდი აქვთ საერთო - AC. კუთხე BCA ტოლია CAD კუთხის, ისევე როგორც ვერტიკალები პარალელური BC და AD. კუთხეები BAC და ACD ასევე ტოლია, ისევე როგორც ვერტიკალური კუთხეები, როდესაც AB და CD პარალელურია. ამიტომ, ∆ABC = ∆ADC ორ კუთხით და მათ შორის მდებარე გვერდით.
ამ სამკუთხედებში AB გვერდი შეესაბამება CD მხარეს, ხოლო BC გვერდი შეესაბამება AD. ამიტომ, AB = CD და BC = AD.
კუთხე B შეესაბამება D კუთხეს, ანუ ∠B = ∠D. პარალელოგრამის A კუთხე არის ორი კუთხის ჯამი - ∠BAC და ∠CAD. კუთხე C ტოლი შედგება ∠BCA და ∠ACD-ისგან. ვინაიდან კუთხეების წყვილი ერთმანეთის ტოლია, მაშინ ∠A = ∠C.
ამრიგად, დადასტურდა, რომ პარალელოგრამში მოპირდაპირე გვერდები და კუთხეები ტოლია.
შუაზე გაჭრილი დიაგონალები
ვინაიდან პარალელოგრამი არის ამოზნექილი ოთხკუთხედი, მას აქვს ორი ორი დიაგონალი და ისინი იკვეთებიან. მიეცით პარალელოგრამი ABCD, მისი დიაგონალები AC და BD იკვეთება E წერტილში. განვიხილოთ მათ მიერ წარმოქმნილი სამკუთხედები ABE და CDE.
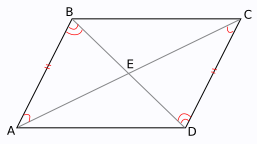
ამ სამკუთხედებს აქვთ AB და CD გვერდები პარალელოგრამის მოპირდაპირე გვერდების ტოლი. ABE კუთხე უდრის CDE კუთხს, რადგან ისინი მდებარეობენ პარალელურ ხაზებზე AB და CD. ამავე მიზეზით, ∠BAE = ∠DCE. აქედან გამომდინარე, ∆ABE = ∆CDE ორ კუთხით და მათ შორის მდებარე გვერდით.
თქვენ ასევე შეგიძლიათ შეამჩნიოთ, რომ AEB და CED კუთხეები ვერტიკალურია და, შესაბამისად, ერთმანეთის ტოლია.
ვინაიდან სამკუთხედები ABE და CDE ერთმანეთის ტოლია, ასე რომ, ყველა მათი შესაბამისი ელემენტი. პირველი სამკუთხედის AE გვერდი შეესაბამება მეორის CE მხარეს, ამიტომ AE = CE. ანალოგიურად, BE = DE. თანაბარი სეგმენტების თითოეული წყვილი ქმნის პარალელოგრამის დიაგონალს. ამრიგად, დადასტურებულია, რომ პარალელოგრამის დიაგონალები იკვეთება გადაკვეთის წერტილით.
ოთხკუთხედი, რომლის მოპირდაპირე გვერდები პარალელურია, არის პარალელოგრამი. დიაგონალები არის სწორი ხაზები, რომლებიც აკავშირებს საპირისპირო წვეროებს. მათი გადაკვეთის წერტილი არის სიმეტრიის ცენტრი. ზოგადად, პარალელოგრამს აქვს ორი დიაგონალი, D არის გრძელი და d არის მოკლე.
იპოვეთ პარალელოგრამის დიაგონალი კოსინუსების კანონის გამოყენებით
- α და β პარალელოგრამის კუთხეების კოსინუსების მნიშვნელობა.
D = √a^2 + b^2 - 2ab cosβ
d = √a^2 + b^2 + 2ab cosβ
D = √a^2 + b^2 + 2ab cosα
d = √a^2 + b^2 - 2ab cosα
იპოვეთ პარალელოგრამის დიაგონალი ერთი ცნობილი დიაგონალისა და გვერდების მიხედვით
ამ მეთოდის გამოსაყენებლად, თქვენ უნდა იცოდეთ:
- პარალელოგრამის a და b გვერდების სიგრძეები.
D = √2a^2 + 2b^2 - d^2
ამ მეთოდის გამოსაყენებლად, თქვენ უნდა იცოდეთ:
- პარალელოგრამის ფართობი.
- ერთ-ერთი დიაგონალის D ან d სიგრძე.
- კუთხე γ ან δ დიაგონალებს შორის.
D = 2S/d sinγ = 2S/d sinδ
d = 2S/D sinγ = 2S/D sinδ 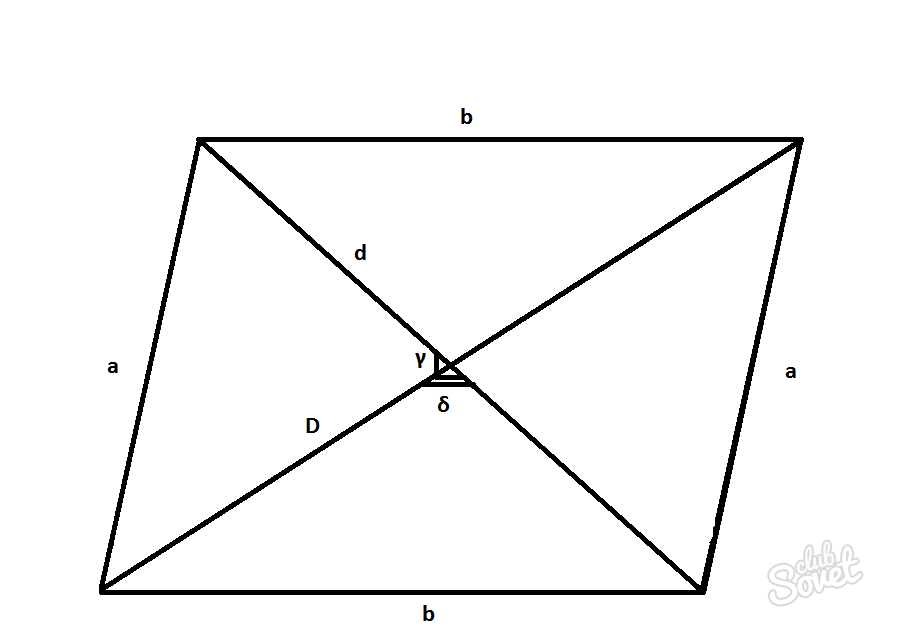
პარალელოგრამის დიაგონალის სიგრძის განსაზღვრის განსაკუთრებული შემთხვევაა კვადრატი
კვადრატი არის პარალელოგრამი, რომელშიც ყველა გვერდი ტოლია და კუთხეები 90°. დიაგონალების სიგრძე ამ შემთხვევაში ტოლი იქნება D=d და შეიძლება გამოითვალოს პითაგორას თეორემის გამოყენებით.
D=d=a*√2 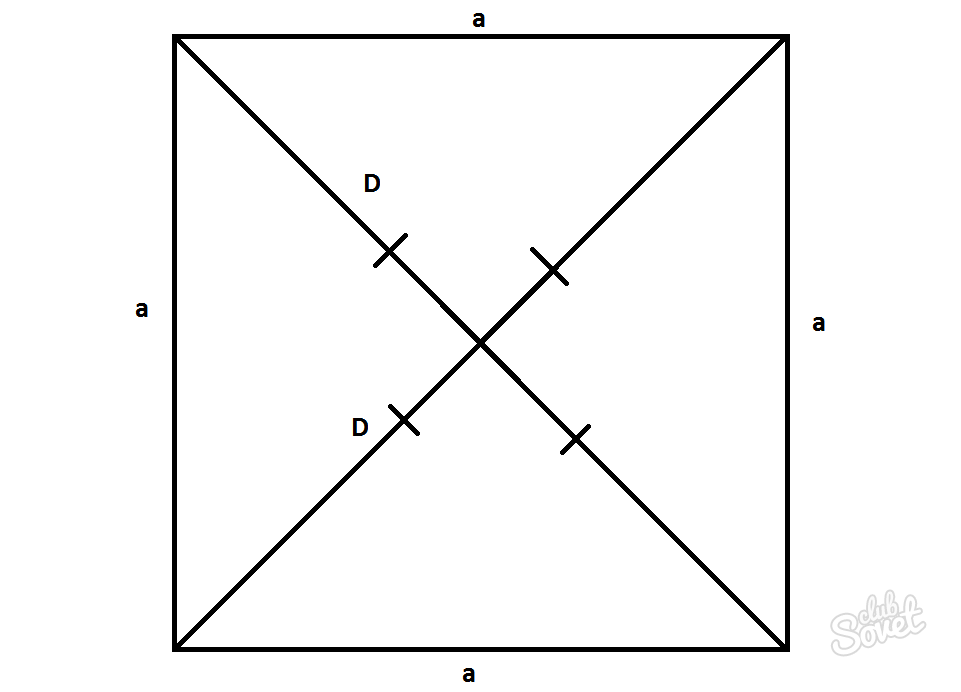
პარალელოგრამის დიაგონალის სიგრძის განსაზღვრის განსაკუთრებული შემთხვევაა მართკუთხედი
მართკუთხედი არის პარალელოგრამი, რომელშიც კუთხეები ტოლია და 90°-ის ტოლია. დიაგონალების სიგრძე ამ შემთხვევაში ტოლი იქნება D=d და შეიძლება გამოითვალოს პითაგორას თეორემის გამოყენებით.
D=d=√(a^2+b^2) 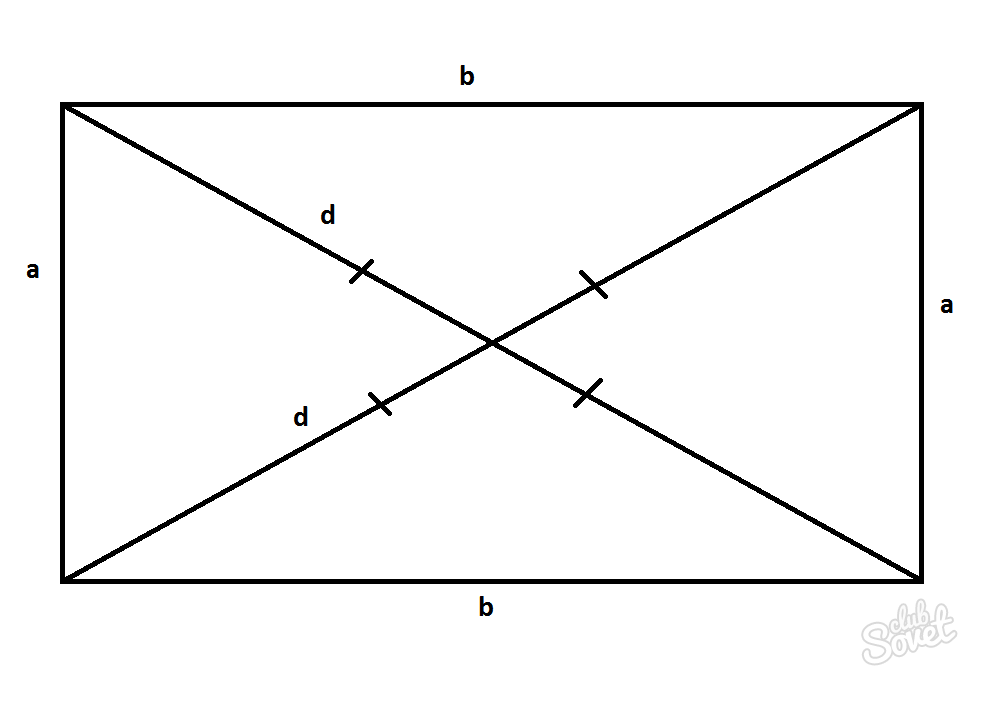
პარალელოგრამის თვისებები.
პარალელოგრამს საპირისპირო გვერდები ტოლი აქვს. პარალელოგრამს აქვს საპირისპირო კუთხეები.
პარალელოგრამის დიაგონალები იკვეთება და გადაკვეთის წერტილი შუაზე იყოფა (სურ. 96).
AB = CD, BC = AD, ?BAD = ?BCD, ?ABS = ?ADC, AO = OC, BO = OD.
პარალელოგრამის მახასიათებლები.
თუ ოთხკუთხედს აქვს ორი პარალელური და ტოლი გვერდი, მაშინ ის პარალელოგრამია (სურ. 97).
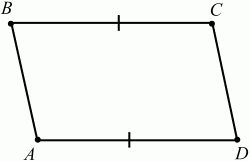
ძვ.წ.||ახ.წ.ძ.წ. ABCD არის პარალელოგრამი.
თუ ოთხკუთხედის დიაგონალები იკვეთება და გადაკვეთის წერტილი იყოფა შუაზე, მაშინ ეს ოთხკუთხედი პარალელოგრამია (სურ. 98).
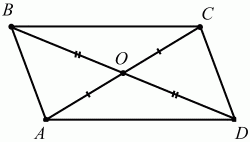
AO = OS, VO = OD? ABCD არის პარალელოგრამი.
მართკუთხედის თვისებები.
მართკუთხედს აქვს პარალელოგრამის ყველა თვისება (მართკუთხედს აქვს მოპირდაპირე გვერდები ტოლი; მართკუთხედს აქვს მოპირდაპირე კუთხეები ტოლი (90°); მართკუთხედის დიაგონალები იკვეთება და გადაკვეთის წერტილი იყოფა ნახევრად).
მართკუთხედის დიაგონალები ტოლია (სურ. 99):
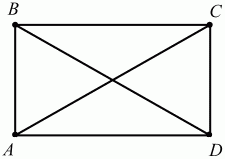
მართკუთხედის ნიშანი.
თუ პარალელოგრამს აქვს ყველა თანაბარი კუთხე, მაშინ ის მართკუთხედია.
რომბის თვისებები.
რომბისთვის დამახასიათებელია პარალელოგრამის ყველა თვისება (რომბისთვის მოპირდაპირე მხარეები ტოლია - ზოგადად, ყველა გვერდი ტოლია განსაზღვრებით; რომბისთვის საპირისპირო კუთხეები ტოლია; რომბის დიაგონალები იკვეთება და კვეთა წერტილი იყოფა ნახევრად).
რომბის დიაგონალები იკვეთება სწორი კუთხით.
რომბის დიაგონალები მისი კუთხეების ბისექტრებია (სურ. 100).
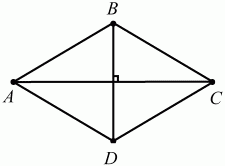
AC? BD, ?ABD = ?DBC = ?CDB = ?BDA, ?BAC = ?CAD = ?BCA = ?DCA.
რომბის ნიშანი.
თუ პარალელოგრამის დიაგონალები პერპენდიკულარულია, მაშინ ის არის რომბი.
კვადრატული თვისებები.
კვადრატს აქვს მართკუთხედის და რომბის თვისებები.
კვადრატული ნიშანი.
თუ მართკუთხედის დიაგონალები იკვეთება სწორი კუთხით, მაშინ ის არის კვადრატი.
საკუთრება შუა ხაზიტრაპეცია.
ტრაპეციის შუა ხაზი ფუძეების პარალელურია და მათი ნახევრად ჯამის ტოლია (სურ. 101).

წარწერიანი და შემოხაზული ოთხკუთხედების კრიტერიუმები.
თუ წრე შეიძლება შემოიფარგლოს ოთხკუთხედთან, მაშინ მისი საპირისპირო კუთხეების ჯამები უდრის თითოეულს 180 ° (ნახ. 102).
A + ?C = ?B + ?D = 180°.
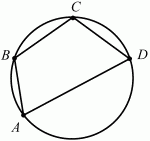
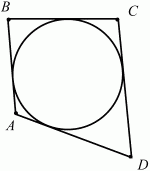
თუ წრე შეიძლება ჩაიწეროს ოთხკუთხედში, მაშინ მისი მოპირდაპირე გვერდების ჯამები ტოლია (სურ. 103).
AB + CD = AD + BC.
გაკვეთილის თემა
- პარალელოგრამის დიაგონალების თვისებები.
გაკვეთილის მიზნები
- გაეცანით ახალ განმარტებებს და გაიხსენეთ უკვე შესწავლილი.
- ჩამოაყალიბეთ და დაამტკიცეთ პარალელოგრამის დიაგონალების თვისება.
- ისწავლეთ ფორმების თვისებების გამოყენება ამოცანების ამოხსნაში.
- განმავითარებელი - მოსწავლეთა ყურადღების, გამძლეობის, შეუპოვრობის განვითარება, ლოგიკური აზროვნება, მათემატიკური მეტყველება.
- საგანმანათლებლო - გაკვეთილის საშუალებით, ერთმანეთის მიმართ ყურადღებიანი დამოკიდებულების ჩამოყალიბება, ამხანაგების მოსმენის უნარის, ურთიერთდახმარების, დამოუკიდებლობის განვითარება.
გაკვეთილის მიზნები
- შეამოწმეთ მოსწავლეთა პრობლემების გადაჭრის უნარი.
Გაკვეთილის გეგმა
- შესავალი.
- ადრე ნასწავლი მასალის გამეორება.
- პარალელოგრამი, მისი თვისებები და ნიშნები.
- დავალების მაგალითები.
- Თვითშემოწმება.
შესავალი
"მთავარი მეცნიერული აღმოჩენა გადაწყვეტს ძირითად პრობლემას, მაგრამ ნებისმიერი პრობლემის გადაწყვეტაში არის აღმოჩენის მარცვალი."
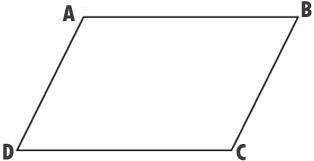
პარალელოგრამის საპირისპირო გვერდების თვისებები
პარალელოგრამს საპირისპირო გვერდები ტოლი აქვს.
მტკიცებულება.
ABCD იყოს მოცემული პარალელოგრამი. და მიეცი მას დიაგონალებიიკვეთება O წერტილში.
ვინაიდან Δ AOB = Δ COD სამკუთხედების ტოლობის პირველი ნიშნით (∠ AOB = ∠ COD, როგორც ვერტიკალურად, AO=OC, DO=OB, პარალელოგრამის დიაგონალების თვისებით), მაშინ AB=CD. ანალოგიურად, BOC და DOA სამკუთხედების ტოლობიდან გამომდინარეობს, რომ BC=DA. თეორემა დადასტურდა.
პარალელოგრამის საპირისპირო კუთხეების თვისება
პარალელოგრამს აქვს საპირისპირო კუთხეები.
მტკიცებულება.
დაე, ABCD იყოს მოცემული პარალელოგრამი. და მოდით, მისი დიაგონალები იკვეთოს O წერტილში.
პარალელოგრამის საპირისპირო გვერდების თვისებებიდან დადასტურებული თეორემაში Δ ABC = Δ CDA სამ მხარეს (AB=CD, BC=DA დადასტურებულიდან, AC ზოგადია). სამკუთხედების ტოლობიდან გამომდინარეობს, რომ ∠ABC = ∠CDA.
ასევე დადასტურებულია, რომ ∠ DAB = ∠ BCD, რომელიც გამომდინარეობს ∠ ABD = ∠ CDB-დან. თეორემა დადასტურდა.
პარალელოგრამის დიაგონალების თვისება
პარალელოგრამის დიაგონალები იკვეთება და გადაკვეთის წერტილი ორად იკვეთება.
მტკიცებულება.
ABCD იყოს მოცემული პარალელოგრამი. დავხატოთ AC დიაგონალი. მასზე ვნიშნავთ შუა O-ს, DO სეგმენტის გაგრძელებაზე ვდებთ DO-ს ტოლი OB 1 სეგმენტს.
წინა თეორემით AB 1 CD არის პარალელოგრამი. მაშასადამე, ხაზი AB 1 არის DC-ის პარალელურად. მაგრამ A წერტილის გავლით DC-ის პარალელურად მხოლოდ ერთი ხაზის გაყვანა შეიძლება. აქედან გამომდინარე, ხაზი AB 1 ემთხვევა AB ხაზს.
ასევე დადასტურებულია, რომ ძვ.წ 1 ემთხვევა ძვ.წ. ასე რომ, C წერტილი ემთხვევა C 1-ს. პარალელოგრამი ABCD ემთხვევა პარალელოგრამს AB 1 CD. ამრიგად, პარალელოგრამის დიაგონალები იკვეთება და გადაკვეთის წერტილი ორად იკვეთება. თეორემა დადასტურდა.
ჩვეულებრივი სკოლების სახელმძღვანელოებში (მაგალითად, პოგორელოვში) ასეა დადასტურებული: დიაგონალები ყოფენ პარალელოგრამს 4 სამკუთხედად. განვიხილოთ ერთი წყვილი და გაარკვიეთ - ისინი ტოლია: მათი ფუძეები მოპირდაპირე გვერდებია, მის მიმდებარედ შესაბამისი კუთხეები ტოლია, როგორც ვერტიკალური პარალელური ხაზებით. ანუ დიაგონალების სეგმენტები წყვილად ტოლია. ყველა.
Სულ ეს არის?
ზემოთ დადასტურდა, რომ გადაკვეთის წერტილი ყოფს დიაგონალებს - თუ ის არსებობს. ზემოაღნიშნული მსჯელობა არანაირად არ ადასტურებს მის არსებობას. ანუ თეორემის ნაწილი „პარალელოგრამის დიაგონალების იკვეთება“ რჩება დაუმტკიცებელი.
სასაცილოა, რამდენად რთულია ამ ნაწილის დამტკიცება. სხვათა შორის, ეს უფრო ზოგადი შედეგიდან გამომდინარეობს: ნებისმიერი ამოზნექილი ოთხკუთხედისთვის დიაგონალები იკვეთება, ნებისმიერი არაამოზნექილისთვის - არა.
გვერდის გასწვრივ სამკუთხედების და მის მიმდებარე ორი კუთხის ტოლობის შესახებ (სამკუთხედების ტოლობის მეორე ნიშანი) და სხვა.
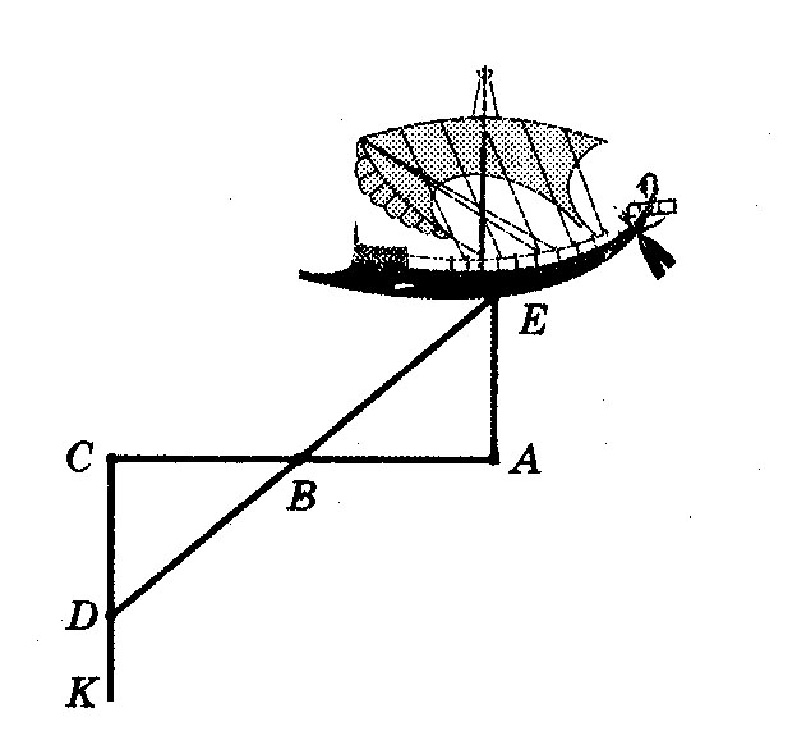
თეორემა გვერდის გასწვრივ ორი სამკუთხედის და მის მიმდებარე ორი კუთხის ტოლობის შესახებ, თალესმა იპოვა მნიშვნელოვანი პრაქტიკული გამოყენება. მილეტის ნავსადგურში აშენდა დიაპაზონი, რომელიც განსაზღვრავს მანძილს ზღვაზე გემამდე. იგი შედგებოდა სამი ამოძრავებული სამაგრი A, B და C (AB = BC) და მონიშნული სწორი ხაზი SK, პერპენდიკულარული CA. როდესაც გემი გამოჩნდა SC სწორ ხაზზე, აღმოჩნდა D წერტილი ისეთი, რომ D, .B და E წერტილები იმავე სწორ ხაზზე იყო. როგორც ნახატიდან ირკვევა, CD მანძილი ადგილზე არის სასურველი მანძილი გემამდე.
კითხვები
- კვადრატის დიაგონალები იკვეთება გადაკვეთის წერტილით?
- პარალელოგრამის დიაგონალები ტოლია?
- პარალელოგრამის საპირისპირო კუთხეები ტოლია?
- რა არის პარალელოგრამის განმარტება?
- პარალელოგრამის რამდენი თვისებაა?
- შეიძლება რომბი იყოს პარალელოგრამი?
გამოყენებული წყაროების სია
- კუზნეცოვი A.V., მათემატიკის მასწავლებელი (5-9 კლასები), კიევი
- „ერთიანი სახელმწიფო გამოცდა 2006წ. მათემატიკა. საგანმანათლებლო და სასწავლო მასალები სტუდენტების მოსამზადებლად / Rosobrnadzor, ISOP - M .: Intellect-Center, 2006 "
- Mazur K. I. "მ.ი. სკანავის რედაქტორული კრებულის ძირითადი საკონკურსო ამოცანების ამოხსნა მათემატიკაში"
- ლ.
გაკვეთილზე მუშაობა
კუზნეცოვი A.V.
Poturnak S.A.
ევგენი პეტროვი
თქვენ შეგიძლიათ დასვათ შეკითხვა თანამედროვე განათლების შესახებ, გამოხატოთ აზრი ან გადაწყვიტოთ გადაუდებელი პრობლემა განათლების ფორუმისადაც ახალი აზრისა და მოქმედების საგანმანათლებლო საბჭო იკრიბება საერთაშორისო დონეზე. რომელმაც შექმნა ბლოგი,თქვენ არა მხოლოდ გააუმჯობესებთ კომპეტენტური მასწავლებლის სტატუსს, არამედ მნიშვნელოვან წვლილს შეიტანთ მომავლის სკოლის განვითარებაში. განათლების ლიდერთა გილდიაკარს უხსნის უმაღლესი რანგის სპეციალისტებს და გიწვევთ თანამშრომლობისთვის მსოფლიოში საუკეთესო სკოლების შექმნის მიმართულებით.
შეიძლება სასარგებლო იყოს წაკითხვა:
- წმიდა მიროს მატარებელი ქალების დღე;
- ვნების მატარებელი ევგენი ბოტკინი მოწამე ევგენი ბოტკინი;
- სასულიერო რეპი: ჩუვაშური "ოხლობისტინი" ასწავლის მოზარდებს სიყვარულსა და თავმდაბლობას რეჩიტატივით;
- ეპარქიული მისიონერული კურსები: ლექცია პროტოდიაკონის მისიონერულ მოღვაწეობაზე ა;
- როგორ გავიგოთ, რა მოსწონს მორიელს;
- Zombie Apocalypse ონლაინ მეგობრებთან ერთად;
- ონლაინ თამაშები Zombie Apocalypse თამაში;
- პრობლემები ფიფას თამაშის დაწყებასთან დაკავშირებით;