Osnovne lastnosti dvojnega integrala. Naloga dvojnega integrala definicija glavnih lastnosti dvojnega integrala Dvojni integral osnovni pojmi in definicije
Osnovne lastnosti dvojnega integrala
Lastnosti dvojnega integrala (in njihove izpeljave) so podobne ustreznim lastnostim enojnega določenega integrala.
1°. Aditivnost. Če funkcija f(x, l) je integrabilen v domeni D in če območje D z uporabo krivulje G območja nič je razdeljen na dve povezani regiji brez skupnih notranjih točk D 1 in D 2, nato funkcijo f(x, l) je integrabilen v vsaki od domen D 1 in D 2 in
2°. Linearna lastnost. Če funkcije f(x, l) In g(x, l) so integrabilni v domeni D, A α in β so poljubna realna števila, potem je funkcija [ α · f(x, l) + β · g(x, l)] je tudi integrabilen v domeni D, in
3°. Če funkcije f(x, l) In g(x, l) so integrabilni v domeni D, potem je tudi produkt teh funkcij integrabilen v D.
4°. Če funkcije f(x, l) In g(x, l) oba sta integrabilna v domeni D in povsod na tem območju f(x, l) ≤ g(x, l), to
5°. Če funkcija f(x, l) je integrabilen v domeni D, potem funkcija | f(x, l)| integracijski v območju D, in
(Seveda iz integrabilnosti | f(x, l)| V D integrabilnost ne sledi f(x, l) V D.)
6°. Izrek o srednji vrednosti. Če obe funkciji f(x, l) In g(x, l) so integrabilni v domeni D, funkcija g(x, l) je nenegativen (nepozitiven) povsod v tej regiji, M in m- natančne zgornje in natančne spodnje meje funkcije f(x, l) na območju D, potem je tu številka μ , ki izpolnjuje neenakost m ≤ μ ≤ M in tako, da formula
Problem, ki vodi do koncepta dvojnega integrala Definicija dvojnega integrala Osnovne lastnosti dvojnega integrala Območje ravnega območja Redukcija dvojnega integrala na iteriranega Sprememba spremenljivk v dvojnem integralu Območni element v krivuljnih koordinatah Jacobian in njegov geometrijski pomen Sprememba spremenljivk formula v dvojnem integralu Dvojni integral v polarnih koordinatah


















Problem, ki vodi do koncepta dvojnega integrala. Definicija dvojnega integrala. Do pojma dvojnega integrala pridemo z reševanjem določenega problema izračuna prostornine valjastega telesa. Valjasto telo je telo, ki ga omejujejo ravnina xOy, neka ploskev in valjasta ploskev, katere generatorji so vzporedni z osjo (glej sliko 1). Območje D spremembe spremenljivk x in y imenujemo osnova valjastega telesa. Pri določanju prostornine telesa bomo izhajali iz dveh načel: !) če je telo razdeljeno na dele, potem je njegova prostornina enaka vsoti prostornin vseh delov (lastnost aditivnosti); 2) prostornina ravnega valja, ki ga omejuje ravnina z = const, vzporedna z ravnino xOy, je enaka osnovni površini, pomnoženi z višino. V nadaljevanju bomo domnevali, da je domena D povezana (sestavljena iz enega kosa), kvadrirana (tj. ima ploščino) in omejena (tj. nahaja se znotraj nekega kroga s središčem v izhodišču). Naj bo zvezna funkcija točke P(x, y) v domeni povsod v domeni Z>, tj. da obravnavana cilindrična površina v celoti leži nad ravnino xOy. Prostornino valjastega telesa označimo z V. Področje D - osnovo valjastega telesa razdelimo na določeno število n nesekajočih se kvadratov poljubne oblike; imenovali jih bomo delne regije. Po oštevilčenju delnih regij v določenem vrstnem redu, območij - skozi oz. Premer delnega območja Dk imenujemo količina Problem, ki vodi do koncepta dvojnega integrala Definicija dvojnega integrala Osnovne lastnosti dvojnega integrala Površina ravnega območja Redukcija dvojnega integrala na iteriranega Sprememba spremenljivk v dvojnem integralu Ploščinski element v krivočrtnih koordinatah Jacobian in njegov geometrijski pomen Sprememba spremenljivk Formula v dvojnem integralu Dvojni integral v polarnih koordinatah, kjer simbol p(P; Q) označuje razdaljo med točkama P in Q. Naj d označuje največji izmed premerov delnih območij Dk (k = 1,2,...,n). Skozi mejo vsakega delnega območja narišimo valjasto ploskev z generatorji, vzporednimi z osjo Oz. Posledično bo valjasto telo razdeljeno na n delnih valjastih teles. Zamenjajmo k-to delno telo z ravnim valjem z enako osnovo in višino, ki je enaka nastavku neke točke zamenjane ploskve (slika 2). Prostornina takega valja je tam, kjer je točka območje območja Dk. Ko naredimo opisane konstrukcije za vsako delno cilindrično telo, dobimo n-stopenjsko telo, katerega prostornina (o) Intuitivno je jasno, da Vn izraža želeni volumen V tem natančneje, čim manjše so dimenzije delnih območij Dk . Sprejmemo, da je prostornina V cilindričnega telesa enaka meji, h kateri stremi prostornina (1) n-stopenjskega telesa, ko največji premer d delnih območij Dk stremi k nič n. Meja seveda ne sme biti odvisna od vrste razdelitve področja D na delna področja Dk in od izbire točk Pk v delnih področjih. Naj bo f(x, y) poljubna funkcija, definirana v domeni D. Vsoto n (1) imenujemo integralna vsota za funkcijo f(x)y) nad domeno D, ki ustreza dani razdelitvi te domene na n delnih domen in podana izbira točk ®*,!/*) na delnih domenah Dk. Opredelitev. Če za d - * 0 obstaja meja integralnih vsot n, ki ni odvisna od metode razdelitve domene D na delne domene niti od izbire točk Pk v delnih domenah, potem jo imenujemo dvojni integral funkcija f(P) (ali f(x, y )) nad domeno D in je označena s simbolom ALI Torej, (2) Funkcija f(x, y) sama se imenuje integrabilna v domeni D (f( P) je integrand, f(P) dS je integrand, dS je diferencial (ali element) površine, območje D je območje integracije; točka P (®, y) je spremenljivka fina integracija) . ,.. Če se vrnemo k valjastemu telesu, sklepamo: prostornina valjastega telesa, ki ga omejujejo ravnina xOy, površina in valjasta površina z generatorji, vzporednimi z osjo Oz, je enaka dvojnemu integralu funkcije f(x , y) nad območjem D, ki je osnova cilindričnega telesa. / ALI Tukaj je dx dy površinski element v kartezičnih koordinatah. To je geometrijski pomen dvojnega integrala nenegativne funkcije. Če potem volumen If v območju D funkcije f (P) zavzame pozitivne in negativne vrednosti, potem integral predstavlja algebraično vsoto prostornin tistih delov telesa, ki se nahajajo nad ravnino xOy (vzeto z znak “+”) in tiste dele telesa, ki se nahajajo pod ravnino xOy (vzeto z znakom “-”). Do sestavljanja vsot oblike (1) za funkcijo dveh neodvisnih spremenljivk in kasnejšega prehoda do limite vodijo različni problemi in ne le problem prostornine valjastega telesa. Formulirajmo zadostne pogoje za integrabilnost. Izrek 1. Vsaka funkcija y), zvezna v omejeni zaprti domeni D, je v tej domeni integrabilna. Zahteva po kontinuiteti integranda je pogosto preveč omejevalna. Za aplikacije je pomemben naslednji izrek, ki zagotavlja obstoj dvojnega integrala za določen razred diskontinuiranih funkcij. Rekli bomo, da ima neka množica točk v ravnini ploščino nič, če jo lahko zapremo v mnogokotnik poljubno majhne ploščine. Izrek 2. Če je funkcija f(x, y) omejena v zaprti omejeni domeni D in zvezna povsod v D, razen v neki množici točk območja nič, potem je ta funkcija integrabilna v domeni D. §2. Osnovne lastnosti dvojnega integrala Dvojni integrali imajo številne lastnosti, podobne tistim, ki jih ima določen integral za funkcije ene neodvisne spremenljivke. 2.1. Linearna lastnost Če sta funkciji a) integrabilni v domeni D in sta a in p poljubni realni števili, potem je tudi funkcija af) integrabilna v domeni D in o) 2.2. Integracija neenakosti Če so funkcije) integrabilne v domeni D in povsod v tej domeni, potem (2), tj. neenakosti so lahko integrirane. Zlasti z integracijo očitnih neenakosti dobimo površino ravnega območja Območje ravnega območja D je enako dvojnemu integralu nad tem območjem funkcije, ki je identično enaka eni. Dejansko ima integralna vsota za funkcijo /(P) = 1 v domeni D obliko in je za vsako razdelitev domene D na delne domene Dt enaka njeni površini S. Toda potem je meja te vsote, tj. , dvojni integral, je enaka površini S domen D: ali, kar je enako, (3) 2.4. Ocena integrala. Naj bo funkcija /(P) zvezna v omejenem zaprtem območju D, naj bosta M in mn največja in najmanjša vrednost /(P) v območju D in naj bo 5 njegovo območje. Potem (4) 2,5. Aditivnost: Če je funkcija /(P) integrabilna v domeni D in je domena Z) razdeljena na dve domeni D\ in Di brez skupnih notranjih točk, potem je /(P) integrabilna na vsaki od domen D\ in Di in (5) 2.6. Izrek o srednji vrednosti Izrek 3 (o srednji vrednosti). Če je funkcija /(P) zvezna v zaprtem omejenem območju D, potem obstaja vsaj ena točka Pc področja D, tako da velja formula u, kjer je S območje območja D področja D, potem prevzame v D svojo največjo vrednost M in svojo najmanjšo vrednost m. Z lastnostjo 4 o oceni integrala P) v domeni D zavzame na neki točki Pc G D vrednost, ki je enaka temu številu, od koder je S vrednost f(Pc), določena s formulo (7), se imenuje srednja vrednost funkcije f(P) v domeni D. vrednost Če je v območju D funkcija /(P) ^ O, potem formula (6) pomeni, da obstaja raven valj z osnovo D (katerega ploščina je 5) in višino H = /(Pc), katerega prostornina je enaka prostornini valjastega telesa (sl. 3). § 3. Redukcija dvojnega integrala na iterirani integral Eden od učinkovitih načinov za izračun dvojnega integrala je redukcija na iterirani integral. 3.1. Primer pravokotnika Naj bo območje D zaprt pravokotnik Π s stranicami, vzporednimi s koordinatnimi osemi. Naj bo funkcija f(x, y) zvezna v pravokotniku P. Dvojni integral lahko interpretiramo kot (algebraično) prostornino valjastega telesa z osnovo P, ki jo omejuje ploskev. Razmislimo o ustreznem valjastem telesu. Narišimo ravnino, pravokotno na os Oy (slika 4). Ta ravnina reže valjasto telo vzdolž krivuljnega trapeza, ki je od zgoraj omejen z ravno črto z, ki je opisana z enačbami. Ploščina trapeza ABB\A\ je izražena z integralom, kjer se integracija izvaja po x, in yo - drugi argument integranda - se obravnava kot konstanta). Vrednost integrala (1) je odvisna od izbire vrednosti y0. Postavimo (2) Izraz (2) podaja površino prečnega prereza valjastih teles a kot funkcijo y. Zato lahko prostornino cilindričnega telesa izračunamo s formulo. Po drugi strani pa je ta prostornina izražena z dvojnim integralom funkcije /(x, y) nad pravokotnikom P. Zato zamenjava S(y) z njegovim izraz (2), dobimo Problem, ki vodi do koncepta dvojnega integrala Definicija dvojnega integrala Osnovne lastnosti dvojnega integrala Območje ravnega območja Redukcija dvojnega integrala na iteriranega Sprememba spremenljivk v dvojnem integral Ploščinski element v krivočrtnih koordinatah Jacobian in njegov geometrijski pomen Sprememba spremenljivk Formula v dvojnem integralu Dvojni integral v polarnih koordinatah Zadnjo relacijo običajno zapišemo takole. Prostornino valjastega telesa lahko najdemo tudi s presečnimi površinami ravnini x = x0. To vodi do formule (4) Vsak od izrazov na desni strani formul (3) in (4) vsebuje dve zaporedni operaciji navadne integracije funkcije f(x, y). Imenujemo jih iterirani integrali funkcije f(x, y) nad področjem Π. Če je f(x, y) zvezen v zaprtem pravokotniku Π, je prehod na iterirane integrale vedno možen in (5) tj. vrednosti ponavljajočih se integralov zvezne funkcije /(x, y) niso odvisne od vrstnega reda integracije. Primer 1. Poiščite dvojni integral funkcije nad ploščino Imamo (glej sliko 5): 3.2. Primer poljubne domene Predpostavimo zdaj, da je integracijska domena poljubno omejena kvadrirana zaprta domena D na ravnini xOy, ki izpolnjuje naslednji pogoj: vsaka premica, vzporedna z osjo Oy, seka mejo domene D pri največ dveh točkah ali vzdolž celega segmenta (sl. 6 a). Območje D zapremo znotraj pravokotnika, kot je prikazano na sl. 66. Odsek [a, 6] je pravokotna projekcija območja D na os Oxy, odsek [c, dj pa je pravokotna projekcija območja D na os Oy. S točkama A in C je meja območja D razdeljena na dve krivulji ABC in AEC. Vsaka od teh krivulj seka s poljubno ravno črto, vzporedno z osjo Oy, v največ eni točki. Zato lahko njihove enačbe zapišemo v obliki, ki je dovoljena za y: Naj bo f(x, y) neka zvezna funkcija v domeni D. Prerežemo obravnavano valjasto telo z ravnino. V odseku dobimo krivolinijski trapez PQMN (slika 7), katerega območje je izraženo z navadnim integralom funkcije / (x, y), ki se obravnava kot funkcija ene spremenljivke y. V tem primeru se spremenljivka y spremeni iz ordinate točke P v ordinato točke Q\ točka P je *!-ka "vhod" premice x = const (v ravnini) v območje - točko njenega "izstopa" iz te regije. Ker obstaja enačba za krivuljo ABC in za krivuljo, sta ti ordinati enaki, če vzamemo x. Zato nam integral poda izraz za površino ravnega odseka valjastega telesa kot funkcijo položaja sekantne ravnine x = const. Prostornina celotnega telesa bo enaka integralu tega izraza po w v intervalu spremembe. Tako zlasti za območje S območja D dobimo. Predpostavimo, da vsaka črta seka mejo območja D v največ dveh točkah P in Q, katerih abscisi sta enaki (ali vzdolž cel segment) (slika 8). S podobnim sklepanjem pridemo do formule, ki prav tako zmanjša izračun dvojnega integrala na ponovljenega. Zgled 2. Izračunaj dvojni integral funkcije po ploskvi D. omejena s premicami ^ Prvi način. Predstavimo območje integracije D. Premica y = x in parabola y = x2 se sekata v točkah). To pomeni, da se x spreminja v 8 mejah od 0. Vsaka premica x = const) seka mejo območja v največ dveh točkah. Zato velja formula (8): Druga metoda (slika 10). Uporaba formule (10). dobimo enak rezultat: Primer 3. Izračunaj prostornino telesa, ki ga omejuje ploskev seka ravnino xOy vzdolž elipse s polosemi zaradi simetrije tega telesa glede na koordinatni ravnini xOx in y, dobimo: Opomba. Če je domena D taka, da nekatere premice (bodisi pravokotne bodisi vodoravne) sekajo njeno mejo v več kot dveh točkah, potem je za izračun dvojnega integrala nad domeno D potrebno le-to na primeren način razdeliti na dele, da ponoviti integracijo integralov v dele in sešteti rezultate . Primer 4. Izračunajte dvojni integral po ploskvi D, zaprti med dvema kvadratoma s središčema ter v izhodišču in stranicah, vzporednih s koordinatnimi osemi, če je stranica notranjega kvadrata 2, zunanjega pa 4. je zvezen kot v velikem kvadratu Q, katerega stranica je 4, in v malem kvadratu R., katerega stranica je enaka 2 (slika 12). Po izreku 1 integrali funkcije e*** po označenih kvadratih obstajajo, tako da je vrednost želenega integrala §4. Sprememba spremenljivk v dvojnem integralu 4.1. Pojem krivuljnih koordinat točke Naj bo v domeni D* ravnine uOv podan par funkcij, za katere bomo menili, da so v tem področju zvezne in imajo zvezne parcialne odvode. Na podlagi enačbe (1) vsaka točka M*(x, v) območja D* ustreza eni določeni točki M(x, y) v ravnini xOy in tako točkam območja D* ustreza določena množica D točk (x, y) v ravnini xy (slika 13). V tem primeru naj bi funkcije (1) preslikale območje D4 na množico D. Recimo, da različne točke (u, v) ustrezajo različnim točkam (x, y). To je enakovredno edinstveni rešljivosti enačb (1) glede na u, v: V tem primeru se preslikava imenuje ena proti ena preslikava domene D* na domeno D. Pri taki transformaciji je katera koli zvezna krivulja L*, ki leži v domeni D*, bo prešla v zvezno krivuljo L, ki leži v območju D. Če sta funkciji q(x) y) in h(x, y) prav tako zvezni, potem vsaka zvezna črta LCD, ki uporablja transformacijo (2) bo šlo čez neprekinjeno črto L* C D*. Za dani par W, Vo vrednosti spremenljivk u, v iz območja D* je mogoče enolično določiti ne le položaj točke M*(u<)> Vq) v samem področju ξ)*, temveč položaj ustrezne točke M(xo, yo) v področju D, xo = 4>(o, v0), 3/0 = o, vo). To daje razlog, da štejemo številki u, v kot nekaj novih koordinat točke D območja M na ravnini xOy. Imenujemo jih krivočrtne koordinate točke M. Množico točk v območju D, za katere ena od koordinat ostane konstantna, imenujemo koordinatna premica. Če v formuli (1) predpostavimo, da je u = vq, dobimo parametrične enačbe koordinatne premice, pri čemer vlogo parametra igra spremenljivka u. Če koordinati v dodelimo različne (zanjo možne) konstantne vrednosti, dobimo družino koordinatnih premic (v = const) na ravnini xOy. Podobno dobimo drugo družino koordinatnih premic (u = const). Če med območji D* in D obstaja korespondenca ena proti ena, se različne koordinatne črte iste družine med seboj ne sekajo in ena premica iz vsake družine poteka skozi katero koli točko regije D. Mreža krivuljnih koordinatnih črt na ravnini xOp je podoba pravokotne mreže na ravnini uOv (glej sliko 13). 4.2. Element ploščine v krivuljnih koordinatah. Jacobian in njegov geometrijski pomen Izločimo v območju D* na ravnini Uo*V majhen pravokotnik P*P?P$Pl s stranicami, vzporednimi s koordinatnima osema 0*u in O"v ter dolžinami strani Au in Av (za določnost predpostavimo, da je A ) oziroma (sl. 14 a). Njegovo območje Pravokotnik se spremeni v krivolinijski štirikotnik * v območju D (sl. 146). Če imajo oglišča P) koordinate, potem , glede na formule (1) imajo ustrezna oglišča Pi koordinate), Z uporabo Taylorjeve formule za funkcijo dveh spremenljivk in se omejimo na člene prvega reda / pc glede na Au in Av, dobimo naslednje približno vrednosti koordinat za oglišča štirikotnika, kjer so funkcije, vse njihove odvodnice izračunane v točki vrstni red štirikotnik P\PiPiPa je paralelogram. To izhaja iz dejstva, da je potem ploščino DS štirikotnika mogoče približno izraziti glede na dolžino vektorskega produkta, gram Definicija dvojnega integrala Osnovne lastnosti dvojnega integrala Območje ravnega območja Redukcija dvojnega integrala na iterirano Sprememba spremenljivk v dvojnem integralu Območni element v krivuljnih koordinatah Jacobian in njegov geometrijski pomen Sprememba spremenljivk formula v dvojni integral Dvojni integral v polarnih koordinatah Determinanta Iz formul (7) in (8) videa, da ima absolutna vrednost Jacobiana vlogo lokalnega faktorja raztezanja območja D" (v dani točki (tx, v)) ko je preslikana na območje D z uporabo transformacijskih formul (1). 4.3. Formula za spremembo spremenljivk v dvojnem integralu Naj zvezne funkcije izvedejo eno proti ena preslikavo domene D* na D in imajo zvezne delne odvode prvega reda. Naj bo podana zvezna funkcija v domeni D na ravnini xOy. Vsaki vrednosti funkcije) v domeni D ustreza enaka vrednost funkcije r = v domeni D, kjer (u, v) in (x , y) tako, da vrednosti funkcij v njih sovpadajo, in sestavimo integralne vsote za funkcije z = /(x, y) in v) po domenah D in D*. Dobimo jakobian (9) do meje, ko se največji premer d* delnih območij D\ nagiba k nič (zaradi kontinuitete preslikave (I) bo težil tudi največji od premerov d delnih območij v D na nič), imamo kjer je pogoj J Ф 0 pogoj Izrek 4. Da bi transformirali dvojni integral, podan v kartezičnih koordinatah, v dvojni integral v krivuljnih koordinatah, je treba v integrandu f(x, y) zamenjati s spremenljivkami s oziroma y skozi in površinski element dx dy - njegov izraz v krivuljnih koordinatah: Primer. Poiščite območje figure, omejene s hiperbolami m. Iskanje površine označene figure se zmanjša na izračun dvojnega integrala nad območjem O. Uvedemo nove, krivulje koordinate u in o s formulami To pomeni, da smo v ravnini uOv dobili pravokotnik (sl. 156) - lik, ki je enostavnejši od danega lika D. Izrazimo x in y iz relacij (11) skozi u in t>: sl. 15 Nato Dvojni integral v polarnem koordinate Izračun dvojnega integrala pogosto poenostavljen z zamenjavo pravokotnih koordinat x in y s polarnimi koordinatami po formulah Ploščinski element v polarnih koordinatah ima obliko in formulo za prehod iz integrala v kartezičnih koordinatah v integral v polarnih koordinatah lahko zapišemo na naslednji način: V tem primeru (13) Ploščinski element v polarnih koordinatah lahko dobimo iz geometrijskih premislekov (glej sliko 16). Območje območja, zasenčenega na sliki A \u003d pl. sektorji. sektorji Če zavržemo infinitezimalno vrednost višjega reda, dobimo in sprejmemo kot površinski element v polarnih koordinatah. Torej, če želite pretvoriti dvojni integral v kartezičnih koordinatah v dvojni integral v polarnih koordinatah, morate zamenjati a: in y v integrandu s p costp oziroma psiny ter nadomestiti element ploščine v kartezičnih koordinatah dx dy s ploščino element v polarnih koordinatah p dp dip. Lotimo se zdaj izračuna dvojnega integrala v polarnih koordinatah. Tako kot v primeru pravokotnih kartezičnih koordinat se izračun integrala v polarnih koordinatah izvede z redukcijo na iterirani integral. Oglejmo si najprej primer, ko leži pol O zunaj danega območja D. Naj ima območje D to lastnost, da vsak žarek, ki izhaja iz pola (koordinatna premica y, seka njegovo mejo največ v dveh točkah ali vzdolž celega odseka ( Slika 17) Upoštevajte, da so skrajne vrednosti i polarnega kota meje zunanje integracije. Žarek q> = poteka skozi točko A konture območja D, žarek pa skozi točko B. točke Aw B delijo konturo območja D na dva dela: ACB in AFB Naj sta njuni polarni enačbi, kjer) sta enovredni zvezni funkciji, ki izpolnjujeta pogoj Funkcije so limiti notranje integracije. Če preidemo na iterirane integrale, dobimo naslednjo formulo. Zlasti za območje S domene D za F(p, r 1 dobimo mejo območja samo na eni točki ali vzdolž celotnega segmenta (slika 18) Naj - enačba meje območja v polarnih koordinatah Nato Slika 18 Primer Izračunajte integral, kjer je območje četrtina enotskega kroga, ki se nahaja v prvem kvadrantu. Preidimo na polarne koordinate Potem je območje integracije a pravokotnik Transformirani integral / je enostavno izračunati: r Opomba: Če je Jacobian različen od nič v domeni D, potem je preslikava v neki soseski vsake točke te domene ena proti ena, vendar se lahko zgodi, da preslikava celotne domene ni ena proti ena. Oglejmo si preslikavo, ki jo definirajo funkcije. Jacobian teh funkcij je enak in je zato povsod različen od nič. Kljub temu, ker dobimo, torej ta preslikava ni ena proti ena. Po drugi strani pa, če Jacobian preslikave na neki točki izgine, potem se kljub temu lahko izkaže, da je preslikava v okolici te točke ena proti ena. Na primer, za preslikavo, ki jo definirajo funkcije, je Jacobian enak nič in at, vendar je preslikava ena proti ena. Obratno preslikavo definirajo funkcije
1.1 Definicija dvojnega integrala





1.2 Lastnosti dvojnega integrala
Lastnosti dvojnega integrala (in njihove izpeljave) so podobne ustreznim lastnostim enojnega določenega integrala.
1°. Aditivnost. Če je funkcija f(x, y) integrabilna v domeni D in če je domena D razdeljena s krivuljo Γ površine nič na dve povezani domeni D 1 in D 2 brez skupnih notranjih točk, potem je funkcija f(x, y) je integrabilen v vsaki od regij D 1 in D 2 in
2°. Linearna lastnost. Če sta funkciji f(x, y) in g(x, y) integrabilni v domeni D, kaj? in? - poljubna realna števila, nato funkcija [? f(x, y) + ?g(x, y)] je tudi integrabilen v domeni D in
3°. Če sta funkciji f(x, y) in g(x, y) integrabilni v domeni D, potem je tudi produkt teh funkcij integrabilen v D.
4°. Če sta obe funkciji f(x, y) in g(x, y) integrabilni v domeni D in povsod v tej domeni f(x, y)? g(x, y), potem
5°. Če je funkcija f(x, y) integrabilna v domeni D, potem je funkcija |f(x, y)| je integrabilen v domeni D in
(Seveda integrabilnost |f(x, y)| v D ne implicira integrabilnosti f(x, y) v D.)
6°. Izrek o srednji vrednosti. Če sta obe funkciji f(x, y) in g(x, y) integrabilni v domeni D, je funkcija g(x, y) nenegativna (nepozitivna) povsod v tej domeni, M in m pa sta najboljše zgornje in spodnje meje funkcije f( x, y) v domeni D, potem obstaja število?, ki izpolnjuje neenakost m ? ? ? M in tako, da formula
Zlasti, če je funkcija f(x, y) zvezna v D in je domena D povezana, potem v tej domeni obstaja taka točka (?, ?), kaj? = f(?, ?) in formula postane
7°. Pomembna geometrijska lastnost. enako površini regije D
Naj bo v prostoru podano telo T (slika 2.1), ki je od spodaj omejeno z območjem D, od zgoraj - z grafom zvezne in nenegativne funkcije) z \u003d f (x, y,), ki je definiran v območju D, s strani - s cilindrično površino, katere vodilo je mejna domena D, generatorji pa so vzporedni z osjo Oz. Telo te vrste se imenuje cilindrično telo.
1.3 Geometrijska interpretacija dvojnega integrala





1.4 Koncept dvojnega integrala za pravokotnik
Naj bo poljubna funkcija f(x, y) definirana povsod na pravokotniku R = ? (Glejte sliko 1).

Razdelimo odsek a? x? b na n delnih segmentov z uporabo točk a = x 0< x 1 < x 2 < ... < x n = b, а сегмент c ? y ? d на p частичных сегментов при помощи точек c = y 0 < y 1 < y 2 < ... < y p = d.
Ta delitev z ravnimi črtami, vzporednimi z osema Ox in Oy, ustreza delitvi pravokotnika R na n · p delnih pravokotnikov R kl = ? (k = 1, 2, ..., n; l = 1, 2, ..., p). Navedeno razdelitev pravokotnika R bomo označili s simbolom T. V nadaljevanju, v tem razdelku, bo izraz "pravokotnik" pomenil pravokotnik s stranicami, vzporednimi s koordinatnimi osemi.
Na vsakem delnem pravokotniku R kl izberemo poljubno točko (? k , ? l). Če postavimo?x k = x k - x k-1 , ?y l = y l - y l-1 , označimo z?R kl ploščino pravokotnika R kl . Očitno je ?R kl = ?x k ?y l .
se imenuje integralna vsota funkcije f(x, y), ki ustreza danemu razdelku T pravokotnika R in dani izbiri vmesnih točk (?k, ?l) na delnih pravokotnikih razdelka T.
Diagonalo bomo imenovali premer pravokotnika R kl. Simbol? označujemo največji od premerov vseh delnih pravokotnikov R kl.
Število I imenujemo limita integralnih vsot (1) za? > 0, če za katero koli pozitivno število? ali lahko določite tako pozitivno število?, kaj če?< ? независимо от выбора точек (? k , ? l) на частичных прямоугольниках R выполняется равенство
| ? - Jaz |< ?.
Funkcija f(x, y) se imenuje integrabilna (po Riemannu) na pravokotniku R, če obstaja končna meja I integralnih vsot te funkcije pri? > 0.
Ta meja I se imenuje dvojni integral funkcije f(x, y) nad pravokotnikom R in je označena z enim od naslednjih simbolov:
Komentiraj. Na enak način kot za enkratno določen integral ugotovimo, da je vsaka funkcija f(x, y), ki jo je mogoče integrirati na pravokotniku R, omejena na ta pravokotnik.
To daje podlago, da v nadaljevanju upoštevamo le omejene funkcije f(x, y).
Problem, ki vodi do koncepta dvojnega integrala.
Predpostavimo, da je funkcija delov definirana na ![]() in zapiši vsoto
in zapiši vsoto

ki se imenuje integral.
O: Pod določenim integralom (d.i.) funkcije in izbire ![]()
Oznaka: 
Števila imenujemo integrabilna (po Riemannu) na .
T. obstoj: pod pogojem, da .
V skladu z definicijo o.i. upoštevajte, da je integral odvisen od oblike, omejitev in, vendar ni odvisen od simbola oznake spremenljivke, izražene drugače

V skladu s členoma 17.1.1 in 17.1.2 ter definicijo o.i. zapišemo formule za območje krivuljnega trapeza:  , delovna sila
, delovna sila ![]()
na: 
Pojem dvojnega integrala, integralne vsote.
Obstoj dvojnega integrala, tj. meje integralne vsote za se zdi očiten, saj ta meja podaja prostornino valjastega telesa. Vendar ta utemeljitev ni stroga. V bolj popolnih tečajih je ta trditev strogo dokazana in se imenuje izrek o obstoju dvojnega integrala.

Izrek o obstoju. Za vsako funkcijo, ki je zvezna v omejenem zaprtem območju s površino a, obstaja dvojni integral, tj. obstaja limita integralnih vsot z neomejenim naraščanjem števila majhnih območij, pod pogojem, da se vsako od njih skrči na točko . Ta meja ni odvisna od načina delitve regije na dele, niti od izbire točk
V nadaljevanju bomo obravnavali samo funkcije, ki so zvezne v domeni integracije.
Iz obstojnega izreka sledi, da lahko na primer razdelimo območje a na majhne pravokotnike z ravnimi stranicami, vzporednimi s koordinatnimi osemi (slika 230). pri čemer. Nato z izbiro točke v vsakem majhnem pravokotniku lahko zapišemo v skladu z definicijo dvojnega integrala
Da bi poudarili, da lahko dvojni integral dobimo kot limit vsote oblike, je namesto zapisa uporabljen tudi zapis
Izraz se imenuje površinski element v kartezičnih koordinatah in je enak površini pravokotnika s stranicami, vzporednimi s koordinatnimi osemi.
Upoštevajte, da pri sestavljanju integralne vsote območja, ki mejijo na mejo območja a, nimajo oblike pravokotnikov. Vendar pa je mogoče dokazati, da bo napaka pri zamenjavi takšnih območij s pravokotniki s območji v meji zmanjšana na nič.
Lastnosti dvojnih integralov
Lastnosti dvojnega integrala (in njihove izpeljave) so podobne ustreznim lastnostim enojnega določenega integrala.
1°. Aditivnost. Če funkcija f(x, l) je integrabilen v domeni D in če območje D z uporabo krivulje G območja nič je razdeljen na dve povezani regiji brez skupnih notranjih točk D 1 in D 2, nato funkcijo f(x, l) je integrabilen v vsaki od domen D 1 in D 2 in
2°. Linearna lastnost. Če funkcije f(x, l) In g(x, l) so integrabilni v domeni D, A α in β so poljubna realna števila, potem je funkcija [ α · f(x, l) + β · g(x, l)] je tudi integrabilen v domeni D, in
![]()
![]()
3°. Če funkcije f(x, l) In g(x, l) so integrabilni v domeni D, potem je tudi produkt teh funkcij integrabilen v D.
4°. Če funkcije f(x, l) In g(x, l) oba sta integrabilna v domeni D in povsod na tem območju f(x, l) ≤ g(x, l), to
5°. Če funkcija f(x, l) je integrabilen v domeni D, potem funkcija | f(x, l)| integracijski v območju D, in
(Seveda iz integrabilnosti | f(x, l)| V D integrabilnost ne sledi f(x, l) V D.)
6°. Izrek o srednji vrednosti. Če obe funkciji f(x, l) In g(x, l) so integrabilni v domeni D, funkcija g(x, l) je nenegativen (nepozitiven) povsod v tej regiji, M in m- natančne zgornje in natančne spodnje meje funkcije f(x, l) na območju D, potem je tu številka μ , ki izpolnjuje neenakost m ≤ μ ≤ M in tako, da formula
Še posebej, če funkcija f(x, l) je zvezna v D, in območje D povezan, potem je na tem območju taka točka ( ξ , η ), Kaj μ = f(ξ , η ), formula (11) pa ima obliko
Za funkcijo dveh spremenljivk, definirano kot z = f(x, l) .
Dvojni integral je zapisan takole:
Tukaj D- ploščati lik, omejen s premicami, katerih izrazi (enačbe) so podani v nalogi za izračun dvojnega integrala. Levo in desno - enakosti, v katerih je spremenljivka na levi x, in zgoraj in spodaj - z enakostmi, v katerih je spremenljivka na levi l. To mesto in naprej je eno najpomembnejših za razumevanje tehnike izračuna dvojnega integrala.
Izračunajte dvojni integral - pomeni najti število, ki je enako površini omenjene figure D .
Dokler se ne dotaknemo definicije dvojnega integrala , naučili pa se ga bomo izračunati. Lažje je razumeti, kaj je dvojni integral, ko je bilo za izračun rešenih več problemov, zato boste definicijo dvojnega integrala našli na koncu te lekcije. Če pogledamo malo naprej, lahko le ugotovimo, da je z omenjeno sliko povezana tudi definicija dvojnega integrala D .
Če je slika D je pravokotnik, vse črte, ki ga omejujejo, so ravne črte. Če je slika D- krivuljasto, nato pa je na levi in desni omejena z ravnimi črtami, od zgoraj in spodaj pa z ukrivljenimi črtami, ki jih določajo enakosti, podane v nalogi. Obstajajo tudi primeri, ko figura D- trikotnik, a o takih primerih malo dlje.
Za izračun dvojnega integrala je torej potrebno razvrstiti črte, ki mejijo na sliko D, ki ima strogo ime - regija integracije. Razvrsti na levo in desno ter zgoraj in spodaj. To bo potrebno, ko redukcija dvojnega integrala na iterirani integral – metoda izračuna dvojnega integrala.
Primer pravokotne površine:

Primer ukrivljene regije:

In to je že rešitev nam znanih določenih integralov, v katerih sta določeni zgornja in spodnja meja integracije. Izrazi, ki določajo črte, ki omejujejo obliko D, bodo meje integracije za običajne določene integrale, ki se jim že približujemo.
Redukcija dvojnega integrala na iterirani
Ohišje pravokotne površine
Naj ima taka funkcija dvojni integral
Za izračunajte ta dvojni integral , ga morate reducirati na iterirani integral, ki ima obliko
![]() .
.
Najprej morate izračunati notranji (desni) določeni integral, nato še zunanji (levi) določeni integral.
Vloge lahko zamenjate x in l
![]() .
.
Primer 1 Izračunajte dvojni integral

Izračunamo notranji (desni) integral, pri čemer upoštevamo y konstanto. Prejmemo.
 .
.

Primer 2 Izračunajte dvojni integral
![]() ,
,
rešitev. Ta dvojni integral reduciramo na iterirani integral
Na risbi gradimo območje integracije:


Zdaj izračunamo zunanji (levi) integral iz pravkar izračunanega notranjega (desnega) integrala:
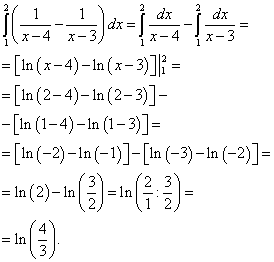
Rezultat bo rešitev tega dvojnega integrala.
Sami izračunajte dvojni integral in si nato oglejte rešitev
Primer ukrivljene ali trikotne regije
Naj bo spet dana funkcija dveh spremenljivk f(x, l) , in omejitve za D: ima nekoliko drugačen videz:
Ta zapis pomeni, da je slika D meja na levi in na desni, kot v primeru premočrtnega območja - ravne črte x = a in x = b, spodaj in zgoraj pa sta krivulji, ki ju podajata enačbi in . Z drugimi besedami, in so funkcije.
Naj ima tudi takšna funkcija dvojni integral
Za izračun tega dvojnega integrala ga moramo reducirati na iterirani integral, ki ima obliko
 .
.
Tukaj so meje integracije a in b so števila, in in sta funkciji. V primeru trikotne regije je ena od funkcij ali enačba ravne črte. Ta primer bo obravnavan v primeru 3.
Tako kot v primeru premočrtnega območja morate najprej izračunati desni določeni integral, nato še levi določeni integral.
Na enak način lahko tudi zamenjate vlogi. x in l. Potem bo imel iterirani integral obliko
 .
.
Tak iteriran integral je treba rešiti na popolnoma enak način: najprej notranji (desni) integral, nato zunanji (levi).
Primer 5 Izračunajte dvojni integral
![]() ,
,
rešitev. Ta dvojni integral reduciramo na iterirani integral
![]() .
.
Na risbi gradimo območje integracije in vidimo, da je trikotno:

Izračunamo notranji (desni) integral, pri čemer upoštevamo x kot konstanto. Prejmemo.

Zdaj izračunamo zunanji (levi) integral pravkar izračunanega notranjega (desnega) integrala. Najprej ta integral predstavimo kot vsoto integralov:
![]() .
.
Izračunamo prvi člen:

Izračunamo drugi člen:

Izračunamo tretji člen:

Dobimo vsoto, ki bo rešitev tega dvojnega integrala:
![]() .
.
Primer 6 Izračunajte dvojni integral
rešitev. Ta dvojni integral reduciramo na iterirani integral
Na risbi gradimo območje integracije:

Izračunamo notranji (desni) integral, pri čemer upoštevamo x kot konstanto. Prejmemo.
 .
.
Zdaj izračunamo zunanji (levi) integral iz pravkar izračunanega notranjega (desnega) integrala:

Rezultat bo rešitev tega dvojnega integrala.
x- prav in narobe l-pravilne in nepravilne domene integracije
Zgodi se, da je območje integracije dvojnega integrala omejeno s takšnimi črtami, da je treba območje integracije razdeliti na dele in vsak ustrezen iterirani integral rešiti posebej. To so primeri, ko:
1) območje integracije je figura, ki ima dve ali več dveh ravnih ali ukrivljenih črt v obliki spodnje ali zgornje (leve ali desne) meje;
2) območje integracije je figura, katere meja se črte sekajo v več kot dveh točkah.
Če zgoraj navedeno velja za levo ali desno mejo integracijskega območja, to so omejitve, podane s črtami, izraženimi s x, potem se imenuje domena integracije x- narobe. Če ravna črta l = l0 seka ustrezno mejo samo v eni točki, in če samo ena črta ali krivulja služi kot meja, se območje integracije imenuje x-pravilno
Podobno, če je meja določena s črtami, izraženimi v smislu l, naravnost x = x0 seka v več kot eni točki ali če več kot ena črta ali krivulja služi kot meja, potem se območje integracije imenuje l- narobe. Izvedite znake zdaj l-pravo področje, menda čisto preprosto.
Doslej smo obravnavali primere x- nepravilno in l- redna področja integracije. Zdaj razmislite o primerih, ko je pogoj pravilnosti kršen.
Primer 7 Izračunajte dvojni integral, katerega področje integracije je omejeno s premicami l = x , xy = 1 , l = 2 .

rešitev. Področje integracije je l-napačno, saj njegove spodnje obrobe ni mogoče nastaviti z eno vrstico l = l(x) . Kot lahko vidite na zgornji sliki, je spodnja meja sestavljena iz l = x(temno bordo) in xy= 1 (zeleno). Zato neposredno x= 1 (črno) lahko integracijsko območje razdelimo na dva dela - in .
Ta dvojni integral se izračuna na naslednji način:

Spreminjanje vrstnega reda integracije
Kot je navedeno zgoraj, lahko spremenljivke spremenimo po redukciji dvojnega integrala na iterirani integral x in l vloge ali, z drugimi besedami, spremeniti vrstni red integracije.
Spremembo vrstnega reda integracije lahko figurativno opišemo z naslednjimi besedami O'Henryja: "Tako se obnaša prebivalec džungle - zver, ki je prišla v kletko, in tako se obnaša prebivalec kletke. - človek, izgubljen v džungli dvomov." Rezultat je, tudi po besedah O "Henryja, en in isti: "Chalmers je pismo raztrgal na tisoč drobnih koščkov in začel mučiti svojo drago preprogo, jo premikati nazaj in naprej." ( O.Henry. Šeherezada s trga Madison Square.)
Potem, če imamo levi integral nad spremenljivko x, in pravega l, potem bo po spremembi vrstnega reda integracije vse obratno. Potem si je treba meje integracije za "novi" y "izposoditi" od "starega" x, meje integracije za "novi" x pa dobiti v obliki inverzna funkcija, razrešitev enačbe glede na x, ki določa mejo za y.
Primer 8
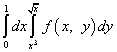 .
.
rešitev. Po spremembi vrstnega reda integracije postane integral po y levi, integral po x pa desni. Integracijske meje za »novega« igralca si bomo izposodili od »starega« X-a, torej spodnja meja je enaka nič, zgornja pa ena. Meje integracije za "starega" igralca podajajo enačbe in . Ko rešimo te enačbe glede na x, dobimo nove meje integracije za x:
(spodnji) in (zgornji).
Tako bo po spremembi vrstnega reda integracije iterirani integral zapisan takole:
 .
.
Po spremembi vrstnega reda integracije v dvojnem integralu se integracijska domena pogosto spremeni v l- napačno oz x- nepravilno (glej prejšnji odstavek). Nato je potrebno območje integracije razdeliti na dele in rešiti vsak pripadajoči iterirani integral posebej.
Ker delitev področja integracije na dele mnogim študentom predstavlja določene težave, se ne bomo omejili na primer iz prejšnjega odstavka, ampak bomo analizirali še nekaj primerov.
Primer 9 Spremenite vrstni red integracije za ponovljeni integral
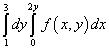 .
.
rešitev. Torej je območje integracije tega iteriranega integrala omejeno z ravnimi črtami l = 1 , l = 3 , x = 0 , x = 2l .
Pri integraciji v drugačnem vrstnem redu je spodnja meja regije sestavljena iz dveh ravnih črt: AB in pr. n. št, ki jih podajajo enačbe l= 1 in l = x/2 , kar je razvidno iz spodnje slike.

Izhod iz takšne negotovosti je razdelitev področja integracije na dva dela. Območje integracije bo razdeljeno z ravno črto BM. Nove integracijske meje se izračunajo z iskanjem inverzne funkcije. Po tej rešitvi bo iterirani integral po spremembi vrstnega reda integracije enak vsoti dveh integralov:

Seveda bo rešitev dvojnega integrala enaka, kar se reducira na iterirani integral, podan v pogoju tega primera.
Primer 10 Spremenite vrstni red integracije za ponovljeni integral
 .
.
rešitev. Torej je območje integracije iteriranega integrala omejeno z ravnimi črtami x = 0 , x= 2 in krivulje in .
Kot je razvidno iz spodnje slike, je ravna črta vzporedna z osjo 0x, bo sekal spodnjo mejo integracijske regije v več kot dveh točkah.

Zato integracijsko domeno razdelimo na tri dele z ravnimi črtami, ki so na sliki narisane črno. Nove integracijske meje se izračunajo z iskanjem inverzne funkcije. Omejitve za tri nova področja integracije bodo naslednje.


Po tej rešitvi bo ponovljeni integral po spremembi vrstnega reda integracije enak vsoti treh integralov:

Ista vsota treh integralov bo enaka dvojnemu integralu, ki se reducira na ponovljeni integral, podan v pogoju tega primera.
Pa vendar višja sila študente pogosto ovira že pri prejšnjem koraku – postavljanju meja integracije. Zaskrbljenost in zmeda nista brez podlage: če je navadno dovolj, da pogledamo risbo, da razdelimo integracijsko domeno na dele in rešimo ponavljajoči se integral – tabelo integralov, potem je pri postavljanju meja potrebnih nekaj izkušenj z usposabljanjem. integracija. Preletimo primer, v katerem se zadržimo le pri ureditvi meja povezovanja in – skoraj samodejno – pri razdelitvi regije, samo rešitev pa izpustimo.
Primer 11. Poiščite meje integracije dvojnega integrala, če je območje integracije D nastavite kot sledi:
l - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.
rešitev. izrecno (prek x in l"brez nečistoč") črte, ki omejujejo območje integracije, niso določene. Ker se za x najpogosteje izkažejo za ravne črte, ki se na eni točki dotikajo zgornje in spodnje meje, izražene z y, bomo šli točno po tej poti. Še več, ob spremembi vrstnega reda integracije dobimo območje integracije z enakim območjem. Rešimo neenakosti za igralca in dobimo:
l ≤ 2x;
l ≥ x/2;
l ≤ 2/x.
Nastale črte gradimo na risbi. Meje integracije glede na x so res premice x= 0 in x= 2. Toda regija integracije se je izkazala za l-napačno, saj njegove zgornje meje ni mogoče nastaviti z eno vrstico l = l(x) .
Morda bi bilo koristno prebrati:
- Dan svetih žena, ki nosijo miro;
- Pasijonosec Jevgenij Botkin Mučenik Jevgenij Botkin;
- Sveti rap: Čuvaški "Okhlobystin" z recitativom uči najstnike ljubezni in ponižnosti;
- Škofijski misijonski tečaji: Predavanje o misijonskem delu protodiakona A;
- Kako razumeti, kaj je všeč škorpijonu;
- Zombi apokalipsa na spletu s prijatelji;
- Igre na spletu igranje zombi apokalipse;
- Težave pri zagonu igre Fifa;