Вершини трапеції. Матеріал з геометрії на тему "трапеція та її властивості". Властивості рівнобедреної трапеції
Г.І. Ковальова
МЕТОДИКА ВИВЧЕННЯ ВЛАСТИВОСТЕЙ ТРАПЕЦІЇ
У матеріалах різних контрольних робіт та іспитів часто зустрічаються завдання на трапецію, вирішення яких вимагає від учнів знань «непрограмних» властивостей трапеції. (Програмними вважаються властивість середньої лініїтрапеції, властивості діагоналей та кутів рівнобедреної трапеції.) Якими ж чудовими властивостями володіє трапеція? Де та коли їх вивчати у шкільному курсі геометрії?
Методика вивчення властивостей трапеції
Тепер, коли ми бачили кілька типів, давайте дізнаємося про фігури, які не мають властивостей паралелограмів. Нагадаємо, що паралелограми є чотирикутниками, протилежні сторони яких паралельні. У цьому розділі ми розглянемо чотирикутники, протилежні сторони яких можуть перетинатися деякою точкою. Почнемо наше дослідження, вивчивши деякі властивості трапецій. Визначення. Трапеція є чотирикутником з рівно однією парою паралельних сторін.
Після вивчення властивості середньої лінії трапеції можна сформулювати та довести властивість відрізка, що з'єднує середини діагоналей трапеції. Відрізок, що з'єднує середини діагоналей трапеції, дорівнює напіврізниці основ.
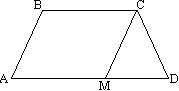
Відпрацьовуючи основний прийом розв'язання задач на трапецію «провести дві висоти», учням необхідно запропонувати завдання: «Нехай BT- Висота рівнобедреної трапеції ABCDз основами BCі AD.
 ,
,
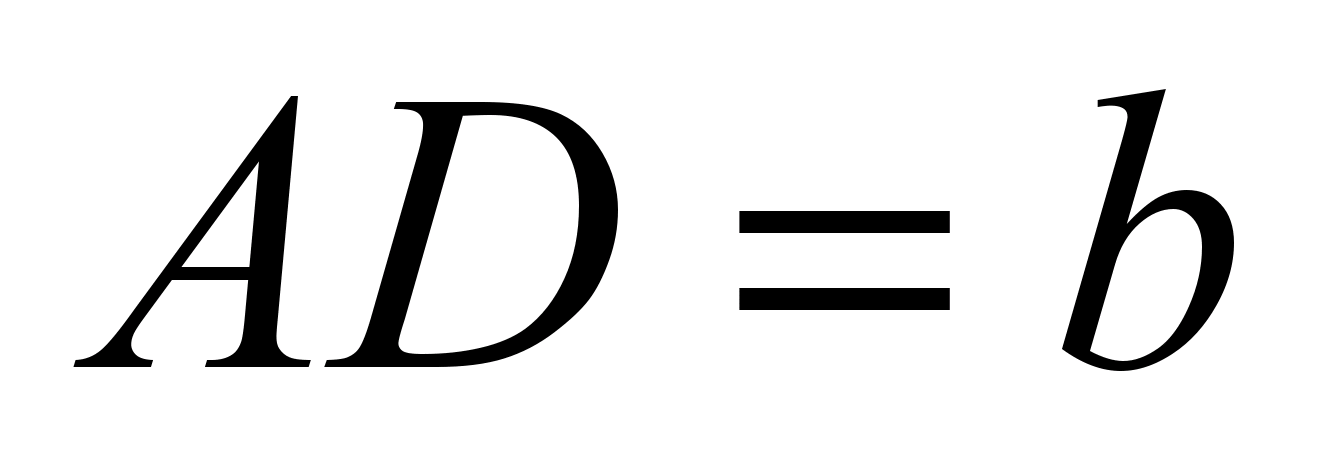 . Знайдіть довжини відрізків ATі TD».
. Знайдіть довжини відрізків ATі TD».
«Використання тригонометрії під час вирішення планиметричних завдань»
Оскільки трапеція повинна мати рівно одну пару паралельних сторін, нам потрібно буде довести, що одна пара протилежних сторін є паралельною, а інша - не в нашій. Якщо ми забудемо довести, що одна пара протилежних сторін не є паралельною, ми не виключаємо можливість того, що чотирикутник є паралелограмом. Тому цей крок буде абсолютно необхідним, коли ми будемо працювати над різними вправами, що включають трапеції.
Перш ніж ми поринемо прямо в наше дослідження трапецоїдів, необхідно буде дізнатися імена різних частин цих чотирикутників, щоб бути конкретними щодо його сторін та кутів. Усі трапеції містять дві основні частини: основи та ноги. Протилежні сторони трапеції, паралельні одна одній, називаються основами. Інші сторони трапеції, які перетинаються у якійсь точці, якщо вони розширені, називаються ногами трапеції.
Тема «Подібність фігур» дуже благодатна вивчення властивостей трапеції. Наприклад, діагоналі трапеції розбивають її на чотири трикутники, причому трикутники, що належать до основ, подібні, а трикутники, що належать до бокових сторін, рівновеликі. Назвемо це твердження зВластивістю трикутників, на які розбивається трапеція її діагоналями. Причому перша частина твердження доводиться дуже легко через ознаку подібності трикутників по двох кутах. Другу частину можна запропонувати учням як завдання.
Подібність утворених трикутників трапеції
Верхня і нижня сторони трапеції проходять паралельно одна одній, тому є підставами трапеції. Інші сторони трапеції перетинаються, якщо вони розширені, тому є ногами трапеції. Сегмент, який сполучає середини ніг трапеції, називається середнім. Довжина цього сегмента завжди дорівнює половині суми трапецієподібних основ або.
Відношення довжин відрізків та основ
Вимірювання середнього сегмента залежить тільки від довжини трапецієподібних основ. Однак існує важлива характеристика, Що деякі трапеції мають виключно залежність від її ніг. Давайте подивимося на ці трапеції зараз. Рівностегнова трапеція – трапеція, ноги якої конгруентні. За визначенням, якщо чотирикутник має одну пару паралельних ліній, то чотирикутник є трапецією. Визначення рівнобедреної трапеції додає іншу специфікацію: ноги трапеції мають бути конгруентними.
Аналогічно трикутники
BOCі АОВмають загальну висоту, якщо прийняти за їх підстави відрізки COі OA.
Тоді 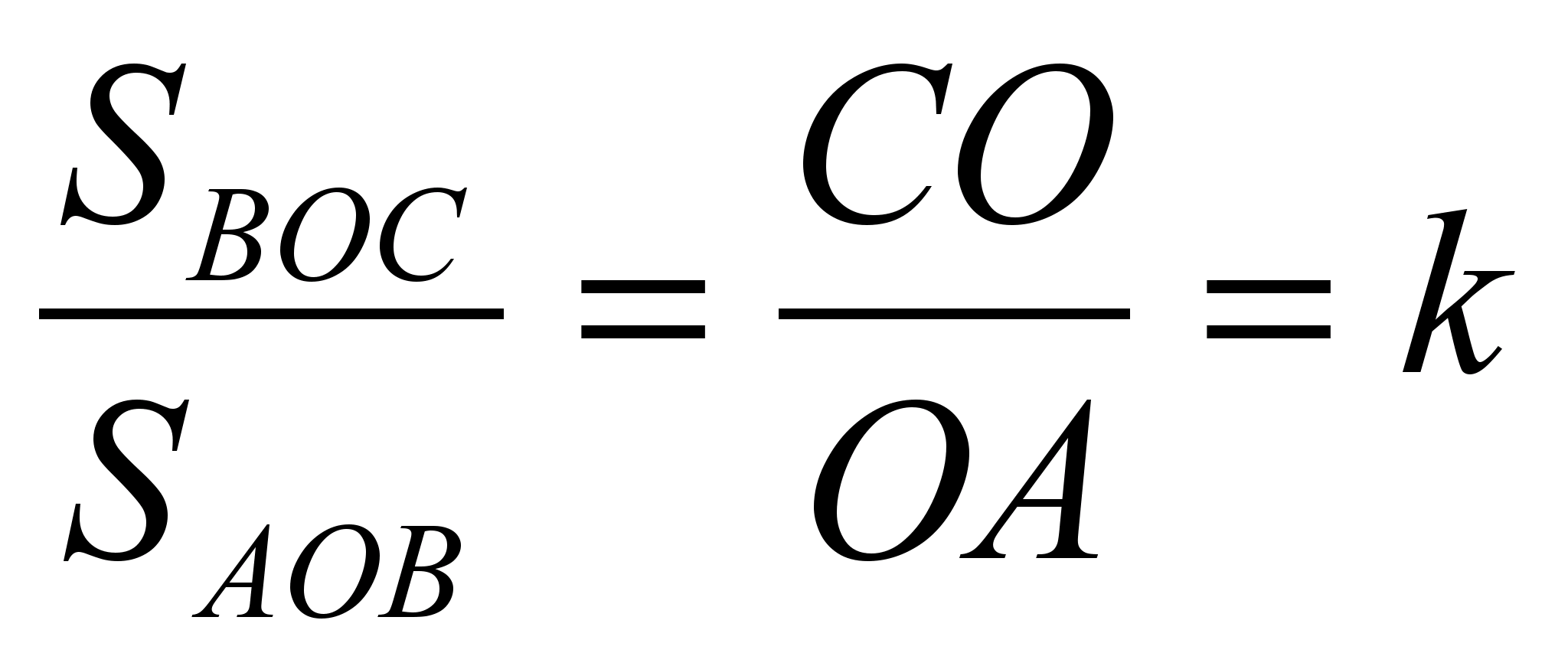 і
і 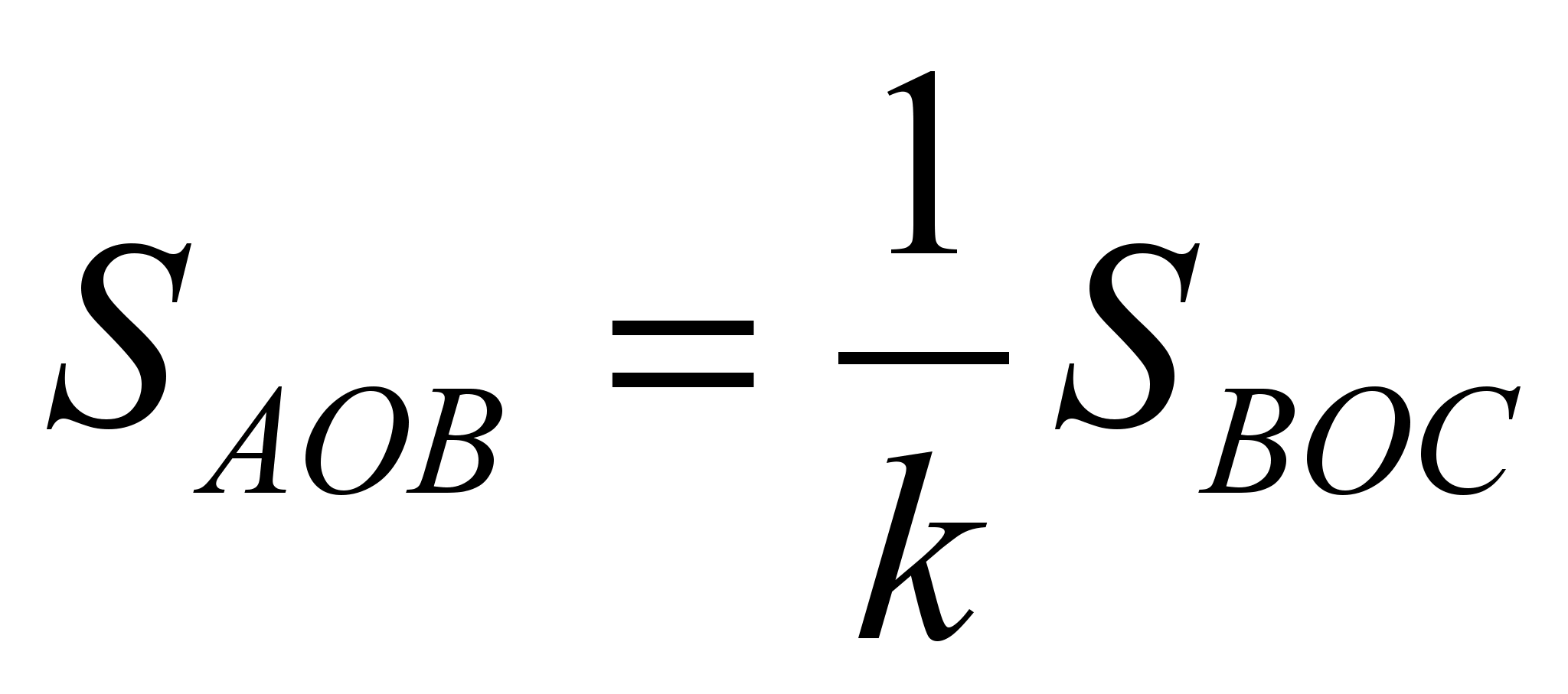 .
.
З цих двох пропозицій випливає, що 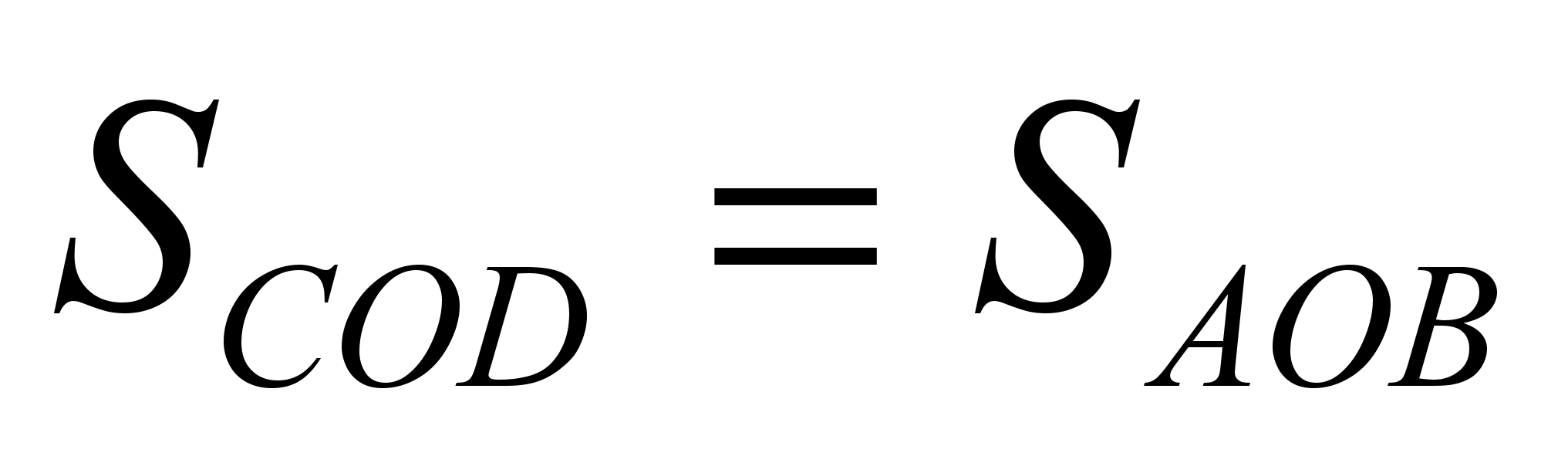 .
.
Є кілька теорем, які ми можемо використовувати, щоб допомогти нам довести, що трапеція є рівнобедреною. Ці властивості перелічені нижче. Трапеція рівнобедрена тоді і лише тоді, коли базові кути конгруентні. Трапеція є рівнобедреною, якщо і тільки якщо діагоналі конгруентні.
Якщо трапеція є рівнобедреною, її протилежні кути є додатковими. Кайт є чотирикутником з двома різними парами суміжних сторін, які є конгруентними. Нагадаємо, що паралелограми також мали пари конгруентних сторін. Проте їхні конгруентні сторони завжди були протилежними. Змії мають дві пари конгруентних сторін, які зустрічаються в двох різних точках. Давайте подивимося на наведену нижче ілюстрацію, щоб допомогти нам зрозуміти, як виглядає змій.
Було б чудово не зупинятися на сформульованому твердженні, а знайти зв'язок між площами трикутників, на які розбивається трапеція її діагоналями
, запропонувавши учням вирішити завдання: «Нехай O – точка перетину діагоналей трапеції ABCDз основами BCі AD. Відомо, що площі трикутників BOCі AODрівні відповідно  і
і 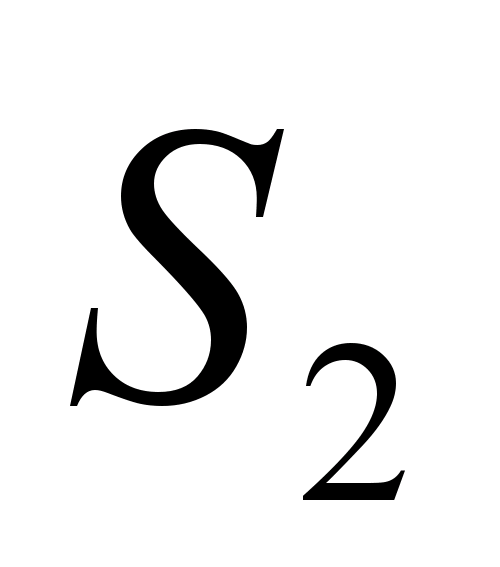 . Знайдіть площу трапеції».
. Знайдіть площу трапеції».
Кайти мають кілька властивостей, які допоможуть нам ідентифікувати їх з інших чотиристоронніх. Діагоналі кайту зустрічаються під прямим кутом. У кайтів є рівно одна пара протилежних кутів, які є конгруентними. Ці дві властивості проілюстровані на діаграмі нижче.
Це наша єдина пара конгруентних кутів, тому що? Дозвольте практиці робити деякі проблеми, які вимагають використання властивостей трапецій та повітряних зміїв, про які ми щойно дізналися. Оскільки нам дано довжини основ трапеції, ми можемо з'ясувати, якою має бути довжина середнього сегмента. Давайте використовуємо формулу, яку ми дали для середнього сегмента, щоб зрозуміти це.
Так як . Звідси, з подоби трикутників BПроCі AODвипливає, що 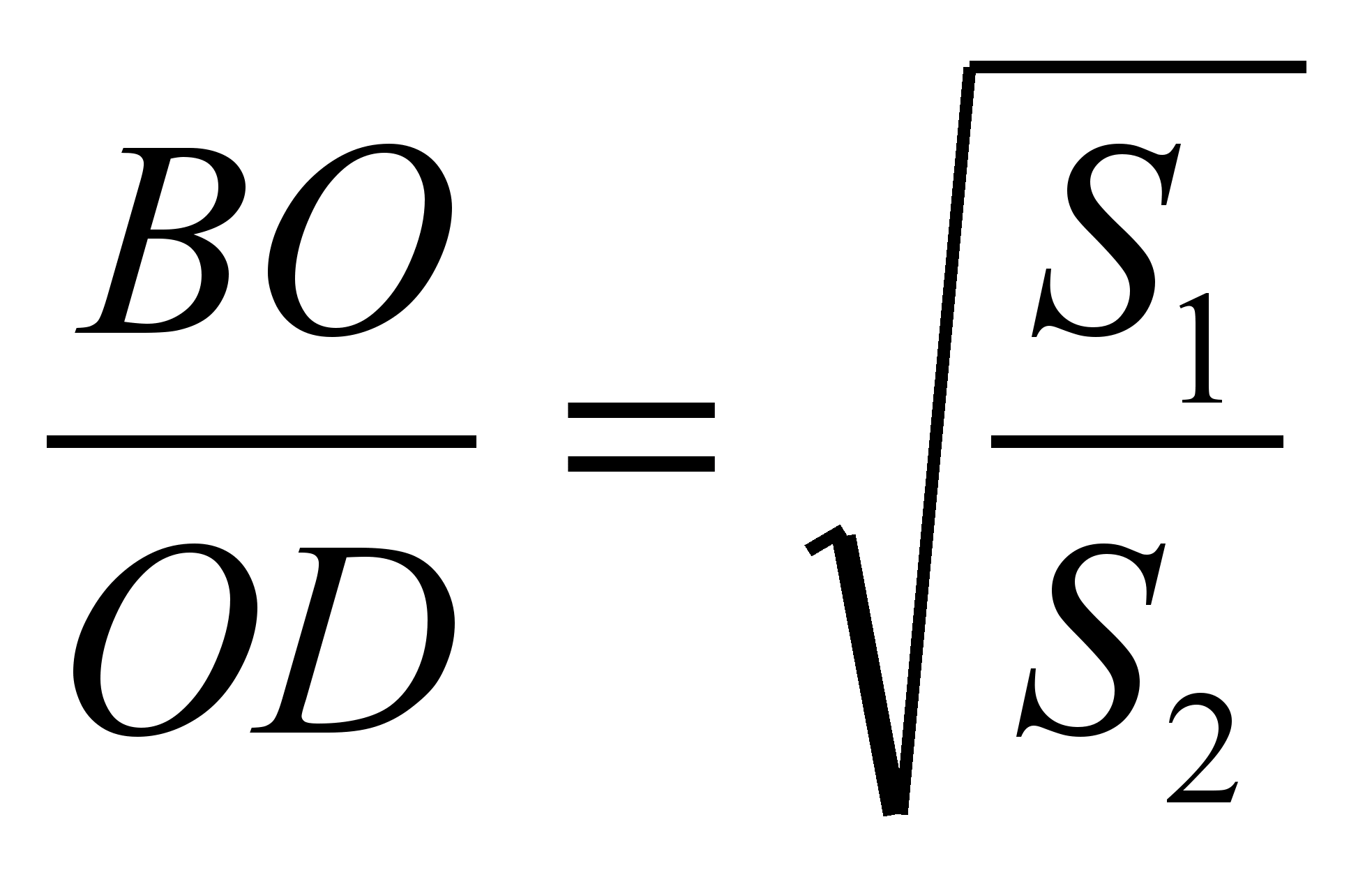 .Отже,
.Отже, 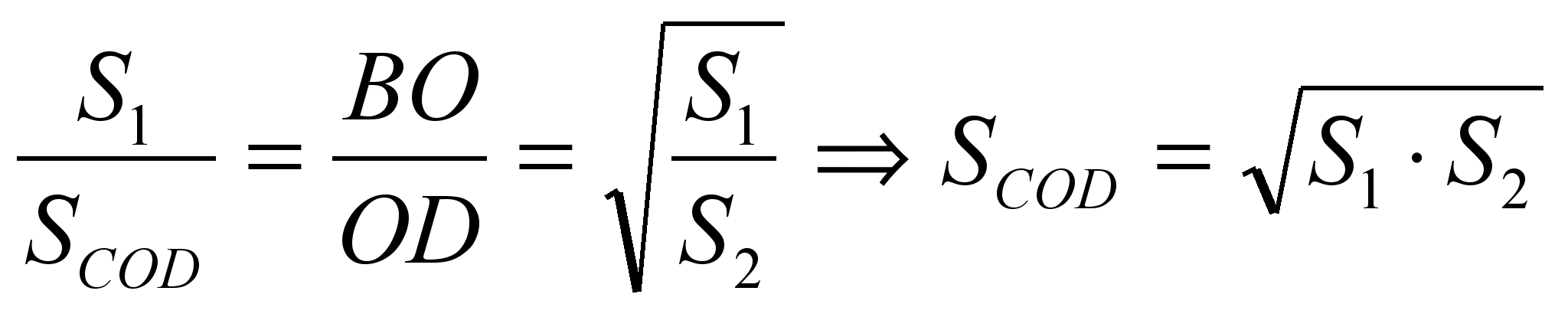 . Тоді
. Тоді
З використанням подібності доводиться і властивість відрізка, що проходить через точку перетину діагоналей трапеції паралельно до основ. Пропонуємо учням вирішити завдання: «Нехай O – точка перетину діагоналей трапеції ABCDз основами BCі AD. , . Знайдіть довжину відрізка PK, що проходить через точку перетину діагоналей трапеції паралельно до основ. На які відрізки ділиться PKточкою Про».
На малюнку нам було дано лише міра одного кута, тому ми повинні мати можливість виводити більше інформації на основі цього одного елемента. Оскільки чотирикутник є рівнобедреною трапецією, ми знаємо, що базові кути є конгруентними. Тепер давайте з'ясуємо, яка сума?
Разом вони мають загалом 128°. Нагадаємо теорему про внутрішні кути багатокутника, що внутрішні кути чотирикутника мають бути 360°. Отже, давайте спробуємо використати це таким чином, щоб допомогти нам визначити міру? Спочатку давайте підсумуємо всі кути і встановіть його рівним 360°.
Звідси 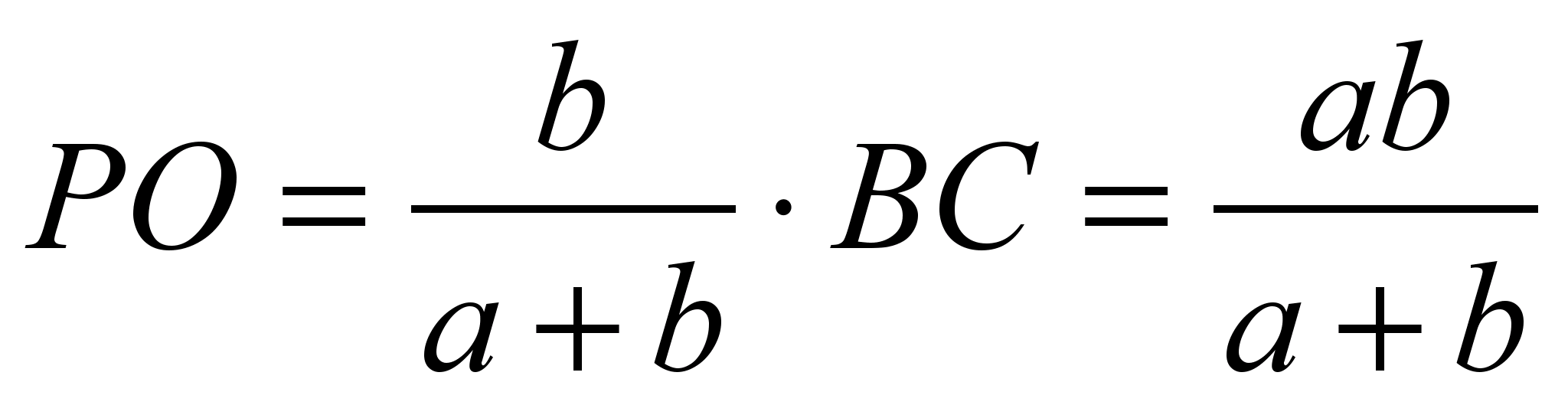 .
.
Аналогічно з подоби трикутників DOKі DBC, випливає, що 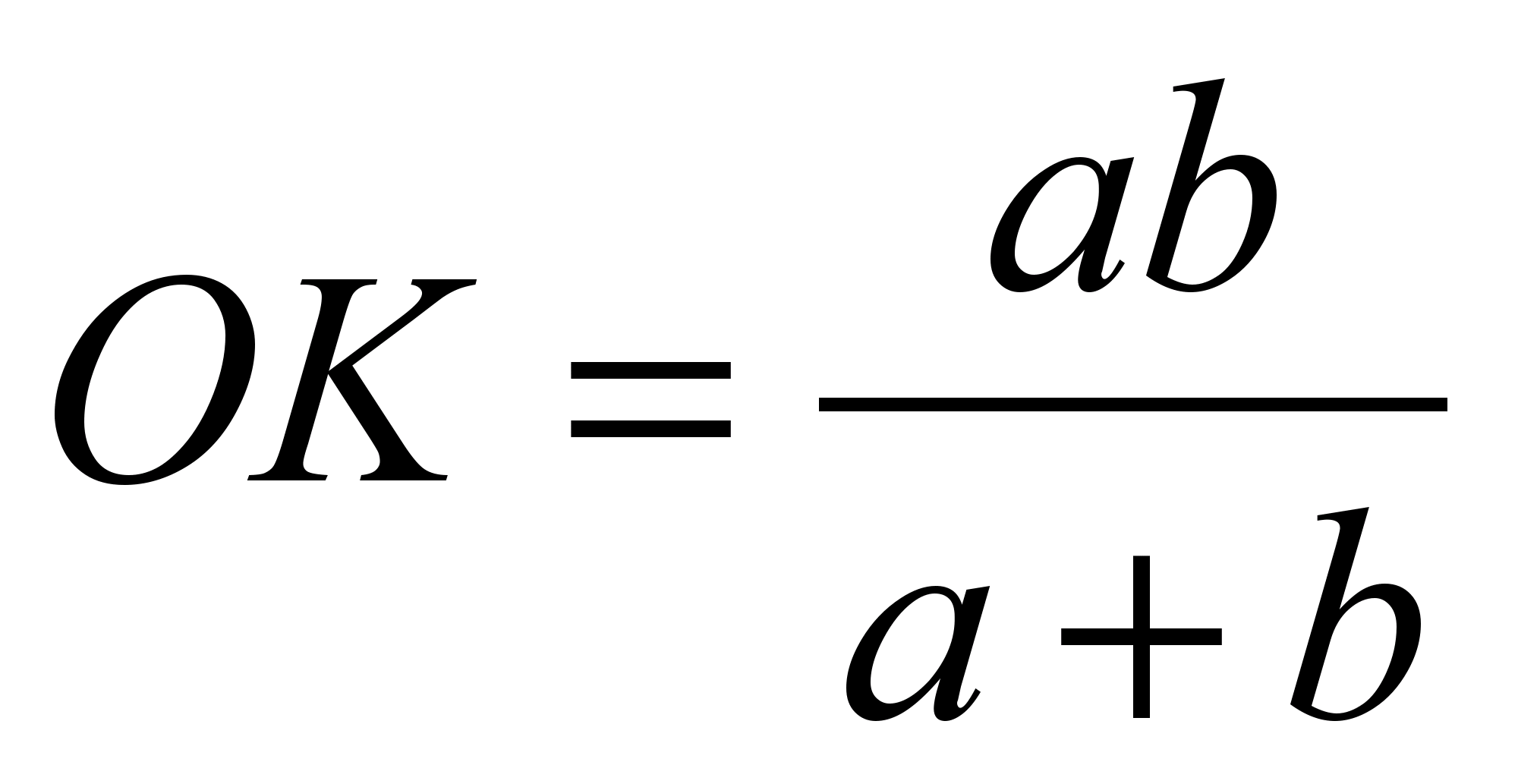 . Звідси
. Звідси 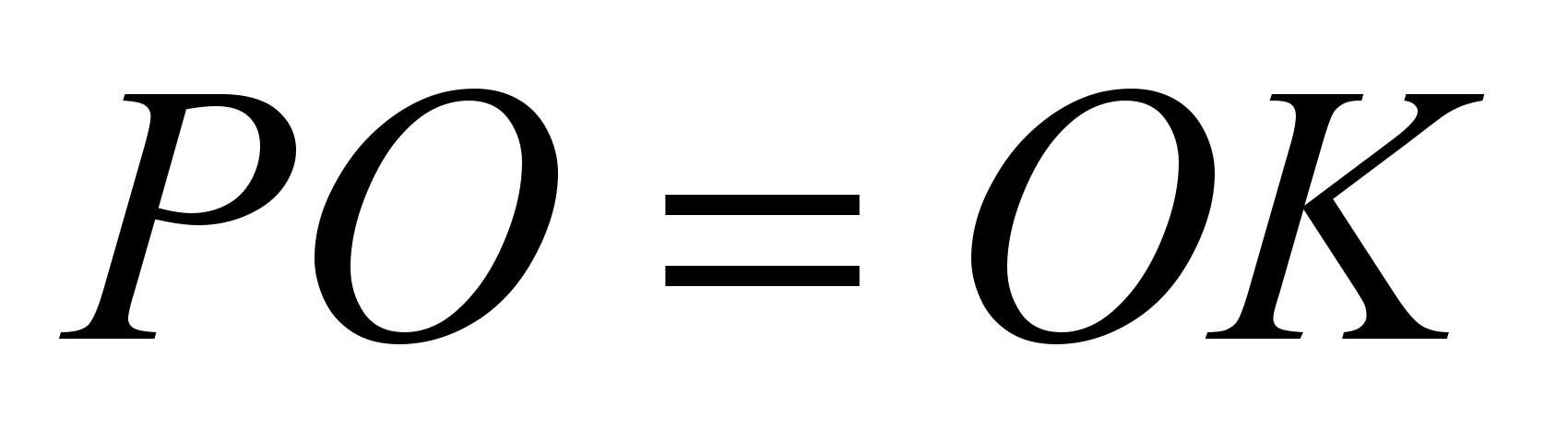 і
і 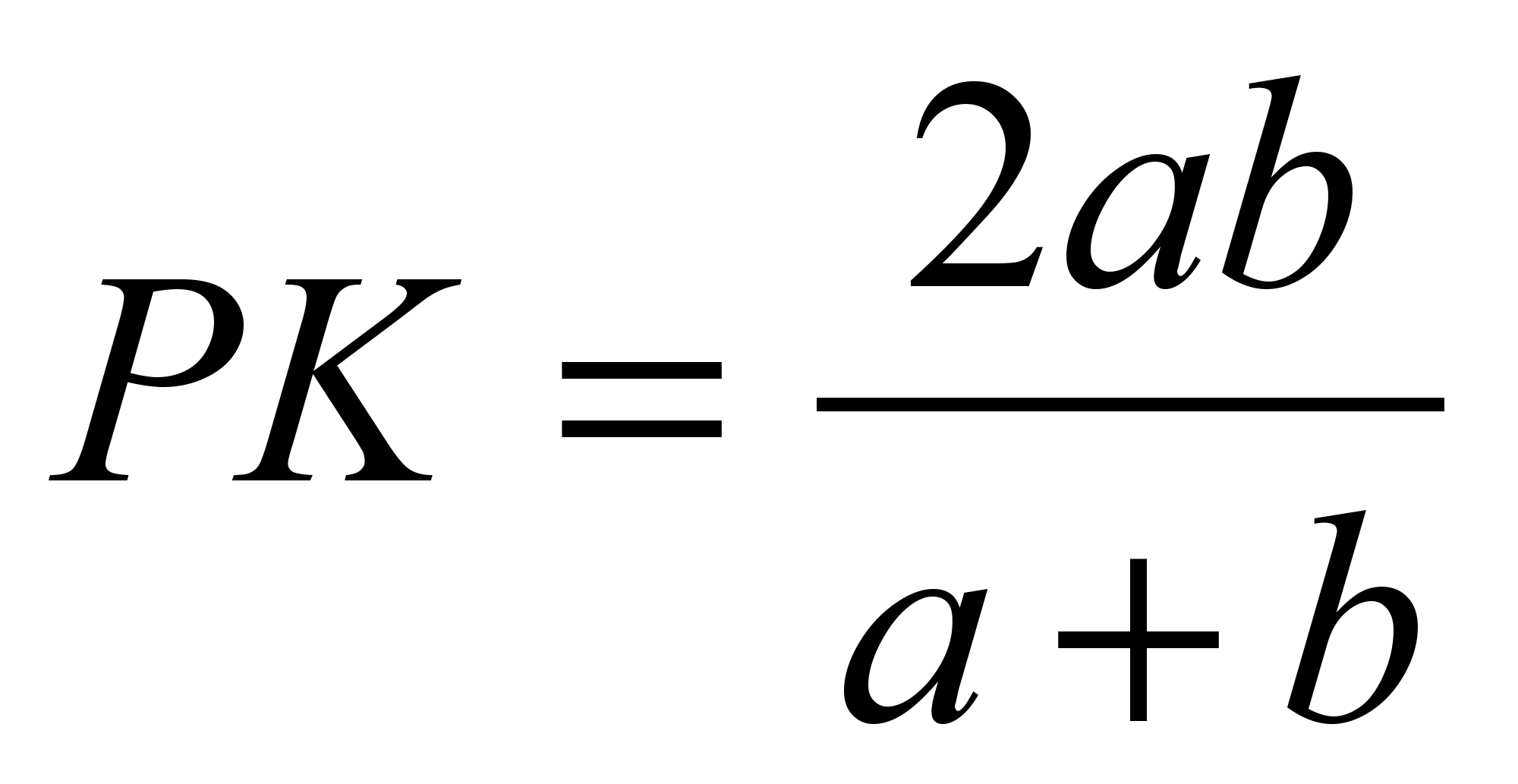 .
.
Описана біля трапеції коло
Отже, якщо ми визначаємо заходи? Це значення означає, що міра? Нарешті, ми можемо встановити 116, що дорівнює виразу, показаному в? Хоча вищеописаний метод був глибоким способом вирішення вправи, ми могли б просто використовувати властивість, що додаткові кути рівнобедрених трапецій є додатковими. Рішення таким чином відбувається набагато швидше, тому що нам потрібно лише знайти, що таке доповнення з кутом 64°.
Як тільки ми дійдемо до цієї точки в нашій проблемі, ми просто встановимо 116 рівним 4 і вирішимо, як і раніше. Чи нам також було дано це? У минулому ми вивчили кілька теорем конгруенції трикутника, які можуть бути застосовні в цій ситуації, якщо ми можемо просто знайти іншу сторону або кут, які є конгруентними.
Домагаємося від учнів усвідомлення доведеної властивості: відрізок, паралельний основам трапеції, що проходить через точку перетину діагоналей і з'єднує дві точки на бокових сторонах, ділиться точкою перетину діагоналей навпіл. Його довжина є середня гармонійна підстави трапеції.
Наступне з властивість чотирьох точок:у трапеції точка перетину діагоналей, точка перетину продовження бічних сторін, середини основ трапеції лежать на одній лінії.
Наша нова ілюстрація показано нижче. Нижче наведено двостоєчний геометричний доказ цієї вправи. Щоб отримати доступ до таких геометрій, як. Перестаньте боротися та починайте навчатися сьогодні з тисяч безкоштовних ресурсів! Властивості наведені посиланнями на відповідні уроки. Уроки перераховані у логічному порядку, а це означає, що кожен урок відноситься до попередніх. і не посилається на це. Список об'єднує відповідні уроки, які розташовані на різних сторінкахцього сайту.
Діагоналі та висота трапеції
Трапеція є рівнобедреною, якщо і тільки якщо її базові кути конгруентні. Трапеція є рівнобедреною, якщо і тільки якщо її дві діагоналі конгруентні. Середня лінія трапеції паралельна до її основ. Довжина середньої лінії трапеції становить половину суми довжин її основ. У трапеції ділянка лінії, відтягнута від середини бічної сторони, паралельна основам, перетинає іншу бічну сторону в її середній точці.
Знайомлячи учнів з подобою фігур (не трикутників), можна запропонувати знайти довжину відрізка трапеції, що розбиває, на дві подібних.
Таким чином, відрізок що розбиває трапецію на дві подібні трапеції, має довжину рівну середньому геометричному довжин основ.
Після виведення формули площі трапеції корисно довести властивість відрізка, що ділить трапецію на дві рівновеликі.
Середня лінія трапеції – це локус точок, рівновіддалених від двох прямих, що містять основи трапеції. У трапеції сума внутрішніх кутів на кінцях збоку дорівнює 180°. У трапеції середня лінія ділить навпіл будь-який відрізок прямий, що з'єднує точку більш короткому підставі з точкою більшому підставі. У трапеції відстань між серединами його діагоналей становить половину різниці довжин більших і коротших підстав.
Якщо у трапеції сума двох протилежних внутрішніх кутів дорівнює 180°, то трапеція є рівнобедреною. У рівнобедреній трапеції пряма, що проходить через діагональне перетин, паралельне основам, ділить навпіл кут між діагоналями. У рівнобедреній трапеції бічний бік видно під одним кутом від будь-якої з двох протилежних вершин.
Складемо систему 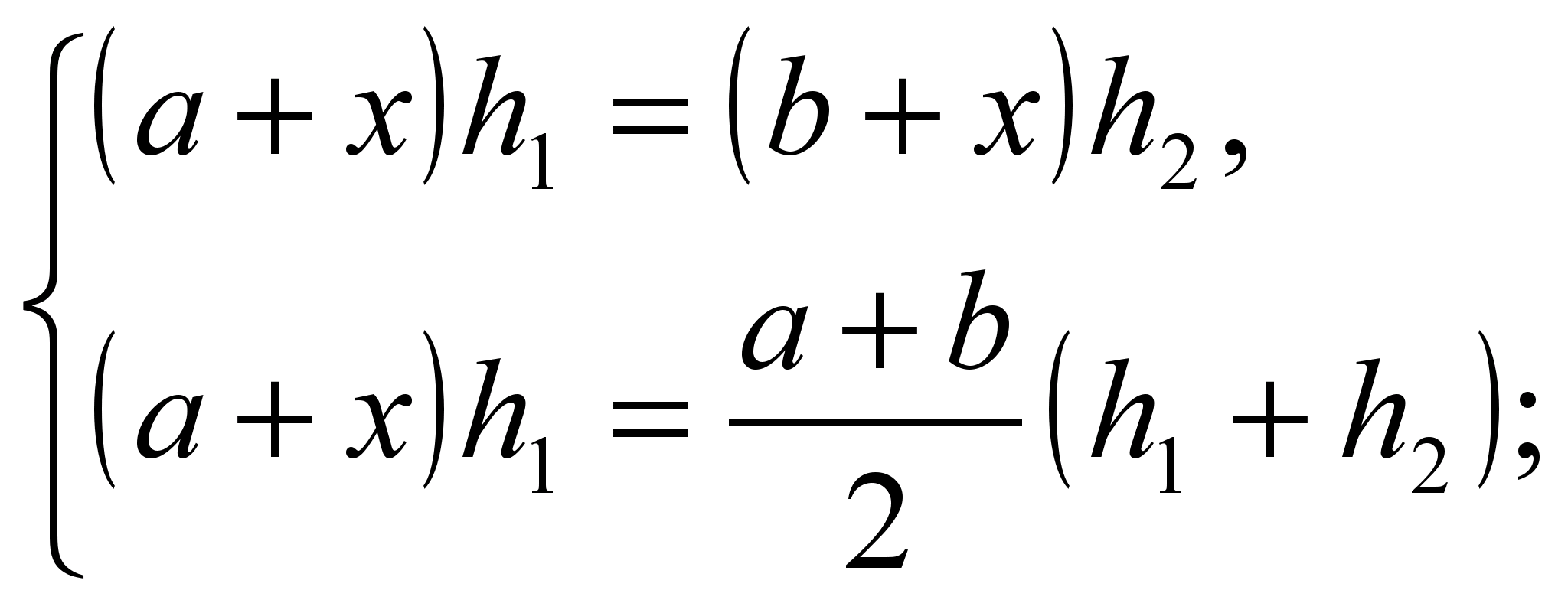
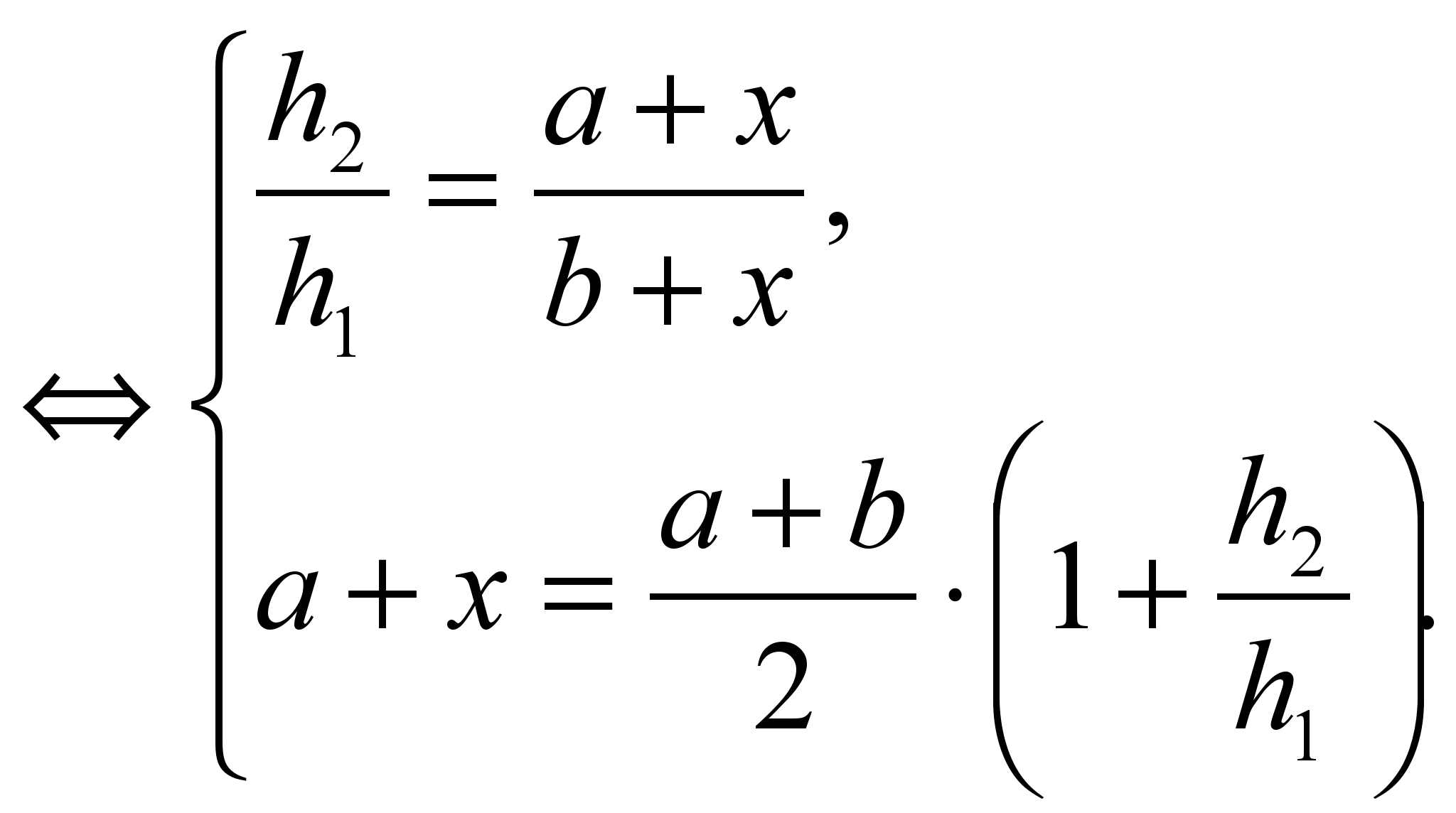
Рішення системи 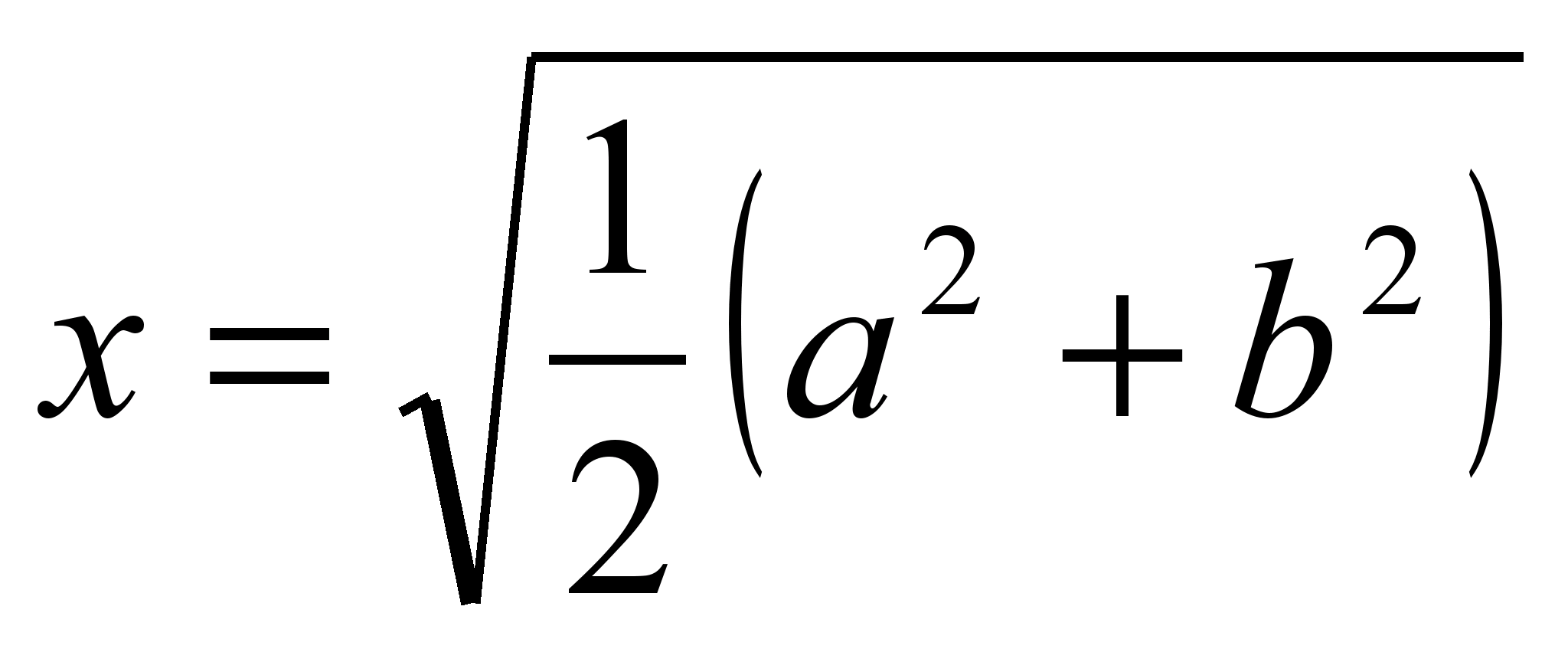 .
.
Таким чином, довжина відрізка, що ділить трапецію на дві рівновеликі, дорівнює 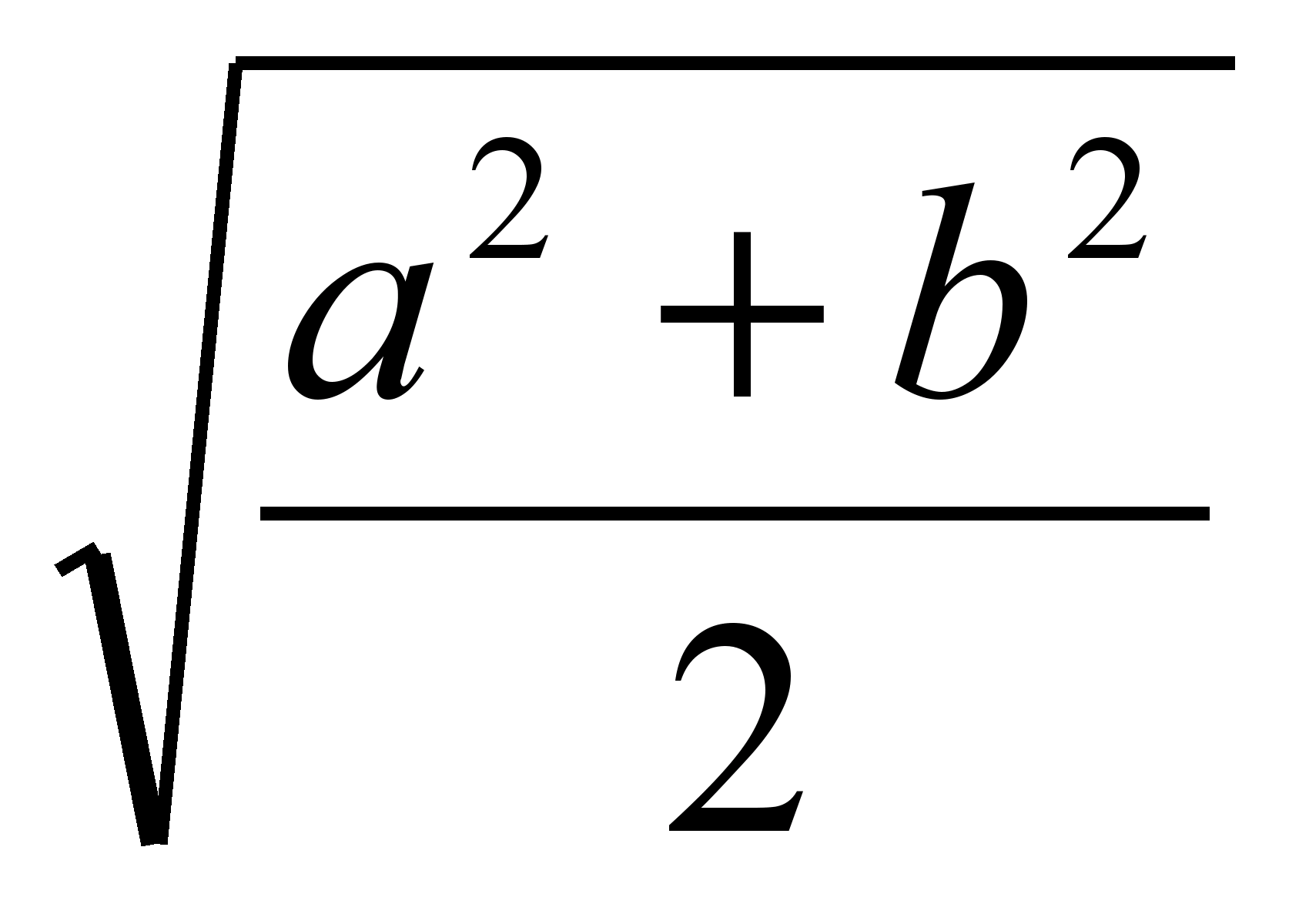 (Середньому квадратичному довжин основ).
).
(Середньому квадратичному довжин основ).
).
Тепер наводиться той же список уроків, що й короткі інструкції. У рівнобедреній трапеції базові кути конгруентні. Теорема 2. Якщо в трапеції базові кути є конгруентними, то трапеція є рівнобедреною. Вирішені проблеми У рівнобедреній трапеції базовий кут становить 73°. Знайдіть усі інші кути трапеції. У рівнобедреній трапеції базовий кут втричі менший від внутрішнього кута наприкінці більш короткої основи. Знайдіть усі кути трапеції.
У трапеції відрізок лінії, відтягнутий від середини бокової сторони, паралельної основам, перетинає іншу бічну сторону в її середині. Знайдіть довжину трапеції у середній лінії. У трапеції велика база має довжину 27 см, а вона на 10 см довша за основу.
Щоб учні усвідомили зв'язок між зазначеними відрізками, необхідно попросити збудувати їх для даної трапеції. Без зусиль учні побудують середню лінію трапеції та відрізок, що проходить через точку перетину діагоналей трапеції паралельно до основ. Де лежатиме третій і четвертий відрізок? Відповідь це питання має привести учнів до відкриття зв'язок між середніми величинами.
Знайдіть довжини трапецієподібних основ. У рівнобедреній трапеції дві діагоналі є конгруентними. Завдання 2. Якщо трапеції дві діагоналі конгруентны, то трапеція равнобедренна. Завдання 3. Будь-яка точка на середній лінії трапеції рівновіддалена від двох паралельних ліній, що містять основи трапеції. Якщо точка в площині еквідистантна від двох паралельних ліній, що містять основи трапеції, то точка належить прямої, що містить. трапеція у середній лінії. Вирішена проблема. У трапеції будь-який сегмент прямої лінії, що з'єднує точку на більш короткій основі з точкою на більшій основі, ділять навпіл на середній лінії трапеції.
Ознака та властивість вписаного та описаного чотирикутника повинні бути конкретизовані для всіх відомих учнів чотирикутників, у тому числі й для трапеції.
Властивості описаної трапеції.Біля кола можна описати трапецію тоді і лише тоді, коли сума довжин основ дорівнює сумі довжин бічних сторін.
Перше очевидно. Для доказу другого слідства необхідно встановити, що кут CODпрямий, що так само не становить великої праці. Зате знання цього слідства дозволяє під час вирішення завдань використовувати прямокутний трикутник.
У трапеції бісектриси внутрішніх кутів на кінцях збоку перетинаються під прямим кутом. У трапеції бісектриси внутрішніх кутів на кінцях збоку перетинаються в точці, що лежить на середній лінії трапеції. Завдання 4. У рівнобедреній трапеції базовий кут дорівнює 60°. Доведіть, що більш коротка базова довжина дорівнює різниці більшої довжини основи та довжини бічної сторони.
У рівнобедреній трапеції діагональ становить 10 см і становить 60° із основою. Знайдіть довжину трапеції середньої довжини. Підстави трапеції мають довжину 3 і 5 одиниць, одна діагональ перпендикулярна бічній стороні, а інша діагональ ділить навпіл кут. на більшій основі. Знайдіть висоту трапеції. Використовуючи лінійку і компас, побудуємо трапецію, яка має підстави, що збігаються з двома заданими сегментами, і бічні сторони, конгруентні. два інших заданих сегменти.
Конкретизуємо слідства для рівнобедреної описаної трапеції :
|
|
висота рівнобедреної описаної рівнобедреної трапеції є середня геометрична основ трапеції. Діагоналі та кути трапеціїВикористовуючи лінійку та компас, побудуємо трапецію, яка має підстави, що збігаються з двома заданими сегментами, а бічні сторони - конгруентні. до двох інших заданих сегментів. Геометрія - це особливий предмет математики, що стосується форм та об'єктів та пов'язаних з ними проблем. Існують різні типи геометричних фігур. Декілька важливих двовимірних фігур - це квадрат, прямокутник, трикутник, багатокутник, коло, паралелограм, трапеція, ромб і т.д. форма, обмежена чотирма сторонами, називається чотиристороннім. |
Розглянемо основні засади методики вивчення властивостей трапеції.
По-перше, це використання задачного підходу . Немає потреби вводити в теоретичний курс геометрії нові властивості трапеції. Ці властивості відкриваються і формулюються учнями через розв'язання задач (краще систем задач). Важливо, щоб учитель знав, які завдання мають бути поставлені і в якийсь момент навчального процесу. Крім того, кожна властивість може бути ключовим завданням у системі задач.
По-друге, "спіральна" організація вивчення властивостей трапеції
. До окремих властивостей можна повертатися кілька разів, тоді є можливість, що учні їх запам'ятають. Наприклад, властивість чотирьох точок можна довести щодо подібності і потім з допомогою векторів. Рівновеликість трикутників, що прилягають до боків трапеції, можна довести, використовуючи як властивість трикутників, що мають рівні висоти, проведені до сторін, що лежать на одній прямій, так і формулу 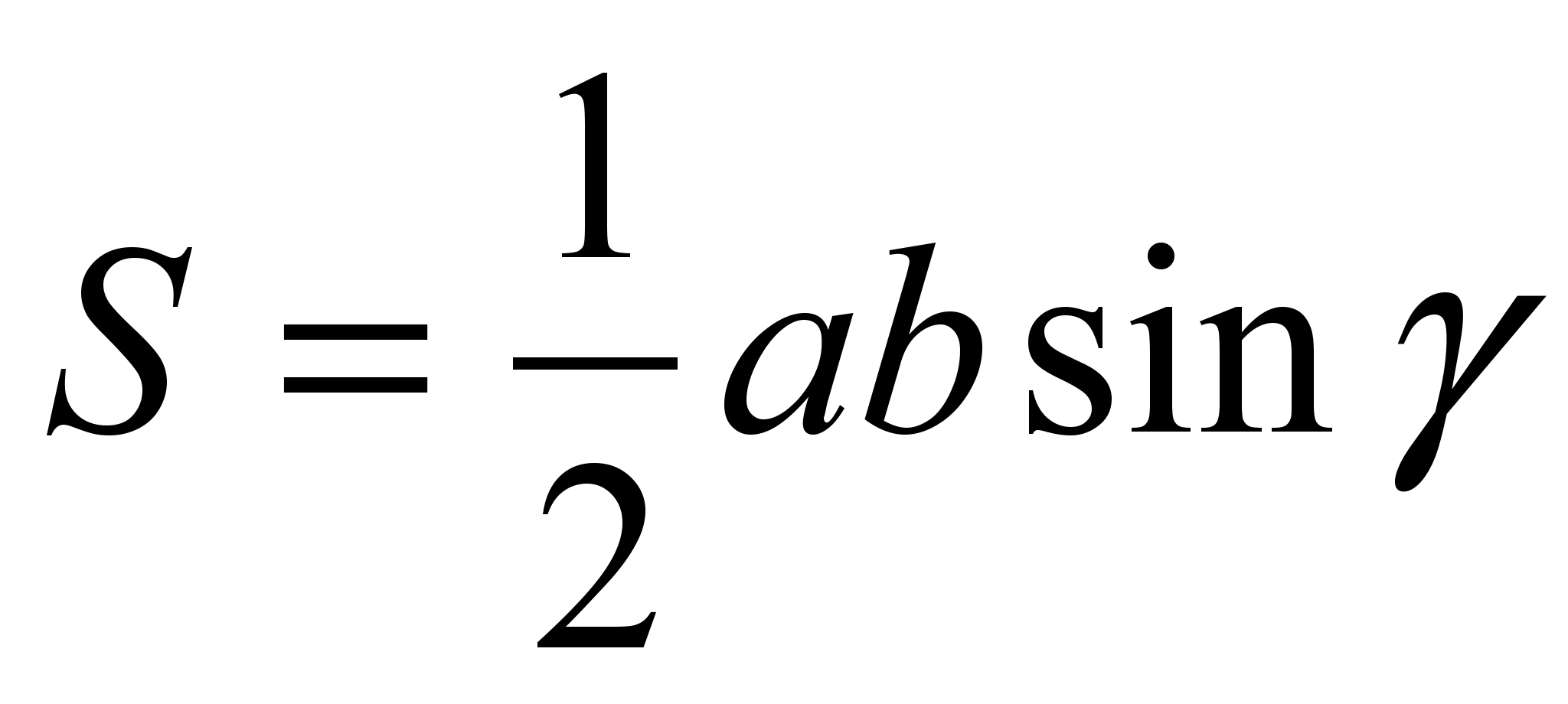 . Можна відпрацьовувати властивості прямокутного трикутника на описаній трапеції, теорему синусів на трапеції вписаної і так далі.
. Можна відпрацьовувати властивості прямокутного трикутника на описаній трапеції, теорему синусів на трапеції вписаної і так далі.
Запропоноване включення «непрограмних» властивостей трапеції до змісту шкільного курсу геометрії, задачна технологія їх вивчення, неодноразове звернення до властивостей трапеції щодо інших тем дозволять учням глибше пізнати трапецію і забезпечать успішність вирішення завдань застосування її властивостей.
Тому одну з них ми назвемо великим
, другу - малою основою
трапеції. Висотою
трапеції можна назвати будь-який відрізок перпендикуляра, проведеного з вершин відповідно протилежну сторону (для кожної вершини є дві протилежні сторони), укладений між взятими вершиною і протилежною стороною. Але можна виділити особливий виглядвисот.
Визначення 8.
Висотою основи трапеції називають відрізок прямої, перпендикулярної основ, укладений між основами.
Теорема 7
. Середня лінія трапеції паралельна основам і дорівнює їх напівсумі.
Доведення. Нехай дана трапеція АВСD та середня лінія КМ. Через точки В та М проведемо пряму. Продовжимо сторону AD через точку D до перетину з ВМ. Трикутники ВСм і МРD рівні по стороні і двом кутам (СМ=МD, ∠ВСМ=∠МDР - навхрест, ∠ВМС=∠DМР - вертикальні), тому ВМ=МР або точка М - середина ВР. КМ є середньою лінією у трикутнику АВР. За якістю середньої лінії трикутника КМ паралельна АР і зокрема АD і дорівнює половині АР: 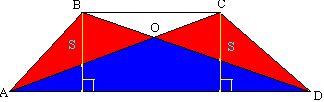 Теорема 8
. Діагоналі ділять трапецію на чотири частини, дві з яких, прилеглі до бокових боків, байдужі.
Теорема 8
. Діагоналі ділять трапецію на чотири частини, дві з яких, прилеглі до бокових боків, байдужі.
Нагадаю, що фігури називаються рівновеликими, якщо вони мають однакову площу. Трикутники АВD і АСD рівновеликі: вони мають рівні висоти (позначені жовтим) і загальне основание. Ці трикутники мають загальну частину ADD. Їх площу можна розкласти так: 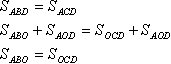
 Види трапецій:
Види трапецій:
Визначення 9.
(рис 1) Гострокутною трапецією називається трапеція, у якої кути, прилеглі до більшої основи гострі.
Визначення 10.
(рис 2) Тупокутною трапецією називається трапеція, у якої один із кутів, прилеглих до більшої основи тупий.
Визначення 11.
(рис 4) Прямокутною називається трапеція, у якої одна бічна сторона перпендикулярна до основ.
Визначення 12.
(рис 3) Рівностегнової (рівнобічної, рівнобічної) називається трапеція, у якої бічні сторони рівні.
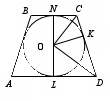
 Властивості рівнобічної трапеції:
Властивості рівнобічної трапеції:
Теорема 10
. Кути, що належать до кожної з основ рівнобічної трапеції, рівні.
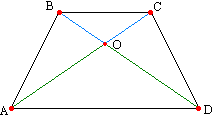
Доведення. Доведемо, наприклад, рівність кутів А і D за більшої підстави AD рівнобічної трапеції АВСD. Для цієї мети проведемо через точку С пряму паралельну бічній стороні АВ. Вона перетне велику основу у точці М. Чотирикутник АВСМ є паралелограмом, т.к. за побудовою має дві пари паралельних сторін. Отже, відрізок СМ січної прямої, укладений усередині трапеції дорівнює її бічній стороні: СМ = АВ. Звідси ясно, що СМ=СD, трикутник СМD - рівнобедрений, ∠ СМD=∠ СDM, і, отже, ∠ А=∠ D. Кути, що належать до меншої основи, також рівні, т.к. є для знайдених внутрішніми одностороннім і мають у сумі два прямі.  Теорема 11
. Діагоналі рівнобічної трапеції рівні.
Теорема 11
. Діагоналі рівнобічної трапеції рівні.
Доведення. Розглянемо трикутники АВD та ACD. Вона рівні з двох сторін і куту між ними (АВ=СD, AD - загальна, кути А і D дорівнюють теоремі 10). Тому АС = BD.
 Теорема 13
. Діагоналі рівнобедреної трапеції точкою перетину діляться відповідно рівні відрізки. Розглянемо трикутники АВD та ACD. Вона рівні з двох сторін і куту між ними (АВ=СD, AD - загальна, кути А і D дорівнюють теоремі 10). Тому ∠ ОАD = ∠ ОDA, звідси рівні і кути ОВС і ОСВ як відповідно нахресні для кутів ODA і ОАD. Згадаймо теорему: якщо у трикутнику два кути рівні, то він рівнобедрений, тому трикутники ОВС і ОAD є рівностегновими, отже, ОС=ОВ та ОА=OD, ч.т.д.
Теорема 13
. Діагоналі рівнобедреної трапеції точкою перетину діляться відповідно рівні відрізки. Розглянемо трикутники АВD та ACD. Вона рівні з двох сторін і куту між ними (АВ=СD, AD - загальна, кути А і D дорівнюють теоремі 10). Тому ∠ ОАD = ∠ ОDA, звідси рівні і кути ОВС і ОСВ як відповідно нахресні для кутів ODA і ОАD. Згадаймо теорему: якщо у трикутнику два кути рівні, то він рівнобедрений, тому трикутники ОВС і ОAD є рівностегновими, отже, ОС=ОВ та ОА=OD, ч.т.д.
Рівнобока трапеція фігура симетрична.
Визначення 13.
Осю сисмметрії рівнобічної трапеції називають пряму, що проходить через середини її основ.
Теорема 14
. Вісь симетрії рівнобічної трапеції перпендикулярна до її підстав. 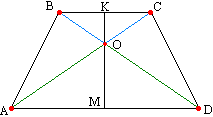 У теоремі 9 ми довели, що пряма, що з'єднує середини основ трапеції, проходить через точку перетину діагоналей. Далі (теорема 13) ми довели, що трикутники АОD та ВОС рівнобедрені. ОМ та ОК є медіанами цих трикутників відповідно за визначенням. Згадаймо властивість рівнобедреного трикутника: медіана рівнобедреного трикутника, опущена на основу, одночасно є і висотою трикутника. Внаслідок перпендикулярності підстав частинам прямої КМ, вісь симетрії перпендикулярна підстав.
У теоремі 9 ми довели, що пряма, що з'єднує середини основ трапеції, проходить через точку перетину діагоналей. Далі (теорема 13) ми довели, що трикутники АОD та ВОС рівнобедрені. ОМ та ОК є медіанами цих трикутників відповідно за визначенням. Згадаймо властивість рівнобедреного трикутника: медіана рівнобедреного трикутника, опущена на основу, одночасно є і висотою трикутника. Внаслідок перпендикулярності підстав частинам прямої КМ, вісь симетрії перпендикулярна підстав.
Ознаки, що виділяють рівнобічну трапецію серед усіх трапецій:
Теорема 15
. Якщо кути, що прилягають до однієї з основ трапеції, рівні, то трапеція рівнобока.
Теорема 16
. Якщо діагоналі трапеції рівні, то трапеція рівнобока.
Теорема 17
. Якщо продовжені до перетину бічні сторони трапеції утворюють разом і її основою рівнобедрений трикутник, то трапеція рівнобока.
Теорема 18
. Якщо трапецію можна вписати в коло, вона рівнобока.
Ознака прямокутної трапеції:
Теорема 19
. Будь-який чотирикутник, у якого лише два кути при суміжних вершинах прямі, є прямокутною трапецією (очевидно, що дві сторони паралельні, тому що односторонні рівні. у випадку, коли три прямі кути це прямокутник)
Теорема 20
. Радіус вписаної в трапецію кола дорівнює половині висоти основи. 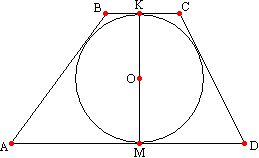 Доказ цієї теореми полягає у поясненні того, що радіуси, проведені до основ, лежать на висоті трапеції. З точки О - центру вписаної в цю трапецію АВСD кола проведемо радіуси в точки торкання її основами трапеції. Як відомо, ридіус, проведений в точку торкання, перпендикулярний до тил, тому ОК^ ВС і ОМ^ AD. Згадаймо теорему: якщо пряма перпендикулярна одній з паралельних прямих, вона перпендикулярна і другий. Отже, пряма ОК також перпендикулярна AD. Таким чином, через точку Проходить дві прямих перпендикулярних прямий AD, чого бути не може, тому ці прямі збігаються і складають загальний перпендикуляр КМ, який дорівнює сумі двох радіусів і є діаметром вписаного кола, тому r=KM/2 або r=h/ 2.
Доказ цієї теореми полягає у поясненні того, що радіуси, проведені до основ, лежать на висоті трапеції. З точки О - центру вписаної в цю трапецію АВСD кола проведемо радіуси в точки торкання її основами трапеції. Як відомо, ридіус, проведений в точку торкання, перпендикулярний до тил, тому ОК^ ВС і ОМ^ AD. Згадаймо теорему: якщо пряма перпендикулярна одній з паралельних прямих, вона перпендикулярна і другий. Отже, пряма ОК також перпендикулярна AD. Таким чином, через точку Проходить дві прямих перпендикулярних прямий AD, чого бути не може, тому ці прямі збігаються і складають загальний перпендикуляр КМ, який дорівнює сумі двох радіусів і є діаметром вписаного кола, тому r=KM/2 або r=h/ 2.
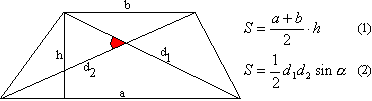
Теорема 21
. Площа трапеції дорівнює добутку напівсуми основ та висоти основ. 
Доведення:Нехай ABCD - це трапеція, а AB і CD - її підстави. Нехай також AH – висота, опущена з точки A на пряму CD. Тоді S ABCD = S ACD + S ABC.
Але S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Отже, S ABCD = 1/2AH · (AB + CD).
Що й потрібно було довести.
 Друга формула перейшла від чотирикутника.
Друга формула перейшла від чотирикутника.
Можливо, буде корисно почитати:
- НТГ – порушення толерантності до глюкози: причини прояву, симптоми та методи корекції;
- Римська імперія. Древній Рим. Римська імперія: прапор, герб, імператори, події Що виникло на місці римської імперії;
- До чого сниться, що хлопець кидає мене;
- Сир філадельфія Домашні рецепти сиру «Філадельфія»;
- Ворожіння на кавовій гущі значення півень;
- Кулемети Росії Калашніков - провідний післявоєнний розробник ссср;
- Гени мітохондріальної днк;
- Сумісність Риб і Риб: безкорислива любов чи нестабільні відносини Сумісність по гороскопу риби немов;
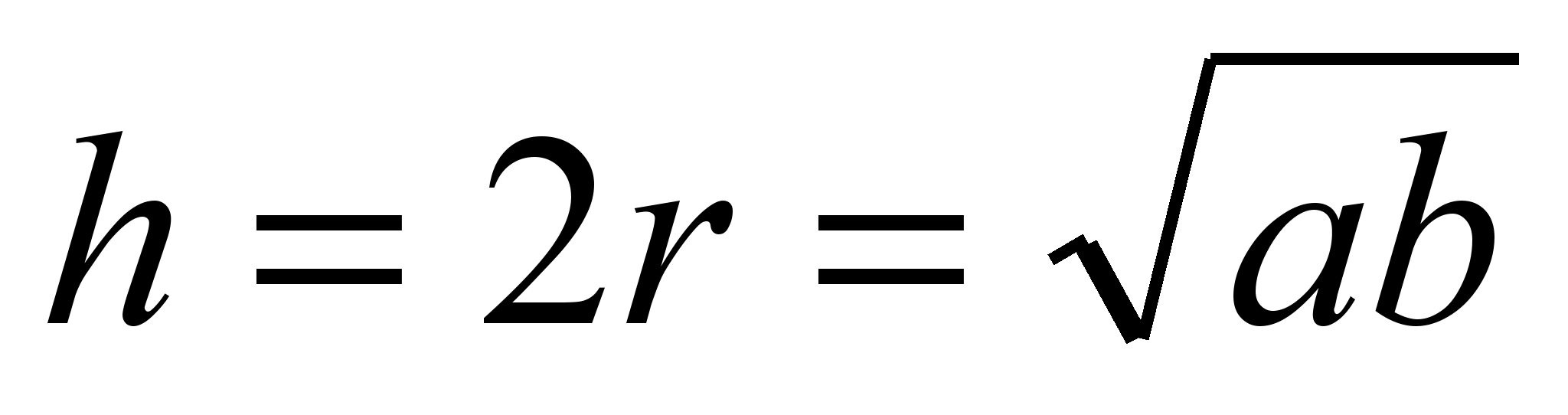 .
.