कॉस अनुपात। सही त्रिकोण। उदाहरणों के साथ विस्तृत सिद्धांत

अनुदेश

विधि 1. पायथागॉरियन प्रमेय का उपयोग करना। प्रमेय कहता है: कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है। यह इस प्रकार है कि एक समकोण त्रिभुज की किसी भी भुजा की गणना उसकी अन्य दो भुजाओं को जानकर की जा सकती है (चित्र 2)।

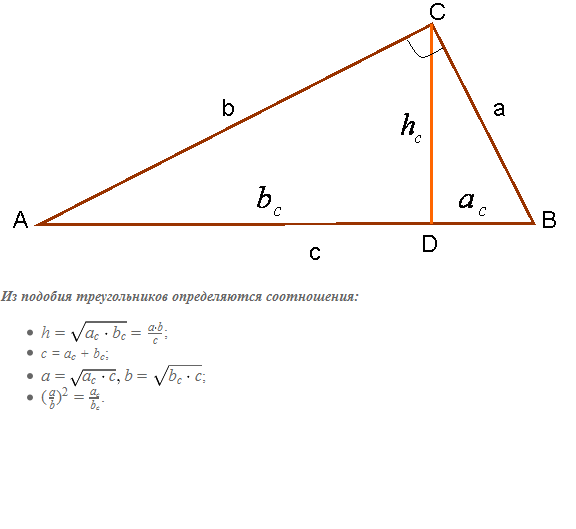
विधि 2। यह इस तथ्य से अनुसरण करता है कि माध्यिका से खींचा गया है समकोणकर्ण के लिए, आपस में 3 समान त्रिभुज बनाते हैं (चित्र 3)। इस आकृति में, त्रिभुज ABC, BCD और ACD समरूप हैं।



कर्ण एक समकोण त्रिभुज में वह भुजा है जो 90 डिग्री के कोण के विपरीत होती है। इसकी लंबाई की गणना करने के लिए, किसी एक पैर की लंबाई और त्रिकोण के तीव्र कोणों में से एक का मान जानना पर्याप्त है।

अनुदेश

एक ज्ञात पैर और समकोण त्रिभुज के एक तीव्र कोण के साथ, कर्ण का आकार इस कोण के कोसाइन / साइन के पैर के अनुपात के बराबर हो सकता है, यदि यह कोण इसके विपरीत / आसन्न है:

h = C1(या C2)/sinα;

h = С1(या С2)/cosα।

उदाहरण: कर्ण AB और समकोण C वाला एक समकोण त्रिभुज ABC दिया है। माना कोण B 60 डिग्री और कोण A 30 डिग्री है। भुजा BC की लंबाई 8 सेमी है। कर्ण AB की लंबाई ज्ञात कीजिए। ऐसा करने के लिए, आप ऊपर सुझाए गए किसी भी तरीके का उपयोग कर सकते हैं:

AB=BC/cos60=8 सेमी.

AB = BC/sin30 = 8 सेमी.

कर्ण एक समकोण त्रिभुज की भुजा है जो समकोण के विपरीत है। यह एक समकोण त्रिभुज की सबसे लंबी भुजा है। आप पाइथागोरस प्रमेय का उपयोग करके या त्रिकोणमितीय कार्यों के सूत्रों का उपयोग करके इसकी गणना कर सकते हैं।

अनुदेश

पैरों को समकोण से सटे समकोण त्रिभुज की भुजाएँ कहा जाता है। आकृति में, पैरों को AB और BC के रूप में नामित किया गया है। दोनों पैरों की लंबाई दी जाए। आइए उन्हें |AB| के रूप में निरूपित करें और |बीसी|। कर्ण |AC| की लंबाई ज्ञात करने के लिए, हम पाइथागोरस प्रमेय का उपयोग करते हैं। इस प्रमेय के अनुसार पादों के वर्गों का योग कर्ण के वर्ग के बराबर होता है, अर्थात् हमारे ड्राइंग के अंकन में |AB|^2 + |BC|^2 = |AC|^2। सूत्र से हम पाते हैं कि कर्ण AC की लंबाई |AC| के रूप में पाई जाती है = √(|एबी|^2 + |बीसी|^2) .

एक उदाहरण पर विचार करें। माना पैरों की लंबाई |AB| = 13, |बीसी| = 21. पाइथागोरस प्रमेय से, हम पाते हैं कि |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610। संख्या 610 से: |AC| = √610। पूर्णांकों के वर्गों की तालिका का उपयोग करके, हम पाते हैं कि संख्या 610 किसी भी पूर्णांक का पूर्ण वर्ग नहीं है। कर्ण की लंबाई का अंतिम मान प्राप्त करने के लिए, आइए मूल चिन्ह के नीचे से एक पूर्ण वर्ग निकालने का प्रयास करें। ऐसा करने के लिए, हम संख्या 610 को कारकों में विघटित करते हैं। 610 = 2 * 5 * 61। तालिका के अनुसार प्रमुख संख्याहम देखते हैं कि 61 एक अभाज्य संख्या है। इसलिए, संख्या √610 को और कम करना असंभव है। हमें अंतिम उत्तर मिलता है |एसी| = √610।
उदाहरण के लिए, यदि कर्ण का वर्ग 675 था, तो √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3। यदि ऐसा कास्ट संभव है, तो एक रिवर्स चेक करें - परिणाम का वर्ग करें और मूल मूल्य के साथ तुलना करें।

आइए हम किसी एक पाद और उससे सटे कोण को जानते हैं। निश्चितता के लिए, इसे पैर |AB| होने दें और कोण α। फिर हम त्रिकोणमितीय फ़ंक्शन कोसाइन के सूत्र का उपयोग कर सकते हैं - कोण का कोसाइन आसन्न पैर के कर्ण के अनुपात के बराबर है। वे। हमारे संकेतन में cos α = |AB| / |एसी|. यहाँ से हमें कर्ण की लंबाई |AC| प्राप्त होती है = |एबी| / cosα।
अगर हम पैर जानते हैं |बीसी | और कोण α, तो हम कोण की ज्या की गणना के लिए सूत्र का उपयोग करते हैं - कोण की ज्या कर्ण के विपरीत पैर के अनुपात के बराबर है: sin α = |BC| / |एसी|. हम पाते हैं कि कर्ण की लंबाई |AC| के रूप में पाई जाती है = |बीसी| / cosα।

स्पष्टता के लिए, एक उदाहरण पर विचार करें। माना पैर की लंबाई |AB| = 15. और कोण α = 60°। हमें मिलता है |AC| = 15 / cos 60° = 15 / 0.5 = 30।
विचार करें कि आप पायथागॉरियन प्रमेय का उपयोग करके अपना परिणाम कैसे देख सकते हैं। ऐसा करने के लिए, हमें दूसरे चरण |BC| की लंबाई की गणना करने की आवश्यकता है। कोण tg α = |BC| की स्पर्शरेखा के लिए सूत्र का उपयोग करना / |AC|, हमें |BC| प्राप्त होता है = |एबी| * टीजी α = 15 * टीजी 60 डिग्री = 15 * √3। इसके बाद, हम पायथागॉरियन प्रमेय लागू करते हैं, हमें 15^2 + (15 * √3)^2 = 30^2 => 225 + 675 = 900 मिलता है। सत्यापन किया जाता है।

मददगार सलाह

कर्ण की गणना करने के बाद, जांचें कि परिणामी मान पाइथागोरस प्रमेय को संतुष्ट करता है या नहीं।

स्रोत:

  • 1 से 10000 तक की अभाज्य संख्याओं की तालिका

पैरएक समकोण त्रिभुज की दो छोटी भुजाओं को नाम दें जो इसके शीर्ष को बनाती हैं, जिसका मान 90 ° है। ऐसे त्रिभुज की तीसरी भुजा कर्ण कहलाती है। त्रिभुज के ये सभी पक्ष और कोण कुछ संबंधों से जुड़े हुए हैं जो आपको कई अन्य पैरामीटर ज्ञात होने पर पैर की लंबाई की गणना करने की अनुमति देते हैं।

अनुदेश

यदि आप समकोण त्रिभुज की अन्य दो भुजाओं (B और C) की लंबाई जानते हैं, तो पैर (A) की लंबाई की गणना करने के लिए पाइथागोरस प्रमेय का उपयोग करें। इस प्रमेय में कहा गया है कि वर्ग पैरों की लंबाई का योग कर्ण के वर्ग के बराबर है। इससे यह पता चलता है कि प्रत्येक पैर की लंबाई कर्ण और दूसरे पैर की लंबाई के वर्गों के बीच के अंतर के वर्गमूल के बराबर है: A=√(C²-B²)।

एक तीव्र कोण के लिए प्रत्यक्ष त्रिकोणमितीय फ़ंक्शन "साइन" की परिभाषा का उपयोग करें, यदि आप परिकलित पैर के विपरीत कोण (α) का मान और कर्ण (C) की लंबाई जानते हैं। यह परिभाषा बताती है कि इस की ज्या ज्ञात कोणकर्ण की लंबाई के लिए वांछित पैर की लंबाई के अनुपात के बराबर। इसका मतलब है कि वांछित पैर की लंबाई कर्ण की लंबाई और ज्ञात कोण की साइन के उत्पाद के बराबर है: A=C∗sin(α)। समान ज्ञात मानों के लिए, आप cosecant फ़ंक्शन की परिभाषा का उपयोग कर सकते हैं और ज्ञात कोण A=C/cosec(α) के cosecant द्वारा कर्ण की लंबाई को विभाजित करके वांछित लंबाई की गणना कर सकते हैं।

प्रत्यक्ष त्रिकोणमितीय फ़ंक्शन कोसाइन की परिभाषा का उपयोग करें, यदि कर्ण (C) की लंबाई के अलावा, वांछित पैर के निकट तीव्र कोण (β) का मान भी ज्ञात हो। इस कोण के कोसाइन को वांछित पैर और कर्ण की लंबाई के अनुपात के रूप में परिभाषित किया गया है, और इससे हम यह निष्कर्ष निकाल सकते हैं कि पैर की लंबाई कर्ण की लंबाई और ज्ञात की कोसाइन के उत्पाद के बराबर है कोण: A=C∗cos(β). आप छेदक फलन की परिभाषा का उपयोग कर सकते हैं और कर्ण की लंबाई को ज्ञात कोण A=C/sec(β) से विभाजित करके वांछित मान की गणना कर सकते हैं।

त्रिकोणमितीय फ़ंक्शन स्पर्शरेखा के व्युत्पन्न के लिए एक समान परिभाषा से आवश्यक सूत्र प्राप्त करें, यदि, तीव्र कोण (α) के मान के अलावा, वांछित पैर (ए) के विपरीत, दूसरे पैर की लंबाई (बी) है ज्ञात। वांछित पैर के विपरीत कोण की स्पर्शरेखा इस पैर की लंबाई से दूसरे पैर की लंबाई का अनुपात है। इसका मतलब है कि वांछित मूल्य ज्ञात पैर की लंबाई और ज्ञात कोण के स्पर्शरेखा के उत्पाद के बराबर होगा: A=B∗tg(α)। इन समान ज्ञात मात्राओं से, कोटैंजेंट फ़ंक्शन की परिभाषा का उपयोग करके एक अन्य सूत्र प्राप्त किया जा सकता है। इस मामले में, पैर की लंबाई की गणना करने के लिए, ज्ञात पैर की लंबाई का अनुपात ज्ञात कोण के कॉटेंजेंट के अनुपात को ढूंढना आवश्यक होगा: ए = बी/सीटीजी (α)।

संबंधित वीडियो

शब्द "केटेट" ग्रीक से रूसी भाषा में आया। सटीक अनुवाद में, इसका अर्थ है एक साहुल रेखा, जो कि पृथ्वी की सतह के लंबवत है। गणित में, पैरों को भुजाएँ कहा जाता है जो एक समकोण त्रिभुज का समकोण बनाती हैं। इस कोण के सम्मुख भुजा कर्ण कहलाती है। "लेग" शब्द का उपयोग आर्किटेक्चर और वेल्डिंग तकनीक में भी किया जाता है।



एक समकोण त्रिभुज ACB खींचिए। इसके पैरों को a और b से लेबल करें, और इसके कर्ण c को लेबल करें। एक समकोण त्रिभुज की सभी भुजाएँ और कोण कुछ संबंधों से जुड़े होते हैं। कर्ण के एक तीव्र कोण के विपरीत पैर के अनुपात को इस कोण की ज्या कहा जाता है। इस त्रिभुज में sinCAB=a/c. कोज्या आसन्न पैर के कर्ण का अनुपात है, यानी cosCAB=b/c। व्युत्क्रम संबंधों को छेदक और व्युत्क्रमज्या कहते हैं।

इस कोण का छेदक कर्ण को सन्निकट पाद से विभाजित करके प्राप्त किया जाता है, अर्थात secCAB=c/b। यह कोसाइन के व्युत्क्रम को दर्शाता है, अर्थात, इसे सूत्र secCAB=1/cosSAB द्वारा व्यक्त किया जा सकता है।
व्युत्क्रमज्या कर्ण को विपरीत पाद से विभाजित करने के भागफल के बराबर होता है और ज्या का व्युत्क्रम होता है। इसकी गणना cosecCAB=1/sinCAB सूत्र का उपयोग करके की जा सकती है

दोनों पैर स्पर्शरेखा और कोटिस्पर्श से जुड़े हुए हैं। में इस मामले मेंस्पर्शरेखा भुजा a से भुजा b का अनुपात होगा, अर्थात, विपरीत पैर आसन्न पैर के लिए। यह अनुपात सूत्र tgCAB=a/b द्वारा व्यक्त किया जा सकता है। तदनुसार, प्रतिलोम अनुपात कोटिस्पर्श होगा: ctgCAB=b/a।

कर्ण और दोनों पैरों के आकार के बीच का अनुपात प्राचीन यूनानी गणितज्ञ पाइथागोरस द्वारा निर्धारित किया गया था। उनके नाम का प्रमेय आज भी लोगों द्वारा प्रयोग किया जाता है। यह कहता है कि कर्ण का वर्ग पैरों के वर्गों के योग के बराबर है, अर्थात c2 \u003d a2 + b2। तदनुसार, प्रत्येक पैर कर्ण और दूसरे पैर के वर्गों के बीच के अंतर के वर्गमूल के बराबर होगा। यह सूत्र b=√(c2-a2) के रूप में लिखा जा सकता है।

पैर की लंबाई को आप जो संबंध जानते हैं, उसके द्वारा भी व्यक्त किया जा सकता है। साइन और कोसाइन के प्रमेय के अनुसार, पैर कर्ण के उत्पाद और इन कार्यों में से एक के बराबर है। इसे स्पर्शरेखा या कोटिस्पर्श के रूप में भी व्यक्त किया जा सकता है। पैर a पाया जा सकता है, उदाहरण के लिए, सूत्र a \u003d b * tan CAB द्वारा। ठीक उसी तरह, दिए गए स्पर्शरेखा या कोटिस्पर्श के आधार पर, दूसरा पैर निर्धारित किया जाता है।

वास्तुकला में, "पैर" शब्द का भी प्रयोग किया जाता है। यह एक आयनिक राजधानी पर लागू होता है और इसकी पीठ के मध्य के माध्यम से एक साहुल रेखा को दर्शाता है। अर्थात्, इस मामले में, यह शब्द किसी दी गई रेखा के लंब को दर्शाता है।

वेल्डिंग तकनीक में, "लेग फिलेट वेल्ड" की अवधारणा है। अन्य मामलों की तरह, यह सबसे छोटी दूरी है। यहाँ हम बात कर रहे हैंदूसरे भाग की सतह पर स्थित सीम की सीमा तक वेल्ड किए जाने वाले भागों में से एक के बीच की खाई के बारे में।

संबंधित वीडियो

स्रोत:

  • पैर और कर्ण क्या है

संबंधित वीडियो

टिप्पणी

एक समकोण त्रिभुज की भुजाओं की गणना करते समय, इसकी विशेषताओं का ज्ञान खेल सकता है:
1) यदि एक समकोण का पाद 30 डिग्री के कोण के विपरीत स्थित है, तो यह कर्ण के आधे के बराबर है;
2) कर्ण हमेशा किसी भी टांग से लंबा होता है;
3) यदि एक वृत्त एक समकोण त्रिभुज के चारों ओर परिचालित है, तो इसका केंद्र कर्ण के मध्य में स्थित होना चाहिए।

त्रिकोणमिति गणित की एक शाखा है जो त्रिकोणमितीय कार्यों का अध्ययन करती है, साथ ही अभ्यास में उनका उपयोग भी करती है। इन सुविधाओं में शामिल हैं साइनस, कोज्या, स्पर्शरेखा और कोटिस्पर्श।

साइनस है त्रिकोणमितीय समारोह , कर्ण के परिमाण के विपरीत पैर के परिमाण का अनुपात।

त्रिकोणमिति में साइन।

जैसा कि ऊपर उल्लेख किया गया है, ज्या सीधे त्रिकोणमिति और त्रिकोणमितीय कार्यों से संबंधित है। इसका कार्य द्वारा निर्धारित किया जाता है

  • कोण की गणना करने में मदद करें, बशर्ते कि त्रिभुज की भुजाओं के आयाम ज्ञात हों;
  • त्रिभुज की भुजा के आकार की गणना करने में मदद करें, बशर्ते कि कोण ज्ञात हो।

यह याद रखना चाहिए कि त्रिकोण के किसी भी आकार के लिए साइन का मान हमेशा समान रहेगा, क्योंकि साइन माप नहीं है, बल्कि एक अनुपात है।

नतीजतन, किसी विशेष समस्या के प्रत्येक समाधान के लिए इस निरंतर मूल्य की गणना नहीं करने के लिए, विशेष त्रिकोणमितीय तालिकाओं का निर्माण किया गया। इनमें ज्या, कोज्या, स्पर्शरेखा और कोटिस्पर्श के मान पहले ही परिकलित और नियत किए जा चुके हैं। आमतौर पर ये तालिकाएँ बीजगणित और ज्यामिति की पाठ्यपुस्तकों के मुख पृष्ठ पर दी जाती हैं। उन्हें इंटरनेट पर भी पाया जा सकता है।

ज्यामिति में साइन।

ज्यामिति को कल्पना की आवश्यकता होती है, इसलिए व्यवहार में समझने के लिए, एक कोण की ज्या क्या है, आपको समकोण के साथ एक त्रिभुज बनाने की आवश्यकता है।

आइए मान लें कि एक समकोण बनाने वाली भुजाओं का नाम दिया गया है एसी,विपरीत कोण एक्स.

आमतौर पर कार्यों में पक्षों की लंबाई का संकेत दिया जाता है। हम कहते हैं ए = 3, बी = 4. इस मामले में, पहलू अनुपात ¾ जैसा दिखेगा। इसके अलावा, यदि हम तीव्र कोण से सटे त्रिभुज की भुजाओं को लंबा करते हैं एक्स, तब भुजाएँ बढ़ेंगी एऔर वी, और कर्ण एक समकोण त्रिभुज की तीसरी भुजा है जो आधार के समकोण पर नहीं है। अब त्रिभुज की भुजाओं को अलग तरह से कहा जा सकता है, उदाहरण के लिए: एम, एन, के।

इस संशोधन के साथ, त्रिकोणमिति के नियम ने काम किया: त्रिभुज की भुजाओं की लंबाई बदल गई, लेकिन उनका अनुपात नहीं बदला।

तथ्य यह है कि यदि आप किसी त्रिभुज की भुजाओं की लंबाई को जितनी बार चाहें बदल सकते हैं और कोण x के मान को बनाए रखते हुए, इसके पक्षों के बीच का अनुपात अभी भी अपरिवर्तित रहेगा, प्राचीन वैज्ञानिकों ने देखा। हमारे मामले में, भुजाओं की लंबाई इस प्रकार बदल सकती है: ए / बी \u003d ¾, जब पक्ष लंबा हो जाता है ए 6 सेमी तक, और वी- 8 सेमी तक हमें मिलता है: एम/एन = 6/8 = 3/4.

इस संबंध में एक समकोण त्रिभुज में भुजाओं के अनुपात को कहा जाता है:

  • कोण x का साइन कर्ण के विपरीत पैर का अनुपात है: sinx = a/c;
  • कोण x का कोज्या कर्ण के सन्निकट पैर का अनुपात है: cosx = w/s;
  • कोण x का स्पर्शरेखा आसन्न पैर के विपरीत पैर का अनुपात है: tgx \u003d a / b;
  • कोण x का स्पर्शरेखा आसन्न पैर के विपरीत एक का अनुपात है: ctgx \u003d in / a।

हम त्रिकोणमिति के अपने अध्ययन की शुरुआत एक समकोण त्रिभुज से करते हैं। आइए परिभाषित करें कि साइन और कोसाइन क्या हैं, साथ ही एक तीव्र कोण के स्पर्शरेखा और कोटिस्पर्श। ये त्रिकोणमिति की मूल बातें हैं।

याद करें कि समकोणके बराबर कोण है। दूसरे शब्दों में, अनफोल्डेड कॉर्नर का आधा।

तेज़ कोने- छोटा।

अधिक कोण- बड़ा। ऐसे कोण के संबंध में, "कुंद" अपमान नहीं है, बल्कि एक गणितीय शब्द है :-)


आइए एक समकोण त्रिभुज बनाएँ। एक समकोण को आमतौर पर निरूपित किया जाता है। ध्यान दें कि कोने के विपरीत पक्ष को एक ही अक्षर से दर्शाया जाता है, केवल छोटा। अतः, कोण के विपरीत स्थित भुजा को निरूपित किया जाता है।

एक कोण को संबंधित ग्रीक अक्षर द्वारा निरूपित किया जाता है।

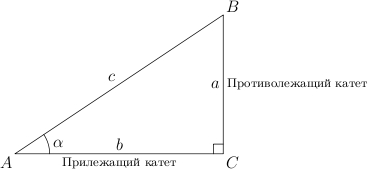
कर्णएक समकोण त्रिभुज समकोण के विपरीत भुजा है।

पैर- तेज कोनों के विपरीत पक्ष।

कोने के विपरीत पैर कहा जाता है विलोम(कोण के सापेक्ष)। दूसरा पैर, जो कोने के एक तरफ स्थित होता है, कहलाता है नज़दीक.

साइनसएक समकोण त्रिभुज में तीव्र कोण सम्मुख भुजा का कर्ण से अनुपात होता है:

कोज्याएक समकोण त्रिभुज में तीव्र कोण - कर्ण के निकटवर्ती पैर का अनुपात:

स्पर्शरेखाएक समकोण त्रिभुज में तीव्र कोण - विपरीत पैर के आसन्न का अनुपात:

एक अन्य (समतुल्य) परिभाषा: एक तीव्र कोण की स्पर्शरेखा एक कोण की ज्या का उसके कोज्या से अनुपात है:

स्पर्शरेखाएक समकोण त्रिभुज में तीव्र कोण - आसन्न पैर का अनुपात विपरीत (या, समतुल्य, कोसाइन से साइन का अनुपात):

साइन, कोसाइन, टेंगेंट और कोटेन्जेंट के मूल अनुपातों पर ध्यान दें, जो नीचे दिए गए हैं। वे समस्याओं को हल करने में हमारे लिए उपयोगी होंगे।


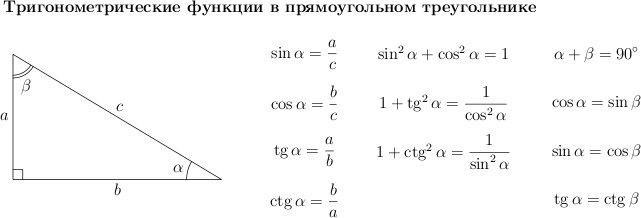
आइए उनमें से कुछ को सिद्ध करें।

1. किसी त्रिभुज के कोणों का योग होता है। साधन, एक समकोण त्रिभुज के दो न्यून कोणों का योग होता है .

2. एक ओर, विपरीत पैर के कर्ण के अनुपात के रूप में। दूसरी ओर, चूंकि कोण के लिए पैर सटे होंगे।

हमें वह मिल गया . दूसरे शब्दों में, ।

3. पायथागॉरियन प्रमेय लें: . आइए दोनों भागों को इस प्रकार विभाजित करें:

हमें मिला बुनियादी त्रिकोणमितीय पहचान:

इस प्रकार, कोण की ज्या जानने के बाद, हम इसके कोसाइन और इसके विपरीत पता लगा सकते हैं।

4. मुख्य त्रिकोणमितीय पहचान के दोनों भागों को से विभाजित करने पर, हम प्राप्त करते हैं:

इसका मतलब यह है कि अगर हमें एक तीव्र कोण की स्पर्शरेखा दी गई है, तो हम तुरंत इसकी कोज्या पा सकते हैं।

वैसे ही,

ठीक है, हमने परिभाषाएँ और लिखित सूत्र दिए हैं। लेकिन हमें साइन, कोसाइन, टेंगेंट और कॉटैंजेंट की आवश्यकता क्यों है?

हम वह जानते हैं किसी त्रिभुज के कोणों का योग होता है.

हम के बीच संबंध जानते हैं दलोंसही त्रिकोण। यह पाइथागोरस प्रमेय है: .

यह पता चला है कि एक त्रिभुज में दो कोणों को जानने के बाद, आप तीसरे का पता लगा सकते हैं। एक समकोण त्रिभुज में दो भुजाएँ जानने पर आप तीसरी ज्ञात कर सकते हैं। तो, कोणों के लिए - उनका अनुपात, पक्षों के लिए - उनका अपना। लेकिन क्या करें यदि एक समकोण त्रिभुज में एक कोण (एक समकोण को छोड़कर) और एक भुजा ज्ञात हो, लेकिन आपको अन्य भुजाएँ खोजने की आवश्यकता है?

प्रारंभ में, साइन और कोसाइन समकोण त्रिभुजों में राशियों की गणना करने की आवश्यकता के कारण उत्पन्न हुए। यह देखा गया कि यदि एक समकोण त्रिभुज में कोणों के डिग्री माप का मान नहीं बदला जाता है, तो पक्षानुपात, इन भुजाओं की लंबाई में कितना भी परिवर्तन क्यों न हो, हमेशा समान रहता है।

इस तरह साइन और कोसाइन की अवधारणाओं को पेश किया गया। एक समकोण त्रिभुज में एक तीव्र कोण की साइन कर्ण के विपरीत पैर का अनुपात है, और कोज्या कर्ण के निकटवर्ती पैर का अनुपात है।

कोसाइन और साइन के प्रमेय

लेकिन कोसाइन और साइन का उपयोग न केवल समकोण त्रिभुजों में किया जा सकता है। किसी त्रिभुज की भुजा, अधिक कोण या तीव्र कोण का मान ज्ञात करने के लिए, कोसाइन और साइन प्रमेय को लागू करना पर्याप्त है।

कोसाइन प्रमेय काफी सरल है: "त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है, जो इन भुजाओं के बीच के कोण के कोसाइन द्वारा इन भुजाओं के उत्पाद का दोगुना होता है।"

साइन प्रमेय की दो व्याख्याएँ हैं: छोटी और विस्तारित। छोटे के अनुसार: "त्रिभुज में, कोण विपरीत पक्षों के समानुपाती होते हैं।" इस प्रमेय को अक्सर त्रिभुज के चारों ओर वर्णित चक्र की संपत्ति के कारण विस्तारित किया जाता है: "त्रिभुज में, कोण विपरीत पक्षों के समानुपाती होते हैं, और उनका अनुपात परिधि वाले चक्र के व्यास के बराबर होता है।"

संजात

एक व्युत्पन्न एक गणितीय उपकरण है जो दिखाता है कि तर्क में बदलाव के संबंध में फ़ंक्शन कितनी जल्दी बदलता है। डेरिवेटिव का उपयोग बीजगणित, ज्यामिति, अर्थशास्त्र और भौतिकी, कई तकनीकी विषयों में किया जाता है।

समस्याओं को हल करते समय, आपको त्रिकोणमितीय कार्यों के डेरिवेटिव के सारणीबद्ध मूल्यों को जानना होगा: साइन और कोसाइन। साइन का व्युत्पन्न कोसाइन है, और कोसाइन का व्युत्पन्न साइन है, लेकिन माइनस साइन के साथ।

गणित में आवेदन

विशेष रूप से अक्सर साइन और कोसाइन का उपयोग सही त्रिकोण और उनसे संबंधित समस्याओं को हल करने के लिए किया जाता है।

ज्या और कोज्या की सुविधा प्रौद्योगिकी में भी परिलक्षित होती है। कोसाइन और साइन प्रमेयों का उपयोग करके कोणों और पक्षों का मूल्यांकन करना आसान था, जटिल आकृतियों और वस्तुओं को "सरल" त्रिकोणों में तोड़ना। इंजीनियरों और आर्किटेक्ट्स, अक्सर पहलू अनुपात और डिग्री उपायों की गणना से निपटते हैं, गैर-टेबल कोणों के कोसाइन और साइन की गणना करने में बहुत समय और प्रयास करते हैं।

तब ब्रैडिस टेबल बचाव के लिए आए, जिसमें विभिन्न कोणों के साइन, कोसाइन, स्पर्शरेखा और कोटिस्पर्श के हजारों मूल्य थे। में सोवियत समयकुछ शिक्षकों ने अपने छात्रों को ब्रैडी टेबल के पन्नों को याद करने के लिए मजबूर किया।

एक समकोण त्रिभुज पर, सबसे सरल बहुभुज के रूप में, विभिन्न पंडितों ने उन दिनों में त्रिकोणमिति के क्षेत्र में अपने ज्ञान का सम्मान किया जब किसी ने भी गणित के इस क्षेत्र को उस शब्द से नहीं बुलाया। इसलिए, आज उस लेखक को इंगित करना संभव नहीं है जिसने इस सपाट ज्यामितीय आकृति में पक्षों की लंबाई और कोणों के परिमाण के अनुपात में पैटर्न का खुलासा किया। ऐसे संबंधों को त्रिकोणमितीय कार्य कहा जाता है और कई समूहों में विभाजित किया जाता है, जिनमें से मुख्य को पारंपरिक रूप से "प्रत्यक्ष" कार्य माना जाता है। इस समूह को केवल दो कार्य सौंपे गए हैं, और उनमें से एक साइन है।

अनुदेश

परिभाषा के अनुसार, एक समकोण त्रिभुज में एक कोण 90° के बराबर होता है, और इस तथ्य के कारण कि यूक्लिडियन ज्यामिति में इसके कोणों का योग 180° के बराबर होना चाहिए, अन्य दो कोण तीव्र होते हैं (अर्थात 90° से कम) ). ठीक इन कोणों और भुजाओं की लंबाई के अनुपातों की नियमितता त्रिकोणमितीय कार्यों का वर्णन करती है।

फ़ंक्शन, जिसे न्यूनकोण की ज्या कहा जाता है, एक समकोण त्रिभुज की दो भुजाओं की लंबाई के बीच के अनुपात को निर्धारित करता है, जिनमें से एक इस तीव्र कोण के विपरीत स्थित है, और दूसरा इसके समीप है और समकोण के विपरीत स्थित है। चूंकि इस तरह के त्रिकोण में समकोण के विपरीत पक्ष को कर्ण कहा जाता है, और अन्य दो पैर हैं, साइन फ़ंक्शन की परिभाषा को विपरीत पैर की लंबाई और कर्ण के बीच के अनुपात के रूप में तैयार किया जा सकता है।

इस त्रिकोणमितीय फ़ंक्शन की इतनी सरल परिभाषा के अलावा, आज और भी जटिल हैं: कार्टेशियन निर्देशांक में एक सर्कल के माध्यम से, श्रृंखला के माध्यम से, अंतर और कार्यात्मक समीकरणों के समाधान के माध्यम से। यह कार्य निरंतर है, अर्थात, इसके तर्क ("परिभाषाओं का डोमेन") कोई भी संख्या हो सकती है - असीम रूप से नकारात्मक से असीम रूप से सकारात्मक। और इस फ़ंक्शन के अधिकतम और न्यूनतम मान -1 से +1 तक सीमित हैं - यह "इसके मूल्यों की सीमा" है। ज्या अपना न्यूनतम मान 270° के कोण पर लेती है, जो पाई के 3/2 से मेल खाती है, और अधिकतम 90° (पाई का आधा) पर प्राप्त होता है। 0°, 180°, 360°, आदि पर फलन मान शून्य हो जाते हैं। इस सब से यह पता चलता है कि ज्या एक आवधिक कार्य है और इसकी अवधि 360 ° या दो बार संख्या पाई के बराबर है।

किसी दिए गए तर्क से इस फ़ंक्शन के मानों की व्यावहारिक गणना के लिए, आप कैलकुलेटर का उपयोग कर सकते हैं - उनमें से अधिकांश (सॉफ़्टवेयर कैलकुलेटर सहित) ऑपरेटिंग सिस्टमआपका कंप्यूटर) के पास संबंधित विकल्प है।

संबंधित वीडियो

अनुदेश

कोनाएक समकोण त्रिभुज में, आपको कोसाइन की परिभाषा का उपयोग करने की आवश्यकता है और आसन्न पैर का कर्ण से अनुपात ज्ञात करना है:
क्योंकि? = ए/सी, जहां ए पैर की लंबाई है, सी कर्ण की लंबाई है।

यदि आपको कोज्या खोजने की आवश्यकता है कोनामनमानी त्रिभुज में, कोसाइन प्रमेय का उपयोग करना आवश्यक है:
अगर कोण तीव्र है: कॉस? = (ए2 + बी2 - सी2)/(2एबी);
अगर कोण अधिक है: क्योंकि? = (c2 - a2 - b2)/(2ab), जहां a, b कोने से सटी भुजाओं की लंबाई है, c कोने के विपरीत भुजा की लंबाई है।

यदि आपको कोज्या खोजने की आवश्यकता है कोनाएक मनमानी ज्यामितीय आकृति में, मूल्य निर्धारित करना आवश्यक है कोनाडिग्री या रेडियन में, और कोज्या कोनाएक इंजीनियरिंग कैलकुलेटर, ब्रैडिस टेबल, या किसी अन्य गणितीय अनुप्रयोग का उपयोग करके इसके परिमाण का पता लगाएं।

कोज्याकोण का मूल त्रिकोणमितीय कार्य है। विभिन्न अक्षों पर वैक्टर के अनुमानों का निर्धारण करते समय कोसाइन निर्धारित करने की क्षमता वेक्टर बीजगणित में उपयोगी होती है।

अनुदेश

cos?=(b?+c?-a?)/(2*b*c)

एक त्रिभुज है जिसकी भुजाएँ a, b, c क्रमशः 3, 4, 5 मिमी के बराबर हैं।

पाना कोज्याबड़े पक्षों के बीच संलग्न कोण।

आइए हम भुजा के विपरीत कोण को a से निरूपित करें?, फिर, ऊपर दिए गए सूत्र के अनुसार, हमारे पास है:

cos?=(b?+c?-a?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 =32/40=0.8

उत्तर: 0.8।

यदि त्रिभुज एक समकोण त्रिभुज है, तो ज्ञात करना है कोज्याऔर यह कोण की किन्हीं दो भुजाओं की लंबाई जानने के लिए पर्याप्त है ( कोज्यासमकोण 0 है)।

माना भुजाओं a, b, c के साथ एक समकोण त्रिभुज है, जहाँ c कर्ण है।

सभी विकल्पों पर विचार करें:

cos ज्ञात करें? यदि भुजाओं a और b की लंबाई ज्ञात हो (त्रिकोण के पैर)

आइए अतिरिक्त रूप से पाइथागोरस प्रमेय का उपयोग करें:

cos?=(b?+c?-a?)/(2*b*c)=(b?+b?+a?-a?)/(2*b*v(b?+a?)) =(2*b?)/(2*b*v(b?+a?))=b/v(b?+a?)

परिणामी सूत्र की शुद्धता की जांच करने के लिए, हम इसमें उदाहरण 1 के मानों को प्रतिस्थापित करते हैं, अर्थात।

प्रारंभिक गणना करने के बाद, हम प्राप्त करते हैं:

इसी प्रकार, है कोज्याएक आयताकार में त्रिकोणअन्य मामलों में:

ज्ञात ए और सी (कर्ण और विपरीत पैर), कॉस खोजें?

cos?=(b?+c?-a?)/(2*b*c)=(c?-a?+c?-a?)/(2*c*v(c?-a?)) =(2*s?-2*a?)/(2*s*v(s?-a?))=v(s?-a?)/s.

पहले उदाहरण से मूल्यों a=3 और c=5 को प्रतिस्थापित करते हुए, हम प्राप्त करते हैं:

बी और सी ज्ञात हैं (कर्ण और आसन्न पैर)।

एसओएस खोजें?

समान परिवर्तन करने के बाद (उदाहरण 2 और 3 में दिखाया गया है), हम इस मामले में प्राप्त करते हैं कोज्यावी त्रिकोणएक बहुत ही सरल सूत्र का उपयोग करके गणना की गई:

व्युत्पन्न सूत्र की सादगी को प्राथमिक रूप से समझाया गया है: वास्तव में, कोने से सटे? पैर कर्ण का एक प्रक्षेपण है, इसलिए इसकी लंबाई कर्ण की लंबाई को कॉस से गुणा करने के बराबर है।

मूल्यों को प्रतिस्थापित करना b=4 तथा c=5 पहले उदाहरण से, हम प्राप्त करते हैं:

तो हमारे सभी सूत्र सही हैं।

टिप 5: एक समकोण त्रिभुज में न्यूनकोण कैसे ज्ञात करें

सीधे कोयला कात्रिभुज शायद सबसे प्रसिद्ध में से एक है, ऐतिहासिक दृष्टि से, ज्यामितीय आकार. पायथागॉरियन "पैंट" केवल "यूरेका!" आर्किमिडीज।



आपको चाहिये होगा

  • - एक त्रिकोण का आरेखण;
  • - शासक;
  • - चाँदा।

अनुदेश

त्रिभुज के कोणों का योग 180 डिग्री होता है। एक आयताकार में त्रिकोणएक कोण (दाहिना) हमेशा 90 डिग्री का होगा, और शेष न्यूनकोण हैं, अर्थात प्रत्येक 90 डिग्री से कम। एक आयताकार में कौन सा कोण निर्धारित करने के लिए त्रिकोणसीधा है, एक रूलर से त्रिभुज की भुजाओं को मापें और सबसे बड़ा निर्धारित करें। इसे कर्ण (AB) कहा जाता है और समकोण (C) के विपरीत होता है। शेष दो भुजाएँ एक समकोण बनाती हैं और उन्हें पैर (AC, BC) कहा जाता है।

एक बार जब आप यह निर्धारित कर लेते हैं कि कौन सा कोण तीव्र है, तो आप या तो कोण को प्रोट्रैक्टर से माप सकते हैं या गणितीय सूत्रों का उपयोग करके इसकी गणना कर सकते हैं।

प्रोट्रैक्टर का उपयोग करके कोण के मान को निर्धारित करने के लिए, इसके शीर्ष को संरेखित करें (चलिए इसे अक्षर A से निरूपित करते हैं) प्रोट्रैक्टर के केंद्र में शासक पर एक विशेष चिह्न के साथ, AC पैर को इसके ऊपरी किनारे के साथ मेल खाना चाहिए। चाँदे के अर्धवृत्ताकार भाग पर वह बिंदु अंकित करें जहाँ से कर्ण AB गुजरता है। इस बिंदु पर मान डिग्री में कोण मान से मेल खाता है। यदि प्रोट्रैक्टर पर 2 मान इंगित किए जाते हैं, तो एक तीव्र कोण के लिए आपको एक छोटे से एक को चुनने की आवश्यकता होती है, एक कुंद के लिए - एक बड़ा।

ब्रैडिस संदर्भ तालिकाओं में परिणामी मान ज्ञात करें और निर्धारित करें कि कौन सा कोण प्राप्त से मेल खाता है अंकीय मूल्य. हमारी दादी-नानी इस पद्धति का उपयोग करती थीं।

आजकल, त्रिकोणमितीय सूत्रों की गणना के कार्य के साथ कैलकुलेटर लेना पर्याप्त है। उदाहरण के लिए, अंतर्निहित विंडोज कैलकुलेटर। "कैलकुलेटर" एप्लिकेशन लॉन्च करें, "देखें" मेनू आइटम में, "इंजीनियरिंग" आइटम चुनें। वांछित कोण की साइन की गणना करें, उदाहरण के लिए, sin (A) = BC/AB = 2/4 = 0.5

कैलकुलेटर डिस्प्ले पर INV बटन पर क्लिक करके कैलकुलेटर को इनवर्स फंक्शन मोड में स्विच करें, फिर आर्क्साइन फ़ंक्शन की गणना के लिए बटन पर क्लिक करें (डिस्प्ले पर माइनस फर्स्ट डिग्री के लिए पाप के रूप में चिह्नित)। गणना विंडो में निम्नलिखित शिलालेख दिखाई देगा: asind (0.5) = 30. यानी, वांछित कोण 30 डिग्री है।

स्रोत:

  • ब्रैडिस टेबल (साइन, कोसाइन)

गणित में कोसाइन प्रमेय का सबसे अधिक उपयोग तब किया जाता है जब एक कोण और दो भुजाओं द्वारा तीसरी भुजा ज्ञात करना आवश्यक होता है। हालाँकि, कभी-कभी समस्या की स्थिति इसके विपरीत होती है: दी गई तीन भुजाओं के लिए कोण ज्ञात करना आवश्यक होता है।



अनुदेश

कल्पना कीजिए कि आपको दो भुजाओं की ज्ञात लंबाई और एक कोण के मान वाला एक त्रिभुज दिया गया है। इस त्रिभुज के सभी कोण एक दूसरे के बराबर नहीं हैं, और इसकी भुजाएँ भी आकार में भिन्न हैं। कोण γ त्रिभुज की भुजा के विपरीत स्थित है, जिसे AB के रूप में निर्दिष्ट किया गया है, जो इस आकृति का आधार है। इस कोण के माध्यम से, साथ ही शेष भुजाओं एसी और बीसी के माध्यम से, आप कोज्या प्रमेय का उपयोग करके त्रिभुज की उस भुजा को पा सकते हैं, जो अज्ञात है, इसके आधार पर नीचे दिए गए सूत्र को प्राप्त करें:
a^2=b^2+c^2-2bc*cosγ, कहा पे a=BC, b=AB, c=AC
कोसाइन प्रमेय को अन्यथा सामान्यीकृत पाइथागोरस प्रमेय कहा जाता है।

 

इसे पढ़ना उपयोगी हो सकता है: