ფუნქციები სეგმენტზე. ფუნქციის უწყვეტობა ინტერვალზე და სეგმენტზე
ფუნქციების თვისებები, რომლებიც უწყვეტია ინტერვიუზე
განვიხილოთ ფუნქციების ზოგიერთი თვისება უწყვეტი ინტერვალზე. ჩვენ წარმოგიდგენთ ამ თვისებებს მტკიცებულების გარეშე.
ფუნქცია y = f(x)დაურეკა უწყვეტი სეგმენტზე [ა, ბ], თუ იგი უწყვეტია ამ სეგმენტის ყველა შიდა წერტილში და მის ბოლოებზე, ე.ი. წერტილებში ადა ბ, უწყვეტია მარჯვნივ და მარცხნივ, შესაბამისად.
თეორემა 1.უწყვეტი ფუნქცია ინტერვალზე [ ა, ბ], ამ სეგმენტის ერთ წერტილს მაინც იღებს უმაღლესი ღირებულებადა ერთში მაინც – ყველაზე ნაკლებად.
თეორემა ამბობს, რომ თუ ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ], მაშინ არის მინიმუმ ერთი წერტილი x 1 Î [ ა, ბ] ისეთი, რომ ფუნქციის მნიშვნელობა f(x)ამ ეტაპზე იქნება ყველაზე დიდი მისი ყველა მნიშვნელობიდან ამ სეგმენტზე: f(x 1) ≥ f(x). ანალოგიურად, არსებობს ასეთი წერტილი x 2, რომელშიც ფუნქციის მნიშვნელობა იქნება სეგმენტის ყველა მნიშვნელობიდან ყველაზე პატარა: f(x 1) ≤ f(x).
ნათელია, რომ შეიძლება იყოს რამდენიმე ასეთი წერტილი, მაგალითად, ფიგურა აჩვენებს, რომ ფუნქცია f(x)იღებს უმცირესი ღირებულებაორ წერტილში x 2და x 2 ".
კომენტარი. თეორემის განცხადება შეიძლება არასწორი გახდეს, თუ გავითვალისწინებთ ფუნქციის მნიშვნელობას ინტერვალზე ( ა, ბ). მართლაც, თუ გავითვალისწინებთ ფუნქციას y = x(0, 2), მაშინ ის უწყვეტია ამ ინტერვალზე, მაგრამ არ აღწევს მასში არც უდიდეს და არც უმცირეს მნიშვნელობებს: ის აღწევს ამ მნიშვნელობებს ინტერვალის ბოლოებში, მაგრამ ბოლოები არ ეკუთვნის. ჩვენს დომენზე.
ასევე, თეორემა წყვეტს ჭეშმარიტებას უწყვეტი ფუნქციებისთვის. მიეცი მაგალითი.
შედეგი.თუ ფუნქცია f(x)უწყვეტია [ ა, ბ], მაშინ ის შეზღუდულია ამ სეგმენტზე.
თეორემა 2.დაუშვით ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ] და ამ სეგმენტის ბოლოებში იღებს სხვადასხვა ნიშნის მნიშვნელობებს, მაშინ სეგმენტის შიგნით არის მინიმუმ ერთი წერტილი x = C, რომელშიც ფუნქცია მიდის ნულზე: f(C)= 0, სადაც a< C< b
ამ თეორემას აქვს მარტივი გეომეტრიული მნიშვნელობა: თუ უწყვეტი ფუნქციის გრაფიკის წერტილები y = f(x)სეგმენტის ბოლოების შესაბამისი [ ა, ბ] წოლა გასწვრივ სხვადასხვა მხარეებიღერძიდან ოქსი, მაშინ ეს გრაფიკი კვეთს ღერძს სეგმენტის ერთ წერტილში მაინც ოქსი. უწყვეტ ფუნქციებს შეიძლება არ ჰქონდეს ეს თვისება.
ეს თეორემა აღიარებს შემდეგ განზოგადებას.
თეორემა 3 (შუალედური ღირებულების თეორემა).დაუშვით ფუნქცია y = f(x)არის უწყვეტი ინტერვალზე [ ა, ბ] და f(a) = A, f(b) = B. შემდეგ ნებისმიერი ნომრისთვის Cშორის დადებული ადა ბამ სეგმენტის შიგნით არის ასეთი წერტილი CÎ [ ა, ბ], Რა f(c) = C.
ეს თეორემა გეომეტრიულად აშკარაა. განვიხილოთ ფუნქციის გრაფიკი y = f(x). დაე f(a) = A, f(b) = B. შემდეგ ნებისმიერი სწორი ხაზი y = C, სად C- ნებისმიერი რიცხვი შორის ადა ბ, ერთ წერტილში მაინც გადაკვეთს ფუნქციის გრაფიკს. გადაკვეთის წერტილის აბსცისა იქნება ეს მნიშვნელობა x = C, რომელიც f(c) = C.
ამრიგად, უწყვეტი ფუნქცია, რომელიც გადადის ერთი მნიშვნელობიდან მეორეზე, აუცილებლად გადის ყველა შუალედურ მნიშვნელობას. Კერძოდ:
შედეგი.თუ ფუნქცია y = f(x)არის უწყვეტი გარკვეული ინტერვალით და იღებს უდიდეს და უმცირეს მნიშვნელობებს, შემდეგ ამ ინტერვალზე ერთხელ მაინც იღებს ნებისმიერ მნიშვნელობას, რომელიც შეიცავს მის უმცირეს და უდიდეს მნიშვნელობებს შორის.
წარმოებული და მისი აპლიკაციები. წარმოებულის განმარტება
მოდით, გარკვეული ფუნქცია გვქონდეს y=f(x),განსაზღვრულია გარკვეული ინტერვალით. თითოეული არგუმენტის მნიშვნელობისთვის xამ ინტერვალიდან ფუნქცია y=f(x)აქვს გარკვეული მნიშვნელობა.
განვიხილოთ ორი არგუმენტის მნიშვნელობა: საწყისი x 0 და ახალი x.
განსხვავება x–x 0 ეწოდება x არგუმენტის გაზრდითწერტილში x 0 და აღინიშნება Δx. ამრიგად, Δx = x – x 0 (არგუმენტის ზრდა შეიძლება იყოს დადებითი ან უარყოფითი). ამ თანასწორობიდან გამომდინარეობს, რომ x=x 0 +Δx, ე.ი. ცვლადის საწყისმა მნიშვნელობამ მიიღო გარკვეული ზრდა. მაშინ, თუ წერტილში x 0 ფუნქციის მნიშვნელობა იყო f(x 0 ), შემდეგ ახალ წერტილში xფუნქცია მიიღებს მნიშვნელობას f(x) = f(x 0 +Δx).
განსხვავება წ–წ 0 = f(x) – f(x 0 ) დაურეკა ფუნქციის ზრდა y = f(x)წერტილში x 0 და მითითებულია სიმბოლოთი Δy. ამრიგად,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
როგორც წესი, არგუმენტის საწყისი მნიშვნელობა x 0 ითვლება ფიქსირებულად, ხოლო ახალი მნიშვნელობა x- ცვლადი. მაშინ წ 0 = f(x 0 ) მუდმივი გამოდის და y = f(x)- ცვლადი. მატება Δyდა Δxასევე იქნება ცვლადები და ფორმულა (1) აჩვენებს, რომ Dyარის ცვლადის ფუნქცია Δx.
შევქმნათ ფუნქციის ზრდის შეფარდება არგუმენტის ზრდასთან
მოდით ვიპოვოთ ამ თანაფარდობის ზღვარი ზე Δx→0. თუ ეს ზღვარი არსებობს, მაშინ მას ამ ფუნქციის წარმოებული ეწოდება f(x)წერტილში x 0 და აღნიშნეთ ვ "(x 0). Ისე,
წარმოებულიამ ფუნქციას y = f(x)წერტილში x 0 ეწოდება Δ ფუნქციის ზრდის შეფარდების ზღვარს წარგუმენტის ზრდა Δ x, როდესაც ეს უკანასკნელი თვითნებურად იხრება ნულისკენ.
გაითვალისწინეთ, რომ ერთი და იგივე ფუნქციისთვის წარმოებული სხვადასხვა წერტილში xშეუძლია მიიღოს სხვადასხვა ღირებულებები, ე.ი. წარმოებული შეიძლება ჩაითვალოს არგუმენტის ფუნქციად x. ეს ფუნქცია დანიშნულია ვ "(x)
წარმოებული აღინიშნება სიმბოლოებით ვ "(x), y", . წარმოებულის სპეციფიკური მნიშვნელობა ზე x = aაღინიშნება ვ "(ა) ან წ "| x=a.
ფუნქციის წარმოებულის პოვნის ოპერაცია f(x)ეწოდება ამ ფუნქციის დიფერენციაცია.
წარმოებულის განმარტებით პირდაპირ მოსაძებნად, შეგიძლიათ გამოიყენოთ შემდეგი: ემპირიული წესი:
მაგალითები.
წარმოებულის მექანიკური გრძნობა
ფიზიკიდან ცნობილია, რომ ერთგვაროვანი მოძრაობის კანონს აქვს ფორმა s = v t, სად ს– გზამ გაიარა დროის მომენტამდე ტ, ვ- ერთიანი მოძრაობის სიჩქარე.
თუმცა იმის გამო ბუნებაში მოძრაობების უმეტესობა არათანაბარია, შემდეგ ზოგადად სიჩქარე და, შესაბამისად, მანძილი სდროზე იქნება დამოკიდებული ტ, ე.ი. დროის ფუნქცია იქნება.
ასე რომ, მატერიალური წერტილი კანონის მიხედვით ერთი მიმართულებით მოძრაობდეს სწორი ხაზით s=s(t).
მოდით აღვნიშნოთ დროის გარკვეული მომენტი ტ 0 . ამ დროს პუნქტმა გზა გაიარა s=s(t 0 ). მოდით განვსაზღვროთ სიჩქარე ვმატერიალური წერტილი დროის მომენტში ტ 0 .
ამისათვის მოდით განვიხილოთ დროის სხვა მომენტი ტ 0 + Δ ტ. იგი შეესაბამება გავლილ გზას s =s(t 0 + Δ ტ). შემდეგ გარკვეული პერიოდის განმავლობაში Δ ტწერტილმა გაიარა Δs გზა =s(t 0 + Δ უ)–s(t).
განვიხილოთ დამოკიდებულება. მას ეწოდება საშუალო სიჩქარე Δ დროის ინტერვალში ტ. საშუალო სიჩქარე ზუსტად ვერ ახასიათებს წერტილის მოძრაობის სიჩქარეს მომენტში ტ 0 (რადგან მოძრაობა არათანაბარია). ამ ჭეშმარიტი სიჩქარის უფრო ზუსტად გამოხატვის მიზნით გამოყენებით საშუალო სიჩქარე, თქვენ უნდა გაატაროთ უფრო მოკლე დრო Δ ტ.
ასე რომ, მოძრაობის სიჩქარე შიგნით ამ მომენტშიდრო ტ 0 (მყისიერი სიჩქარე) არის საშუალო სიჩქარის ზღვარი დან ტ 0-მდე ტ 0 +Δ ტ, როდესაც Δ ტ→0:
,
იმათ. არათანაბარი სიჩქარეეს არის გავლილი მანძილის წარმოებული დროის მიმართ.
წარმოებულის გეომეტრიული მნიშვნელობა
ჯერ შემოვიღოთ მრუდის ტანგენტის განმარტება მოცემულ წერტილში.
მოდით გვქონდეს მრუდი და ფიქსირებული წერტილი მასზე M 0(იხილეთ სურათი). მეს მრუდი და დახაზეთ სეკანტი M 0 M. თუ წერტილი მიწყებს მოძრაობას მრუდის გასწვრივ და წერტილი M 0რჩება უმოძრაოდ, შემდეგ სეკანტი იცვლის თავის პოზიციას. თუ წერტილის შეუზღუდავი მიახლოებით მმრუდის გასწვრივ წერტილამდე M 0ნებისმიერ მხარეს სეკანტი მიდრეკილია დაიკავოს გარკვეული სწორი ხაზის პოზიცია M 0 T, შემდეგ პირდაპირ M 0 Tმოუწოდა მრუდის ტანგენტს მოცემულ წერტილში M 0.
რომ., ტანგენსიმრუდამდე მოცემულ წერტილში M 0სეკანტის ზღვრულ პოზიციას უწოდებენ M 0 Mროდესაც წერტილი მმიდრეკილია მრუდის გასწვრივ წერტილამდე M 0.
ახლა განვიხილოთ უწყვეტი ფუნქცია y=f(x)და ამ ფუნქციის შესაბამისი მრუდი. რაღაც ღირებულებით X 0 ფუნქცია იღებს მნიშვნელობას y 0 =f(x 0).ეს ღირებულებები x 0 და წმრუდეზე 0 შეესაბამება წერტილს M 0 (x 0 ; y 0).მოვიყვანოთ არგუმენტი x 0ნამატი Δ X. არგუმენტის ახალი მნიშვნელობა შეესაბამება ფუნქციის გაზრდილ მნიშვნელობას წ 0 +Δ y=f(x 0 –Δ x). ჩვენ ვიგებთ აზრს M(x 0+Δ x; y 0+Δ y).დავხატოთ სეკანტი M 0 Mდა ფ-ით აღვნიშნოთ ღერძის დადებითი მიმართულების სეკანტის მიერ წარმოქმნილი კუთხე ოქსი. შევქმნათ ურთიერთობა და შევამჩნიოთ, რომ .
თუ ახლა Δ x→0, მაშინ Δ ფუნქციის უწყვეტობის გამო ზე→0 და, შესაბამისად, წერტილი მ, რომელიც მოძრაობს მრუდის გასწვრივ, უახლოვდება წერტილს შეუზღუდავად M 0. შემდეგ სეკანტი M 0 Mმიდრეკილია დაიკავოს მრუდის ტანგენტის პოზიცია წერტილში M 0და კუთხე φ→α Δ-ზე x→0, სადაც α აღნიშნავს კუთხეს ღერძის ტანგენტსა და დადებით მიმართულებას შორის ოქსი. ვინაიდან tan φ ფუნქცია განუწყვეტლივ დამოკიდებულია φ-ზე φ≠π/2, შემდეგ φ→α tan φ → tan α და, შესაბამისად, ტანგენტის დახრილობა იქნება:
იმათ. f" (x)= tg α .
ამრიგად, გეომეტრიულად y" (x 0)წარმოადგენს ამ ფუნქციის გრაფიკის ტანგენტის დახრილობას წერტილში x 0, ე.ი. მოცემული არგუმენტის მნიშვნელობისთვის x, წარმოებული უდრის ფუნქციის გრაფიკზე ტანგენტის მიერ წარმოქმნილი კუთხის ტანგენტს f(x)შესაბამის წერტილში M 0 (x; y)დადებითი ღერძის მიმართულებით ოქსი.
მაგალითი.იპოვეთ მრუდის ტანგენსის დახრილობა y = x 2 წერტილში მ(-1; 1).
ჩვენ უკვე ვნახეთ, რომ ( x 2)" = 2X. მაგრამ მრუდის ტანგენსის კუთხური კოეფიციენტი არის tan α = წ"| x=-1 = – 2.
ფუნქციების განსხვავებულობა. დიფერენციალური ფუნქციის უწყვეტობა
ფუნქცია y=f(x)დაურეკა დიფერენცირებადირაღაც მომენტში x 0 თუ მას აქვს გარკვეული წარმოებული ამ ეტაპზე, ე.ი. თუ ურთიერთობის ზღვარი არსებობს და სასრულია.
თუ ფუნქცია დიფერენცირებადია გარკვეული სეგმენტის თითოეულ წერტილში [ ა; ბ] ან ინტერვალი ( ა; ბ), შემდეგ ამბობენ, რომ ის დიფერენცირებადისეგმენტზე [ ა; ბ] ან, შესაბამისად, ინტერვალში ( ა; ბ).
მოქმედებს შემდეგი თეორემა, რომელიც ადგენს კავშირს დიფერენცირებად და უწყვეტ ფუნქციებს შორის.
თეორემა.თუ ფუნქცია y=f(x)რაღაც მომენტში დიფერენცირებადი x 0, მაშინ ის ამ ეტაპზე უწყვეტია.
ამრიგად, ფუნქციის დიფერენციალურობიდან გამომდინარეობს მისი უწყვეტობა.
მტკიცებულება. თუ 
, ეს
,
სადაც α არის უსასრულო სიდიდე, ე.ი. სიდიდე, რომელიც მიდრეკილია ნულისკენ, როგორც Δ x→0. Მაგრამ შემდეგ
Δ წ=ვ "(x 0) Δ x+αΔ x=> Δ წ→0 Δ-ზე x→0, ე.ი. f(x) – f(x 0)→0 საათზე x→x 0, რაც ნიშნავს, რომ ფუნქცია f(x)უწყვეტი წერტილში x 0 . ქ.ე.დ.
ამრიგად, ფუნქციას არ შეიძლება ჰქონდეს წარმოებული უწყვეტობის წერტილებში. საპირისპირო არ არის მართალი: არის უწყვეტი ფუნქციები, რომლებიც არ არის დიფერენცირებადი ზოგიერთ წერტილში (ანუ არ აქვთ წარმოებული ამ წერტილებში).
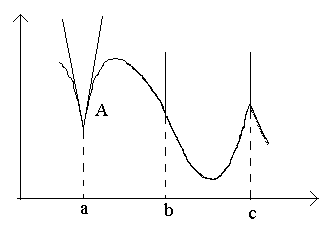
განვიხილოთ ფიგურაში მოცემული პუნქტები ა, ბ, გ.
წერტილში აΔ x→0 შეფარდებას არ აქვს ლიმიტი (რადგან ცალმხრივი ლიმიტები განსხვავებულია Δ-სთვის x→0–0 და Δ x→0+0). წერტილში აგრაფიკი არ არის განსაზღვრული ტანგენსი, მაგრამ არსებობს ორი განსხვავებული ცალმხრივი ტანგენსი დახრილებით რომ 1 და რომ 2. ამ ტიპის წერტილს კუთხის წერტილი ეწოდება.
წერტილში ბΔ x→0 თანაფარდობა არის მუდმივი ნიშანი უსასრულოდ დიდი რაოდენობით. ფუნქციას აქვს უსასრულო წარმოებული. ამ დროს გრაფიკს აქვს ვერტიკალური ტანგენსი. წერტილის ტიპი – ვერტიკალური ტანგენსის „შებრუნების წერტილი“.
წერტილში გცალმხრივი წარმოებულები არის უსასრულოდ დიდი რაოდენობით სხვადასხვა ნიშნები. ამ ეტაპზე გრაფიკს აქვს ორი შერწყმული ვერტიკალური ტანგენსი. ტიპი - "დაბრუნების წერტილი" ვერტიკალური ტანგენტით - კუთხის წერტილის განსაკუთრებული შემთხვევა.
ფუნქციის უწყვეტობა სეგმენტზე.
წერტილში ფუნქციის უწყვეტობასთან ერთად განიხილება მისი უწყვეტობა სხვადასხვა ინტერვალებით.
ფუნქციას f (x) ეწოდება უწყვეტი (a, b) ინტერვალზე, თუ ის უწყვეტია ამ ინტერვალის ყველა წერტილში.
ფუნქცია f (x) არის უწყვეტი [a, b] ინტერვალზე, თუ ის უწყვეტია (a, b) ინტერვალზე, მარჯვნივ უწყვეტი a წერტილში და მარცხენა უწყვეტი b წერტილში.
ფუნქციას ეძახიან უწყვეტი სეგმენტზე, თუ ის უწყვეტია ინტერვალში, უწყვეტი მარჯვნივ წერტილში, ანუ და უწყვეტი მარცხნივ წერტილშიეს არის .
კომენტარი.ფუნქცია, რომელიც უწყვეტია სეგმენტზე [a, b] შეიძლება იყოს წყვეტილი a და b წერტილებში (ნახ. 1).
[a, b] ინტერვალზე უწყვეტი ფუნქციების სიმრავლე აღინიშნება სიმბოლოთ C[a, b].
ძირითადი თეორემები უწყვეტი ფუნქციების შესახებ ინტერვალზე.
თეორემა 1(უწყვეტი ფუნქციის ზღვარზე). თუ ფუნქცია f (x) უწყვეტია [a, b] ინტერვალზე, მაშინ იგი შემოსაზღვრულია ამ ინტერვალზე, ე.ი. არის რიცხვი C > 0 ისეთი, რომ "x O [a, b] მოქმედებს უტოლობა | f (x)| ≤ C.
თეორემა 2(ვაიერშტრასე). თუ ფუნქცია f (x) უწყვეტია [a, b] ინტერვალზე, მაშინ ის აღწევს თავის უდიდეს მნიშვნელობას M და უმცირეს მნიშვნელობას m ამ ინტერვალზე, ე.ი. არის წერტილები α, β O [a, b] ისეთი, რომ m = f (α) ≤ f (x) ≤ f (β) = M ყველა x O [a, b] (ნახ. 2).
M-ის უდიდესი მნიშვნელობა აღინიშნება max x სიმბოლოთი O [a, b] f (x) და m-ის უმცირესი მნიშვნელობა არის სიმბოლო min x O [a, b] f(x).
თეორემა 3(ნულის არსებობის შესახებ). თუ ფუნქცია f (x) უწყვეტია [a, b] ინტერვალზე და იღებს სხვადასხვა ნიშნების არანულოვან მნიშვნელობებს სეგმენტის ბოლოებში, მაშინ ინტერვალზე (a, b) არის მინიმუმ ერთი წერტილი. ξ, სადაც f (ξ) = 0.
თეორემის გეომეტრიული მნიშვნელობა არის ის, რომ ფუნქციის გრაფიკი, რომელიც აკმაყოფილებს თეორემის პირობებს, აუცილებლად გადაკვეთს ღერძს. ოქსი(ნახ. 3).
| f(x) = 0, | (1) |
თეორემა 4(ბოლცანო–კოში). თუ ფუნქცია f (x) უწყვეტია [a, b] ინტერვალზე, მაშინ ის იღებს (a, b) ყველა შუალედურ მნიშვნელობას f (a) და f (b) შორის.
უწყვეტი ინვერსიული ფუნქციის არსებობა
ფუნქცია y = f (x) იყოს განსაზღვრული, მკაცრად ერთფეროვანი და უწყვეტი [a, b] ინტერვალზე. შემდეგ ინტერვალზე [α, β] (α = f (a), β = f (b)) არსებობს შებრუნებული ფუნქცია x = g (y), რომელიც ასევე მკაცრად ერთფეროვანი და უწყვეტია ინტერვალზე (α, β). ).
განმარტება3
.
3
მოდით იყოს რაიმე ფუნქცია, მისი განმარტების დომენი და რაღაც (ღია) ინტერვალი (შესაძლოა და/ან) 7
. დავუძახოთ ფუნქცია უწყვეტი ინტერვალზე, თუ უწყვეტი ნებისმიერ წერტილში, ანუ ნებისმიერი არსებობს 
(შემოკლებით:
მოდით ახლა იყოს (დახურული) სეგმენტი . დავუძახოთ ფუნქცია უწყვეტი სეგმენტზე, თუ უწყვეტი ინტერვალზე, უწყვეტი მარჯვნივ წერტილში და უწყვეტი მარცხნივ წერტილში, ე.ი 
მაგალითი3
.
13
განიხილეთ ფუნქცია 
(Heaviside ფუნქცია) სეგმენტზე , . შემდეგ ის უწყვეტია სეგმენტზე (მიუხედავად იმისა, რომ ამ წერტილში მას აქვს პირველი სახის შეწყვეტა).
ნახ. 3.15 ჰევისაიდის ფუნქციის გრაფიკი
მსგავსი განმარტება შეიძლება მიენიჭოს ფორმის ნახევარ ინტერვალებს და , მათ შორის შემთხვევებს და . თუმცა, ჩვენ შეგვიძლია განვაზოგადოთ ეს განმარტება თვითნებური ქვესიმრავლის შემთხვევაში შემდეგნაირად. ჯერ გავაცნობთ კონცეფციას გამოწვეულიფუძემდე: მოდით იყოს ფუძე, რომლის ყველა დაბოლოებას აქვს არა ცარიელი კვეთები . მოდით აღვნიშნოთ და განვიხილოთ ყველა სიმრავლე. ამის შემდეგ ადვილია კომპლექტის შემოწმება 
იქნება საფუძველი. ამრიგად, , და , სადაც , და არის წერტილის არაპუნქციური ორმხრივი (მარცხნივ, მარჯვნივ, შესაბამისად) უბნების ფუძეები (იხილეთ მათი განმარტება მიმდინარე თავის დასაწყისში).
განმარტება3
.
4
დავუძახოთ ფუნქცია უწყვეტი გადასაღებ მოედანზე, თუ 
ადვილი მისახვედრია, რომ მაშინ და ამ განსაზღვრებაში ემთხვევა ზემოთ მოცემულს სპეციალურად ინტერვალისა და სეგმენტისთვის.
შეგახსენებთ, რომ ყველა ელემენტარული ფუნქცია უწყვეტია მათი განსაზღვრის სფეროების ყველა წერტილში და, შესაბამისად, უწყვეტია ნებისმიერ ინტერვალებსა და სეგმენტებზე, რომლებიც დევს მათ განსაზღვრების დომენებში.
ვინაიდან უწყვეტობა ინტერვალსა და სეგმენტზე არის განსაზღვრული წერტილით, თეორემა ძალაშია, რაც თეორემა 3.1-ის უშუალო შედეგია:
თეორემა3
.
5
დაე
და
-- ფუნქციები და
-- ინტერვალი ან სეგმენტი დევს
. დაე
და
უწყვეტი ამისთვის
. შემდეგ ფუნქციები 
,
,
უწყვეტი ამისთვის
. თუ დამატებით
ყველას თვალწინ
, შემდეგ ფუნქცია
ასევე უწყვეტია
.
შემდეგი განცხადება გამომდინარეობს ამ თეორემიდან, ისევე როგორც თეორემიდან 3.1 - წინადადება 3.3:
შეთავაზება3 . 4 Რამოდენიმე ყველა ფუნქცია უწყვეტია ინტერვალზე ან სეგმენტზე -- ეს არის წრფივი სივრცე:
უწყვეტი ფუნქციის უფრო რთული თვისება გამოიხატება შემდეგი თეორემით.
თეორემა3 . 6 (უწყვეტი ფუნქციის ფესვის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე , და და -- სხვადასხვა ნიშნების რაოდენობა. (დაზუსტებისთვის, ჩვენ ვივარაუდებთ, რომ , ა .) მაშინ არის მინიმუმ ერთი ასეთი მნიშვნელობა , Რა (ანუ არის ერთი ფესვი მაინც განტოლებები ).
მტკიცებულება. მოდით შევხედოთ სეგმენტის შუაში. მაშინ ეს ან, ან, ან. პირველ შემთხვევაში აღმოჩენილია ფესვი: ეს არის . დანარჩენ ორ შემთხვევაში განიხილეთ სეგმენტის ის ნაწილი, რომლის ბოლოებზეც ფუნქცია იღებს სხვადასხვა ნიშნის მნიშვნელობებს: შემთხვევაში ან შემთხვევაში. სეგმენტის არჩეულ ნახევარს აღვნიშნავთ და იგივე პროცედურას მივმართავთ: გავყოთ ორ ნაწილად და , სადაც , და ვიპოვოთ. ფესვის აღმოჩენის შემთხვევაში; იმ შემთხვევაში, თუ ჩვენ შემდგომ განვიხილავთ სეგმენტს 
, შემთხვევაში - სეგმენტი 
და ა.შ.
ნახ. 3.16 სეგმენტის ზედიზედ გაყოფა შუაზე
ჩვენ ვიღებთ, რომ ან რომელიმე ეტაპზე აღმოჩნდება ფესვი, ან აშენდება წყობილი სეგმენტების სისტემა
რომელშიც ყოველი მომდევნო სეგმენტი წინას ნახევრად გრძელია. თანმიმდევრობა არ არის კლებადი და შემოსაზღვრულია ზემოდან (მაგალითად, რიცხვით); ამიტომ (თეორემა 2.13) მას აქვს ზღვარი. ქვემიმდევრობა 
- არამზარდი და ქვემოდან შემოსაზღვრული (მაგალითად, რიცხვით); ეს ნიშნავს, რომ არსებობს ზღვარი. ვინაიდან სეგმენტების სიგრძეები ქმნიან კლებად გეომეტრიულ პროგრესიას (მნიშვნელით), ისინი მიდრეკილნი არიან 0-მდე და 
, ანუ . მოდი ახლა დავაყენოთ. მაშინ
და 
რადგან ფუნქცია უწყვეტია. თუმცა, და , და , მიმდევრობების აგებით ისე, რომ უტოლობაში ზღვარზე გადასვლის თეორემით (თეორემა 2.7), 
და, ანუ და. ეს ნიშნავს, რომ და არის განტოლების ფესვი.
მაგალითი3
.
14
განიხილეთ ფუნქცია 
სეგმენტზე. ვინაიდან და არის სხვადასხვა ნიშნის რიცხვი, ფუნქცია 0-ზე გადადის ინტერვალის რაღაც მომენტში. ეს ნიშნავს, რომ განტოლებას აქვს ფესვი.
ნახ. 3.17 განტოლების ფესვის გრაფიკული გამოსახულება
დადასტურებული თეორემა რეალურად გვაძლევს საშუალებას ვიპოვოთ ფესვი, ყოველ შემთხვევაში, მიახლოებითი, წინასწარ განსაზღვრული სიზუსტის ნებისმიერი ხარისხით. ეს არის სეგმენტის ნახევრად გაყოფის მეთოდი, რომელიც აღწერილია თეორემის მტკიცებულებაში. ფესვის დაახლოებით პოვნის ამ და სხვა, უფრო ეფექტურ მეთოდებს უფრო დეტალურად გავეცნობით ქვემოთ, მას შემდეგ რაც შევისწავლით წარმოებულის ცნებას და თვისებებს.
გაითვალისწინეთ, რომ თეორემა არ ამბობს, რომ თუ მისი პირობები დაკმაყოფილებულია, მაშინ ფესვი უნიკალურია. როგორც ქვემოთ მოყვანილი სურათიდან ჩანს, შეიძლება იყოს ერთზე მეტი ფესვი (სურათზე არის 3).
ნახ. 3.18 ფუნქციის რამდენიმე ფესვი, რომელიც იღებს სხვადასხვა ნიშნის მნიშვნელობებს სეგმენტის ბოლოებში
ამასთან, თუ ფუნქცია მონოტონურად იზრდება ან მონოტონურად მცირდება სეგმენტზე, რომლის ბოლოებში იგი იღებს სხვადასხვა ნიშნის მნიშვნელობებს, მაშინ ფესვი უნიკალურია, რადგან მკაცრად ერთფეროვანი ფუნქცია იღებს მის თითოეულ მნიშვნელობას ზუსტად ერთ წერტილში. , მნიშვნელობის 0 ჩათვლით.
ნახ. 3.19 ერთფეროვან ფუნქციას არ შეიძლება ჰქონდეს ერთზე მეტი ფესვი
უწყვეტი ფუნქციის ფესვზე თეორემის უშუალო შედეგია შემდეგი თეორემა, რომელიც თავისთავად ძალიან მნიშვნელოვანია მათემატიკური ანალიზში.
თეორემა3 . 7 (უწყვეტი ფუნქციის შუალედური მნიშვნელობის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე და (დაზუსტებისთვის ჩვენ ვივარაუდებთ, რომ ). დაე -- რაღაც რიცხვი დევს შორის და . მაშინ არის ასეთი წერტილი , Რა .
ნახ. 3.20 უწყვეტი ფუნქცია იღებს ნებისმიერ შუალედურ მნიშვნელობას
მტკიცებულება. განვიხილოთ დამხმარე ფუნქცია 
, სად 
. მაშინ 
და 
. ფუნქცია აშკარად უწყვეტია და წინა თეორემით არის ისეთი წერტილი, რომ . მაგრამ ეს თანასწორობა ნიშნავს იმას.
გაითვალისწინეთ, რომ თუ ფუნქცია არ არის უწყვეტი, მაშინ მან შეიძლება არ მიიღოს ყველა შუალედური მნიშვნელობა. მაგალითად, Heaviside ფუნქცია (იხ. მაგალითი 3.13) იღებს მნიშვნელობებს, მაგრამ არსად, მათ შორის ინტერვალში, არ იღებს, ვთქვათ, შუალედურ მნიშვნელობას. ფაქტია, რომ Heaviside ფუნქციას აქვს შეწყვეტა ზუსტად ინტერვალში მდებარე წერტილში.
ინტერვალზე უწყვეტი ფუნქციების თვისებების შემდგომი შესასწავლად დაგვჭირდება ნამდვილ რიცხვთა სისტემის შემდეგი დახვეწილი თვისება (ეს უკვე აღვნიშნეთ მე-2 თავში მონოტონურად მზარდი შეზღუდული ფუნქციის ლიმიტის თეორემასთან დაკავშირებით): ქვემოთ შემოსაზღვრული ნებისმიერი სიმრავლე (ანუ ისეთი, რომ ყველასთვის და ზოგიერთი რიცხვისთვის იწოდება ქვედა ზღვარიკომპლექტები) ხელმისაწვდომია ზუსტი ქვედა ზღვარი, ანუ ყველაზე დიდი რიცხვებიდან ისეთი რომ ყველასთვის . ანალოგიურად, თუ ნაკრები ზემოთ არის შემოსაზღვრული, მაშინ მას აქვს ზუსტი ზედა ზღვარი: ეს არის ყველაზე პატარა ზედა სახეები(რისთვისაც ყველასთვის).
ნახ. 3.21 შემოსაზღვრული ნაკრების ქვედა და ზედა საზღვრები
თუ , მაშინ არის წერტილების არ მზარდი თანმიმდევრობა, რომელიც მიდრეკილია . ანალოგიურად, თუ , მაშინ არის წერტილების შეუმცირებელი თანმიმდევრობა, რომელიც მიდრეკილია .
თუ წერტილი ეკუთვნის სიმრავლეს, მაშინ ეს არის ამ სიმრავლის უმცირესი ელემენტი: ; ანალოგიურად თუ 
, რომ .
გარდა ამისა, შემდგომისთვის დაგვჭირდება შემდეგი
ლემა3 . 1 დაე -- უწყვეტი ფუნქცია სეგმენტზე და ბევრი იმ წერტილებს , რომელშიც (ან , ან ) არ არის ცარიელი. მერე უხვად არის უმცირესი ღირებულება , ისეთივე როგორც ყველას თვალწინ .
ნახ. 3.22 ყველაზე პატარა არგუმენტი, რომლის დროსაც ფუნქცია იღებს მითითებულ მნიშვნელობას
მტკიცებულება. ვინაიდან ეს არის შემოსაზღვრული ნაკრები (ის არის სეგმენტის ნაწილი), მას აქვს infimum. მაშინ არსებობს არამზარდი თანმიმდევრობა , , ისეთი რომ . უფრო მეტიც, კომპლექტის განმარტებით. ამიტომ, ზღვარზე გადასვლისას, ჩვენ ვიღებთ, ერთი მხრივ,
და მეორე მხრივ, ფუნქციის უწყვეტობის გამო,
ეს ნიშნავს , ასე რომ წერტილი ეკუთვნის სიმრავლეს და .
იმ შემთხვევაში, როდესაც სიმრავლე განისაზღვრება უტოლობით, ჩვენ გვაქვს ყველასთვის და უტოლობაში ზღვრამდე გადასვლის თეორემა გვაქვს.
საიდან , რაც იმას ნიშნავს რომ და . ანალოგიურად, უთანასწორობის შემთხვევაში, უტოლობაში ზღვარზე გადასვლა იძლევა
საიდან და .
თეორემა3 . 8 (უწყვეტი ფუნქციის შეზღუდვის შესახებ) დაუშვით ფუნქცია უწყვეტი სეგმენტზე . მაშინ შეზღუდული , ანუ არის ასეთი მუდმივი , Რა ყველას თვალწინ .
ნახ. 3.23 სეგმენტზე უწყვეტი ფუნქცია შემოსაზღვრულია
მტკიცებულება. დავუშვათ საპირისპირო: არ იყოს შეზღუდული, მაგალითად, ზემოდან. მაშინ ყველა კომპლექტი , , , არ არის ცარიელი. წინა ლემის მიხედვით, თითოეულ ამ კომპლექტს აქვს ყველაზე მცირე მნიშვნელობა, . ეს ვაჩვენოთ
მართლა, 
. თუ რომელიმე წერტილი, მაგალითად, არის და შორის, მაშინ
ანუ შუალედური მნიშვნელობა და . ეს ნიშნავს, რომ უწყვეტი ფუნქციის შუალედური მნიშვნელობის თეორემით, არსებობს ისეთი წერტილი, რომ 
, და . მაგრამ, იმის საპირისპიროდ, რომ - სიმრავლის უმცირესი მნიშვნელობა. აქედან გამომდინარეობს, რომ ყველასთვის.
ანალოგიურად, შემდგომში დამტკიცებულია, რომ ყველასთვის, ყველასთვის და ა.შ. ასე რომ, მზარდი თანმიმდევრობა შემოსაზღვრულია ზემოთ რიცხვით. ამიტომ ის არსებობს. ფუნქციის უწყვეტობიდან გამომდინარეობს, რომ არსებობს 
, მაგრამ 
ზე, ასე რომ არ არის ლიმიტი. შედეგად მიღებული წინააღმდეგობა ადასტურებს, რომ ფუნქცია შემოსაზღვრულია ზემოთ.
ანალოგიურად დასტურდება, რომ იგი შემოსაზღვრულია ქვემოდან, რაც გულისხმობს თეორემის დებულებას.
ცხადია, შეუძლებელია თეორემის პირობების შესუსტება: თუ ფუნქცია არ არის უწყვეტი, მაშინ ის არ უნდა იყოს შემოსაზღვრული ინტერვალზე (მაგალითად ვაძლევთ ფუნქციას
სეგმენტზე. ეს ფუნქცია არ არის შემოსაზღვრული ინტერვალით, რადგან at აქვს მეორე სახის შეწყვეტის წერტილი, ისეთი, რომ 
ზე. ასევე შეუძლებელია თეორემის მდგომარეობაში სეგმენტის ინტერვალით ან ნახევარინტერვალით ჩანაცვლება: მაგალითად, განიხილეთ იგივე ფუნქცია ნახევარ ინტერვალზე. ფუნქცია უწყვეტია ამ ნახევარ ინტერვალზე, მაგრამ შეუზღუდავია, იმის გამო, რომ .
საუკეთესო მუდმივების პოვნა, რომლებიც შეიძლება გამოყენებულ იქნას ფუნქციის ზემოდან და ქვემოდან მოცემულ ინტერვალზე შესაზღუდად, ბუნებრივად მიგვიყვანს ამ ინტერვალზე უწყვეტი ფუნქციის მინიმალური და მაქსიმუმის პოვნის პრობლემამდე. ამ პრობლემის გადაჭრის შესაძლებლობა აღწერილია შემდეგი თეორემით.
თეორემა3
.
9
(უკიდურობის მიღწევის შესახებ უწყვეტი ფუნქციით) დაუშვით ფუნქცია
უწყვეტი სეგმენტზე
. მაშინ არის წერტილი
, ისეთივე როგორც
ყველას თვალწინ
(ანუ
-- მინიმალური ქულა: 
), და არის წერტილი
, ისეთივე როგორც 
ყველას თვალწინ
(ანუ
-- მაქსიმალური ქულა: 
). სხვა სიტყვებით რომ ვთქვათ, მინიმალური და მაქსიმალური 8
სეგმენტზე უწყვეტი ფუნქციის მნიშვნელობები არსებობს და მიიღწევა ზოგიერთ წერტილში
და
ამ სეგმენტს.
ნახ. 3.24 სეგმენტზე უწყვეტი ფუნქცია აღწევს მაქსიმუმს და მინიმუმს
მტკიცებულება. ვინაიდან, წინა თეორემის მიხედვით, ფუნქცია შემოსაზღვრულია ზემოდან, ფუნქციის მნიშვნელობებისთვის არის ზუსტი ზედა ზღვარი -- რიცხვით. 
. ამრიგად, სიმრავლეები ,..., ,..., არ არის ცარიელი და წინა ლემის მიხედვით ისინი შეიცავს უმცირეს მნიშვნელობებს: 
, . ისინი არ მცირდება (ეს განცხადება დადასტურებულია ზუსტად ისევე, როგორც წინა თეორემაში):
და შემოიფარგლება ზემოდან . მაშასადამე, მონოტონური შემოსაზღვრული მიმდევრობის ზღვრის შესახებ თეორემით არსებობს ზღვარი Since 
, მაშინ
უთანასწორობაში ზღვარზე გადასვლის თეორემით, ანუ . მაგრამ ყველასთან, მათ შორის. აქედან გამოდის, რომ, ანუ ფუნქციის მაქსიმუმი მიიღწევა წერტილში.
ანალოგიურად დასტურდება მინიმალური ქულის არსებობა.
ამ თეორემაში, ისევე როგორც წინაში, შეუძლებელია პირობების შესუსტება: თუ ფუნქცია არ არის უწყვეტი, მაშინ მან შეიძლება ვერ მიაღწიოს თავის მაქსიმალურ ან მინიმალურ მნიშვნელობას სეგმენტზე, თუნდაც ის შეზღუდული იყოს. მაგალითად, ავიღოთ ფუნქცია
სეგმენტზე. ეს ფუნქცია შემოსაზღვრულია ინტერვალზე (ცხადია) და 
, თუმცა, ის არ იღებს მნიშვნელობას 1 სეგმენტის არცერთ წერტილში (გაითვალისწინეთ, რომ და არა 1). ფაქტია, რომ ამ ფუნქციას აქვს პირველი ტიპის უწყვეტობა წერტილში , ასე რომ ლიმიტი არ არის 0 წერტილის ფუნქციის მნიშვნელობის ტოლი. გარდა ამისა, უწყვეტი ფუნქცია განსაზღვრულია ინტერვალზე ან სხვა სიმრავლეზე, რომელიც არ არის დახურულ სეგმენტს (ნახევარ ინტერვალზე, ნახევრად ღერძზე) ასევე არ შეუძლია მიიღოს უკიდურესი მნიშვნელობები. მაგალითად, განიხილეთ ფუნქცია ინტერვალზე. აშკარაა, რომ ფუნქცია უწყვეტია და, თუმცა, ფუნქცია არ იღებს არც მნიშვნელობას 0 და არც მნიშვნელობას 1 ინტერვალის ნებისმიერ წერტილში. განვიხილოთ ფუნქციაც 
ღერძის ლილვზე. ეს ფუნქცია უწყვეტია, იზრდება, იღებს მის მინიმალურ მნიშვნელობას 0 წერტილში, მაგრამ არ იღებს მაქსიმალურ მნიშვნელობას ნებისმიერ წერტილში (თუმცა ზემოდან შემოიფარგლება რიცხვით და 
უწყვეტობა ელემენტარული ფუნქციები
ფუნქციების უწყვეტობის შესახებ თეორემები პირდაპირ გამომდინარეობს ლიმიტების შესახებ შესაბამისი თეორემებიდან.
თეორემა.ორი უწყვეტი ფუნქციის ჯამი, პროდუქტი და კოეფიციენტი არის უწყვეტი ფუნქცია (რაოდენობისთვის, გარდა არგუმენტის იმ მნიშვნელობებისა, რომლებშიც გამყოფი არის ნული).
თეორემა.დაუშვით ფუნქციები u= φ (x) წერტილში უწყვეტია X 0 და ფუნქცია წ = ვ(u) წერტილში უწყვეტია u 0 = φ (X 0). შემდეგ კომპლექსური ფუნქცია ვ(φ (x)) უწყვეტი ფუნქციებისგან შემდგარი, წერტილში უწყვეტია x 0 .
თეორემა.თუ ფუნქცია ზე = ვ(X) არის უწყვეტი და მკაცრად ერთფეროვანი [ ა; ბ] ცულები ოჰ, შემდეგ შებრუნებული ფუნქცია ზე = φ (X) ასევე უწყვეტი და მონოტონურია შესაბამის სეგმენტზე [ გ;დ] ცულები OU(მტკიცებულება არ არის).
ფუნქციებს, რომლებიც უწყვეტია ინტერვალში, აქვთ რამდენიმე მნიშვნელოვანი თვისება. მოდით ჩამოვაყალიბოთ ისინი თეორემების სახით მტკიცებულებების გარეშე.
თეორემა (ვეიერშტრასი). თუ ფუნქცია უწყვეტია სეგმენტზე, მაშინ ის აღწევს მაქსიმალურ და მინიმალურ მნიშვნელობებს ამ სეგმენტზე.
ფუნქცია ნაჩვენებია სურათზე 5 ზე = ვ(x) არის უწყვეტი ინტერვალზე [ ა; ბ], იღებს მის მაქსიმალურ მნიშვნელობას მწერტილში x 1 და ყველაზე პატარა მ-წერტილში X 2. Ვინმესთვის X [ა; ბ] უთანასწორობა მოქმედებს მ ≤ ვ(x) ≤ მ.
შედეგი.თუ ფუნქცია უწყვეტია ინტერვალზე, მაშინ ის შემოიფარგლება ამ ინტერვალზე.
თეორემა (ბოლზანო - კოში).თუ ფუნქცია ზე= ვ(x) არის უწყვეტი ინტერვალზე [ ა; ბ] და იღებს არათანაბარ მნიშვნელობებს მის ბოლოებში ვ(ა) = ადა ვ(ბ) = =IN, შემდეგ ამ სეგმენტზე იღებს ყველა შუალედურ მნიშვნელობას შორის ადა IN.
გეომეტრიულად თეორემა აშკარაა (იხ. სურ. 6).
ნებისმიერი ნომრისთვის თანშორის დადებული ადა IN, არის აზრი თანამ სეგმენტის შიგნით ისეთი რომ ვ(თან) = თან. პირდაპირ ზე = თანკვეთს ფუნქციის გრაფიკს ერთ წერტილში მაინც.
შედეგი.თუ ფუნქცია ზე = ვ(x) არის უწყვეტი ინტერვალზე [ ა; ბ] და მის ბოლოებში იღებს სხვადასხვა ნიშნის მნიშვნელობებს, შემდეგ სეგმენტის შიგნით [ ა; ბ] არის ერთი წერტილი მაინც თან, რომელშიც ეს ფუნქცია ვ(x) მიდის ნულზე: ვ(თან) = 0.
თეორემის გეომეტრიული მნიშვნელობა: თუ უწყვეტი ფუნქციის გრაფიკი გადის ღერძის ერთი მხრიდან ოჰმეორეს, შემდეგ ის კვეთს ღერძს ოქსი(იხ. სურ. 7).
ბრინჯი. 7.
განმარტება. თუ ფუნქცია ვ(x) განისაზღვრება ინტერვალზე [ ა, ბ], არის უწყვეტი ინტერვალის თითოეულ წერტილში ( ა, ბ), წერტილში აუწყვეტი მარჯვნივ, წერტილში ბარის უწყვეტი მარცხნივ, მაშინ ვამბობთ, რომ ფუნქცია ვ(x) უწყვეტი სეგმენტზე [ა, ბ].
სხვა სიტყვებით რომ ვთქვათ, ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], თუ დაკმაყოფილებულია სამი პირობა:
1) "x 0 Î( ა, ბ): ვ(x) = ვ(x 0);
2) ვ(x) = ვ(ა);
3) ვ(x) = ვ(ბ).
ფუნქციებისთვის, რომლებიც უწყვეტია ინტერვალზე, განვიხილავთ ზოგიერთ თვისებას, რომელსაც ვაყალიბებთ შემდეგი თეორემების სახით, მტკიცებულებების განხორციელების გარეშე.
თეორემა 1. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], შემდეგ ის აღწევს თავის მინიმალურ და მაქსიმალურ მნიშვნელობებს ამ სეგმენტზე.
ეს თეორემა აცხადებს (ნახ. 1.15), რომ სეგმენტზე [ ა, ბ] არის ასეთი წერტილი x 1 რომ ვ(x 1) £ ვ(x) ნებისმიერისთვის xდან [ ა, ბ] და რომ არსებობს წერტილი x 2 (x 2 О[ ა, ბ]) ისეთივე როგორც " xÎ[ ა, ბ] (ვ(x 2)³ ვ(x)).
მნიშვნელობა ვ(x 1) არის უდიდესი მოცემული ფუნქციისთვის [ ა, ბ], ა ვ(x 2) – ყველაზე პატარა. აღვნიშნოთ: ვ(x 1) = მ, ვ(x 2) =მ. ვინაიდან ამისთვის ვ(x) უტოლობა მოქმედებს: " xÎ[ ა, ბ] მ£ ვ(x) £ მ, შემდეგ მივიღებთ შემდეგ დასკვნას თეორემა 1-დან.
შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე, შემდეგ ის შემოიფარგლება ამ ინტერვალზე.
თეორემა 2. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] და იღებს სხვადასხვა ნიშნის მნიშვნელობებს სეგმენტის ბოლოებში, მაშინ არის ასეთი შიდა წერტილი x 0 სეგმენტი [ ა, ბ], რომელშიც ფუნქცია გადადის 0-ზე, ე.ი. $ x 0 Î ( ა, ბ) (ვ(x 0) = 0).
ეს თეორემა ამბობს, რომ ფუნქციის გრაფიკი y = ვ(x), უწყვეტი ინტერვალზე [ ა, ბ], კვეთს ღერძს ოქსიერთხელ მაინც თუ ღირებულებები ვ(ა) და ვ(ბ) აქვს საპირისპირო ნიშნები. ასე რომ, (ნახ. 1.16) ვ(ა) > 0, ვ(ბ) < 0 и функция ვ(x) წერტილებში ხდება 0 x 1 , x 2 , x 3 .
თეორემა 3. დაუშვით ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], ვ(ა) = ა, ვ(ბ) = ბდა ა¹ ბ. (სურ. 1.17). შემდეგ ნებისმიერი ნომრისთვის C, ჩასმულია ნომრებს შორის ადა ბ, არის ასეთი შინაგანი წერტილი x 0 სეგმენტი [ ა, ბ], Რა ვ(x 0) = C.
შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], მ- უმცირესი ღირებულება ვ(x), მ- ფუნქციის უდიდესი მნიშვნელობა ვ(x) სეგმენტზე [ ა, ბ], მაშინ ფუნქცია იღებს (ერთხელ მაინც) ნებისმიერ მნიშვნელობას მშორის დადებული მდა მდა, შესაბამისად, სეგმენტი [ მ, მ] არის ყველა ფუნქციის მნიშვნელობების ნაკრები ვ(x) სეგმენტზე [ ა, ბ].
გაითვალისწინეთ, რომ თუ ფუნქცია უწყვეტია ინტერვალზე ( ა, ბ) ან აქვს სეგმენტზე [ ა, ბ] შეწყვეტის წერტილები, შემდეგ თეორემები 1, 2, 3 ასეთი ფუნქციისთვის წყვეტს ჭეშმარიტებას.
დასასრულს, განიხილეთ თეორემა შებრუნებული ფუნქციის არსებობის შესახებ.
შეგახსენებთ, რომ ინტერვალში ვგულისხმობთ სეგმენტს ან ინტერვალს, ან ნახევარ ინტერვალს, სასრულს ან უსასრულობას.
 |
თეორემა 4. დაე ვ(x) არის უწყვეტი ინტერვალზე X, იზრდება (ან მცირდება) მიერ Xდა აქვს მნიშვნელობების სპექტრი ი. შემდეგ ფუნქციისთვის y = ვ(x) არის შებრუნებული ფუნქცია x= ჯ(წ), განსაზღვრულია ინტერვალზე ი, უწყვეტი და მზარდი (ან კლებადი) მიერ იმრავალი მნიშვნელობით X.
კომენტარი. დაუშვით ფუნქცია x= ჯ(წ) არის ფუნქციის შებრუნებული ვ(x). ვინაიდან არგუმენტი ჩვეულებრივ აღინიშნება x, და ფუნქცია მეშვეობით წ, შემდეგ ვწერთ შებრუნებულ ფუნქციას ფორმაში y=ჯ(x).
მაგალითი 1. ფუნქცია y = x 2 (სურ. 1.8, ა) კომპლექტზე X= }
შეიძლება სასარგებლო იყოს წაკითხვა:
- ლუკუმა - ხილის აღწერა და მისი თვისებები კულინარიაში გამოყენება;
- რეცეპტები ფეტვი წვნიანი ისტორიული ირონია თევზის, ხორცის, მჭლე;
- რას ამბობს ცვეტკოვის ოცნების წიგნი?;
- გველისა და მაიმუნის თავსებადობა;
- ტურგენევი, მუმუს მუშაობის ანალიზი, გეგმა;
- სსრკ-ს ტერიტორიის ოკუპაცია მესამე რაიხის ჯარების მიერ ვერმახტის ჯარისკაცების ფოტოებში;
- ტორტის ყუთი ყვითელი ქრიზანთემებით;
- კორეული ბადრიჯანი - უგემრიელესი რეცეპტი;