პატარა კონუსის მოცულობა. კონუსის მოცულობა
კონუსის მოცულობის საპოვნელად საჭიროა დამატებითი კონსტრუქციების გაკეთება.
ჩვენ ვაშენებთ რეგულარულ n-გონალურ პირამიდას, რომელიც ჩაწერილია კონუსში და აღწერს რეგულარულ n-გონალურ პირამიდას ამ კონუსის გარშემო.
ჩაწერილი პირამიდა შეიცავს კონუსს. აქედან გამომდინარეობს, რომ მისი მოცულობა არ აღემატება კონუსის მოცულობას.
აღწერილი პირამიდა შეიცავს კონუსს, რაც ნიშნავს, რომ მისი მოცულობა არ არის კონუსის მოცულობაზე ნაკლები.
შემოხაზული პირამიდის ძირში ჩავწეროთ წრე.
თუ ჩაწერილი რეგულარული n-გონის რადიუსი უდრის R-ს, მაშინ მასში ჩაწერილი წრის რადიუსი ტოლი იქნება: 

ჩაწერილი პირამიდის მოცულობა გამოითვლება ფორმულით:
სადაც S არის პირამიდის საფუძველი.
ჩაწერილი პირამიდის ფუძის ფართობი არ არის მასში შემავალი წრის ფართობზე ნაკლები.
მაშასადამე, განცხადება, რომ კონუსში ჩაწერილი პირამიდის მოცულობა არის მინიმუმ  უფლება.
უფლება.
აქედან გამომდინარე, შეგვიძლია ვთქვათ, რომ ამ პირამიდის შემცველი კონუსის მოცულობა იქნება მეტი ან ტოლი 
V≥ ![]()
ახლა ჩვენ აღვწერთ წრეს კონუსის გარშემო აღწერილი პირამიდის ფუძის გარშემო.
ამ წრის რადიუსი იქნება: 
ამ წრის ფართობი გამოითვლება ფორმულით: 
აღწერილი პირამიდის ფუძე მოთავსებულია მის გარშემო შემოხაზულ წრეში. ამრიგად, პირამიდის ფუძის ფართობი არ არის მეტი
მაშასადამე, განცხადება, რომ შემოხაზული პირამიდის მოცულობა აღარ შეესაბამება სიმართლეს.
ამრიგად, შეგვიძლია ვთქვათ, რომ ამ პირამიდის შემცველი კონუსის მოცულობა იქნება ნაკლები ან ტოლი ![]()
ორი მიღებული უტოლობა ტოლია ნებისმიერი n-ისთვის. თუ მაშინ
მაშინ პირველი უტოლობიდან გამომდინარეობს, რომ V≥
მეორე უტოლობიდან ![]()
თუ მართკუთხა სამკუთხედი ბრუნავს მისი ერთ-ერთი ფეხის გარშემო, მაშინ მიიღება გეომეტრიული სხეული, რომელიც ითვლება ბრუნვის კონუსად ან სწორ წრიულ კონუსად. კონუსი შემოსაზღვრულია ძირით და გვერდითი ზედაპირით. კონუსის ძირში არის წრე, რომლის რადიუსი უდრის მეორე ფეხის მნიშვნელობას. კონუსის ზემოდან ძირამდე პერპენდიკულარულად დახატული სწორი ხაზი მისი სიმაღლეა. კონუსის მოცულობა გამოითვლება რამდენიმე ფორმულის გამოყენებით. 1 მეთოდი გულისხმობს კონუსის მოცულობის განსაზღვრას, როდესაც ცნობილია მისი ფუძის სიმაღლე და ფართობი, ფორმულის მიხედვით:
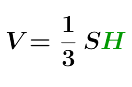
ფუძის ფართობი აღინიშნება S-ით;
კონუსის სიმაღლე H-ს გავლით.
კონუსის მოცულობა გამოითვლება როგორც კონუსის სიმაღლის ნამრავლი მისი ფუძის ფართობზე გაყოფილი 3-ზე.
Გამოყენებით ონლაინ კალკულატორიშეგიძლიათ სწრაფად და სწორად გამოთვალოთ კონუსის მოცულობა რომელიმე ზემოთ ჩამოთვლილი მეთოდით.
კონუსის მოცულობის გაანგარიშება ბაზის ფართობზე
მეორე მეთოდი გვთავაზობს კონუსის მოცულობის გამოთვლას მისი რადიუსის მნიშვნელობით ფორმულის მიხედვით:
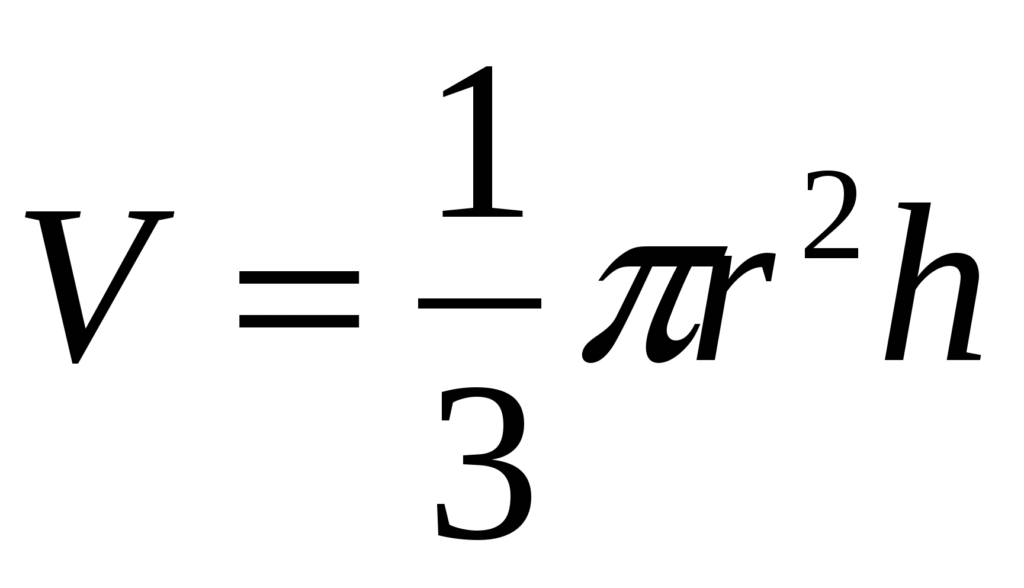
r არის კონუსის რადიუსი;
h არის სიმაღლე.
კონუსის მოცულობის მნიშვნელობა გამოითვლება, როგორც ფუძის რადიუსის კვადრატისა და სიმაღლის ნამრავლის მესამედი და პი რიცხვი, უდრის 3,1415...
მივედით კონუსებთან და ცილინდრებთან. მათ გარდა, რომლებიც უკვე გამოქვეყნებულია, იქნება დაახლოებით ცხრა სტატია, განვიხილავთ ყველა სახის დავალებას. თუ წლის განმავლობაში ღია ბანკიდაემატება ახალი ამოცანები, რა თქმა უნდა, ისინიც განთავსდება ბლოგზე. ამ სტატიაში მოცემულია რამდენიმე მაგალითი, რომლებიც დაკავშირებულია მოცულობის გაანგარიშებასთან. საკმარისი არ არის კონუსის მოცულობის ფორმულის ცოდნა, სხვათა შორის, აქ არის:

ჩვენ შეგვიძლია დავწეროთ:
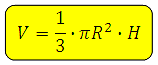
თქვენ ასევე უნდა გესმოდეთ, თუ როგორ არის დაკავშირებული მსგავსი სხეულების მოცულობა. ეს არის გაგება და არა მხოლოდ ფორმულის სწავლა. Ის აქ არის:

ანუ, თუ სხეულის წრფივ ზომებს k-ჯერ გავზრდით (ვამცირებთ), მაშინ მიღებული სხეულის მოცულობის შეფარდება ორიგინალის მოცულობასთან k 3-ის ტოლი იქნება.
ᲨᲔᲜᲘᲨᲕᲜᲐ! არ აქვს მნიშვნელობა როგორ განსაზღვრავთ ტომებს:
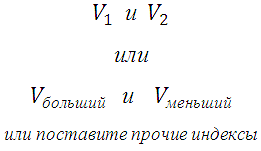
ფაქტია, რომ პრობლემების გადაჭრის პროცესში ასეთი ორგანოების განხილვისას ზოგიერთი შეიძლება აირიოს კოეფიციენტმა k. შეიძლება გაჩნდეს კითხვა - რის ტოლია?
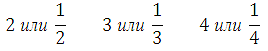
(დამოკიდებულია პირობაში მითითებულ მნიშვნელობაზე)
ეს ყველაფერი დამოკიდებულია იმაზე, თუ რომელ მხარეს უყურებთ. მნიშვნელოვანია ამის გაგება! განვიხილოთ მაგალითი - მოცემულია კუბი, მეორე კუბის კიდე სამჯერ დიდია:
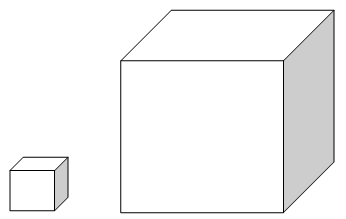
IN ამ საქმესმსგავსების კოეფიციენტი უდრის სამს (კიდე გაზრდილია სამჯერ), რაც ნიშნავს, რომ თანაფარდობა ასე გამოიყურება:
ანუ მიღებული (დიდი) კუბის მოცულობა 27-ჯერ დიდი იქნება.
შეგიძლიათ მეორე მხრიდან შეხედოთ.
კუბის გათვალისწინებით, მეორე კუბის კიდე სამჯერ მცირეა:
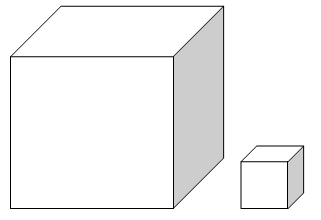
მსგავსების კოეფიციენტი უდრის მესამედს (კიდეების შემცირება სამჯერ), რაც ნიშნავს, რომ თანაფარდობა ასე გამოიყურება:
ანუ, მიღებული კუბის მოცულობა 27-ჯერ ნაკლები იქნება.
დასკვნა! ინდექსები არ არის მნიშვნელოვანი მოცულობების აღნიშვნისას, მნიშვნელოვანია გვესმოდეს, თუ როგორ განიხილება სხეულები ერთმანეთთან შედარებით.
Ნათელია, რომ:
- თუ თავდაპირველი სხეული იზრდება, მაშინ კოეფიციენტი ერთზე მეტი იქნება.
- თუ ორიგინალური სხეული მცირდება, მაშინ კოეფიციენტი ერთზე ნაკლები იქნება.
მოცულობის თანაფარდობის შესახებ შეგვიძლია ვთქვათ შემდეგი:
- თუ ამოცანაში უფრო დიდი სხეულის მოცულობას გავყოფთ პატარაზე, მაშინ მივიღებთ მსგავსების კოეფიციენტის კუბს და თავად კოეფიციენტი ერთზე მეტი აღმოჩნდება.
- თუ პატარა სხეულის მოცულობას გავყოფთ უფრო დიდზე, მივიღებთ მსგავსების კოეფიციენტის კუბს და თავად კოეფიციენტი ერთზე ნაკლები აღმოჩნდება.
ყველაზე მნიშვნელოვანი, რაც უნდა გვახსოვდეს, არის ის, რომ როდესაც საქმე ეხება მსგავსი სხეულების მოცულობას, მსგავსების კოეფიციენტს აქვს მესამე ხარისხი და არა მეორე, როგორც უბნების შემთხვევაში.
კიდევ ერთი პუნქტი რაც შეეხება.
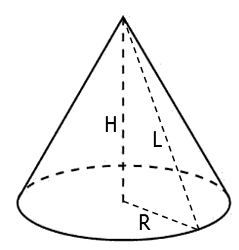
მდგომარეობა შეიცავს ისეთ რამეს, როგორიცაა კონუსის გენერაცია. ეს არის სეგმენტი, რომელიც აკავშირებს კონუსის ზედა ნაწილს ფუძის წრეწირის წერტილებთან (ნახაზზე მითითებულია ასო L-ით).
აქ აღსანიშნავია, რომ ჩვენ გავაანალიზებთ პრობლემებს მხოლოდ პირდაპირი კონუსით (შემდგომში უბრალოდ კონუსი). მარჯვენა კონუსის გენერატორები ტოლია.
განიხილეთ დავალებები:
72353. კონუსის მოცულობა არის 10. სიმაღლის შუაში გაყვანილია მონაკვეთი კონუსის ფუძის პარალელურად, რომელიც არის იგივე წვეროს მქონე პატარა კონუსის ფუძე. იპოვეთ პატარა კონუსის მოცულობა.

ჩვენ მაშინვე აღვნიშნავთ, რომ ორიგინალური და შეკვეცილი კონუსები მსგავსია და თუ გავითვალისწინებთ შეკვეცილ კონუსს ორიგინალთან შედარებით, მაშინ შეგვიძლია ვთქვათ ეს: პატარა კონუსი მსგავსია უფრო დიდის კოეფიციენტით ტოლი ერთი წამი ან 0,5. ჩვენ შეგვიძლია დავწეროთ:
შეიძლებოდა ეწერა:
შეიძლება ასე იფიქრო!
განვიხილოთ ორიგინალური კონუსი მოჭრილთან მიმართებაში. შეგვიძლია ვთქვათ, რომ უფრო დიდი კონუსი წაჭრილის მსგავსია ორი კოეფიციენტით, ვწერთ:
ახლა შეხედეთ გამოსავალს მსგავსების თვისებების გამოყენების გარეშე.
კონუსის მოცულობა უდრის მისი ფუძისა და სიმაღლის ფართობის ნამრავლის მესამედს:
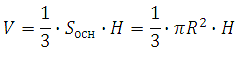
განვიხილოთ გვერდითი პროექცია (გვერდითი ხედი) მითითებული მონაკვეთით:
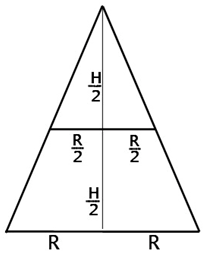
უფრო დიდი კონუსის რადიუსი იყოს R, სიმაღლე არის H. მონაკვეთი (პატარა კონუსის ფუძე) გადის სიმაღლის შუაზე, ამიტომ მისი სიმაღლე იქნება H/2-ის ტოლი. და ბაზის რადიუსი არის R/2, ეს გამომდინარეობს სამკუთხედების მსგავსებიდან.
მოდით დავწეროთ ორიგინალური კონუსის მოცულობა:
![]()
ამოჭრილი კონუსის მოცულობა ტოლი იქნება:
Ისე დეტალური გადაწყვეტილებებიწარმოდგენილია ისე, რომ თქვენ ხედავთ, თუ როგორ შეგიძლიათ შექმნათ მსჯელობა. იმოქმედეთ ნებისმიერი გზით - მთავარია, გაიგოთ გადაწყვეტილების არსი. დაე, თქვენს მიერ არჩეული გზა არ იყოს რაციონალური, შედეგი მნიშვნელოვანია (სწორი შედეგი).
პასუხი: 1.25
318145. კონუსის ფორმის ჭურჭელში სითხის დონე აღწევს სიმაღლის ნახევარს. სითხის მოცულობა 70 მლ. რამდენი მილილიტრი სითხე უნდა დაემატოს ჭურჭლის სრულად შესავსებად?
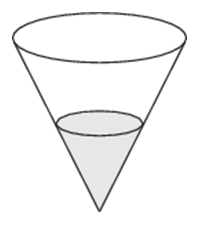
ეს დავალება წინას მსგავსია. მიუხედავად იმისა, რომ აქ სითხეზეა საუბარი, ხსნარის პრინციპი იგივეა.
ჩვენ გვაქვს ორი კონუსი - ეს არის თავად ჭურჭელი და "პატარა" კონუსი (ივსება სითხით), ისინი მსგავსია. ცნობილია, რომ მსგავსი სხეულების მოცულობა დაკავშირებულია შემდეგნაირად:
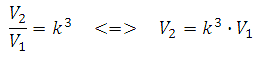
ორიგინალური კონუსი (ჭურჭელი) მსგავსია სითხით სავსე კონუსის, რომლის კოეფიციენტი უდრის 2-ს, რადგან ამბობენ, რომ სითხის დონე აღწევს სიმაღლის ნახევარს. შეგიძლიათ დაწეროთ უფრო დეტალურად:

ჩვენ ვიანგარიშებთ:
ამრიგად, თქვენ უნდა დაამატოთ:
პასუხი: 490
სხვა სითხის პრობლემები.
74257. იპოვეთ კონუსის V მოცულობა, რომლის გენერატრიქსი არის 44 და მიდრეკილია ფუძის სიბრტყეზე 30 0 კუთხით. მიეცით თქვენი პასუხი V/Pi.

კონუსის მოცულობა:
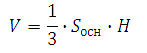
კონუსის სიმაღლეს ვპოულობთ მართკუთხა სამკუთხედის თვისებით.
30° კუთხის მოპირდაპირე ფეხი უდრის ჰიპოტენუზის ნახევარს. ჰიპოტენუზა, ამ შემთხვევაში, არის კონუსის გენერაცია. ამრიგად, კონუსის სიმაღლეა 22.
ჩვენ ვიპოვით ფუძის რადიუსის კვადრატს პითაგორას თეორემის გამოყენებით:
*ჩვენ გვჭირდება რადიუსის კვადრატი და არა თავად რადიუსი.
მაშინ მოცულობა იქნება:
სფერო, რომლის მოცულობა არის 8π, ჩაწერილია კუბში. იპოვეთ კუბის მოცულობა.
გამოსავალი
დაე იყოს კუბის მხარე. მაშინ კუბის მოცულობა არის V = a 3.
ვინაიდან ბურთი კუბშია ჩაწერილი, ბურთის რადიუსი უდრის კუბის კიდის ნახევარს, ანუ R = a/2 (იხ. ნახ.).
ბურთის მოცულობა არის V w \u003d (4/3)πR 3 და უდრის 8π, შესაბამისად
(4/3)πR 3 = 8π,
და კუბის მოცულობა არის V = a 3 = (2R) 3 = 8R 3 = 8*6 = 48.
ამოცანა B9 (შესწავლა 2015 წ.)
კონუსის მოცულობა არის 32. სიმაღლის შუაში კონუსის ფუძის პარალელურად გავლებულია მონაკვეთი, რომელიც არის იგივე წვეროს მქონე პატარა კონუსის ფუძე. იპოვეთ პატარა კონუსის მოცულობა.
გამოსავალი
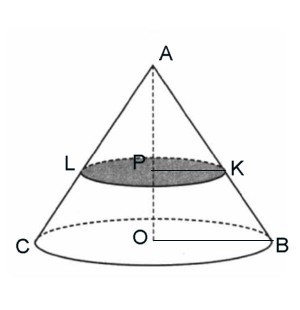
უფრო დიდი კონუსის მოცულობაა V k1 = (1/3)π(OB) 2 *AO = 32.
უფრო პატარა კონუსის მოცულობაა V k2 = (1/3)π(PK) 2 *AP =(1/3)π(1/2 OB) 2 *(1/2 AO) = (1/3)π (OB) 2 *AO*1/8 = 32/8 = 4.
ეს ნიშნავს, რომ პატარა კონუსის მოცულობა 8-ჯერ ნაკლებია და უდრის 4-ს.
ამოცანა B9 (შესწავლა 2015 წ.)
კონუსის მოცულობა არის 40. სიმაღლის შუაში კონუსის ფუძის პარალელურად გავლებულია მონაკვეთი, რომელიც არის იგივე წვეროს მქონე პატარა კონუსის ფუძე. იპოვეთ პატარა კონუსის მოცულობა.
გამოსავალი

ვინაიდან მონაკვეთი დახაზულია კონუსის სიმაღლის შუაში, მაშინ AP = 1/2 AO და PK = 1/2 OB. ანუ პატარა კონუსის სიმაღლე და რადიუსი 2-ჯერ ნაკლებია, შესაბამისად, უფრო დიდი კონუსის სიმაღლესა და რადიუსზე.
უფრო დიდი კონუსის მოცულობა უდრის V k1 \u003d (1/3) π (OB) 2 * AO \u003d 40.
უფრო პატარა კონუსის მოცულობაა V k2 = (1/3)π(PK) 2 *AP =(1/3)π(1/2 OB) 2 *(1/2 AO) = (1/3)π (OB) 2 *AO*1/8 = 40/8 = 5.
გეომეტრიულ სხეულთა მრავალფეროვნებას შორის ერთ-ერთი ყველაზე საინტერესოა კონუსი. იგი წარმოიქმნება მისი ერთ-ერთი ფეხის გარშემო მართკუთხა სამკუთხედის ბრუნვით.
როგორ მოვძებნოთ კონუსის მოცულობა - ძირითადი ცნებები
სანამ კონუსის მოცულობის გამოთვლას დაიწყებთ, უნდა გაეცნოთ ძირითად ცნებებს.
- წრიული კონუსი - ასეთი კონუსის საფუძველი არის წრე. თუ ფუძე არის ელიფსი, პარაბოლა ან ჰიპერბოლა, მაშინ ფიგურებს უწოდებენ ელიფსურ, პარაბოლურ ან ჰიპერბოლურ კონუსებს. უნდა გვახსოვდეს, რომ ბოლო ორი ტიპის გირჩს აქვს უსასრულო მოცულობა.
- შეკვეცილი კონუსი არის კონუსის ნაწილი, რომელიც მდებარეობს ფუძესა და ამ ფუძის პარალელურ სიბრტყეს შორის, რომელიც მდებარეობს ზედა და ფუძეს შორის.
- სიმაღლე - ზემოდან გამოშვებული ძირის პერპენდიკულარული სეგმენტი.
- კონუსის გენერაცია არის სეგმენტი, რომელიც აკავშირებს ფუძისა და ზედა საზღვარს.
კონუსის მოცულობა
კონუსის მოცულობის გამოსათვლელად გამოიყენება ფორმულა V=1/3*S*H, სადაც S არის ფუძის ფართობი, H არის სიმაღლე. ვინაიდან კონუსის საფუძველი არის წრე, მისი ფართობი გვხვდება ფორმულით S= nR^2, სადაც n = 3.14, R არის წრის რადიუსი.
არის სიტუაცია, როდესაც ზოგიერთი პარამეტრი უცნობია: სიმაღლე, რადიუსი ან გენერატორი. ამ შემთხვევაში, ღირს პითაგორას თეორემას მივმართოთ. კონუსის ღერძული მონაკვეთი არის ორმხრივი სამკუთხედი, რომელიც შედგება ორისაგან მართკუთხა სამკუთხედი, სადაც l არის ჰიპოტენუზა და H და R არის ფეხები. შემდეგ l=(H^2+R^2)^1/2.
შეკვეცილი კონუსის მოცულობა
დამსხვრეული კონუსი არის კონუსი მოჭრილი ზედა.
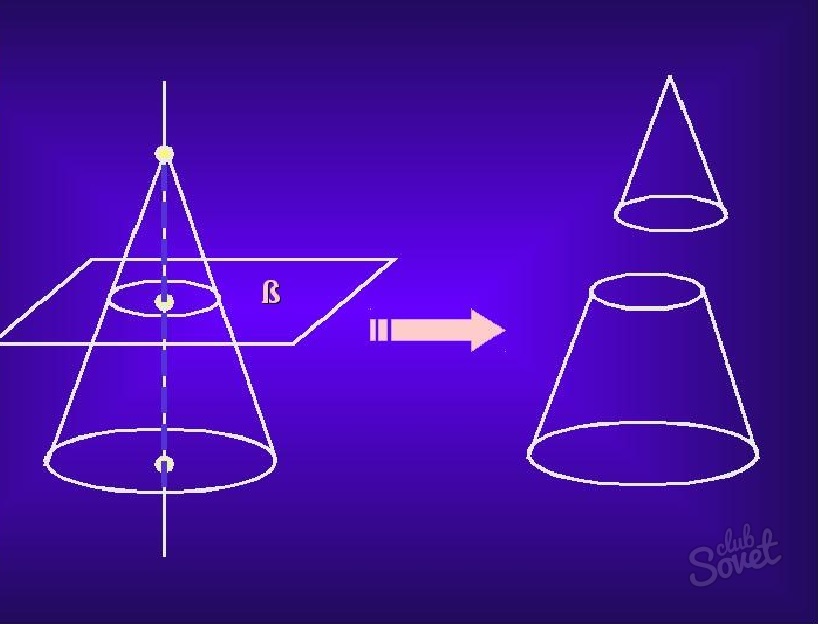
ასეთი კონუსის მოცულობის საპოვნელად საჭიროა ფორმულა:
V=1/3*n*H*(r^2+rR+R^2),
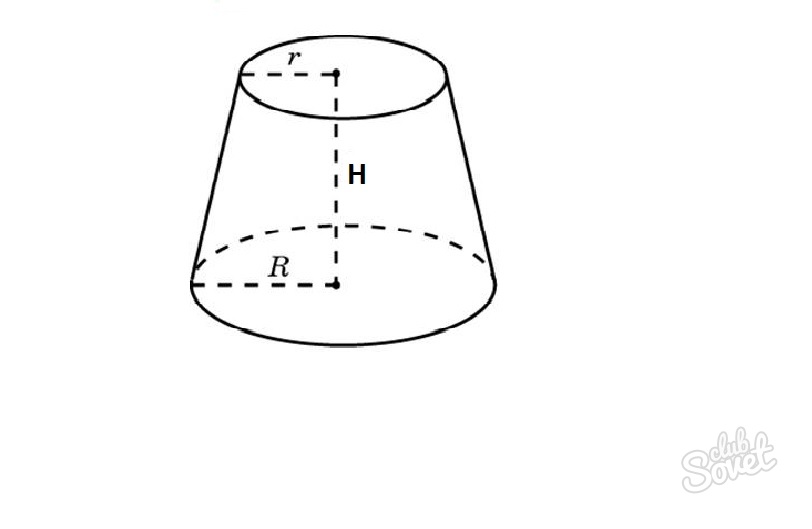
სადაც n=3.14, r არის მონაკვეთის წრის რადიუსი, R არის დიდი ფუძის რადიუსი, H არის სიმაღლე.
შეკვეცილი კონუსის ღერძული მონაკვეთი იქნება ტოლფერდა ტრაპეცია. ამიტომ, თუ საჭიროა კონუსის გენერატრიქსის სიგრძის ან ერთ-ერთი წრის რადიუსის პოვნა, ღირს ფორმულების გამოყენება ტრაპეციის გვერდებისა და ფუძეების მოსაძებნად.
იპოვეთ კონუსის მოცულობა, თუ მისი სიმაღლეა 8 სმ და ფუძის რადიუსი 3 სმ.
მოცემულია: H=8 სმ, R=3 სმ.
პირველი, იპოვეთ ბაზის ფართობი ფორმულის გამოყენებით S=nR^2.
S=3.14*3^2=28.26სმ^2
ახლა, V=1/3*S*H ფორმულის გამოყენებით ვპოულობთ კონუსის მოცულობას.
V=1/3*28.26*8=75.36სმ^3
კონუსის ფორმის ფიგურები გვხვდება ყველგან: პარკინგის კონუსები, შენობის კოშკები, სანათური. ამიტომ, იმის ცოდნა, თუ როგორ უნდა იპოვოთ კონუსის მოცულობა, ზოგჯერ შეიძლება გამოგადგეთ როგორც პროფესიულ, ისე ყოველდღიურ ცხოვრებაში.
შეიძლება სასარგებლო იყოს წაკითხვა:
- მკურნალობა საზღვარგარეთ. ნუ გეშინია. საზღვარგარეთ მკურნალობა - სამედიცინო ტურიზმის ძირითადი მიმართულებები საზღვარგარეთ მკურნალობა სად ჯობია;
- კითხვა მაქვს: როგორ მოვიშორო სტრესი;
- მთავარი ტრაგედიები Romina Power Albano Carrisi ბავშვების ცხოვრებაში რას აკეთებენ ისინი;
- რა უნდა გააკეთოს, თუ ბავშვს არ სურს საბავშვო ბაღში მეგობრობა;
- ქინძი - სასარგებლო თვისებები და გამოყენება ქინძის ეთერზეთი კოსმეტოლოგიაში;
- კლასიკური ვინეგრეტი მჟავე კომბოსტოთი - ეტაპობრივი რეცეპტი ფოტოთი;
- ჯანსაღ სხეულში ჯანსაღი გონება?;
- პენსიონერის სამსახურიდან გათავისუფლების პროცედურა: არსებული საფუძველი და შეზღუდვები და როგორ შეგიძლიათ დაიცვათ თქვენი უფლებები?;