cos თანაფარდობა. მართკუთხა სამკუთხედი. დეტალური თეორია მაგალითებით

ინსტრუქცია

მეთოდი 1. პითაგორას თეორემის გამოყენება. თეორემა ამბობს: ჰიპოტენუზის კვადრატი უდრის ფეხების კვადრატების ჯამს. აქედან გამომდინარეობს, რომ მართკუთხა სამკუთხედის ნებისმიერი გვერდი შეიძლება გამოითვალოს მისი სხვა ორი გვერდის ცოდნით (ნახ. 2).

მეთოდი 2. იქიდან გამომდინარეობს, რომ გამოყვანილი მედიანა სწორი კუთხეჰიპოტენუზამდე, ქმნის 3 მსგავს სამკუთხედს ერთმანეთთან (ნახ. 3). ამ ფიგურაში სამკუთხედები ABC, BCD და ACD მსგავსია.



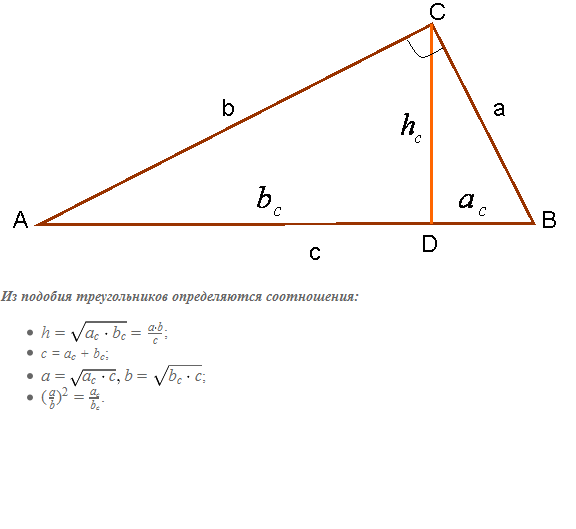
ჰიპოტენუზა არის მართკუთხა სამკუთხედის გვერდი, რომელიც მოპირდაპირეა 90 გრადუსიანი კუთხით. მისი სიგრძის გამოსათვლელად საკმარისია ვიცოდეთ ერთ-ერთი ფეხის სიგრძე და სამკუთხედის ერთ-ერთი მწვავე კუთხის მნიშვნელობა.

ინსტრუქცია

ცნობილი ფეხით და მართკუთხა სამკუთხედის მწვავე კუთხით, მაშინ ჰიპოტენუზის ზომა შეიძლება ტოლი იყოს ფეხის თანაფარდობაზე ამ კუთხის კოსინუსთან / სინუსთან, თუ ეს კუთხე არის საპირისპირო / მის გვერდით:

h = C1(ან C2)/sinα;

h = С1(ან С2)/cosα.

მაგალითი: მოცემულია ABC მართკუთხა სამკუთხედი ჰიპოტენუზით AB და მართი კუთხით C. მოდით კუთხე B იყოს 60 გრადუსი და კუთხე A 30 გრადუსი, BC ფეხის სიგრძე 8 სმ. იპოვეთ AB ჰიპოტენუზის სიგრძე. ამისათვის შეგიძლიათ გამოიყენოთ ზემოთ შემოთავაზებული ნებისმიერი მეთოდი:

AB=BC/cos60=8 სმ.

AB = BC/sin30 = 8 სმ.

ჰიპოტენუზა არის მართკუთხა სამკუთხედის გვერდი, რომელიც მართი კუთხის საპირისპიროა. ეს არის მართკუთხა სამკუთხედის ყველაზე გრძელი გვერდი. მისი გამოთვლა შეგიძლიათ პითაგორას თეორემის ან ტრიგონომეტრიული ფუნქციების ფორმულების გამოყენებით.

ინსტრუქცია

ფეხებს უწოდებენ მართკუთხა სამკუთხედის გვერდებს მართი კუთხის მიმდებარედ. ფიგურაში, ფეხები მითითებულია როგორც AB და BC. მიეცით ორივე ფეხის სიგრძე. ავღნიშნოთ ისინი როგორც |AB| და |ძვ.წ.|. ჰიპოტენუზის |AC|-ის სიგრძის საპოვნელად ვიყენებთ პითაგორას თეორემას. ამ თეორემის მიხედვით, ფეხის კვადრატების ჯამი უდრის ჰიპოტენუზის კვადრატს, ე.ი. ჩვენი ნახატის აღნიშვნაში |AB|^2 + |BC|^2 = |AC|^2. ფორმულიდან ვიღებთ, რომ ჰიპოტენუზის AC სიგრძე გვხვდება |AC| = √(|AB|^2 + |BC|^2) .

განვიხილოთ მაგალითი. მოდით, ფეხების სიგრძე |AB| = 13, |ძვ.წ.| = 21. პითაგორას თეორემით ვიღებთ, რომ |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610. 610 ნომრიდან: |AC| = √610. მთელი რიცხვების კვადრატების ცხრილის გამოყენებით აღმოვაჩენთ, რომ რიცხვი 610 არ არის რომელიმე მთელი რიცხვის სრულყოფილი კვადრატი. ჰიპოტენუზის სიგრძის საბოლოო მნიშვნელობა რომ მივიღოთ, შევეცადოთ ამოიღოთ სრული კვადრატი ფესვის ნიშნის ქვეშ. ამისათვის ჩვენ ვანაწილებთ რიცხვს 610 ფაქტორებად. 610 = 2 * 5 * 61. ცხრილის მიხედვით მარტივი რიცხვებიჩვენ ვხედავთ, რომ 61 არის მარტივი რიცხვი. ამიტომ √610 რიცხვის შემდგომი შემცირება შეუძლებელია. ვიღებთ საბოლოო პასუხს |AC| = √610.
თუ ჰიპოტენუზის კვადრატი იყო, მაგალითად, 675, მაშინ √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. თუ ასეთი ჩამოსხმა შესაძლებელია, შეასრულეთ საპირისპირო შემოწმება - შედეგის კვადრატი და შეადარე თავდაპირველ მნიშვნელობას.

გვაცნობეთ ერთ-ერთი ფეხი და მის მიმდებარე კუთხე. დაზუსტებისთვის, ეს იყოს ფეხი |AB| და კუთხე α. შემდეგ შეგვიძლია გამოვიყენოთ ტრიგონომეტრიული ფუნქციის კოსინუსის ფორმულა - კუთხის კოსინუსი უდრის მიმდებარე ფეხის შეფარდებას ჰიპოტენუზასთან. იმათ. ჩვენს აღნიშვნაში cos α = |AB| / |AC|. აქედან ვიღებთ ჰიპოტენუზის სიგრძეს |AC| = |AB| / cosα.
თუ ვიცით ფეხი |ძვ.წ.| და კუთხე α, შემდეგ ვიყენებთ კუთხის სინუსის გამოსათვლელ ფორმულას - კუთხის სინუსი უდრის მოპირდაპირე ფეხის შეფარდებას ჰიპოტენუზასთან: sin α = |BC| / |AC|. მივიღებთ, რომ ჰიპოტენუზის სიგრძე გვხვდება როგორც |AC| = |ძვ.წ.| / cosα.

სიცხადისთვის, განიხილეთ მაგალითი. მოდით ფეხის სიგრძე |AB| = 15. და კუთხე α = 60°. ვიღებთ |AC| = 15 / cos 60 ° = 15 / 0.5 = 30.
იფიქრეთ იმაზე, თუ როგორ შეგიძლიათ შეამოწმოთ თქვენი შედეგი პითაგორას თეორემის გამოყენებით. ამისათვის ჩვენ უნდა გამოვთვალოთ მეორე ფეხის სიგრძე |BC|. tg α = |BC| კუთხის ტანგენტის ფორმულის გამოყენებით / |AC|, ვიღებთ |ძვ.წ.| = |AB| * tg α = 15 * tg 60 ° = 15 * √3. შემდეგი, ჩვენ ვიყენებთ პითაგორას თეორემას, ვიღებთ 15^2 + (15 * √3)^2 = 30^2 => 225 + 675 = 900. შემოწმება დასრულებულია.

სასარგებლო რჩევა

ჰიპოტენუზის გამოთვლის შემდეგ შეამოწმეთ, აკმაყოფილებს თუ არა მიღებული მნიშვნელობა პითაგორას თეორემას.

წყაროები:

  • მარტივი რიცხვების ცხრილი 1-დან 10000-მდე

ფეხებიდაასახელეთ მართკუთხა სამკუთხედის ორი მოკლე გვერდი, რომლებიც ქმნიან მის წვეროს, რომლის მნიშვნელობა არის 90 °. ასეთ სამკუთხედში მესამე გვერდს ჰიპოტენუზა ეწოდება. სამკუთხედის ყველა ეს გვერდი და კუთხე ერთმანეთთან არის დაკავშირებული გარკვეული ურთიერთობებით, რაც საშუალებას გაძლევთ გამოთვალოთ ფეხის სიგრძე, თუ ცნობილია რამდენიმე სხვა პარამეტრი.

ინსტრუქცია

გამოიყენეთ პითაგორას თეორემა ფეხის (A) სიგრძის გამოსათვლელად, თუ იცით მართკუთხა სამკუთხედის დანარჩენი ორი გვერდის (B და C) სიგრძე. ამ თეორემაში ნათქვამია, რომ ფეხების სიგრძის ჯამი კვადრატში უდრის ჰიპოტენუზის კვადრატს. აქედან გამომდინარეობს, რომ თითოეული ფეხის სიგრძე უდრის ჰიპოტენუზისა და მეორე ფეხის სიგრძის კვადრატებს შორის სხვაობის კვადრატულ ფესვს: A=√(C²-B²).

გამოიყენეთ პირდაპირი ტრიგონომეტრიული ფუნქციის "სინუსი" განმარტება მწვავე კუთხისთვის, თუ იცით კუთხის (α) მნიშვნელობა გამოთვლილი ფეხის საპირისპიროდ და ჰიპოტენუზის სიგრძე (C). ეს განმარტება აცხადებს, რომ ამის სინუს ცნობილი კუთხეუდრის სასურველი ფეხის სიგრძის შეფარდებას ჰიპოტენუზის სიგრძესთან. ეს ნიშნავს, რომ სასურველი ფეხის სიგრძე უდრის ჰიპოტენუზის სიგრძისა და ცნობილი კუთხის სინუსის ნამრავლს: A=C∗sin(α). იგივე ცნობილი მნიშვნელობებისთვის შეგიძლიათ გამოიყენოთ კოზეკანტური ფუნქციის განმარტება და გამოთვალოთ სასურველი სიგრძე ჰიპოტენუზის სიგრძის გაყოფით ცნობილი კუთხის კოსეკანტზე A=C/cosec(α).

გამოიყენეთ პირდაპირი ტრიგონომეტრიული ფუნქციის კოსინუსის განმარტება, თუ ჰიპოტენუზის სიგრძის გარდა (C), ასევე ცნობილია მახვილი კუთხის (β) მნიშვნელობა სასურველი ფეხის მიმდებარედ. ამ კუთხის კოსინუსი განისაზღვრება, როგორც სასურველი ფეხისა და ჰიპოტენუზის სიგრძის თანაფარდობა და აქედან შეგვიძლია დავასკვნათ, რომ ფეხის სიგრძე უდრის ჰიპოტენუზის სიგრძისა და ცნობილი კოსინუსის ნამრავლს. კუთხე: A=C∗cos(β). შეგიძლიათ გამოიყენოთ სეკანტური ფუნქციის განმარტება და გამოთვალოთ სასურველი მნიშვნელობა ჰიპოტენუზის სიგრძის გაყოფით ცნობილი კუთხის A=C/sec(β) სეკანტზე.

გამოიტანეთ საჭირო ფორმულა მსგავსი განსაზღვრებიდან ტრიგონომეტრიული ფუნქციის ტანგენტის წარმოებულისთვის, თუ სასურველი ფეხის (A) მოპირდაპირე მხარეს მდებარე მწვავე კუთხის (α) მნიშვნელობის გარდა, მეორე ფეხის (B) სიგრძეა. ცნობილია. სასურველი ფეხის მოპირდაპირე კუთხის ტანგენსი არის ამ ფეხის სიგრძის თანაფარდობა მეორე ფეხის სიგრძესთან. ეს ნიშნავს, რომ სასურველი მნიშვნელობა ტოლი იქნება ცნობილი ფეხის სიგრძისა და ცნობილი კუთხის ტანგენტის ნამრავლის: A=B∗tg(α). ამ იგივე ცნობილი რაოდენობებიდან, სხვა ფორმულა შეიძლება გამოვიდეს კოტანგენტის ფუნქციის განსაზღვრის გამოყენებით. ამ შემთხვევაში ფეხის სიგრძის გამოსათვლელად საჭირო იქნება ცნობილი ფეხის სიგრძის შეფარდება ცნობილი კუთხის კოტანგენსთან: A=B/ctg(α).

Მსგავსი ვიდეოები

სიტყვა "კატეტი" რუსულად ბერძნულიდან შემოვიდა. ზუსტი თარგმანით, ეს ნიშნავს ქლიავის ხაზს, ანუ დედამიწის ზედაპირზე პერპენდიკულარულს. მათემატიკაში ფეხებს უწოდებენ გვერდებს, რომლებიც ქმნიან მართკუთხა სამკუთხედის სწორ კუთხეს. ამ კუთხის მოპირდაპირე მხარეს ჰიპოტენუზა ეწოდება. ტერმინი "ფეხი" ასევე გამოიყენება არქიტექტურასა და შედუღების ტექნოლოგიაში.



დახაზეთ მართკუთხა სამკუთხედი ACB. მონიშნეთ მისი ფეხები a და b, და დაასახელეთ მისი ჰიპოტენუზა c. მართკუთხა სამკუთხედის ყველა გვერდი და კუთხე დაკავშირებულია გარკვეული მიმართებით. ერთ-ერთი მწვავე კუთხის მოპირდაპირე ფეხის თანაფარდობას ჰიპოტენუზასთან ეწოდება ამ კუთხის სინუსი. ამ სამკუთხედში sinCAB=a/c. კოსინუსი არის თანაფარდობა მიმდებარე ფეხის ჰიპოტენუზასთან, ანუ cosCAB=b/c. ინვერსიულ მიმართებებს უწოდებენ სეკანტურ და კოსეკანტურს.

ამ კუთხის სეკანტი მიიღება ჰიპოტენუზის მიმდებარე ფეხზე გაყოფით, ანუ secCAB=c/b. გამოდის კოსინუსის ორმხრივი, ანუ შეიძლება გამოისახოს ფორმულით secCAB=1/cosSAB.
კოსეკანტი უდრის ჰიპოტენუზის საპირისპირო ფეხზე გაყოფის კოეფიციენტს და არის სინუსის ორმხრივი. მისი გამოთვლა შესაძლებელია ფორმულის გამოყენებით cosecCAB=1/sinCAB

ორივე ფეხი უკავშირდება ტანგენტსა და კოტანგენტს. IN ამ საქმესტანგენტი იქნება a გვერდის თანაფარდობა b მხარესთან, ანუ მოპირდაპირე ფეხი მეზობელთან. ეს თანაფარდობა შეიძლება გამოიხატოს ფორმულით tgCAB=a/b. შესაბამისად, შებრუნებული თანაფარდობა იქნება კოტანგენსი: ctgCAB=b/a.

ჰიპოტენუზისა და ორივე ფეხის ზომებს შორის თანაფარდობა დაადგინა ძველმა ბერძენმა მათემატიკოსმა პითაგორამ. მის სახელობის თეორემა დღესაც გამოიყენება ხალხის მიერ. ნათქვამია, რომ ჰიპოტენუზის კვადრატი უდრის ფეხების კვადრატების ჯამს, ანუ c2 \u003d a2 + b2. შესაბამისად, თითოეული ფეხი ტოლი იქნება ჰიპოტენუზისა და მეორე ფეხის კვადრატებს შორის სხვაობის კვადრატული ფესვის. ეს ფორმულა შეიძლება დაიწეროს როგორც b=√(c2-a2).

ფეხის სიგრძე ასევე შეიძლება გამოიხატოს თქვენთვის ცნობილი ურთიერთობებით. სინუსებისა და კოსინუსების თეორემების მიხედვით, ფეხი ტოლია ჰიპოტენუზისა და ერთ-ერთი ამ ფუნქციის ნამრავლის. ის ასევე შეიძლება გამოიხატოს ტანგენტის ან კოტანგენტის მიხედვით. ფეხი a შეგიძლიათ იპოვოთ, მაგალითად, ფორმულით a \u003d b * tan CAB. ზუსტად ანალოგიურად, მოცემული ტანგენტის ან კოტანგენსიდან გამომდინარე, განისაზღვრება მეორე ფეხი.

არქიტექტურაში ასევე გამოიყენება ტერმინი „ფეხი“. იგი გამოიყენება იონურ კაპიტალზე და აღნიშნავს ქლიავის ხაზს ზურგის შუაში. ანუ, ამ შემთხვევაში, ეს ტერმინი აღნიშნავს მოცემულ წრფეზე პერპენდიკულარს.

შედუღების ტექნოლოგიაში არსებობს "ფეხის ფილე შედუღების" კონცეფცია. როგორც სხვა შემთხვევებში, ეს არის უმოკლესი მანძილი. Აქ ჩვენ ვსაუბრობთშედუღებამდე ერთ ნაწილს შორის არსებული უფსკრულის შესახებ მეორე ნაწილის ზედაპირზე მდებარე ნაკერის საზღვარზე.

Მსგავსი ვიდეოები

წყაროები:

  • რა არის ფეხი და ჰიპოტენუზა

Მსგავსი ვიდეოები

შენიშვნა

მართკუთხა სამკუთხედის გვერდების გაანგარიშებისას, მისი მახასიათებლების ცოდნა შეიძლება ითამაშოს:
1) თუ მართი კუთხის ფეხი დევს 30 გრადუსიანი კუთხის საპირისპიროდ, მაშინ ის უდრის ჰიპოტენუზის ნახევარს;
2) ჰიპოტენუზა ყოველთვის გრძელია ვიდრე რომელიმე ფეხი;
3) თუ წრე შემოიფარგლება მართკუთხა სამკუთხედის გარშემო, მაშინ მისი ცენტრი უნდა მდებარეობდეს ჰიპოტენუზის შუაში.

ტრიგონომეტრია არის მათემატიკის ფილიალი, რომელიც სწავლობს ტრიგონომეტრიულ ფუნქციებს, ასევე მათ გამოყენებას პრაქტიკაში. ეს მახასიათებლები მოიცავს სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი.

სინუსი არის ტრიგონომეტრიული ფუნქცია , მოპირდაპირე ფეხის სიდიდის თანაფარდობა ჰიპოტენუზის სიდიდესთან.

სინუსი ტრიგონომეტრიაში.

როგორც ზემოთ აღვნიშნეთ, სინუსი პირდაპირ კავშირშია ტრიგონომეტრიასთან და ტრიგონომეტრიულ ფუნქციებთან. მისი ფუნქცია განისაზღვრება

  • დაეხმარეთ კუთხის გამოთვლას, იმ პირობით, რომ ცნობილია სამკუთხედის გვერდების ზომები;
  • დაეხმარება სამკუთხედის გვერდის ზომის გამოთვლაში, იმ პირობით, რომ კუთხე ცნობილია.

უნდა გვახსოვდეს, რომ სინუსის მნიშვნელობა ყოველთვის იგივე იქნება სამკუთხედის ნებისმიერი ზომისთვის, რადგან სინუსი არ არის საზომი, არამედ თანაფარდობა.

შესაბამისად, იმისათვის, რომ არ გამოვთვალოთ ეს მუდმივი მნიშვნელობა კონკრეტული პრობლემის თითოეული ამოხსნისთვის, შეიქმნა სპეციალური ტრიგონომეტრიული ცხრილები. მათში უკვე გამოთვლილი და დაფიქსირებულია სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების მნიშვნელობები. როგორც წესი, ეს ცხრილები მოცემულია ალგებრისა და გეომეტრიის სახელმძღვანელოების ფურცლებზე. მათი ნახვა ასევე შესაძლებელია ინტერნეტში.

სინუსი გეომეტრიაში.

გეომეტრია მოითხოვს ვიზუალიზაციას, ამიტომ პრაქტიკაში გასაგებად, რა არის კუთხის სინუსი, თქვენ უნდა დახაზოთ სამკუთხედი მართი კუთხით.

დავუშვათ, რომ გვერდები, რომლებიც ქმნიან მართ კუთხეს, დასახელებულია ა, გ,საპირისპირო კუთხე X.

ჩვეულებრივ, გვერდების სიგრძე მითითებულია ამოცანებში. Მოდით ვთქვათ a=3, b=4. ამ შემთხვევაში, ასპექტის თანაფარდობა გამოიყურება ¾. უფრო მეტიც, თუ გავაგრძელებთ სამკუთხედის გვერდებს მახვილი კუთხის მიმდებარედ X, მაშინ მხარეები გაიზრდება ადა ვდა ჰიპოტენუზა არის მართკუთხა სამკუთხედის მესამე გვერდი, რომელიც არ არის მართი კუთხით ფუძესთან. ახლა სამკუთხედის გვერდები შეიძლება სხვაგვარად ეწოდოს, მაგალითად: მ, ნ, კ.

ამ მოდიფიკაციით მუშაობდა ტრიგონომეტრიის კანონი: შეიცვალა სამკუთხედის გვერდების სიგრძეები, მაგრამ მათი თანაფარდობა არა.

ძველმა მეცნიერებმა შენიშნეს ის ფაქტი, რომ თუ სამკუთხედის გვერდების სიგრძეს იმდენჯერ შეცვლით, რამდენჯერაც გსურთ და კუთხის x მნიშვნელობის შენარჩუნებით, მის გვერდებს შორის თანაფარდობა კვლავ უცვლელი დარჩება. ჩვენს შემთხვევაში, გვერდების სიგრძე შეიძლება შეიცვალოს შემდეგნაირად: a / b \u003d ¾, როცა გვერდი გახანგრძლივდება ა 6 სმ-მდე და ვ- 8 სმ-მდე ვიღებთ: მ/ნ = 6/8 = 3/4.

ამ მხრივ მართკუთხა სამკუთხედში გვერდების თანაფარდობა ეწოდება:

  • x კუთხის სინუსი არის მოპირდაპირე ფეხის შეფარდება ჰიპოტენუზასთან: sinx = a/c;
  • x კუთხის კოსინუსი არის მიმდებარე ფეხის შეფარდება ჰიპოტენუზასთან: cosx = w/s;
  • x კუთხის ტანგენსი არის მოპირდაპირე ფეხის თანაფარდობა მიმდებარესთან: tgx \u003d a / b;
  • x კუთხის კოტანგენსი არის მიმდებარე ფეხის თანაფარდობა მოპირდაპირეზე: ctgx \u003d in / a.

ჩვენ ვიწყებთ ტრიგონომეტრიის შესწავლას მართკუთხა სამკუთხედით. მოდით განვსაზღვროთ რა არის სინუსი და კოსინუსი, ასევე მახვილი კუთხის ტანგენსი და კოტანგენსი. ეს არის ტრიგონომეტრიის საფუძვლები.

გავიხსენოთ რომ სწორი კუთხეარის კუთხე ტოლი. სხვა სიტყვებით რომ ვთქვათ, გაშლილი კუთხის ნახევარი.

მკვეთრი კუთხე- უფრო პატარა.

ბუნდოვანი კუთხე- უფრო დიდი. ასეთ კუთხესთან მიმართებაში „ბლატი“ შეურაცხყოფა კი არა, მათემატიკური ტერმინია :-)


დავხატოთ მართკუთხა სამკუთხედი. მართი კუთხე ჩვეულებრივ აღინიშნება. გაითვალისწინეთ, რომ კუთხის მოპირდაპირე მხარე აღინიშნება იგივე ასოთი, მხოლოდ მცირე. ასე რომ, აღინიშნება კუთხის მოპირდაპირე მხარე.

კუთხე აღინიშნება შესაბამისი ბერძნული ასოთი.

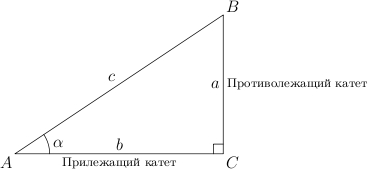
ჰიპოტენუზამართკუთხა სამკუთხედი არის მართი კუთხის მოპირდაპირე მხარე.

ფეხები- მხარეები მკვეთრი კუთხეების მოპირდაპირე მხარეს.

კუთხის მოპირდაპირე ფეხი ე.წ საწინააღმდეგო(კუთხის მიმართ). მეორე ფეხი, რომელიც კუთხის ერთ მხარეს დევს, ე.წ მიმდებარე.

სინუსიმართკუთხა სამკუთხედში მწვავე კუთხე არის მოპირდაპირე ფეხის თანაფარდობა ჰიპოტენუზასთან:

კოსინუსიმწვავე კუთხე მართკუთხა სამკუთხედში - მიმდებარე ფეხის თანაფარდობა ჰიპოტენუზასთან:

ტანგენტიმახვილი კუთხე მართკუთხა სამკუთხედში - მოპირდაპირე ფეხის თანაფარდობა მეზობელთან:

კიდევ ერთი (ექვივალენტური) განმარტება: მახვილი კუთხის ტანგენსი არის კუთხის სინუსის თანაფარდობა მის კოსინუსთან:

კოტანგენსიმახვილი კუთხე მართკუთხა სამკუთხედში - მიმდებარე ფეხის თანაფარდობა საპირისპიროსთან (ან, ექვივალენტურად, კოსინუსისა და სინუსების თანაფარდობა):

ყურადღება მიაქციეთ სინუსების, კოსინუსების, ტანგენტებისა და კოტანგენტების ძირითად თანაფარდობებს, რომლებიც მოცემულია ქვემოთ. ისინი გამოგვადგება პრობლემების გადაჭრაში.


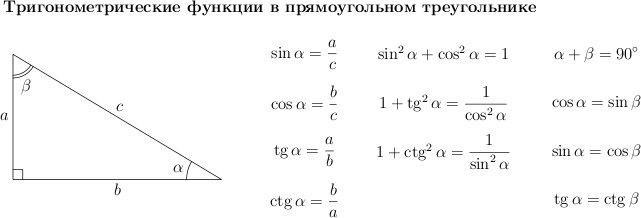
მოდით დავამტკიცოთ ზოგიერთი მათგანი.

1. ნებისმიერი სამკუთხედის კუთხეების ჯამი არის . ნიშნავს, მართკუთხა სამკუთხედის ორი მახვილი კუთხის ჯამი არის .

2. ერთის მხრივ, როგორც მოპირდაპირე ფეხის შეფარდება ჰიპოტენუზასთან. მეორეს მხრივ, რადგან კუთხისთვის ფეხი მიმდებარე იქნება.

ჩვენ ამას მივიღებთ . Სხვა სიტყვებით, .

3. აიღეთ პითაგორას თეორემა: . მოდით გავყოთ ორივე ნაწილი:

Მივიღეთ ძირითადი ტრიგონომეტრიული იდენტურობა:

ამრიგად, კუთხის სინუსის ცოდნით, შეგვიძლია ვიპოვოთ მისი კოსინუსი და პირიქით.

4. ძირითადი ტრიგონომეტრიული იდენტობის ორივე ნაწილის გაყოფით, მივიღებთ:

ეს ნიშნავს, რომ თუ ჩვენ მოგვცეს მახვილი კუთხის ტანგენსი, მაშინვე შეგვიძლია ვიპოვოთ მისი კოსინუსი.

ანალოგიურად,

კარგი, ჩვენ მივეცით განმარტებები და დაწერილი ფორმულები. მაგრამ რატომ გვჭირდება სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი?

ჩვენ ეს ვიცით ნებისმიერი სამკუთხედის კუთხეების ჯამი არის.

ჩვენ ვიცით შორის ურთიერთობა პარტიებიმართკუთხა სამკუთხედი. ეს არის პითაგორას თეორემა: .

გამოდის, რომ სამკუთხედში ორი კუთხის ცოდნით, შეგიძლიათ იპოვოთ მესამე. იცოდეთ ორი გვერდი მართკუთხა სამკუთხედში, შეგიძლიათ იპოვოთ მესამე. ასე რომ, კუთხეებისთვის - მათი თანაფარდობა, გვერდებისთვის - საკუთარი. მაგრამ რა უნდა გააკეთოს, თუ მართკუთხა სამკუთხედში ცნობილია ერთი კუთხე (გარდა მართკუთხა) და ერთი გვერდი, მაგრამ თქვენ უნდა იპოვოთ სხვა გვერდები?

თავდაპირველად, სინუსი და კოსინუსი წარმოიშვა მართკუთხა სამკუთხედებში რაოდენობების გამოთვლის აუცილებლობის გამო. შენიშნა, რომ თუ მართკუთხა სამკუთხედში კუთხეების ხარისხის საზომი მნიშვნელობა არ იცვლება, მაშინ ასპექტის თანაფარდობა, რაც არ უნდა შეიცვალოს ეს გვერდები სიგრძეში, ყოველთვის იგივე რჩება.

ასე შემოვიდა სინუსის და კოსინუსის ცნებები. მართკუთხა სამკუთხედში მწვავე კუთხის სინუსი არის მოპირდაპირე ფეხის თანაფარდობა ჰიპოტენუზასთან, ხოლო კოსინუსი არის მიმდებარე ფეხის შეფარდება ჰიპოტენუზასთან.

კოსინუსების და სინუსების თეორემები

მაგრამ კოსინუსები და სინუსები შეიძლება გამოყენებულ იქნას არა მხოლოდ მართკუთხა სამკუთხედებში. ბლაგვი ან მახვილი კუთხის, ნებისმიერი სამკუთხედის გვერდის მნიშვნელობის საპოვნელად საკმარისია კოსინუსის და სინუსების თეორემის გამოყენება.

კოსინუსების თეორემა საკმაოდ მარტივია: „სამკუთხედის გვერდის კვადრატი უდრის დანარჩენი ორი გვერდის კვადრატების ჯამის გამოკლებით ამ გვერდების ორჯერ ნამრავლს მათ შორის კუთხის კოსინუსზე“.

სინუსების თეორემის ორი ინტერპრეტაცია არსებობს: მცირე და გაფართოებული. მცირეს მიხედვით: „სამკუთხედში კუთხეები მოპირდაპირე გვერდების პროპორციულია“. ეს თეორემა ხშირად ვრცელდება სამკუთხედის გარშემო შემოხაზული წრის თვისების გამო: „სამკუთხედში კუთხეები მოპირდაპირე გვერდების პროპორციულია და მათი თანაფარდობა უდრის შემოხაზული წრის დიამეტრს“.

წარმოებულები

წარმოებული არის მათემატიკური ინსტრუმენტი, რომელიც გვიჩვენებს, თუ რამდენად სწრაფად იცვლება ფუნქცია მისი არგუმენტის ცვლილების მიმართ. წარმოებულები გამოიყენება ალგებრაში, გეომეტრიაში, ეკონომიკასა და ფიზიკაში, რიგ ტექნიკურ დისციპლინაში.

პრობლემების გადაჭრისას, თქვენ უნდა იცოდეთ ტრიგონომეტრიული ფუნქციების წარმოებულების ტაბულური მნიშვნელობები: სინუსი და კოსინუსი. სინუსის წარმოებული არის კოსინუსი, ხოლო კოსინუსის წარმოებული არის სინუსი, მაგრამ მინუს ნიშნით.

გამოყენება მათემატიკაში

განსაკუთრებით ხშირად, სინუსები და კოსინუსები გამოიყენება მართკუთხა სამკუთხედების და მათთან დაკავშირებული ამოცანების ამოხსნისას.

სინუსებისა და კოსინუსების მოხერხებულობა აისახება ტექნოლოგიაშიც. კუთხეების და გვერდების შეფასება ადვილი იყო კოსინუსებისა და სინუსების თეორემების გამოყენებით, რთული ფორმებისა და ობიექტების დაშლა "მარტივ" სამკუთხედებად. ინჟინრები და არქიტექტორები, რომლებიც ხშირად ეხებოდნენ ასპექტის თანაფარდობის და ხარისხის ზომების გამოთვლებს, დიდ დროს და ძალისხმევას უთმობდნენ არა ცხრილის კუთხეების კოსინუსების და სინუსების გამოთვლას.

შემდეგ სამაშველოში მოვიდა ბრედისის ცხრილები, რომლებიც შეიცავდა სხვადასხვა კუთხის სინუსების, კოსინუსების, ტანგენტებისა და კოტანგენტების ათასობით მნიშვნელობას. IN საბჭოთა დროზოგიერთი მასწავლებელი აიძულებდა თავის მოსწავლეებს დაემახსოვრებინათ ბრედისის ცხრილების გვერდები.

მართკუთხა სამკუთხედზე, როგორც მრავალკუთხედის უმარტივესმა, სხვადასხვა მკვლევარებმა დახვეწეს თავიანთი ცოდნა ტრიგონომეტრიის სფეროში ჯერ კიდევ იმ დღეებში, როდესაც მათემატიკის ამ სფეროს ამ სიტყვით არავინ უწოდებდა. მაშასადამე, დღეს შეუძლებელია იმ ავტორის მითითება, რომელმაც ამ ბრტყელ გეომეტრიულ ფიგურაში გამოავლინა შაბლონები გვერდების სიგრძისა და კუთხეების სიდიდეების შეფარდებაში. ასეთ ურთიერთობებს ტრიგონომეტრიულ ფუნქციებს უწოდებენ და იყოფა რამდენიმე ჯგუფად, რომელთაგან მთავარი პირობითად განიხილება "პირდაპირი" ფუნქციები. ამ ჯგუფს მხოლოდ ორი ფუნქცია აქვს მინიჭებული და მათგან ერთი არის სინუსი.

ინსტრუქცია

განმარტებით, მართკუთხა სამკუთხედში ერთ-ერთი კუთხე უდრის 90°-ს და იმის გამო, რომ მისი კუთხეების ჯამი ევკლიდეს გეომეტრიაში უნდა იყოს 180°-ის ტოლი, დანარჩენი ორი კუთხე მახვილია (ანუ 90°-ზე ნაკლები. ). ზუსტად ამ კუთხეებისა და გვერდების სიგრძის თანაფარდობების კანონზომიერებები აღწერს ტრიგონომეტრიულ ფუნქციებს.

ფუნქცია, რომელსაც ეწოდება მწვავე კუთხის სინუსი, განსაზღვრავს თანაფარდობას მართკუთხა სამკუთხედის ორი გვერდის სიგრძეებს შორის, რომელთაგან ერთი მდებარეობს ამ მახვილი კუთხის საპირისპიროდ, ხოლო მეორე მის გვერდით არის და მდებარეობს სწორი კუთხის საპირისპიროდ. ვინაიდან ასეთ სამკუთხედში მართი კუთხის მოპირდაპირე მხარეს ჰიპოტენუზა ეწოდება, დანარჩენ ორს კი ფეხი, სინუსური ფუნქციის განმარტება შეიძლება ჩამოყალიბდეს, როგორც თანაფარდობა მოპირდაპირე ფეხისა და ჰიპოტენუზას სიგრძეებს შორის.

ამ ტრიგონომეტრიული ფუნქციის ასეთი მარტივი განმარტების გარდა, დღეს უფრო რთულია: წრის მეშვეობით დეკარტის კოორდინატებში, სერიების მეშვეობით, დიფერენციალური და ფუნქციური განტოლებების ამონახსნებით. ეს ფუნქცია უწყვეტია, ანუ მისი არგუმენტები („განმარტებათა დომენი“) შეიძლება იყოს ნებისმიერი რიცხვი – უსასრულოდ უარყოფითიდან უსასრულოდ დადებითამდე. და ამ ფუნქციის მაქსიმალური და მინიმალური მნიშვნელობები შემოიფარგლება -1-დან +1-მდე დიაპაზონით - ეს არის "მისი მნიშვნელობების დიაპაზონი". სინუსი თავის მინიმალურ მნიშვნელობას იღებს 270°-ის კუთხით, რაც შეესაბამება Pi-ს 3/2-ს, ხოლო მაქსიმალური მიიღება 90°-ზე (½ Pi-ზე). ფუნქციის მნიშვნელობები ნულოვანი ხდება 0°, 180°, 360° და ა.შ. ამ ყველაფრიდან გამომდინარეობს, რომ სინუსი არის პერიოდული ფუნქცია და მისი პერიოდი უდრის 360 ° ან ორჯერ Pi რიცხვს.

მოცემული არგუმენტიდან ამ ფუნქციის მნიშვნელობების პრაქტიკული გამოთვლებისთვის შეგიძლიათ გამოიყენოთ კალკულატორი - მათი დიდი უმრავლესობა (მათ შორის ჩაშენებული პროგრამული კალკულატორი ოპერაციული სისტემათქვენი კომპიუტერი) აქვს შესაბამისი ვარიანტი.

Მსგავსი ვიდეოები

ინსტრუქცია

კუთხემართკუთხა სამკუთხედში, თქვენ უნდა გამოიყენოთ კოსინუსის განმარტება და იპოვოთ მიმდებარე ფეხის თანაფარდობა ჰიპოტენუზასთან:
cos? = a/c, სადაც a არის ფეხის სიგრძე, c არის ჰიპოტენუზის სიგრძე.

თუ კოსინუსის პოვნა გჭირდებათ კუთხეთვითნებურ სამკუთხედში აუცილებელია კოსინუსების თეორემის გამოყენება:
თუ კუთხე მწვავეა: cos? = (a2 + b2 – c2)/(2ab);
თუ კუთხე ბლაგვია: cos? = (c2 - a2 - b2)/(2ab), სადაც a, b არის კუთხის მიმდებარე გვერდების სიგრძე, c არის კუთხის მოპირდაპირე მხარის სიგრძე.

თუ კოსინუსის პოვნა გჭირდებათ კუთხეთვითნებურ გეომეტრიულ ფიგურაში აუცილებელია მნიშვნელობის დადგენა კუთხეგრადუსებში ან რადიანებში და კოსინუსი კუთხეიპოვეთ მისი სიდიდის მიხედვით საინჟინრო კალკულატორის, ბრედისის ცხრილების ან ნებისმიერი სხვა მათემატიკური პროგრამის გამოყენებით.

კოსინუსიარის კუთხის ძირითადი ტრიგონომეტრიული ფუნქცია. კოსინუსის განსაზღვრის უნარი სასარგებლოა ვექტორულ ალგებრაში ვექტორების პროგნოზების განსაზღვრისას სხვადასხვა ღერძზე.

ინსტრუქცია

cos?=(b?+c?-a?)/(2*b*c)

არის სამკუთხედი, რომლის გვერდები a, b, c ტოლია, შესაბამისად, 3, 4, 5 მმ.

იპოვე კოსინუსიდიდ გვერდებს შორის დახურული კუთხე.

მოდი ავღნიშნოთ a გვერდის მოპირდაპირე კუთხე?, შემდეგ ზემოთ მიღებული ფორმულის მიხედვით გვაქვს:

cos?=(b?+c?-a?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 =32/40=0.8

პასუხი: 0.8.

თუ სამკუთხედი მართკუთხა სამკუთხედია, მაშინ იპოვეთ კოსინუსიდა საკმარისია ვიცოდეთ კუთხის ნებისმიერი ორი მხარის სიგრძე ( კოსინუსიმარჯვენა კუთხე არის 0).

იყოს მართკუთხა სამკუთხედი a, b, c გვერდებით, სადაც c არის ჰიპოტენუზა.

განიხილეთ ყველა ვარიანტი:

იპოვეთ cos?, თუ ცნობილია a და b გვერდების სიგრძეები (სამკუთხედის ფეხები)

დამატებით გამოვიყენოთ პითაგორას თეორემა:

cos?=(ბ?+გ?-ა?)/(2*ბ*გ)=(ბ?+ბ?+ა?-ა?)/(2*ბ*ვ(ბ?+ა?)) =(2*ბ?)/(2*ბ*ვ(ბ?+ა?))=ბ/ვ(ბ?+ა?)

შედეგად მიღებული ფორმულის სისწორის შესამოწმებლად, ჩვენ ვცვლით მასში 1-ლი მაგალითის მნიშვნელობებს, ე.ი.

ელემენტარული გამოთვლების გაკეთების შემდეგ მივიღებთ:

ანალოგიურად, არსებობს კოსინუსიმართკუთხაში სამკუთხედისხვა შემთხვევებში:

ცნობილია a და c (ჰიპოტენუზა და საპირისპირო ფეხი), იპოვეთ cos?

cos?=(b?+c?-a?)/(2*b*c)=(c?-a?+c?-a?)/(2*c*v(c?-a?)) =(2*s?-2*a?)/(2*s*v(s?-a?))=v(s?-a?)/s.

პირველი მაგალითიდან a=3 და c=5 მნიშვნელობების ჩანაცვლებით მივიღებთ:

b და c ცნობილია (ჰიპოტენუზა და მიმდებარე ფეხი).

იპოვე სოსი?

მსგავსი გარდაქმნების განხორციელების შემდეგ (ნაჩვენებია მაგალითებში 2 და 3), ჩვენ ვიღებთ ამას ამ შემთხვევაში კოსინუსივ სამკუთხედიგამოითვლება ძალიან მარტივი ფორმულით:

მიღებული ფორმულის სიმარტივე ახსნილია ელემენტარული გზით: სინამდვილეში, კუთხის მიმდებარედ? ფეხი არის ჰიპოტენუზის პროექცია, ამიტომ მისი სიგრძე უდრის ჰიპოტენუზის სიგრძეს გამრავლებული cos-ზე.

პირველი მაგალითიდან b=4 და c=5 მნიშვნელობების ჩანაცვლებით მივიღებთ:

ასე რომ, ყველა ჩვენი ფორმულა სწორია.

რჩევა 5: როგორ მოვძებნოთ მახვილი კუთხე მართკუთხა სამკუთხედში

პირდაპირ ნახშირბადოვანისამკუთხედი, ალბათ, ერთ-ერთი ყველაზე ცნობილი, ისტორიული თვალსაზრისით, გეომეტრიული ფორმები. პითაგორას "შარვალს" მხოლოდ "ევრიკას!" არქიმედეს.



დაგჭირდებათ

  • - სამკუთხედის ნახაზი;
  • - მმართველი;
  • - პროტრაქტორი.

ინსტრუქცია

სამკუთხედის კუთხეების ჯამი 180 გრადუსია. მართკუთხაში სამკუთხედიერთი კუთხე (მარჯვნივ) ყოველთვის იქნება 90 გრადუსი, დანარჩენი კი მკვეთრია, ე.ი. თითოეული 90 გრადუსზე ნაკლები. მართკუთხაში რომელი კუთხის დადგენა სამკუთხედიარის სწორი, გაზომეთ სამკუთხედის გვერდები სახაზავი და დაადგინეთ ყველაზე დიდი. მას ჰიპოტენუზა (AB) ეწოდება და სწორი კუთხის (C) საპირისპიროა. დანარჩენი ორი მხარე ქმნის მართ კუთხეს და ეწოდება ფეხები (AC, BC).

მას შემდეგ რაც დაადგინეთ რომელი კუთხეა მახვილი, შეგიძლიათ გაზომოთ კუთხე პროტრაქტორით ან გამოთვალოთ ის მათემატიკური ფორმულების გამოყენებით.

პროტრატორის გამოყენებით კუთხის მნიშვნელობის დასადგენად, გაასწორეთ მისი ზედა (მოდით ავღნიშნოთ ასო A-თი) სპეციალური ნიშნით სახაზავზე პროტრატორის ცენტრში, AC ფეხი უნდა ემთხვეოდეს მის ზედა კიდეს. პროტრატორის ნახევარწრიულ ნაწილზე მონიშნეთ წერტილი, რომლითაც გადის ჰიპოტენუზა AB. მნიშვნელობა ამ ეტაპზე შეესაბამება კუთხის მნიშვნელობას გრადუსებში. თუ პროტრაქტორზე მითითებულია 2 მნიშვნელობა, მაშინ მწვავე კუთხისთვის თქვენ უნდა აირჩიოთ უფრო პატარა, ბლაგვისთვის - უფრო დიდი.

იპოვეთ მიღებული მნიშვნელობა ბრედის საცნობარო ცხრილებში და დაადგინეთ რომელი კუთხე შეესაბამება მიღებულს რიცხვითი მნიშვნელობა. ჩვენი ბებიები იყენებდნენ ამ მეთოდს.

დღესდღეობით საკმარისია აიღოთ კალკულატორი ტრიგონომეტრიული ფორმულების გამოთვლის ფუნქციით. მაგალითად, ჩაშენებული Windows კალკულატორი. გაუშვით "კალკულატორი" აპლიკაცია, მენიუს "ნახვა" პუნქტში აირჩიეთ "ინჟინერია". გამოთვალეთ სასურველი კუთხის სინუსი, მაგალითად, sin (A) = BC/AB = 2/4 = 0.5

გადართეთ კალკულატორი ინვერსიული ფუნქციის რეჟიმზე კალკულატორის ეკრანზე INV ღილაკზე დაწკაპუნებით, შემდეგ დააჭირეთ რკალის ფუნქციის გამოსათვლელ ღილაკს (მონიშნულია როგორც ცოდვა მინუს პირველ გრადუსამდე ეკრანზე). გამოთვლის ფანჯარაში გამოჩნდება შემდეგი წარწერა: asind (0.5) = 30. ანუ, სასურველი კუთხე 30 გრადუსია.

წყაროები:

  • ბრედისის ცხრილები (სინუსები, კოსინუსები)

მათემატიკაში კოსინუსების თეორემა ყველაზე ხშირად გამოიყენება, როდესაც საჭიროა მესამე მხარის პოვნა კუთხით და ორი გვერდით. თუმცა, ზოგჯერ პრობლემის მდგომარეობა საპირისპიროა: საჭიროა მოცემული სამი მხარის კუთხის პოვნა.



ინსტრუქცია

წარმოიდგინეთ, რომ გეძლევათ სამკუთხედი ორი გვერდის ცნობილი სიგრძით და ერთი კუთხის მნიშვნელობით. ამ სამკუთხედის ყველა კუთხე არ არის ერთმანეთის ტოლი და მისი გვერდებიც განსხვავებულია ზომით. კუთხე γ დევს სამკუთხედის გვერდის საპირისპიროდ, რომელიც მითითებულია როგორც AB, რომელიც არის ამ ფიგურის საფუძველი. ამ კუთხით, ისევე როგორც AC და BC დარჩენილი გვერდების მეშვეობით, შეგიძლიათ იპოვოთ სამკუთხედის ის გვერდი, რომელიც უცნობია, კოსინუსების თეორემის გამოყენებით, მის საფუძველზე ქვემოთ მოცემული ფორმულის გამომუშავება:
a^2=b^2+c^2-2bc*cosγ, სადაც a=BC, b=AB, c=AC
კოსინუსების თეორემას სხვაგვარად უწოდებენ განზოგადებულ პითაგორას თეორემას.

 

შეიძლება სასარგებლო იყოს წაკითხვა: