Vârfurile unui trapez. Material despre geometrie pe tema „trapezul și proprietățile sale”. Proprietățile unui trapez isoscel
G.I. Kovaleva
METODA DE STUDIARE A PROPRIETĂȚILOR TRAPEZIEI
În materialele diferitelor teste și examene se întâlnesc foarte des sarcini trapezoidale, a căror soluție impune elevilor să cunoască proprietățile „non-programe” ale trapezului. (Proprietățile sunt considerate a fi linia de mijloc trapez, proprietăți ale diagonalelor și unghiurilor unui trapez isoscel.) Ce proprietăți remarcabile are un trapez? Unde și când să le studiezi într-un curs de geometrie școlar?
Metodă de studiere a proprietăților unui trapez
Acum că am văzut mai multe tipuri, să învățăm despre forme care nu au proprietățile paralelogramelor. Reamintim că paralelogramele sunt patrulatere ale căror laturi opuse sunt paralele. În această secțiune, vom lua în considerare patrulatere ale căror laturi opuse se pot intersecta la un moment dat. Să începem explorarea noastră examinând unele proprietăți ale trapezelor. Definiție. Un trapez este un patrulater cu exact o pereche de laturi paralele.
După ce am studiat proprietățile liniei mediane a unui trapez, putem formula și dovedi proprietatea unui segment care leagă punctele medii ale diagonalelor unui trapez. Segmentul care leagă punctele medii ale diagonalelor unui trapez este egal cu jumătatea diferenței bazelor.
Practicând tehnica principală de rezolvare a problemelor pe trapezul „desenați două înălțimi”, elevii trebuie să ofere sarcina: „Lasă BT- înălțime trapez isoscel ABCD cu temelii î.HrȘi ANUNȚ.
 ,
,
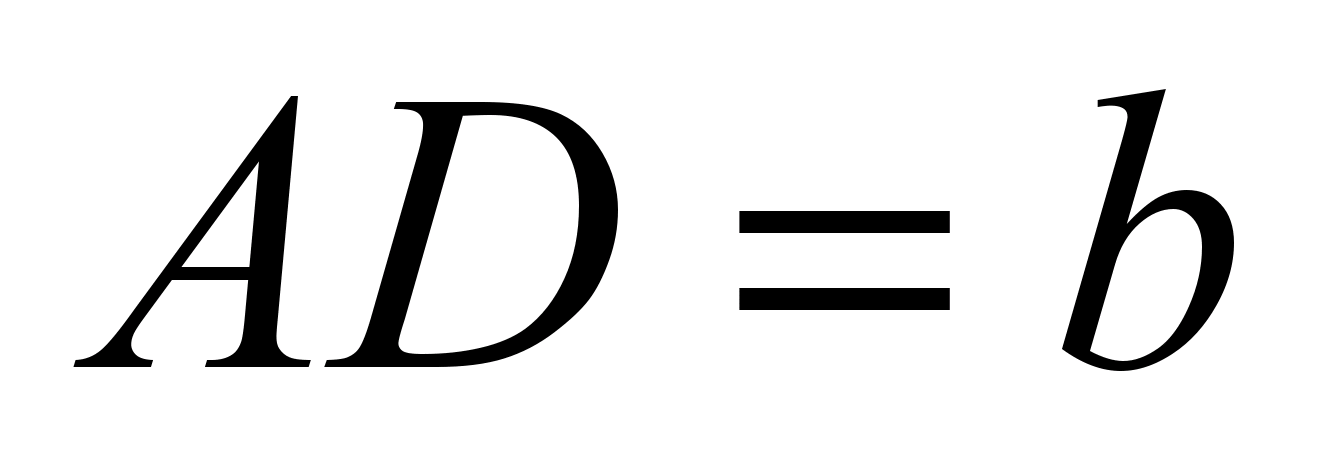 . Aflați lungimile segmentelor LAȘi TD».
. Aflați lungimile segmentelor LAȘi TD».
„Utilizarea trigonometriei în rezolvarea problemelor planimetrice”
Deoarece un trapez trebuie să aibă exact o pereche de laturi paralele, va trebui să demonstrăm că o pereche de laturi opuse este paralelă, iar cealaltă nu este în a noastră. Dacă uităm să dovedim că o pereche de laturi opuse nu este paralelă, nu excludem posibilitatea ca patrulaterul să fie paralelogram. Prin urmare, acest pas va fi absolut esențial pe măsură ce lucrăm la diferitele exerciții care implică trapezul.
Înainte de a ne scufunda direct în studiul nostru asupra trapezelor, va fi necesar să cunoaștem numele diferitelor părți ale acestor patrulatere pentru a fi specifici despre laturile și unghiurile sale. Toate trapezele conțin două părți principale: baza și picioarele. Laturile opuse ale unui trapez care sunt paralele între ele se numesc baze. Celelalte laturi ale trapezului care se intersecteaza la un moment dat daca sunt extinse se numesc picioarele trapezului.
Subiectul „Asemănarea figurilor” este foarte benefic pentru studiul proprietăților unui trapez. De exemplu, diagonalele unui trapez îl împart în patru triunghiuri, iar triunghiurile adiacente bazelor sunt similare, iar triunghiurile adiacente laturilor sunt egale. Să numim această afirmație Cuproprietatea triunghiurilor în care un trapez este împărțit cu diagonalele sale. Mai mult, prima parte a afirmației se dovedește foarte ușor prin semnul asemănării triunghiurilor în două unghiuri. A doua parte poate fi oferită studenților sub forma unei sarcini.
Asemănarea triunghiurilor trapezoidale formate
Laturile de sus și de jos ale trapezului sunt paralele una cu cealaltă, deci sunt bazele trapezului. Celelalte laturi ale trapezului se intersecteaza daca sunt extinse, deci sunt picioarele trapezului. Segmentul care leagă punctele medii ale picioarelor trapezului se numește segment de mijloc. Lungimea acestui segment este întotdeauna egală cu jumătate din suma bazelor trapezoidale sau.
Raportul dintre lungimile segmentelor și bazelor
Măsurarea segmentului mijlociu depinde numai de lungimea bazelor trapezoidale. Cu toate acestea, există caracteristică importantă că unele trapeze depind numai de picioarele ei. Să ne uităm acum la aceste trapeze. Un trapez isoscel este un trapez ale cărui picioare sunt congruente. Prin definiție, dacă un patrulater are exact o pereche de drepte paralele, atunci patrulaterul este un trapez. Definiția unui trapez isoscel adaugă o altă specificație: picioarele trapezului trebuie să fie congruente.
La fel, triunghiuri
BOCȘi AOB au o înălțime comună, dacă luăm segmente drept baze COȘi OA.
Apoi 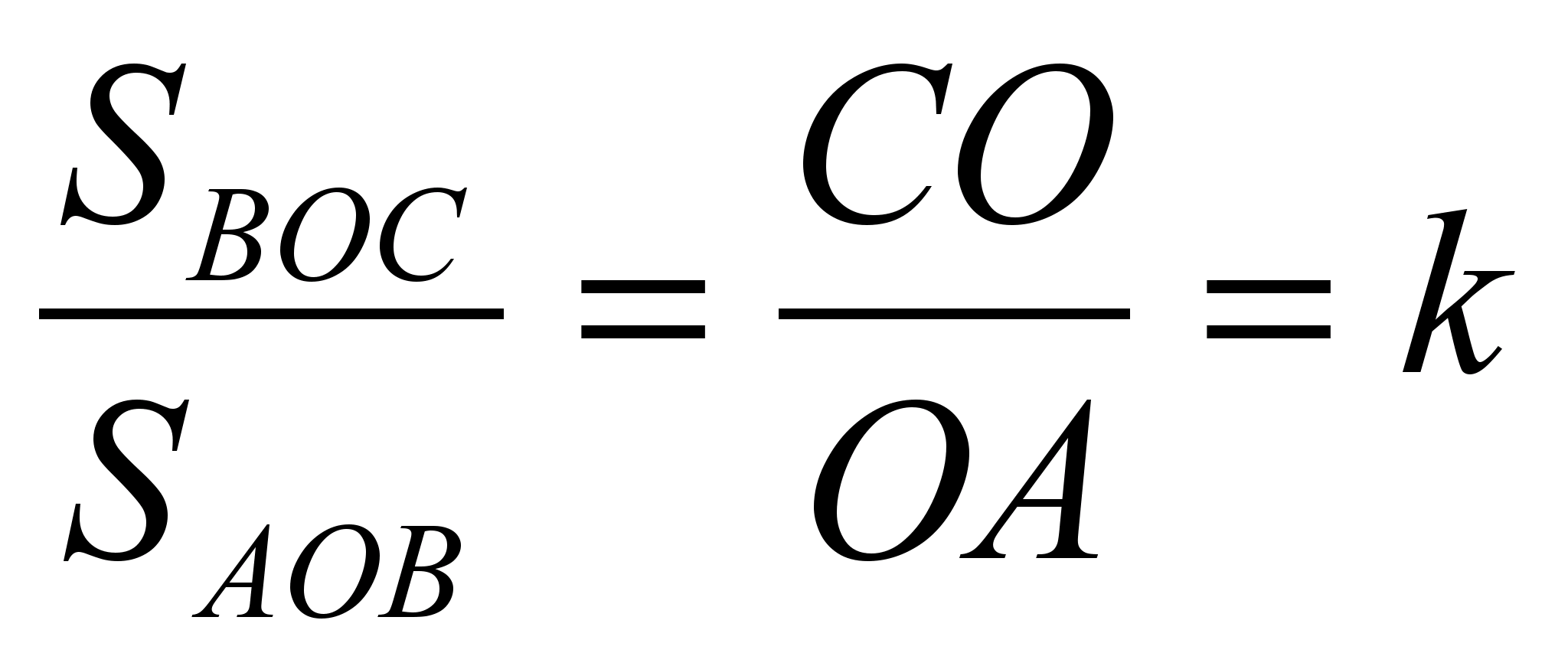 Și
Și 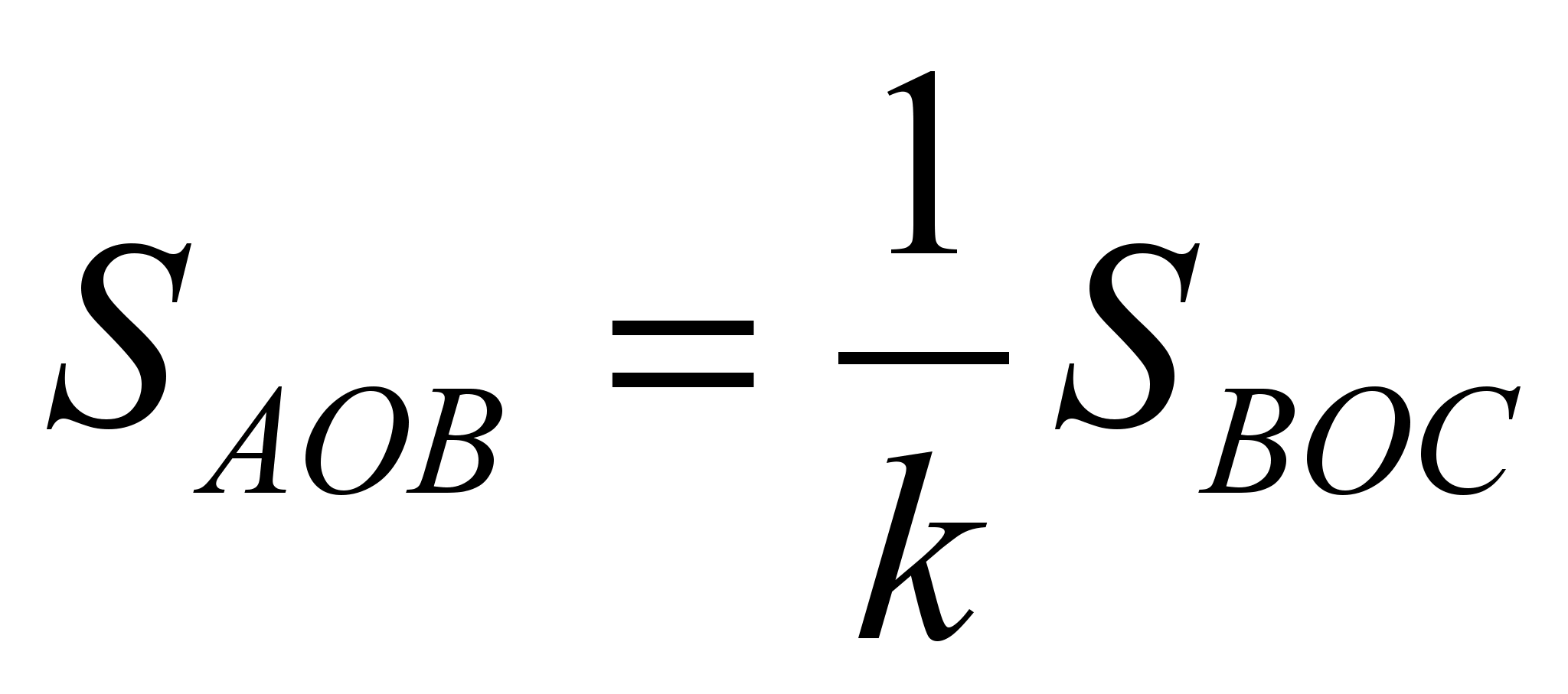 .
.
Din aceste două propoziţii rezultă că 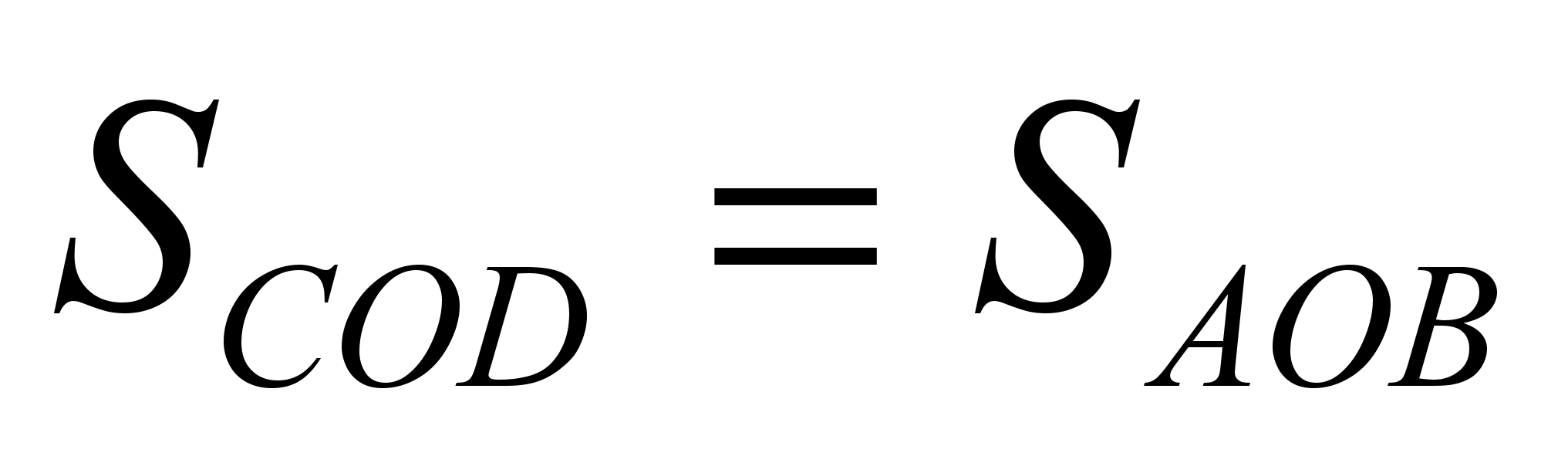 .
.
Există mai multe teoreme pe care le putem folosi pentru a ne ajuta să demonstrăm că un trapez este isoscel. Aceste proprietăți sunt enumerate mai jos. Un trapez este isoscel dacă și numai dacă unghiurile de bază sunt congruente. Un trapez este isoscel dacă și numai dacă diagonalele sunt congruente.
Dacă un trapez este isoscel, atunci unghiurile sale opuse sunt complementare. Un zmeu este un patrulater cu două perechi diferite de laturi adiacente care sunt congruente. Amintiți-vă că paralelogramele aveau și perechi de laturi congruente. Cu toate acestea, laturile lor congruente au fost întotdeauna opuse. Zmeii au două perechi de laturi congruente care se întâlnesc în două puncte diferite. Să ne uităm la ilustrația de mai jos pentru a ne ajuta să înțelegem cum arată un zmeu.
Ar fi grozav să nu ne oprim asupra afirmației formulate, ci să găsim relația dintre ariile triunghiurilor în care un trapez este împărțit cu diagonalele sale
, invitând elevii să rezolve problema: „Fie O punctul de intersecție al diagonalelor trapezului ABCD cu temelii î.HrȘi ANUNȚ. Se știe că ariile triunghiurilor BOCȘi AOD egal, respectiv  Și
Și 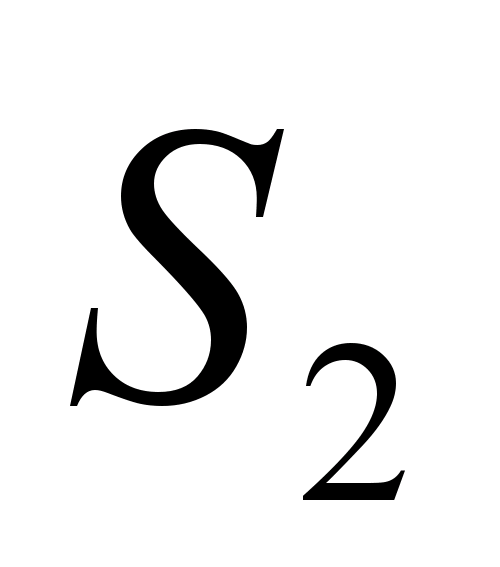 . Găsiți aria trapezului.
. Găsiți aria trapezului.
Zmeii au mai multe proprietăți care ne vor ajuta să le identificăm din alte quad-uri. Diagonalele zmeului se întâlnesc în unghi drept. Zmeii au exact o pereche de unghiuri opuse care sunt congruente. Aceste două proprietăți sunt ilustrate în diagrama de mai jos.
Aceasta este singura noastră pereche de unghiuri congruente, pentru că? Lăsați practica să facă unele dintre problemele care necesită utilizarea proprietăților trapezelor și zmeelor despre care tocmai am învățat. Deoarece ni se oferă lungimile bazelor trapezului, ne putem da seama care ar trebui să fie lungimea segmentului din mijloc. Să folosim formula pe care am dat-o pentru segmentul din mijloc pentru a înțelege acest lucru.
Deoarece . Prin urmare, din asemănarea triunghiurilor BDESPRECȘi AOD urmează că 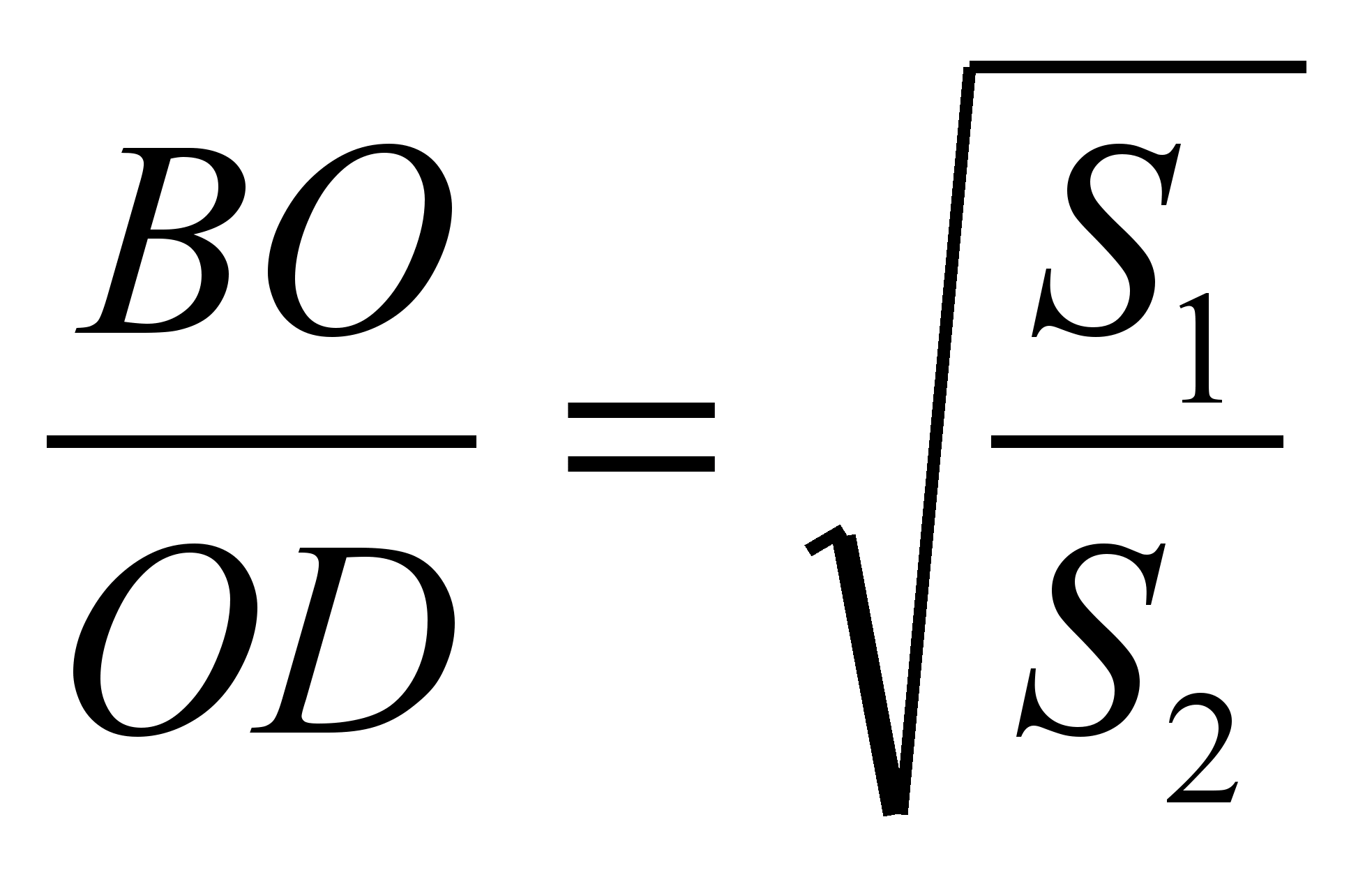 .Deci,
.Deci, 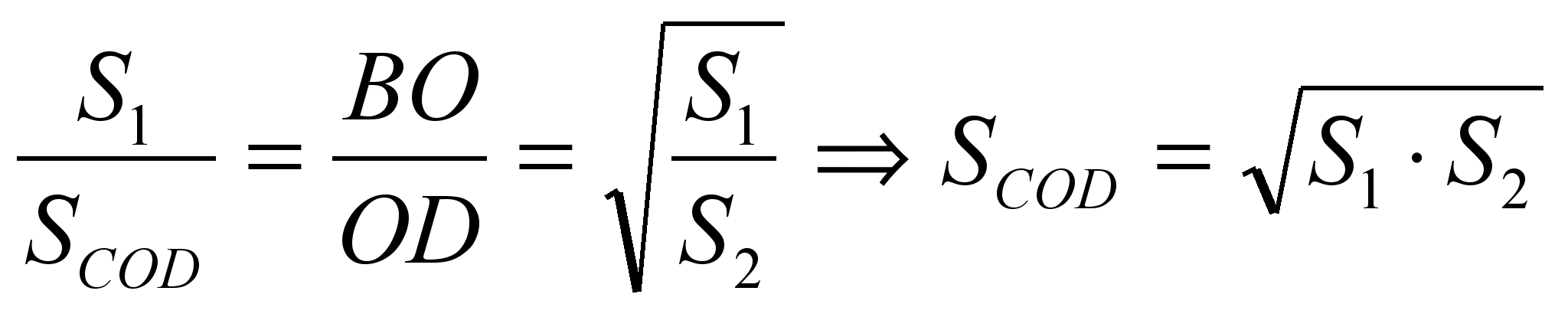 . Apoi
. Apoi
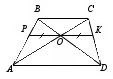
Folosind asemănarea, se poate demonstra proprietatea unui segment care trece prin punctul de intersecție al diagonalelor unui trapez paralel cu bazele. Invităm elevii să rezolve problema: „Fie O punctul de intersecție al diagonalelor trapezului ABCD cu temelii î.HrȘi ANUNȚ. , . Aflați lungimea segmentului PK trecând prin punctul de intersecție al diagonalelor trapezului paralel cu bazele. În ce segmente este împărțit? PK punct DESPRE».
În figură, ni s-a dat doar măsura unui unghi, așa că ar trebui să putem deduce mai multe informații pe baza acelui element. Deoarece patrulaterul este un trapez isoscel, știm că unghiurile de bază sunt congruente. Acum, să aflăm cât?
Împreună au un total de 128°. Reamintim teorema unghiului interior al poligonului conform căreia unghiurile interioare ale unui patrulater trebuie să fie de 360°. Deci, să încercăm să folosim acest lucru într-un mod care să ne ajute să definim o măsură? Mai întâi, să însumăm toate unghiurile și să le setăm la 360°.
De aici 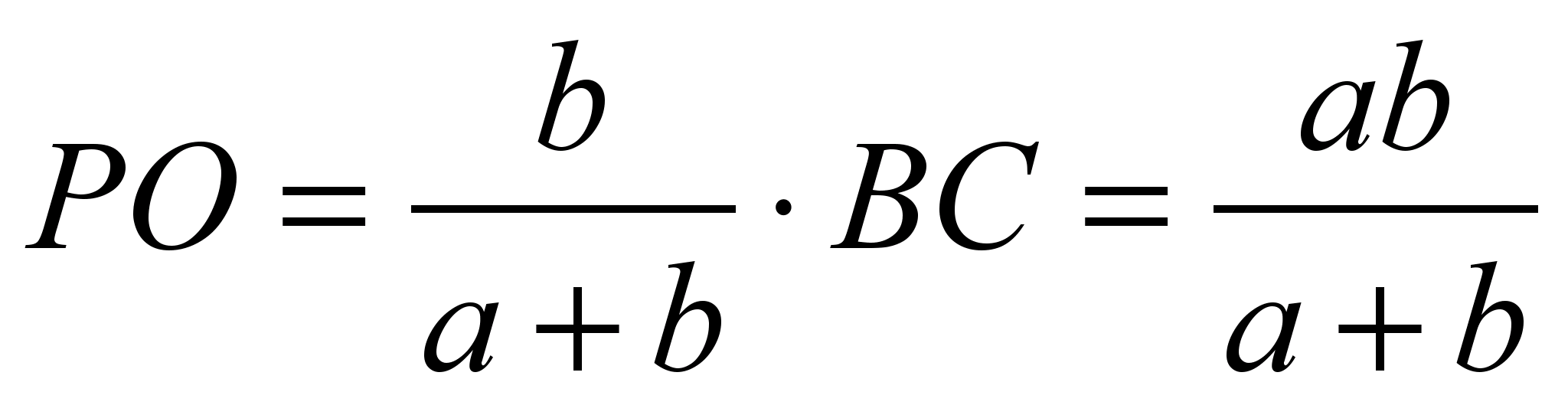 .
.
În mod similar, din asemănarea triunghiurilor D.O.K.Și DBC, urmează că 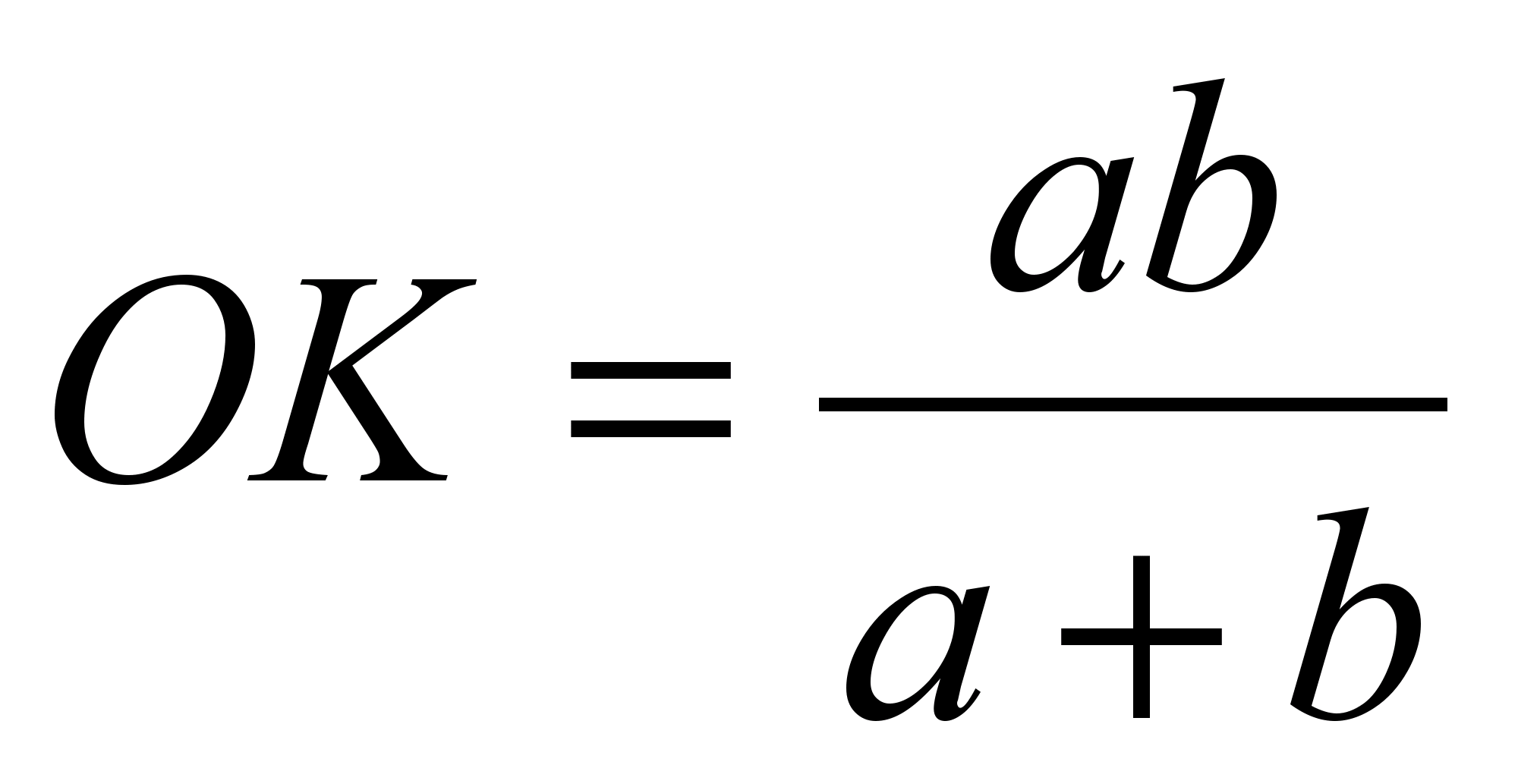 . De aici
. De aici 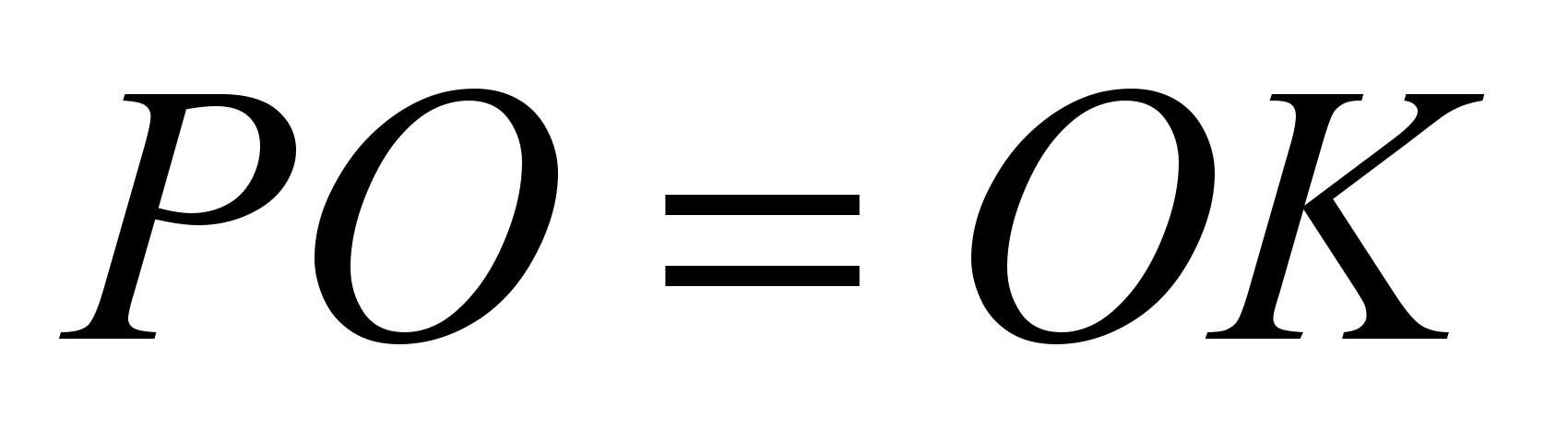 Și
Și 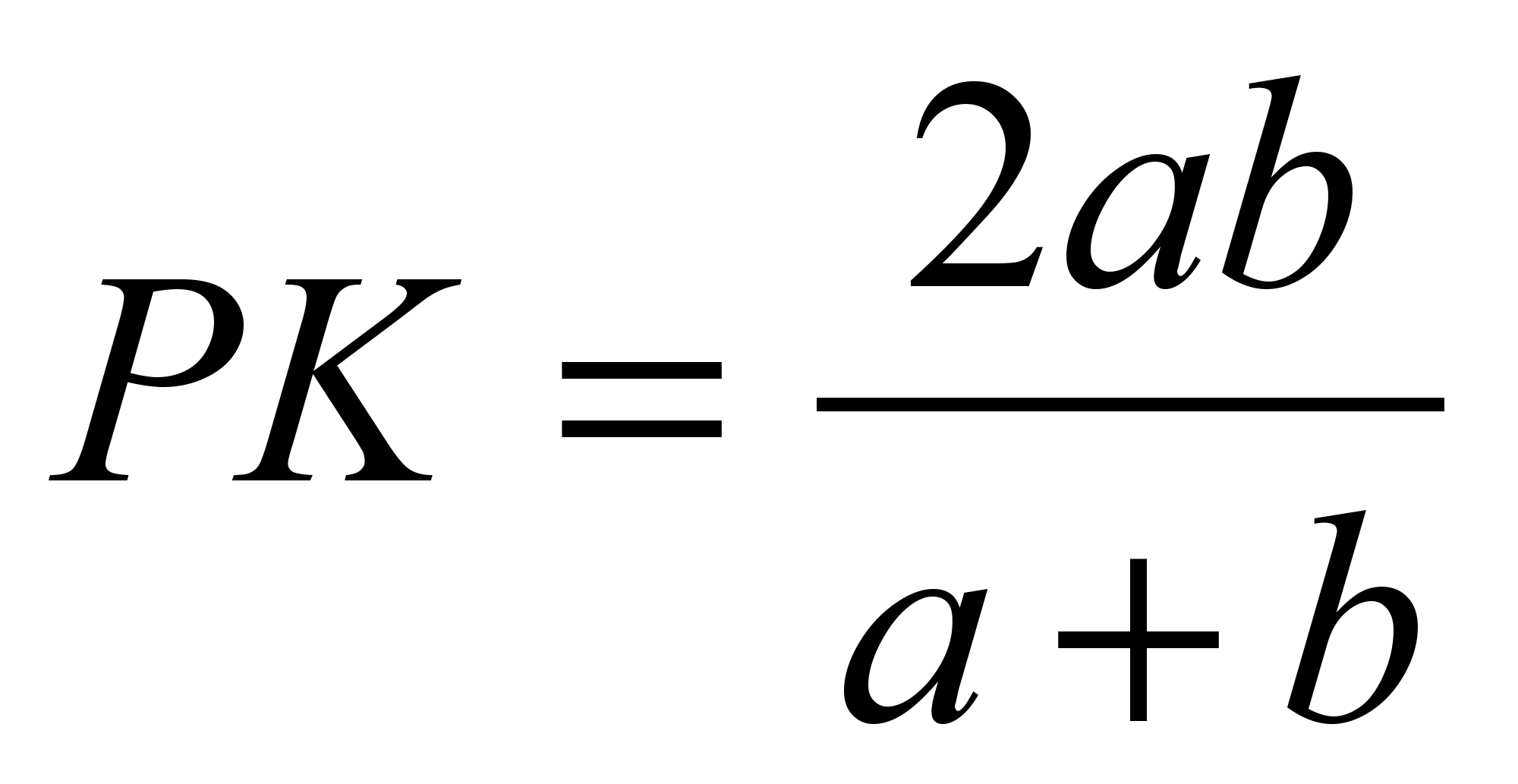 .
.
Circumscris în jurul unui trapez
Deci, dacă definim măsuri? Această valoare înseamnă că măsura? În cele din urmă, putem seta ca 116 să fie egal cu expresia prezentată în? Deși metoda de mai sus a fost o modalitate profundă de a rezolva exercițiul, am putea folosi pur și simplu proprietatea că unghiurile complementare ale trapezelor isoscele sunt complementare. Rezolvarea în acest fel este mult mai rapidă, deoarece trebuie doar să găsim care este complementul de 64°.
Odată ce ajungem la acest punct al problemei noastre, pur și simplu vom seta 116 la 4 și vom rezolva ca înainte. Ni s-a dat și asta? În trecut, am învățat câteva teoreme de congruență a triunghiului care pot fi aplicate în această situație dacă putem găsi doar o altă latură sau unghi care este congruent.
Îi facem pe elevi să realizeze proprietatea dovedită: un segment paralel cu bazele trapezului, care trece prin punctul de intersecție al diagonalelor și care leagă două puncte pe laturi, este împărțit la jumătate la punctul de intersecție al diagonalelor. Lungimea sa este media armonică a bazelor trapezului.
În continuare de la proprietatea a patru puncte:într-un trapez, punctul de intersecție al diagonalelor, punctul de intersecție al continuării laturilor, punctele medii ale bazelor trapezului se află pe aceeași linie.
Noua noastră ilustrație este prezentată mai jos. Mai jos este o dovadă geometrică pe două coloane a acestui exercițiu. Pentru a accesa geometrii precum. Nu te mai lupta și începe să înveți astăzi cu mii de resurse gratuite! Proprietățile sunt reprezentate prin link-uri către lecțiile corespunzătoare. Lecțiile sunt enumerate într-o ordine logică, ceea ce înseamnă că fiecare lecție se referă la cele anterioare. și nu se referă la el. Lista combină lecțiile corespunzătoare, care se află pe pagini diferite acest site.
Diagonalele și înălțimea unui trapez
Un trapez este isoscel dacă și numai dacă unghiurile sale de bază sunt congruente. Un trapez este isoscel dacă și numai dacă cele două diagonale ale sale sunt congruente. Linia mediană a unui trapez este paralelă cu bazele sale. Lungimea liniei mediane a unui trapez este jumătate din suma lungimilor bazelor sale. Într-un trapez, o secțiune a unei linii trasate de la mijlocul unei laturi laterale paralele cu bazele intersectează cealaltă parte la mijlocul ei.
Prezentându-le elevilor asemănarea figurilor (nu a triunghiurilor), putem oferi să găsim lungimea segmentului care împarte trapezul în două similare.
Prin urmare, un segment care împarte un trapez în două trapeze asemănătoare are lungimea egală cu media geometrică a lungimilor bazelor.
După derivarea formulei pentru aria unui trapez, este util să se demonstreze proprietatea unui segment care împarte un trapez în două zone egale.
Linia mediană a unui trapez este locul punctelor echidistante de cele două drepte care conțin bazele trapezului. Într-un trapez, suma unghiurilor interioare de la capetele laturii laterale este de 180°. Într-un trapez, linia mediană bisectează orice segment de linie care leagă un punct de pe o bază mai scurtă de un punct de pe o bază mai mare. Într-un trapez, distanța dintre punctele medii ale diagonalelor sale este jumătate din diferența dintre lungimile bazelor mai mari și mai scurte.
Dacă într-un trapez suma a două unghiuri interioare opuse este de 180°, atunci trapezul este isoscel. Într-un trapez isoscel, o linie care trece printr-o intersecție diagonală paralelă cu bazele traversează unghiul dintre diagonale. Într-un trapez isoscel, latura laterală este văzută la un unghi de la oricare dintre cele două vârfuri opuse.
Să facem un sistem 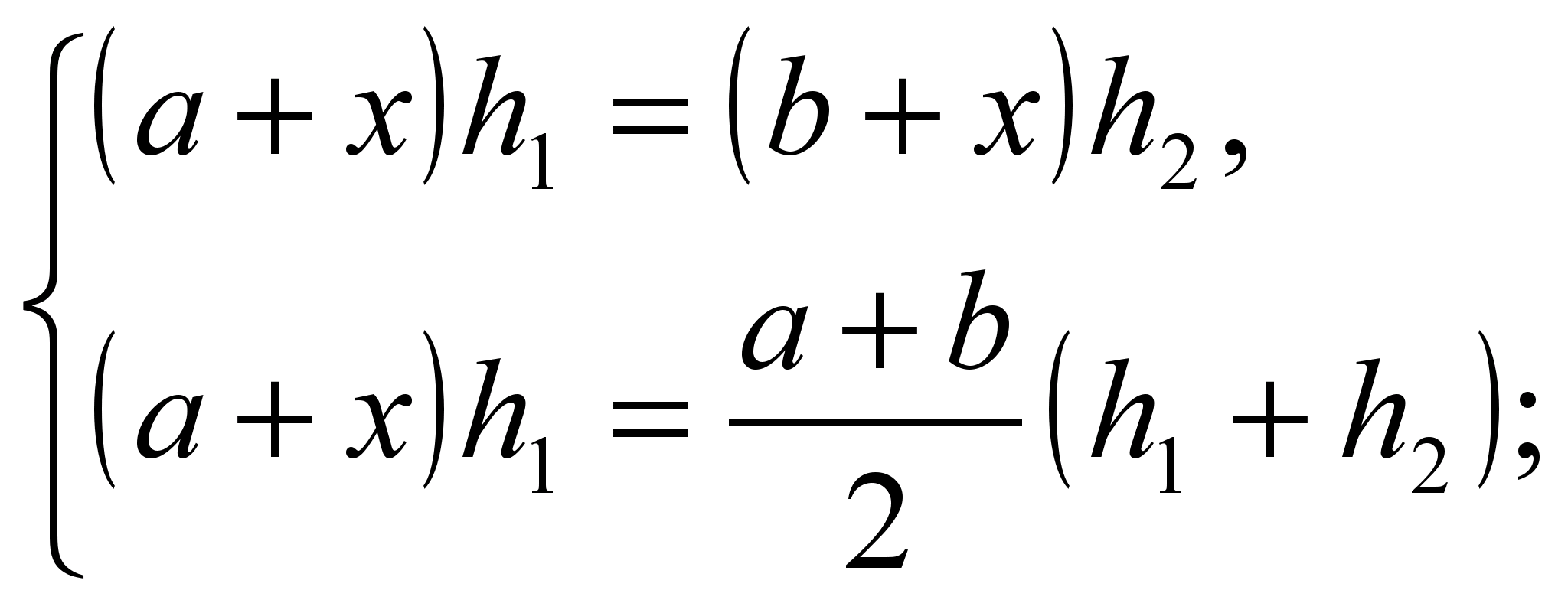
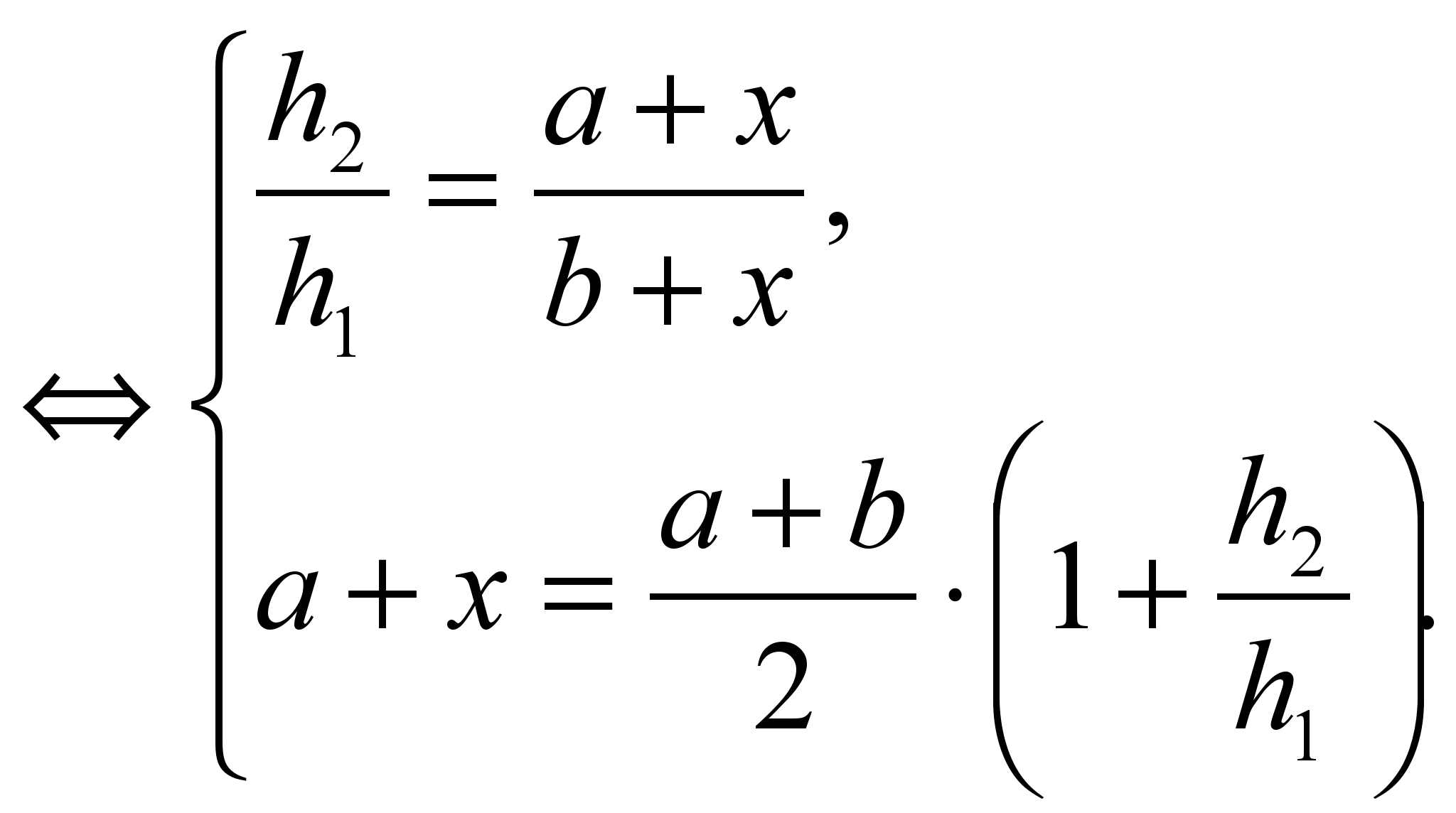
Soluție de sistem 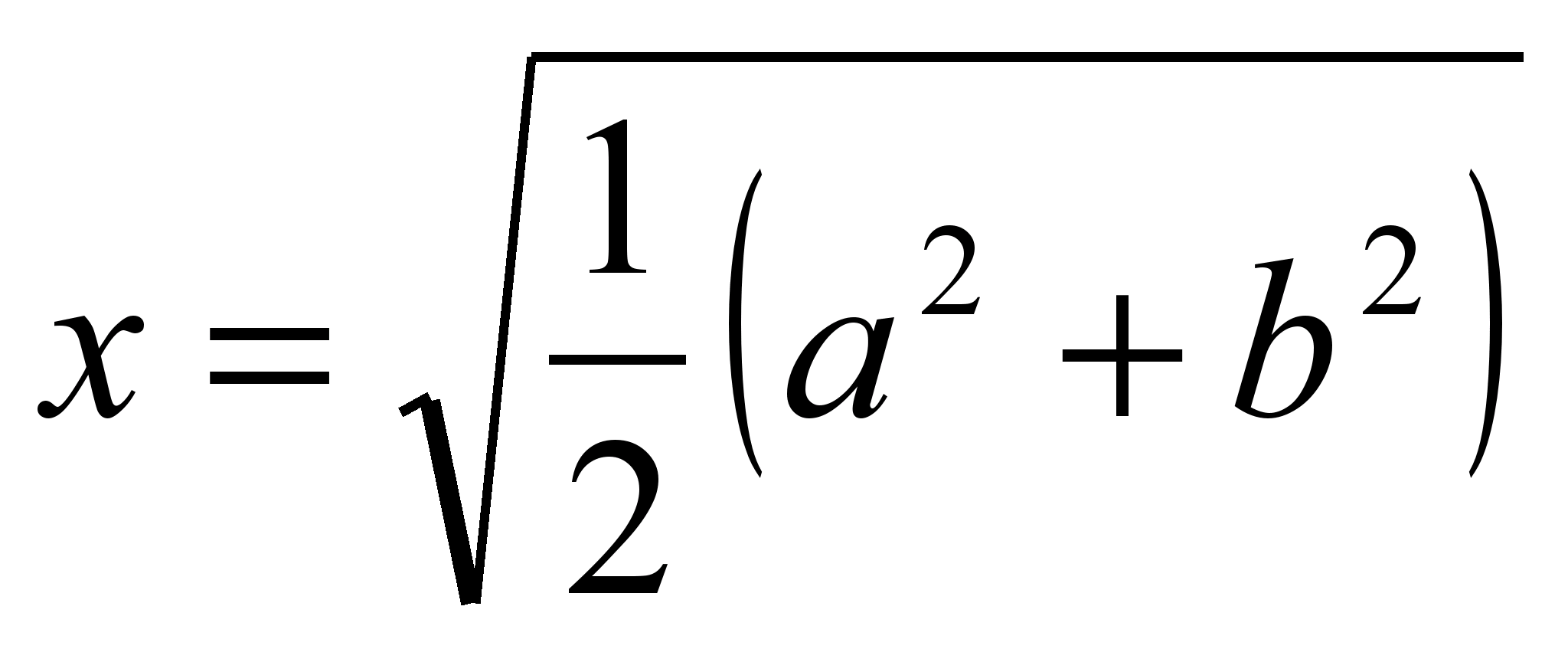 .
.
Prin urmare, lungimea segmentului care împarte trapezul în două egale este egală cu 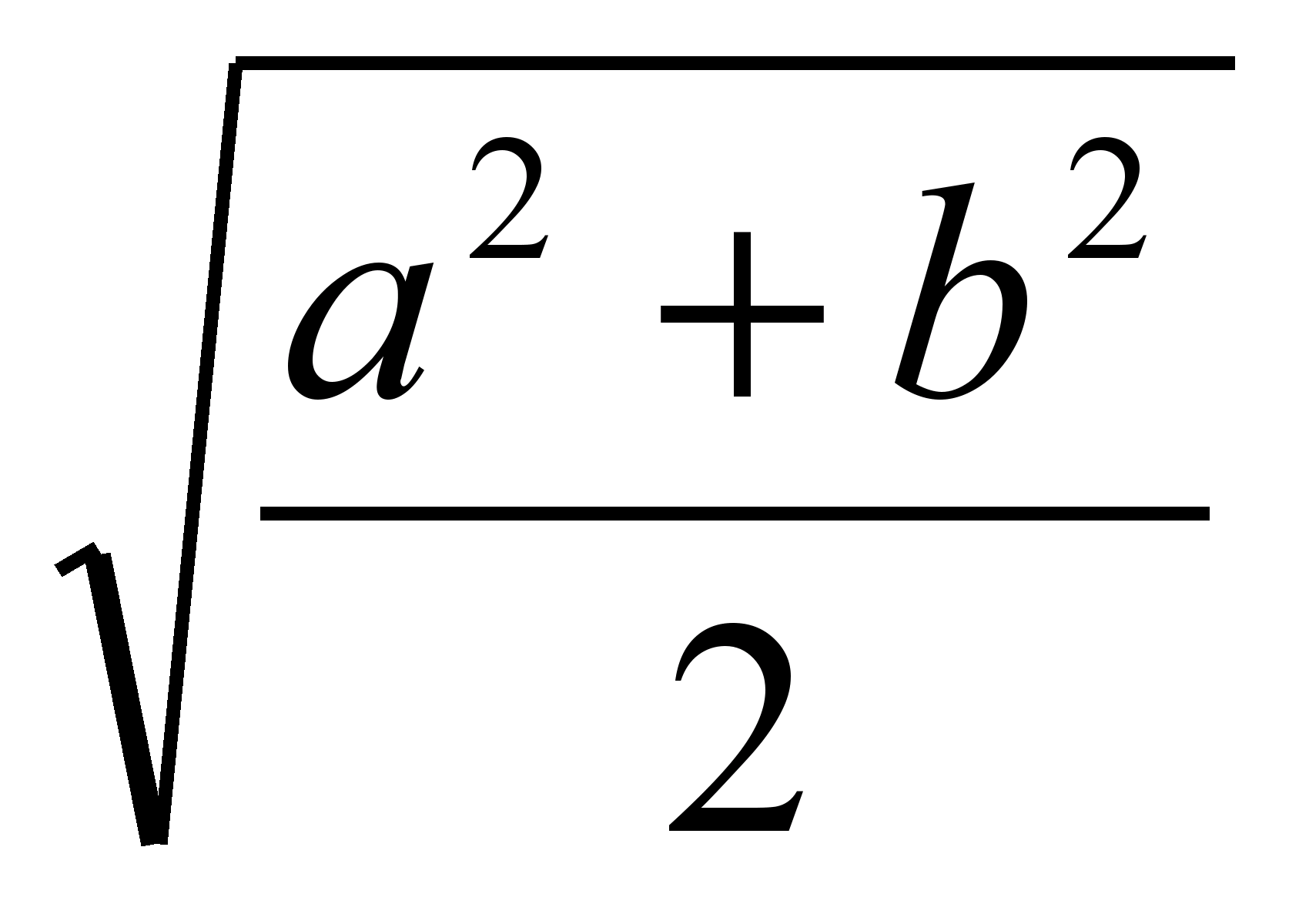 (lungimile pătrate medii ale bazelor).
).
(lungimile pătrate medii ale bazelor).
).
Lista de lecții este acum aceeași cu rezumatele scurte. Într-un trapez isoscel, unghiurile de bază sunt congruente. Teorema 2. Dacă unghiurile bazei dintr-un trapez sunt congruente, atunci trapezul este isoscel. Probleme rezolvate Într-un trapez isoscel, unghiul de bază este de 73°. Găsiți toate celelalte unghiuri ale trapezului. Într-un trapez isoscel, unghiul bazei este de trei ori unghiul intern de la capătul bazei mai scurte. Găsiți toate unghiurile trapezului.
Într-un trapez, un segment de dreaptă trasat de la mijlocul unei laturi paralele cu bazele intersectează cealaltă parte la mijlocul său. Aflați lungimea trapezului pe linia mediană. Într-un trapez, baza mare are 27 cm lungime și este cu 10 cm mai lungă decât baza.
Pentru ca elevii să realizeze legătura dintre segmentele indicate, li se cere să le construiască pentru un anumit trapez. Fără dificultate, elevii vor construi linia mediană a unui trapez și un segment care trece prin punctul de intersecție al diagonalelor trapezului paralel cu bazele. Unde vor fi al treilea și al patrulea segment? Răspunsul la această întrebare ar trebui să-i determine pe elevi să descopere relația dintre medii.
Aflați lungimile bazelor trapezoidale. Într-un trapez isoscel, cele două diagonale sunt congruente. Problema 2. Dacă două diagonale dintr-un trapez sunt congruente, atunci trapezul este isoscel. Problema 3. Orice punct de pe linia mediană a unui trapez este echidistant de două drepte paralele care conțin bazele trapezului. Dacă un punct dintr-un plan este echidistant de două drepte paralele care conțin bazele unui trapez, atunci punctul aparține dreptei care conține. trapez pe linia mediană. Problema rezolvata. Într-un trapez, orice segment de linie dreaptă care leagă un punct de pe o bază mai scurtă de un punct de pe o bază mai mare este tăiat în două la linia mediană a trapezului.
Atributul și proprietatea unui patrulater înscris și circumscris trebuie specificate pentru toate patrulaturile cunoscute de elevi, inclusiv pentru trapez.
Proprietățile trapezului descris. Un trapez poate fi descris despre un cerc dacă și numai dacă suma lungimilor bazelor este egală cu suma lungimilor laturilor.
Primul este evident. Pentru a demonstra al doilea corolar, este necesar să se stabilească că unghiul COD direct, ceea ce nu este mare lucru. Dar cunoașterea acestei consecințe ne permite să folosim un triunghi dreptunghic în rezolvarea problemelor.
Într-un trapez, bisectoarele unghiurilor interioare de la capetele laturii laterale se intersectează în unghi drept. Într-un trapez, bisectoarele unghiurilor interioare de la capetele laturii laterale se intersectează într-un punct situat pe linia mediană a trapezului. Problema 4. Într-un trapez isoscel, unghiul de bază este de 60 °. Demonstrați că lungimea mai scurtă a bazei este egală cu diferența dintre lungimea mai mare a bazei și lungimea laturii.
Într-un trapez isoscel, diagonala este de 10 cm și este de 60° cu baza. Aflați lungimea unui trapez de lungime medie. Bazele trapezului sunt lungi de 3 și 5 unități, o diagonală este perpendiculară pe latură, iar cealaltă diagonală traversează unghiul. pe o bază mai mare. Aflați înălțimea trapezului. Folosind o riglă și o busolă, construiți un trapez care are baze care se potrivesc cu cele două segmente date și laturi, congruent. alte două segmente date.
Să precizăm consecințele pentru trapez circumscris isoscel :
|
|
înălțimea unui trapez isoscel circumscris este media geometrică a bazelor trapezului. Diagonalele și unghiurile unui trapezFolosind o riglă și o busolă, construiți un trapez care are baze care se potrivesc cu cele două segmente și laturi date care sunt congruente. la alte două segmente date. Geometria este un subiect specific de matematică care se ocupă de forme și obiecte și problemele aferente acestora. Exista tipuri diferite forme geometrice. Câteva forme 2D importante sunt pătratul, dreptunghiul, triunghiul, poligonul, cercul, paralelogramul, trapezul, rombul și așa mai departe. o formă mărginită de patru laturi se numește patrulater. |
Luați în considerare principiile de bază ale metodologiei pentru studierea proprietăților unui trapez.
În primul rând, este utilizarea abordarea sarcinii . Nu este nevoie să se introducă noi proprietăți ale trapezului în cursul teoretic al geometriei. Aceste proprietăți sunt descoperite și formulate de către elevi prin rezolvarea problemelor (mai bine decât sistemele de probleme). Este important ca profesorul să știe ce sarcini trebuie stabilite și în ce moment al procesului de învățare. În plus, fiecare proprietate poate fi o sarcină cheie în sistemul de sarcini.
În al doilea rând, organizare „spirală” a studierii proprietăților unui trapez
. Puteți reveni la proprietățile individuale de mai multe ori, apoi este probabil ca studenții să le amintească. De exemplu, proprietatea a patru puncte poate fi demonstrată studiind asemănarea și apoi folosind vectori. Aria egală a triunghiurilor adiacente laturilor unui trapez poate fi demonstrată folosind ca proprietate a triunghiurilor având înălțimi egale, desenat pe laturile situate pe o linie dreaptă, și formula 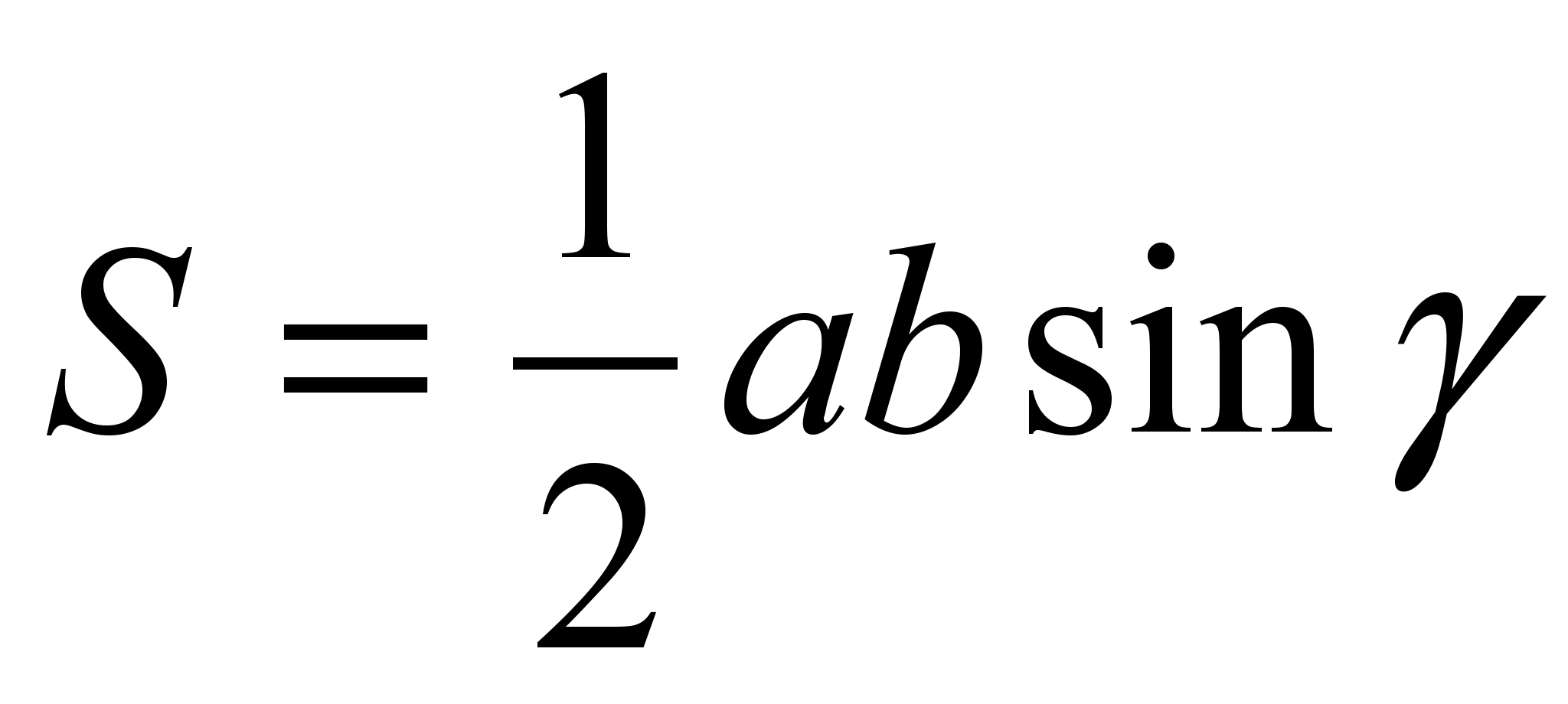 . Puteți calcula proprietățile unui triunghi dreptunghic pe trapezul circumscris, teorema sinusului pe trapezul înscris și așa mai departe.
. Puteți calcula proprietățile unui triunghi dreptunghic pe trapezul circumscris, teorema sinusului pe trapezul înscris și așa mai departe.
Includerea propusă a proprietăților „non-programe” ale trapezului în conținutul cursului de geometrie școlară, tehnologia sarcinilor pentru studierea lor, referirea repetată la proprietățile trapezului atunci când studiază alte subiecte va permite elevilor să înțeleagă mai profund trapezul și asigură succesul rezolvării problemelor privind aplicarea proprietăților sale.
Prin urmare, vom numi unul dintre ei mare
, al doilea - bază mică
trapez. Înălţime
un trapez poate fi numit orice segment al unei perpendiculare trasate de la vârfuri la latura opusă corespunzătoare (pentru fiecare vârf sunt două laturi opuse), închise între vârful luat și latura opusă. Dar se poate evidenția un fel special„înălțimi.
Definiția 8.
Înălțimea bazei unui trapez este segmentul unei linii drepte perpendiculare pe baze, închis între baze.
Teorema 7
. Linia mediană a trapezului este paralelă cu bazele și egală cu jumătate din suma acestora.
Dovada. Să fie date trapezul ABCD și linia mediană KM. Desenați o linie prin punctele B și M. Continuăm latura AD prin punctul D până se intersectează cu BM. Triunghiurile BCm și MPD sunt egale în latură și două unghiuri (CM=MD, ∠ BCM=∠ MDP - suprapunere, ∠ BMC=∠ DMP - vertical), prin urmare VM=MP sau punctul M este punctul de mijloc al BP. KM este linia mediană a triunghiului ABP. Conform proprietății liniei de mijloc a triunghiului, KM este paralel cu AP și în special AD și este egal cu jumătate din AP: 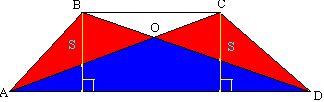 Teorema 8
. Diagonalele împart trapezul în patru părți, dintre care două, adiacente laturilor, sunt egale.
Teorema 8
. Diagonalele împart trapezul în patru părți, dintre care două, adiacente laturilor, sunt egale.
Permiteți-mi să vă reamintesc că cifrele se numesc egale dacă au aceeași zonă. Triunghiurile ABD și ACD sunt egale: au înălțimi egale (indicate cu galben) și o bază comună. Aceste triunghiuri au o parte comună AOD. Zona lor poate fi extinsă după cum urmează: 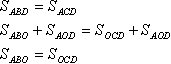
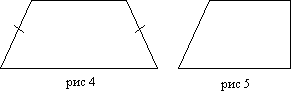 Tipuri de trapez:
Tipuri de trapez:
Definiția 9.
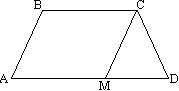
(Figura 1) Un trapez cu unghi ascuțit este un trapez în care unghiurile adiacente bazei mai mari sunt acute.
Definiția 10.
(Figura 2) Un trapez obtuz este un trapez în care unul dintre unghiurile adiacente bazei mai mari este obtuz.
Definiția 11.
(Figura 4) Un trapez se numește dreptunghiular, în care o latură este perpendiculară pe baze.
Definiția 12.
(Figura 3) Isoscel (isoscel, isoscel) este un trapez, în care laturile sunt egale.
 Proprietățile unui trapez isoscel:
Proprietățile unui trapez isoscel:
Teorema 10
. Unghiurile adiacente fiecăreia dintre bazele unui trapez isoscel sunt egale.
Dovada. Să demonstrăm, de exemplu, egalitatea unghiurilor A și D cu o bază mai mare AD a unui trapez isoscel ABCD. În acest scop, trasăm o dreaptă prin punctul C paralel cu latura laterală AB. Ea va intersecta baza mare în punctul M. Patrulaterul ABCM este un paralelogram, deoarece prin constructie are doua perechi de laturi paralele. Prin urmare, segmentul CM al dreptei secante cuprinse în interiorul trapezului este egal cu latura sa laterală: CM=AB. De aici este clar că CM=CD, triunghiul CMD este isoscel, ∠CMD=∠CDM, și, prin urmare, ∠A=∠D. Unghiurile adiacente bazei mai mici sunt de asemenea egale, deoarece sunt pentru cele găsite interne unilaterale și au o sumă de două linii. 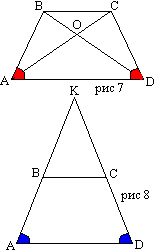 Teorema 11
. Diagonalele unui trapez isoscel sunt egale.
Teorema 11
. Diagonalele unui trapez isoscel sunt egale.
Dovada. Luați în considerare triunghiurile ABD și ACD. Este egal pe două laturi și unghiul dintre ele (AB=CD, AD este comun, unghiurile A și D sunt egale conform teoremei 10). Prin urmare AC=BD.
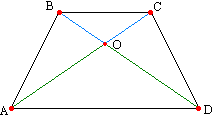 Teorema 13
. Diagonalele unui trapez isoscel sunt împărțite de punctul de intersecție în segmente egale corespunzător. Luați în considerare triunghiurile ABD și ACD. Este egal pe două laturi și unghiul dintre ele (AB=CD, AD este comun, unghiurile A și D sunt egale conform teoremei 10). Prin urmare, ∠ ОАD=∠ ОDA, prin urmare unghiurile ОВС și OSV sunt egale ca unghiuri suprapuse corespunzător ODA și ОАD. Reamintim teorema: dacă două unghiuri dintr-un triunghi sunt egale, atunci acesta este isoscel, prin urmare triunghiurile ОВС și ОAD sunt isoscele, ceea ce înseamnă OS=OB și ОА=OD etc.
Teorema 13
. Diagonalele unui trapez isoscel sunt împărțite de punctul de intersecție în segmente egale corespunzător. Luați în considerare triunghiurile ABD și ACD. Este egal pe două laturi și unghiul dintre ele (AB=CD, AD este comun, unghiurile A și D sunt egale conform teoremei 10). Prin urmare, ∠ ОАD=∠ ОDA, prin urmare unghiurile ОВС și OSV sunt egale ca unghiuri suprapuse corespunzător ODA și ОАD. Reamintim teorema: dacă două unghiuri dintr-un triunghi sunt egale, atunci acesta este isoscel, prin urmare triunghiurile ОВС și ОAD sunt isoscele, ceea ce înseamnă OS=OB și ОА=OD etc.
Un trapez isoscel este o figură simetrică.
Definiția 13.
Axa de simetrie a unui trapez isoscel se numește linie dreaptă care trece prin punctele medii ale bazelor sale.
Teorema 14
. Axa de simetrie a unui trapez isoscel este perpendiculară pe bazele sale. 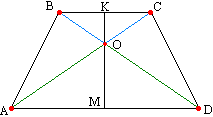 În teorema 9, am demonstrat că dreapta care unește punctele medii ale bazelor unui trapez trece prin punctul de intersecție al diagonalelor. În continuare (Teorema 13) am demonstrat că triunghiurile AOD și BOC sunt isoscele. OM și OK sunt medianele acestor triunghiuri, respectiv, prin definiție. Reamintim proprietatea unui triunghi isoscel: mediana unui triunghi isoscel, coborât la bază, este și înălțimea triunghiului. Datorită perpendicularității bazelor părților dreptei KM, axa de simetrie este perpendiculară pe baze.
În teorema 9, am demonstrat că dreapta care unește punctele medii ale bazelor unui trapez trece prin punctul de intersecție al diagonalelor. În continuare (Teorema 13) am demonstrat că triunghiurile AOD și BOC sunt isoscele. OM și OK sunt medianele acestor triunghiuri, respectiv, prin definiție. Reamintim proprietatea unui triunghi isoscel: mediana unui triunghi isoscel, coborât la bază, este și înălțimea triunghiului. Datorită perpendicularității bazelor părților dreptei KM, axa de simetrie este perpendiculară pe baze.
Semne care disting un trapez isoscel printre toate trapezele:
Teorema 15
. Dacă unghiurile adiacente uneia dintre bazele unui trapez sunt egale, atunci trapezul este isoscel.
Teorema 16
. Dacă diagonalele unui trapez sunt egale, atunci trapezul este isoscel.
Teorema 17
. Dacă laturile laterale ale trapezului, extinse până la intersecție, formează împreună cu baza sa mare un triunghi isoscel, atunci trapezul este isoscel.
Teorema 18
. Dacă un trapez poate fi înscris într-un cerc, atunci este isoscel.
Semnul unui trapez dreptunghiular:
Teorema 19
. Orice patrulater cu doar două unghiuri drepte la vârfuri adiacente este un trapez dreptunghic (este evident că cele două laturi sunt paralele, deoarece unilaterale sunt egale. în cazul în care trei unghiuri drepte sunt dreptunghi)
Teorema 20
. Raza unui cerc înscris într-un trapez este egală cu jumătate din înălțimea bazei. 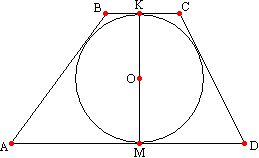 Dovada acestei teoreme este de a explica că razele trasate la baze se află la înălțimea trapezului. Din punctul O - centrul cercului ABCD înscris în acest trapez, trasăm razele până la punctele de contact cu bazele sale ale trapezului. După cum știți, raza trasată la punctul de contact este perpendiculară pe tangente, prin urmare OK ^ BC și OM ^ AD. Amintiți-vă teorema: dacă o dreaptă este perpendiculară pe una dintre drepte paralele, atunci este și perpendiculară pe a doua. Prin urmare, dreapta OK este de asemenea perpendiculară pe AD. Astfel, prin punctul O trec două drepte perpendiculare pe dreapta AD, care nu poate fi, prin urmare aceste drepte coincid și alcătuiesc perpendiculara comună KM, care este egală cu suma a două raze și este diametrul cercului înscris, deci r=KM/2 sau r=h/2.
Dovada acestei teoreme este de a explica că razele trasate la baze se află la înălțimea trapezului. Din punctul O - centrul cercului ABCD înscris în acest trapez, trasăm razele până la punctele de contact cu bazele sale ale trapezului. După cum știți, raza trasată la punctul de contact este perpendiculară pe tangente, prin urmare OK ^ BC și OM ^ AD. Amintiți-vă teorema: dacă o dreaptă este perpendiculară pe una dintre drepte paralele, atunci este și perpendiculară pe a doua. Prin urmare, dreapta OK este de asemenea perpendiculară pe AD. Astfel, prin punctul O trec două drepte perpendiculare pe dreapta AD, care nu poate fi, prin urmare aceste drepte coincid și alcătuiesc perpendiculara comună KM, care este egală cu suma a două raze și este diametrul cercului înscris, deci r=KM/2 sau r=h/2.
Teorema 21
. Aria unui trapez este egală cu produsul dintre jumătate din suma bazelor și înălțimea bazelor. 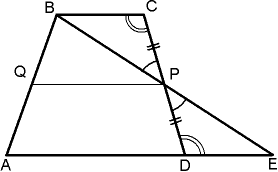
Dovada: Fie ABCD un trapez dat și AB și CD bazele sale. Fie și AH înălțimea coborâtă de la punctul A la linia CD. Atunci S ABCD = S ACD + S ABC .
Dar S ACD = 1/2AH CD și S ABC = 1/2AH AB.
Prin urmare, S ABCD = 1/2AH (AB + CD).
Q.E.D.
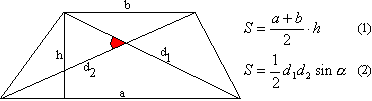 A doua formulă s-a mutat din patrulater.
A doua formulă s-a mutat din patrulater.
Ar putea fi util să citiți:
- Hadith cu instrucțiunile profetului Muhammad pe tema familiei;
- Sura de la daune și ochi. Recitare Dua pentru copii. Rugăciuni pentru diferite ocazii printre tătari;
- Videoclip despre postul în luna Ramadan;
- Lista literaturii folosite;
- Ce puncte forte ar trebui enumerate pe un CV?;
- Metode de diagnosticare a motivației personalității;
- Ce trebuie să știe subordonații?;
- Verbalizarea sentimentelor tale;
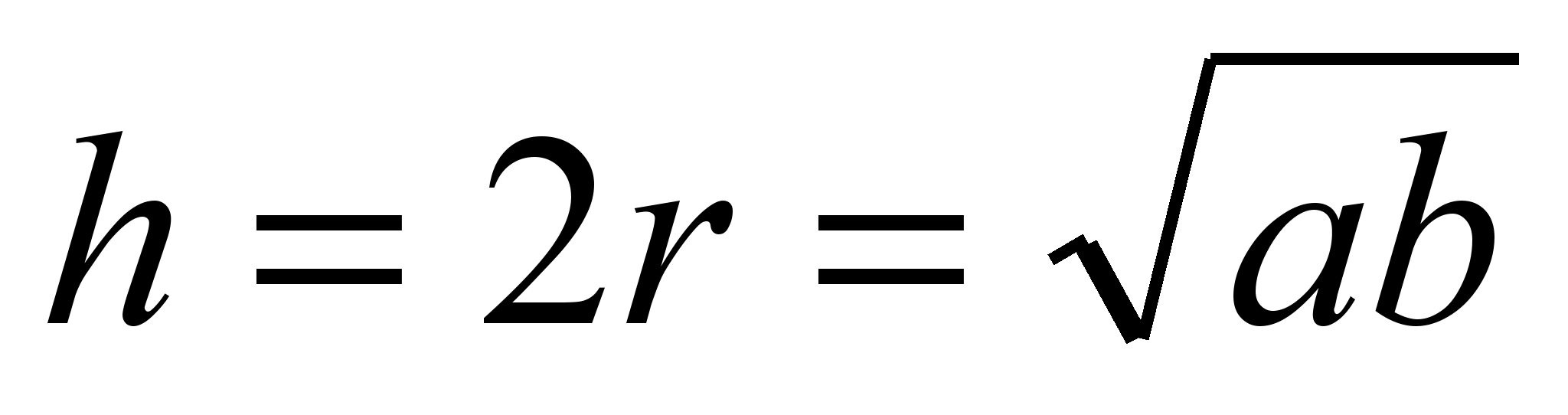 .
.