Oglišča trapeza. Gradivo o geometriji na temo "trapez in njegove lastnosti". Lastnosti enakokrakega trapeza
G.I. Kovaleva
METODA ZA PREUČEVANJE LASTNOSTI TRAPEZIJA
V gradivih različnih testov in izpitov se zelo pogosto srečujejo trapezne naloge, katerih rešitev od študentov zahteva poznavanje "neprogramskih" lastnosti trapeza. (Lastnosti veljajo za srednja črta trapez, lastnosti diagonal in kotov enakokrakega trapeza.) Katere izjemne lastnosti ima trapez? Kje in kdaj jih preučiti v šolskem tečaju geometrije?
Metoda za preučevanje lastnosti trapeza
Zdaj, ko smo videli več vrst, se poučimo o oblikah, ki nimajo lastnosti paralelogramov. Spomnimo se, da so paralelogrami štirikotniki, katerih nasprotni stranici sta vzporedni. V tem razdelku bomo obravnavali štirikotnike, katerih nasprotne stranice se lahko sekajo v neki točki. Začnimo naše raziskovanje s preučevanjem nekaterih lastnosti trapeza. Opredelitev. Trapez je štirikotnik s točno enim parom vzporednih stranic.
Po študiju lastnosti srednje črte trapeza lahko oblikujemo in dokažemo lastnost odseka, ki povezuje razpolovišča diagonal trapeza. Odsek, ki povezuje razpoloviščni točki diagonal trapeza, je enak polovični razliki osnov.
Pri vadbi glavne tehnike za reševanje problemov na trapezu "risanje dveh višin" morajo učenci ponuditi nalogo: "Naj BT- višina enakokraki trapez ABCD z razlogi pr. n. št in AD.
 ,
,
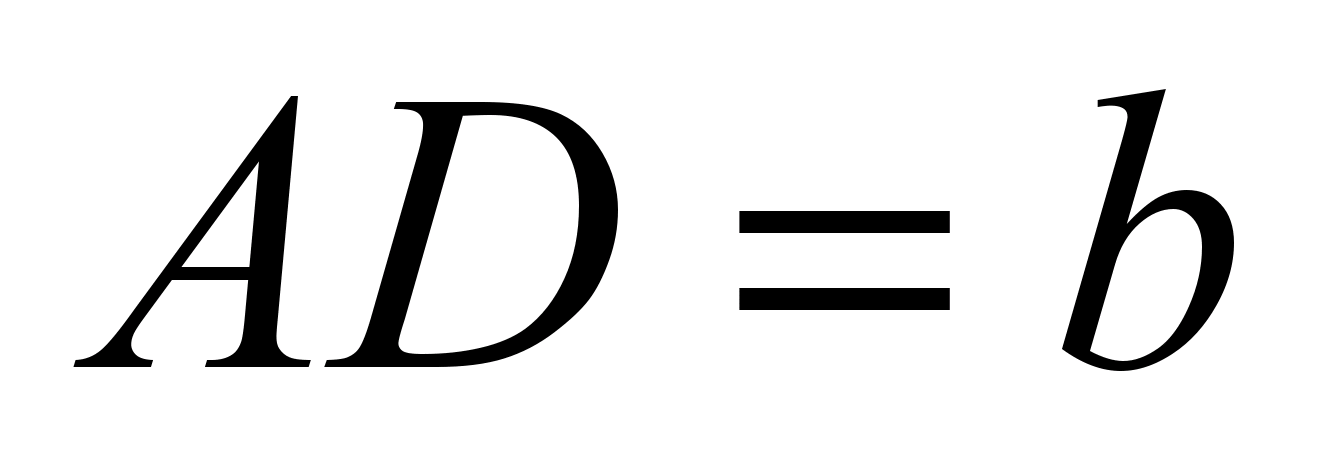 . Poiščite dolžine segmentov AT in TD».
. Poiščite dolžine segmentov AT in TD».
"Uporaba trigonometrije pri reševanju planimetričnih problemov"
Ker mora imeti trapez točno en par vzporednih stranic, bomo morali dokazati, da je en par nasprotnih stranic vzporeden, drugi pa ni v naši. Če pozabimo dokazati, da en par nasprotnih stranic ni vzporeden, ne izključujemo možnosti, da je štirikotnik paralelogram. Zato bo ta korak nujno potreben, ko delamo na različnih vajah, ki vključujejo trapez.
Preden se potopimo naravnost v našo študijo trapezov, bomo morali poznati imena različnih delov teh štirikotnikov, da bomo natančno določili njegove stranice in kote. Vsi trapezi vsebujejo dva glavna dela: podlago in noge. Nasprotni stranici trapeza, ki sta med seboj vzporedni, imenujemo osnove. Druge stranice trapeza, ki se na neki točki sekajo, če jih podaljšamo, imenujemo noge trapeza.
Tema "Podobnost figur" je zelo koristna za preučevanje lastnosti trapeza. Na primer, diagonale trapeza ga delijo na štiri trikotnike, trikotniki, ki mejijo na osnove, so podobni, trikotniki, ki mejijo na stranice, pa so enaki. Recimo tej izjavi zlastnost trikotnikov, na katere je trapez razdeljen s svojimi diagonalami. Poleg tega je prvi del trditve zelo enostavno dokazati preko znaka podobnosti trikotnikov v dveh kotih. Drugi del lahko študentom ponudimo v obliki naloge.
Podobnost oblikovanih trapeznih trikotnikov
Zgornja in spodnja stran trapeza potekata vzporedno ena z drugo, torej sta osnovi trapeza. Drugi stranici trapeza se sekata, če sta podaljšani, zato sta kraka trapeza. Odsek, ki povezuje središčni točki krakov trapeza, se imenuje srednji odsek. Dolžina tega segmenta je vedno enaka polovici vsote trapeznih osnov oz.
Razmerje dolžin segmentov in baz
Meritev srednjega segmenta je odvisna samo od dolžine trapeznih baz. Vendar pa obstaja pomembna lastnost da so nekateri trapezi odvisni izključno od njenih nog. Poglejmo zdaj te trapeze. Enakokraki trapez je trapez, katerega kraka sta skladna. Če ima štirikotnik natanko en par vzporednih premic, je po definiciji štirikotnik trapez. Definicija enakokrakega trapeza dodaja še eno specifikacijo: noge trapeza morajo biti skladne.
Prav tako trikotniki
BOC in AOB imajo skupno višino, če za njihove osnove vzamemo segmente CO in OA.
Potem 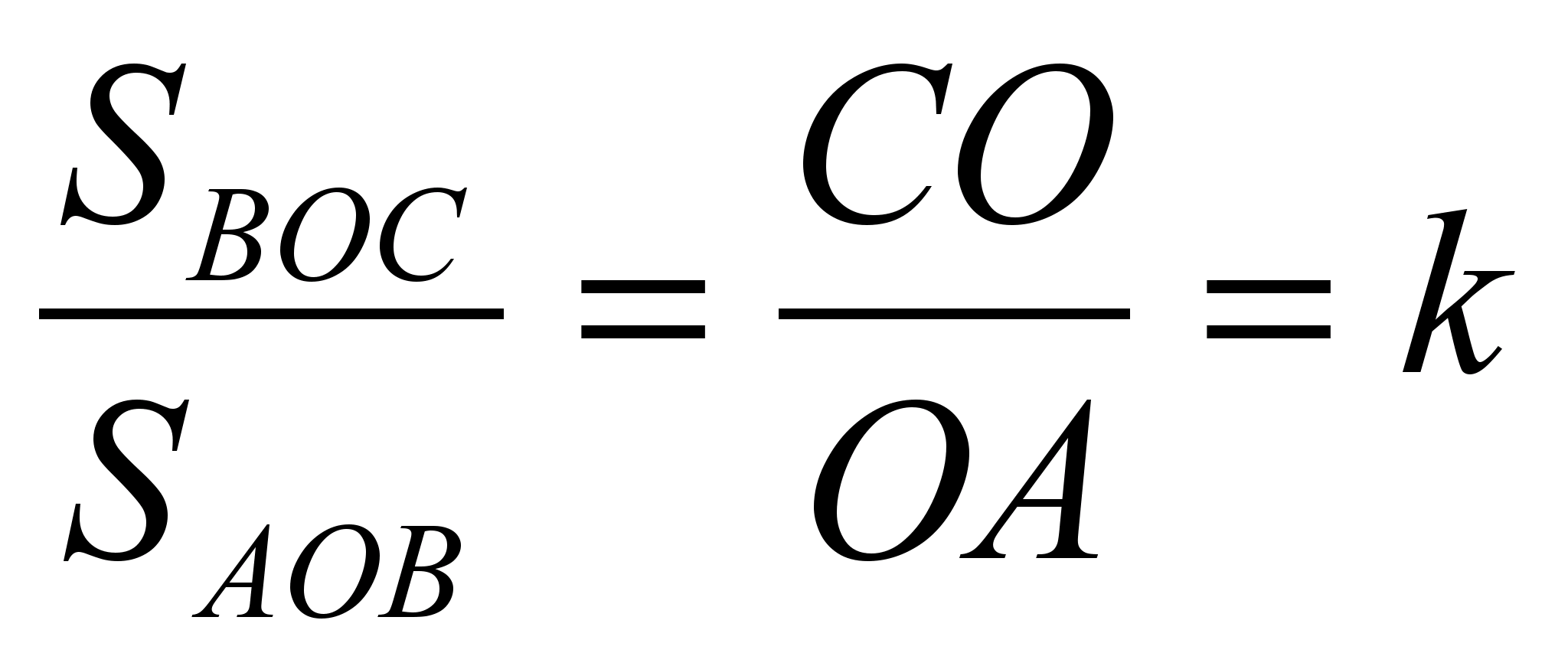 in
in 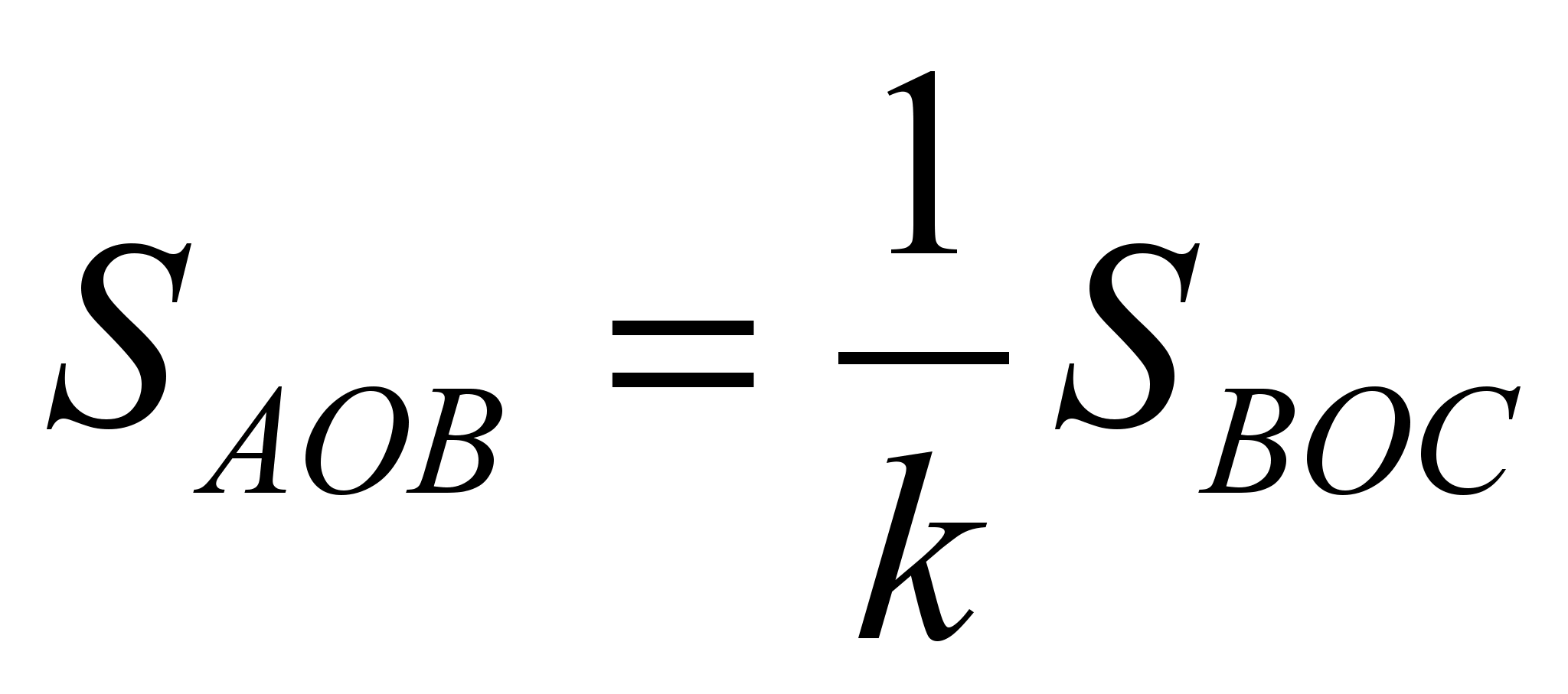 .
.
Iz teh dveh trditev izhaja, da 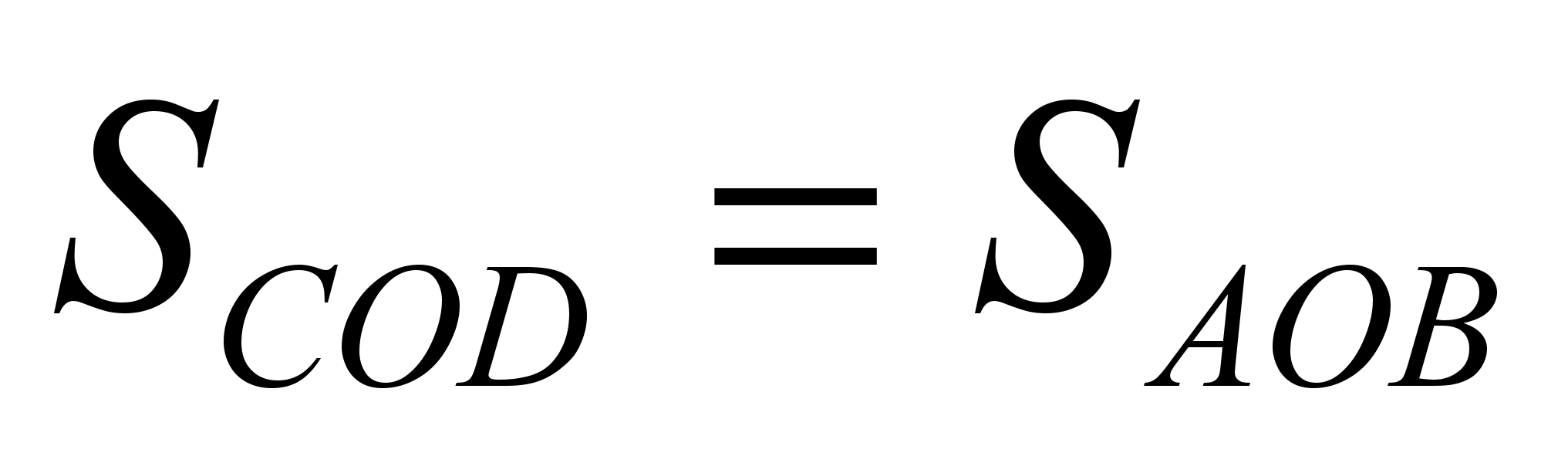 .
.
Obstaja več izrekov, ki nam lahko pomagajo dokazati, da je trapez enakokrak. Te lastnosti so navedene spodaj. Trapez je enakokrak, če in samo če sta kota pri osnovnici skladna. Trapez je enakokrak, če in samo če sta diagonali skladni.
Če je trapez enakokrak, potem sta njegova nasprotna kota komplementarna. Zmaj je štirikotnik z dvema različnima paroma sosednjih stranic, ki sta skladni. Spomnimo se, da so imeli tudi paralelogrami pare skladnih stranic. Vendar sta bili njuni skladni strani vedno nasprotni. Zmaji imajo dva para skladnih strani, ki se srečata na dveh različnih točkah. Oglejmo si spodnjo ilustracijo, da bomo lažje razumeli, kako izgleda zmaj.
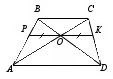
Bilo bi super, če se ne bi zadrževali na formulirani izjavi, ampak našli razmerje med ploščinami trikotnikov, na katere je trapez razdeljen z diagonalami
, ki povabi učence k rešitvi naloge: »Naj bo O presečišče diagonal trapeza. ABCD z razlogi pr. n. št in AD. Znano je, da površine trikotnikov BOC in AOD enako oz  in
in 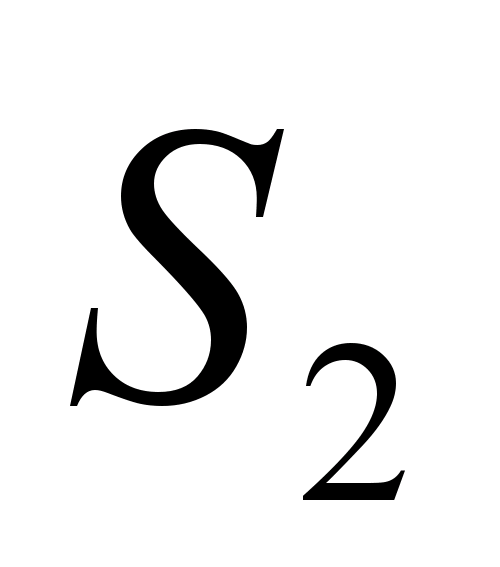 . Poiščite območje trapeza.
. Poiščite območje trapeza.
Zmaji imajo več lastnosti, po katerih jih bomo lažje prepoznali od drugih štirikolesnikov. Diagonali zmaja se stikata pod pravim kotom. Zmaji imajo točno en par nasprotnih kotov, ki sta skladna. Ti dve lastnosti sta prikazani na spodnjem diagramu.
To je naš edini par skladnih kotov, kajti? Pustite, da vaja reši nekaj težav, ki zahtevajo uporabo lastnosti trapeza in zmajev, o katerih smo pravkar izvedeli. Ker so nam podane dolžine osnov trapeza, lahko ugotovimo, kolikšna mora biti dolžina srednjega segmenta. Uporabimo formulo, ki smo jo podali za srednji segment, da to ugotovimo.
Ker . Torej iz podobnosti trikotnikov BOC in AOD temu sledi 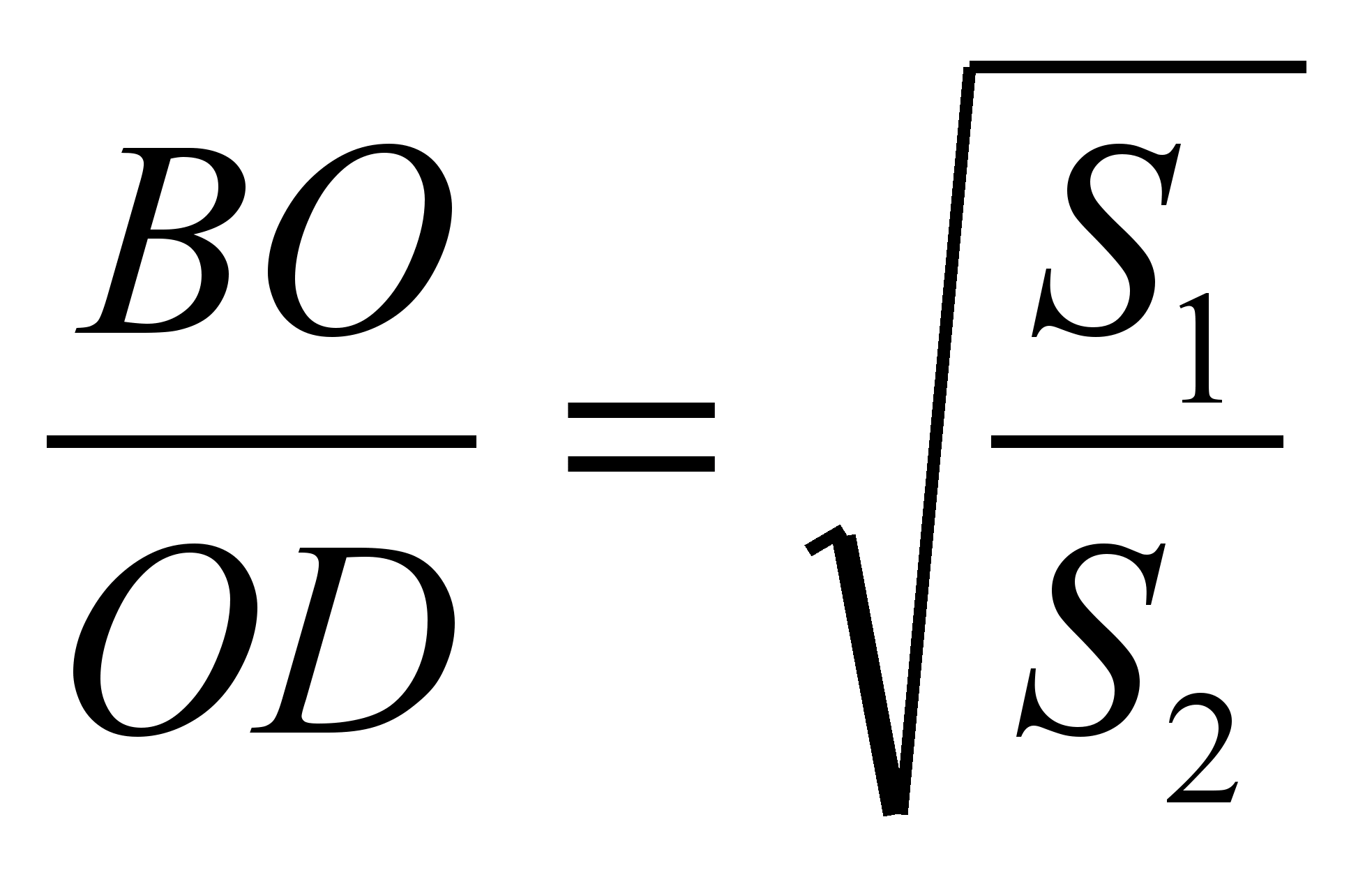 .Zato,
.Zato, 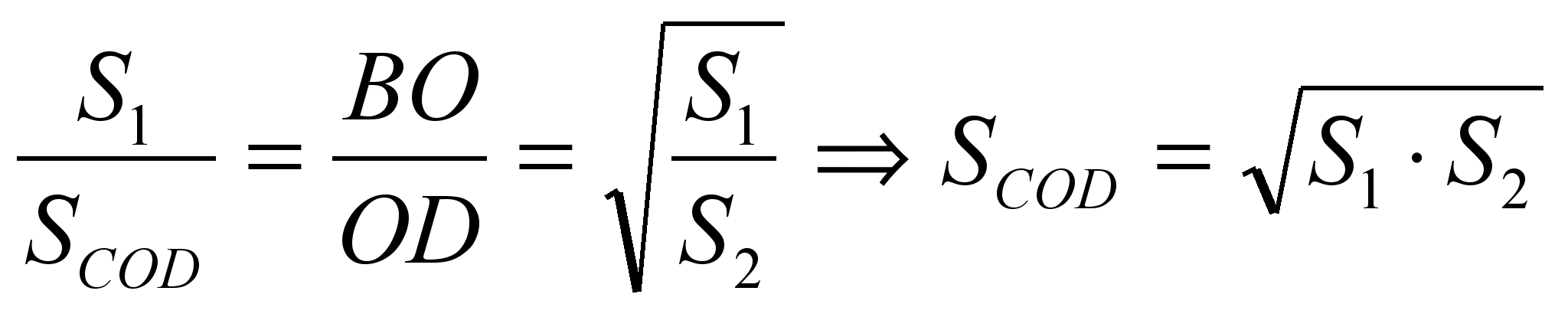 . Potem
. Potem
S podobnostjo je mogoče tudi dokazati Lastnost segmenta, ki poteka skozi presečišče diagonal trapeza, vzporednega z osnovami. Učence povabimo k rešitvi naloge: »Naj bo O presečišče diagonal trapeza. ABCD z razlogi pr. n. št in AD. , . Poišči dolžino odseka PK ki poteka skozi presečišče diagonal trapeza vzporedno z osnovami. Na katere segmente je razdeljen? PK pika O».
Na sliki smo dobili samo mero enega kota, zato bi morali imeti možnost sklepati več informacij na podlagi tega enega elementa. Ker je štirikotnik enakokraki trapez, vemo, da sta osnovna kota skladna. Zdaj pa ugotovimo, koliko?
Skupaj imata skupaj 128°. Spomnimo se izreka o notranjem kotu mnogokotnika, da morajo biti notranji koti štirikotnika 360°. Torej poskusimo to uporabiti tako, da nam bo pomagalo definirati mero? Najprej seštejmo vse kote in nastavimo na 360°.
Od tod 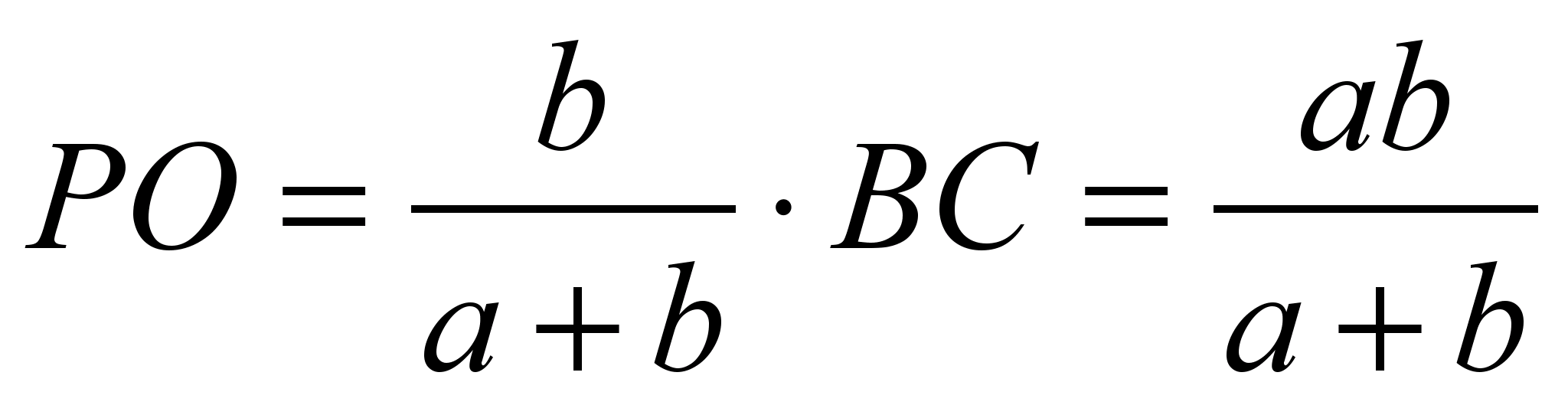 .
.
Podobno iz podobnosti trikotnikov D.O.K. in DBC, temu sledi 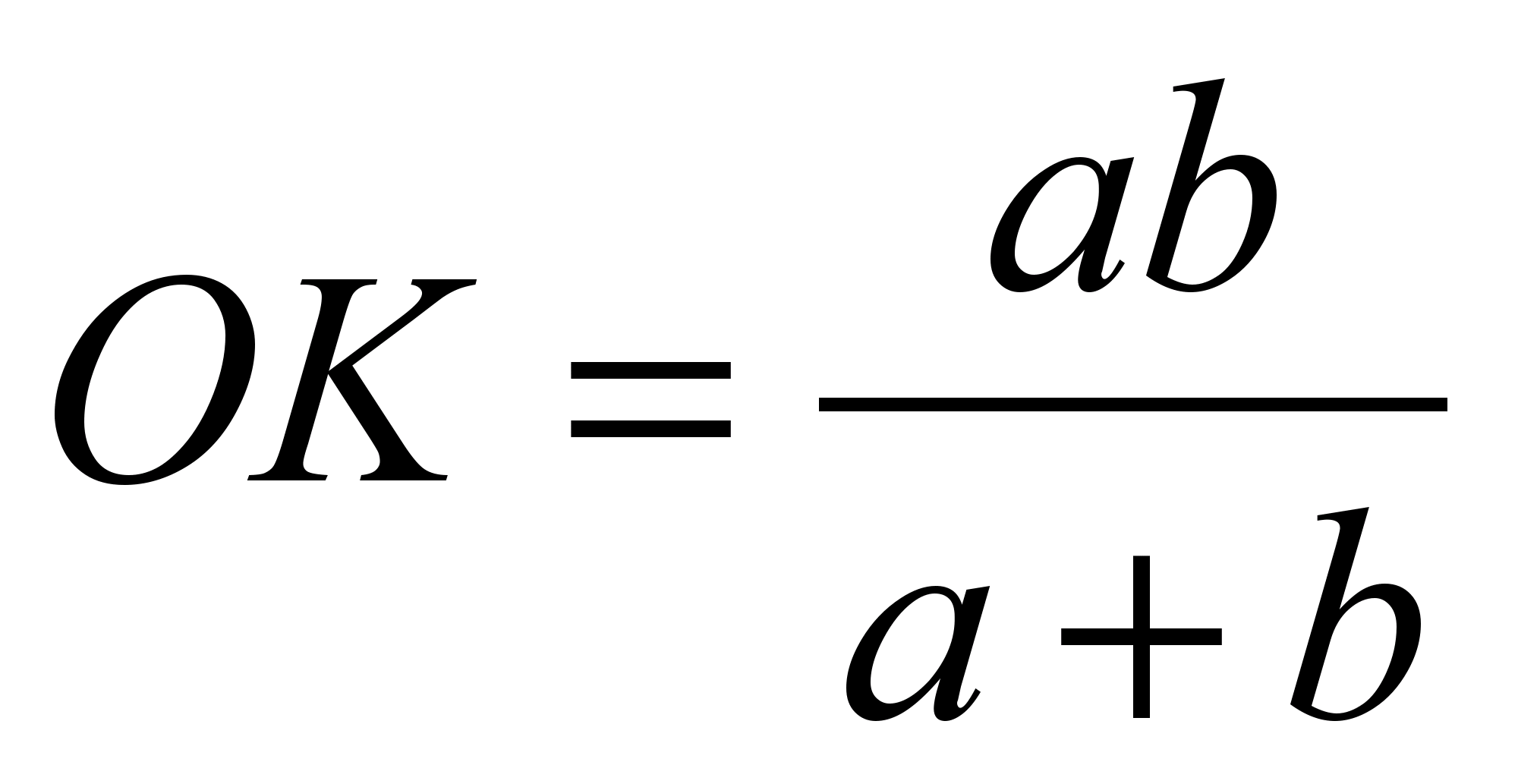 . Od tod
. Od tod 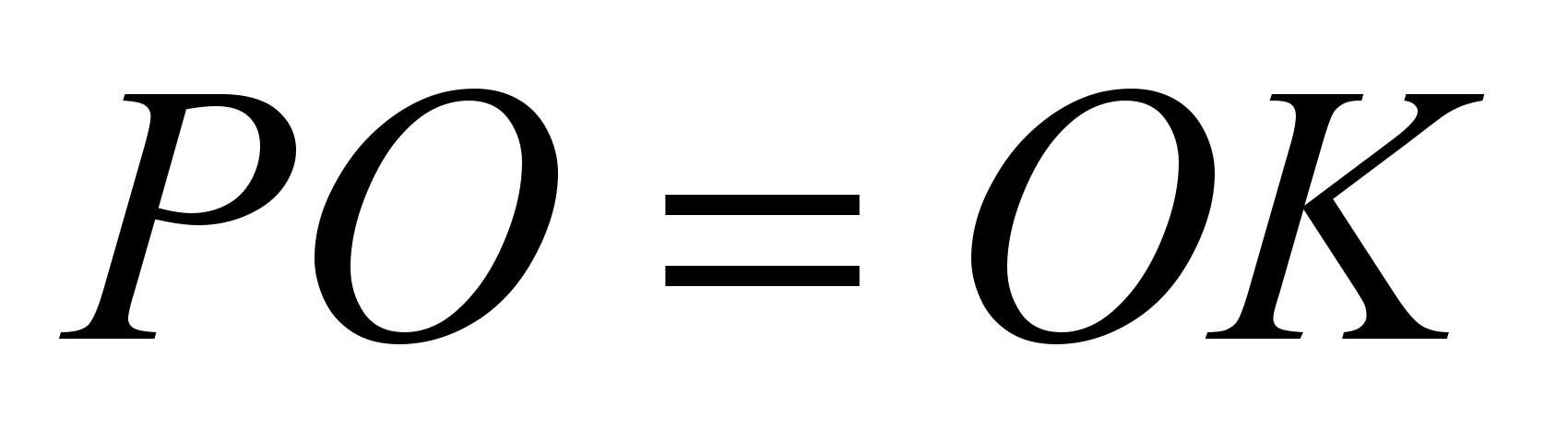 in
in 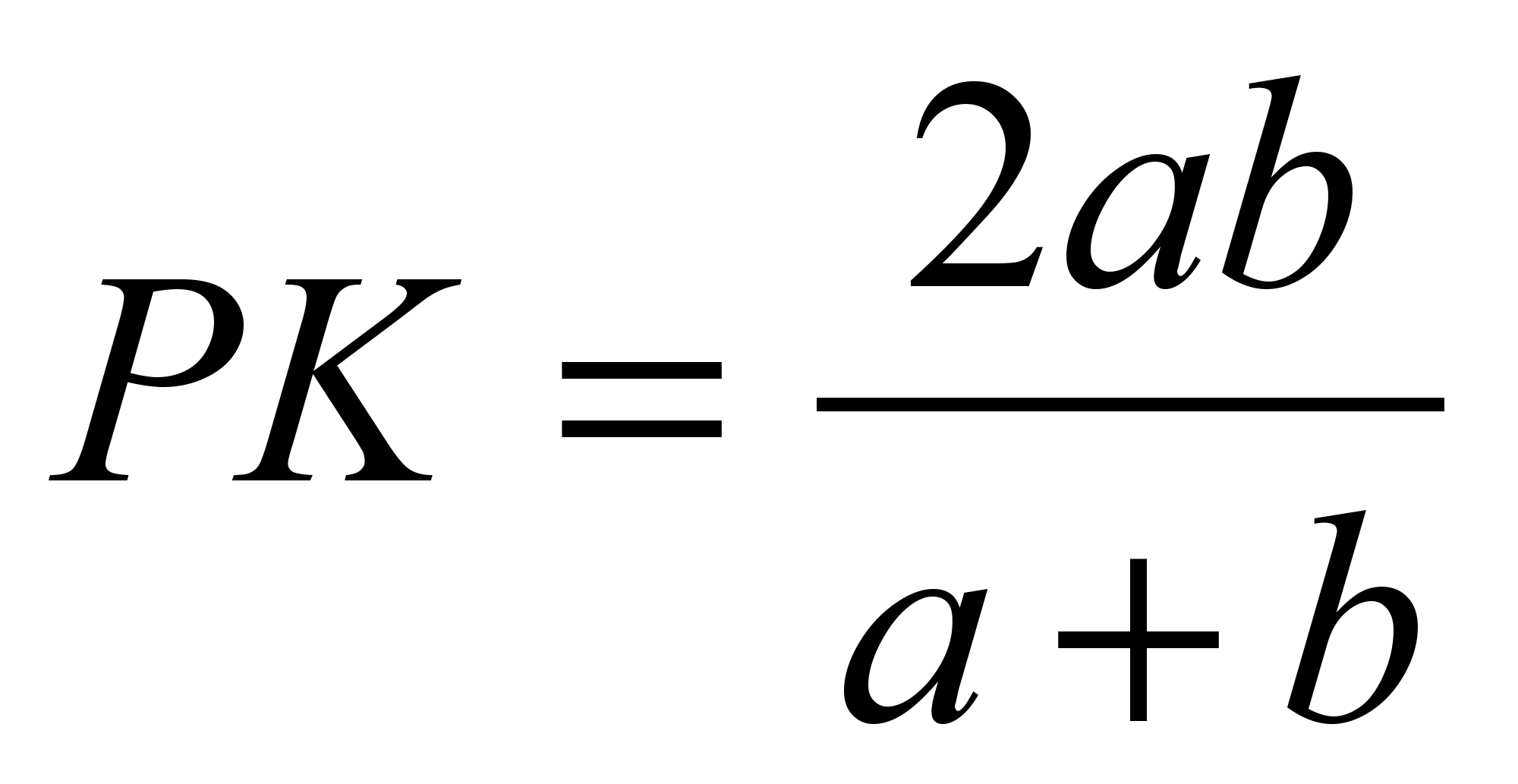 .
.
Okrožen okoli trapeza
Če torej opredelimo ukrepe? Ta vrednost pomeni, da je ukrep? Končno lahko nastavimo, da je 116 enako izrazu, prikazanem v? Čeprav je bila zgornja metoda globok način za rešitev vaje, bi lahko preprosto uporabili lastnost, da so komplementarni koti enakokrakih trapezov komplementarni. Reševanje na ta način je veliko hitrejše, saj moramo le najti, koliko je 64° komplement.
Ko pridemo do te točke v našem problemu, bomo preprosto nastavili 116 na 4 in reševali kot prej. Tudi to nam je bilo dano? V preteklosti smo se naučili več izrekov o skladnosti trikotnika, ki jih je mogoče uporabiti v tej situaciji, če le lahko najdemo drugo stran ali kot, ki je skladen.
Učence pripravimo do spoznanja dokazane lastnosti: odsek, ki je vzporeden z osnovami trapeza, ki poteka skozi presečišče diagonal in povezuje dve točki na stranicah, je razdeljen s presečiščem diagonal na pol. Njegova dolžina je harmonična sredina osnov trapeza.
Naprej od lastnost štirih točk: v trapezu ležijo presečišče diagonal, presečišče nadaljevanja stranic, razpolovišča osnov trapeza na isti premici.
Naša nova ilustracija je prikazana spodaj. Spodaj je geometrijski dokaz te vaje v dveh stolpcih. Za dostop do geometrij, kot je. Nehajte se kregati in se začnite učiti že danes s tisoči brezplačnih virov! Lastnosti so predstavljene s povezavami do ustreznih lekcij. Lekcije so navedene v logičnem vrstnem redu, kar pomeni, da se vsaka lekcija navezuje na prejšnje. in se ne nanaša na to. Seznam združuje ustrezne lekcije, ki se nahajajo na različne strani to spletno mesto.
Diagonale in višina trapeza
Trapez je enakokrak, če in samo če sta njegova osnovna kota skladna. Trapez je enakokrak, če in samo če sta njegovi diagonali skladni. Srednja črta trapeza je vzporedna z njegovimi osnovami. Dolžina srednje črte trapeza je polovica vsote dolžin njegovih osnov. V trapezu odsek premice, ki poteka iz sredine stranske stranice vzporedno z osnovami, seka drugo stranico na njeni sredini.
Če učence seznanimo s podobnostjo figur (ne trikotnikov), lahko ponudimo iskanje dolžine segmenta, ki deli trapez na dva podobna.
torej odsek, ki deli trapez na dva podobna trapeza, ima dolžino, ki je enaka geometrični sredini dolžin osnov.
Po izpeljavi formule za območje trapeza je koristno dokazati lastnost odseka, ki deli trapez na dve enaki ploskvi.
Srednja črta trapeza je geometrijsko mesto točk, ki so enako oddaljene od dveh premic, ki vsebujeta osnovici trapeza. V trapezu je vsota notranjih kotov na koncih stranske stranice 180°. V trapezu sredinska črta razpolavlja kateri koli odsek, ki povezuje točko na krajši osnovi s točko na večji osnovi. V trapezu je razdalja med središči njegovih diagonal polovica razlike v dolžinah večje in krajše osnove.
Če je v trapezu vsota dveh nasprotnih notranjih kotov 180°, potem je trapez enakokrak. V enakokrakem trapezu premica, ki poteka skozi presečišče diagonal vzporedno z osnovami, razpolavlja kot med diagonalama. V enakokrakem trapezu je stranska stranica vidna pod enim kotom iz enega od obeh nasprotnih oglišč.
Naredimo sistem 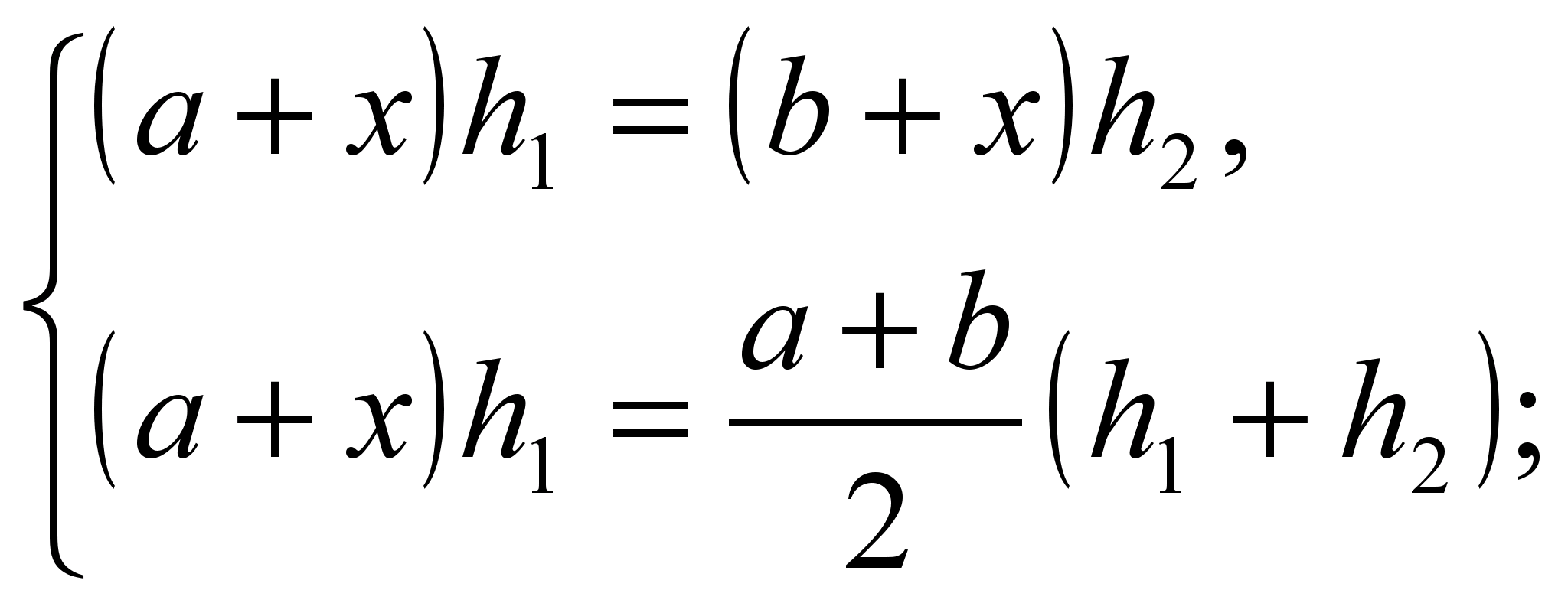
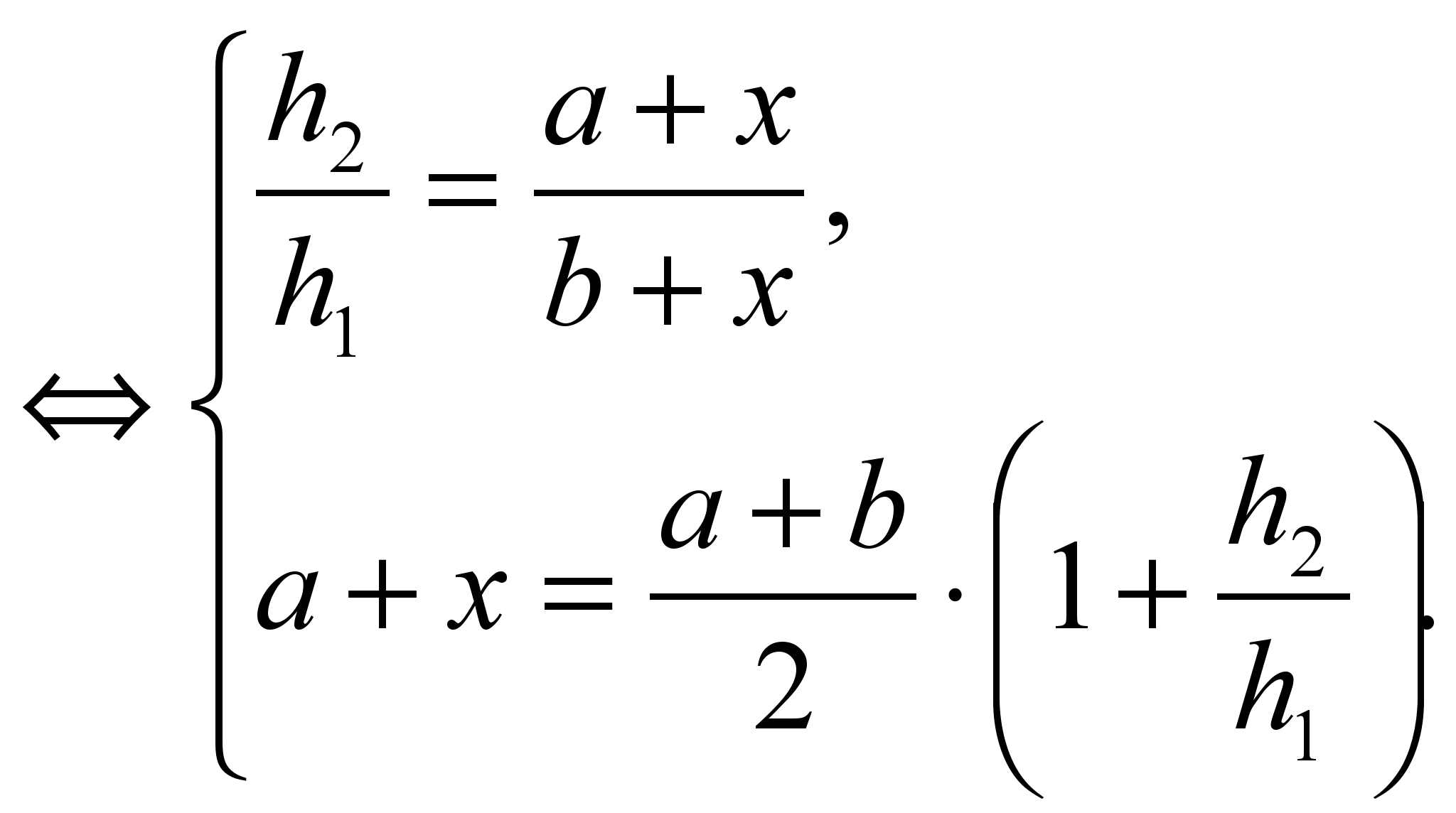
Sistemska rešitev 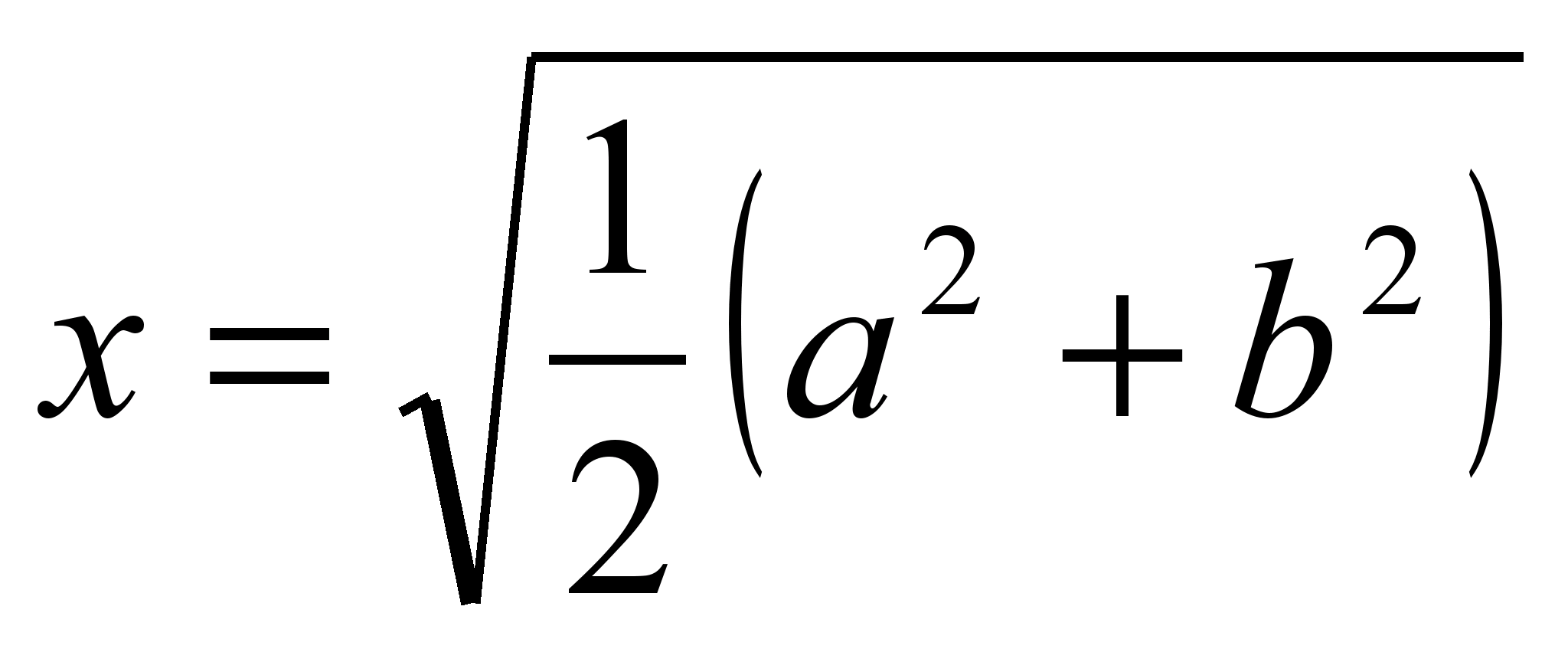 .
.
torej dolžina odseka, ki deli trapez na dva enaka, je enaka 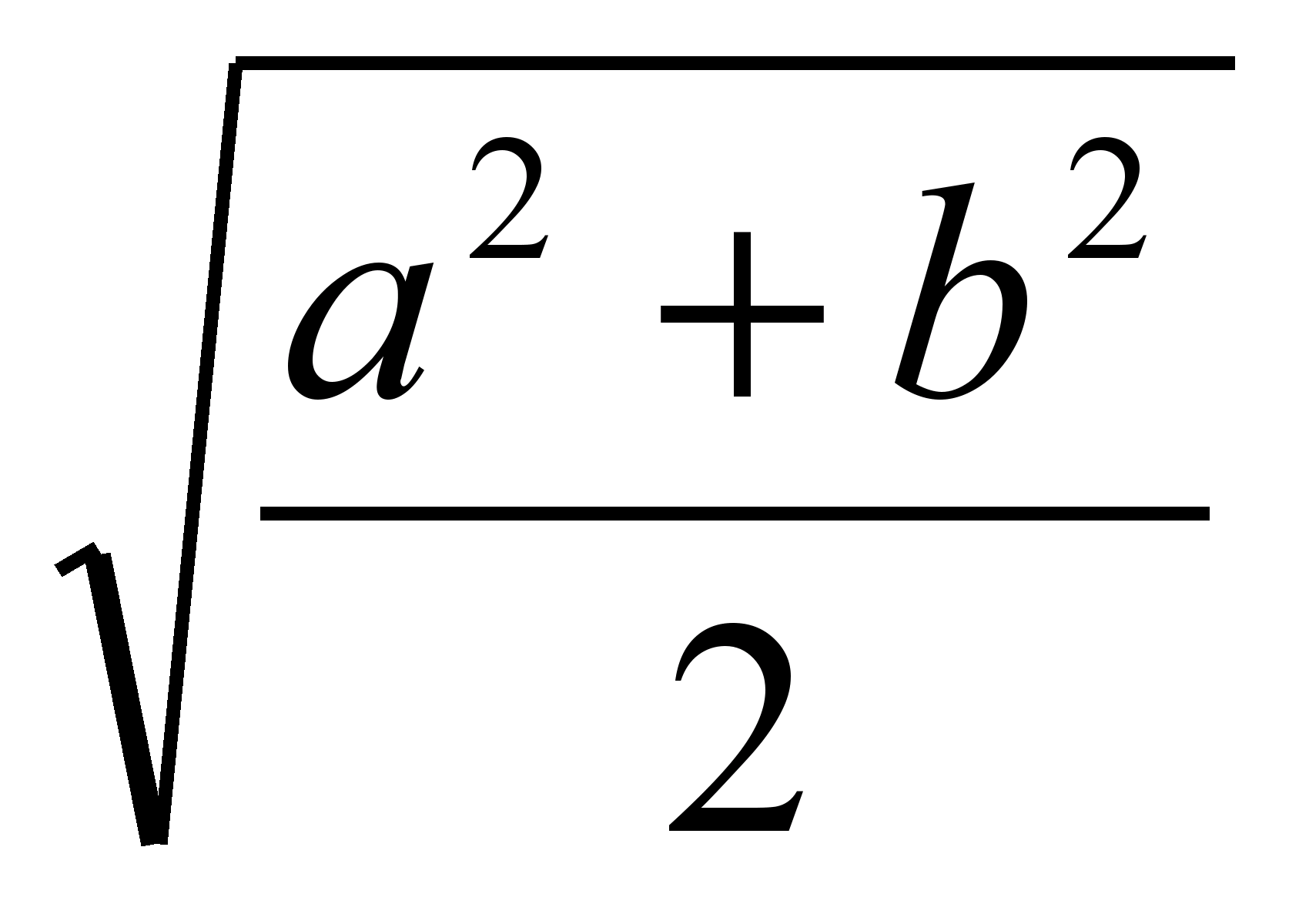 (srednje kvadratne dolžine baz).
).
(srednje kvadratne dolžine baz).
).
Seznam lekcij je zdaj enak kratkim povzetkom. V enakokrakem trapezu so osnovni koti skladni. Izrek 2. Če sta kota pri osnovici trapeza skladna, je trapez enakokrak. Rešene naloge V enakokrakem trapezu je osnovni kot 73°. Poišči vse druge kote trapeza. V enakokrakem trapezu je osnovni kot trikrat večji od notranjega kota na koncu krajše osnove. Poiščite vse kote trapeza.
V trapezu odsek, ki poteka iz sredine stranice vzporedno z osnovami, seka drugo stranico na njeni sredini. Poiščite dolžino trapeza na srednji črti. V trapezu je velika osnovka dolga 27 cm in je za 10 cm daljša od osnovke.
Da bi učenci spoznali povezavo med navedenimi segmenti, morajo biti pozvani, da jih zgradijo za dani trapez. Učenci bodo brez težav zgradili srednjo črto trapeza in odsek, ki poteka skozi presečišče diagonal trapeza vzporedno z osnovami. Kje bosta tretji in četrti segment? Odgovor na to vprašanje naj bi študente vodil do odkrivanja razmerja med povprečji.
Poiščite dolžine trapeznih osnov. V enakokrakem trapezu sta diagonali skladni. Naloga 2. Če sta diagonali v trapezu skladni, potem je trapez enakokrak. Naloga 3. Katera koli točka na srednji črti trapeza je enako oddaljena od dveh vzporednih premic, ki vsebujeta osnovici trapeza. Če je točka v ravnini enako oddaljena od dveh vzporednih premic, ki vsebujeta osnovici trapeza, potem točka pripada premici, ki vsebuje. trapez v srednji črti. Rešen problem. V trapezu je kateri koli odsek premice, ki povezuje točko na krajši osnovi s točko na večji osnovi, razpolovljen na središčnici trapeza.
Atribut in lastnost včrtanega in opisanega štirikotnika je treba določiti za vse učencem znane štirikotnike, vključno s trapezom.
Lastnosti opisanega trapeza. Trapez lahko opišemo krogu, če in samo če je vsota dolžin osnov enaka vsoti dolžin stranic.
Prvi je očiten. Za dokaz druge posledice je treba ugotoviti, da je kot COD direktno, kar tudi ni nič hudega. Toda poznavanje te posledice nam omogoča uporabo pravokotnega trikotnika pri reševanju problemov.
V trapezu se simetrali notranjih kotov na koncih stranske stranice sekata pod pravim kotom. V trapezu se simetrale notranjih kotov na koncih stranske stranice sekajo v točki, ki leži na srednji črti trapeza. Naloga 4. V enakokrakem trapezu je osnovni kot 60 °. Dokaži, da je krajša osnovna dolžina enaka razliki med daljšo osnovno dolžino in dolžino stranske stranice.
V enakokrakem trapezu je diagonala 10 cm in je z osnovo 60°. Poišči dolžino srednje dolgega trapeza. Osnovice trapeza so dolge 3 in 5 enot, ena diagonala je pravokotna na stranico, druga diagonala pa razpolovi kot. na večji podlagi. Poiščite višino trapeza. S pomočjo ravnila in šestila sestavi trapez z osnovama, ki se ujemajo z danima odsekoma, in straneh, skladen. dva druga podana segmenta.
Določimo posledice za enakokraki obrobni trapez :
|
|
višina enakokrakega okroglega enakokrakega trapeza je geometrična sredina osnov trapeza. Diagonale in koti trapezaS pomočjo ravnila in šestila sestavi trapez z osnovama, ki se ujemajo z danima odsekoma, in stranicami, ki sta skladni. na dva druga podana segmenta. Geometrija je poseben predmet matematike, ki se ukvarja z oblikami in predmeti ter z njimi povezanimi problemi. obstajati različni tipi geometrijske oblike. Nekaj pomembnih 2D oblik je kvadrat, pravokotnik, trikotnik, mnogokotnik, krog, paralelogram, trapez, romb itd. obliko, omejeno s štirimi stranicami, imenujemo štirikotnik. |
Razmislite o osnovnih načelih metodologije za preučevanje lastnosti trapeza.
Prvič, je uporaba pristop k nalogi . V teoretični tečaj geometrije ni treba uvajati novih lastnosti trapeza. Te lastnosti učenci odkrijejo in oblikujejo z reševanjem problemov (bolje kot problemski sistemi). Pomembno je, da učitelj ve, katere naloge naj si postavi in na kateri točki učnega procesa. Poleg tega je lahko vsaka lastnost ključna naloga v sistemu nalog.
Drugič, »spiralna« organizacija proučevanja lastnosti trapeza
. K posameznim lastnostim se lahko vrnete večkrat, takrat je verjetno, da si jih bodo učenci zapomnili. Na primer, lastnost štirih točk je mogoče dokazati s preučevanjem podobnosti in nato z uporabo vektorjev. Enako površino trikotnikov, ki mejijo na stranice trapeza, je mogoče dokazati z uporabo lastnosti trikotnikov, ki imajo enake višine, narisano na straneh, ki ležijo na eni ravni črti, in formula 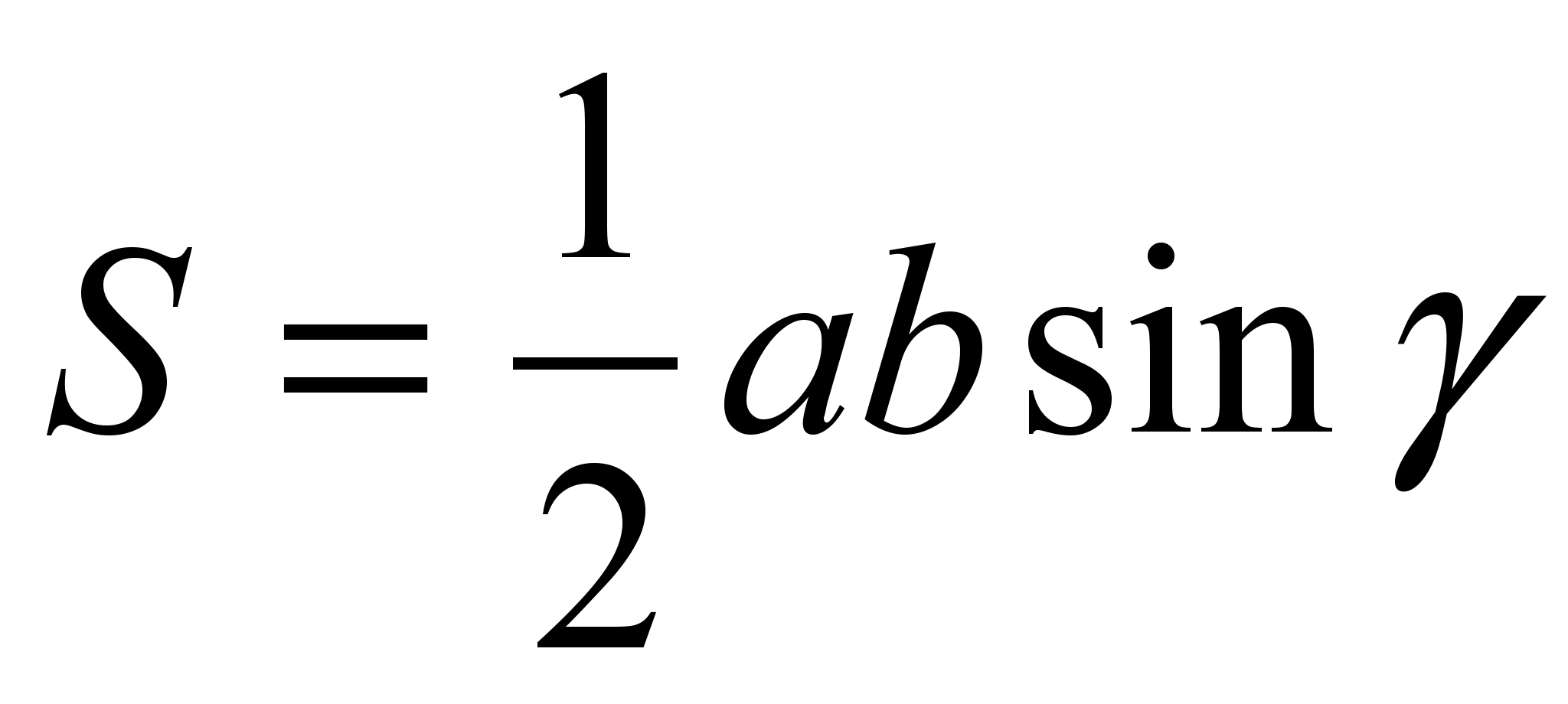 . Ugotovite lahko lastnosti pravokotnega trikotnika na opisanem trapezu, sinusni izrek na včrtanem trapezu in tako naprej.
. Ugotovite lahko lastnosti pravokotnega trikotnika na opisanem trapezu, sinusni izrek na včrtanem trapezu in tako naprej.
Predlagana vključitev "neprogramskih" lastnosti trapeza v vsebino šolskega predmeta geometrije, tehnologija nalog za njihovo preučevanje, ponavljajoče se sklicevanje na lastnosti trapeza pri preučevanju drugih tem bo študentom omogočilo globlje razumevanje trapeza in zagotoviti uspešnost reševanja problemov pri uporabi njegovih lastnosti.
Zato bomo poklicali enega od njih velik
, drugič - majhna osnova
trapez. Višina
trapez lahko imenujemo kateri koli odsek navpičnice, potegnjen iz oglišč na ustrezno nasprotno stran (za vsako oglišče sta dve nasprotni strani), zaprt med vzeto ogliščem in nasprotno stranjo. Lahko pa izpostavimo posebna vrsta"višine.
Opredelitev 8.
Višina osnove trapeza je odsek ravne črte, ki je pravokoten na osnovici, zaprt med osnovama.
Izrek 7
. Srednja črta trapeza je vzporedna z osnovama in je enaka polovici njihove vsote.
Dokaz. Podana naj bosta trapez ABCD in srednja črta KM. Skozi točki B in M nariši premico. Stranico AD nadaljujemo skozi točko D, dokler se ne preseka z BM. Trikotnika BCm in MPD sta enaka po stranicah in dveh kotih (CM=MD, ∠ BCM=∠ MDP - prekrivajoča se, ∠ BMC=∠ DMP - navpična), zato je VM=MP ali točka M razpolovišče BP. KM je srednjica v trikotniku ABP. Glede na lastnost srednje črte trikotnika je KM vzporedna z AP in še posebej z AD in je enaka polovici AP: 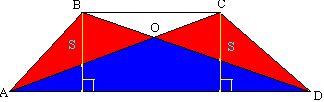 Izrek 8
. Diagonale delijo trapez na štiri dele, od katerih sta dva, ki mejita na stranice, enaka.
Izrek 8
. Diagonale delijo trapez na štiri dele, od katerih sta dva, ki mejita na stranice, enaka.
Naj vas spomnim, da se figure imenujejo enake, če imajo enako površino. Trikotnika ABD in ACD sta enaka: imata enaki višini (označeni z rumeno) in skupno osnovo. Ti trikotniki imajo skupni del AOD. Njihovo območje je mogoče razširiti na naslednji način: 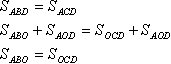
 Vrste trapeza:
Vrste trapeza:
Opredelitev 9.
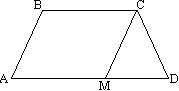
(Slika 1) Ostrokotni trapez je trapez, v katerem so koti, ki mejijo na večjo osnovo, ostri.
Opredelitev 10.
(Slika 2) Topi trapez je trapez, pri katerem je eden od kotov, ki mejijo na večjo osnovo, top.
Opredelitev 11.
(Slika 4) Trapez imenujemo pravokotnik, pri katerem je ena stranica pravokotna na osnove.
Opredelitev 12.
(Slika 3) Enakokraki (enakokraki, enakokraki) je trapez, pri katerem sta stranici enaki.
 Lastnosti enakokrakega trapeza:
Lastnosti enakokrakega trapeza:
Izrek 10
. Koti, ki ležijo na vsaki od osnov enakokrakega trapeza, so enaki.
Dokaz. Dokažimo na primer enakost kotov A in D z večjo osnovo AD enakokrakega trapeza ABCD. V ta namen narišemo premico skozi točko C vzporedno s stransko stranico AB. Veliko osnovo bo sekal v točki M. Štirikotnik ABCM je paralelogram, ker po zgradbi ima dva para vzporednih stranic. Zato je odsek CM sekanse, ki je zaprt znotraj trapeza, enak njegovi stranski stranici: CM=AB. Od tod je razvidno, da je CM=CD, trikotnik CMD je enakokrak, ∠CMD=∠CDM in torej ∠A=∠D. Tudi kota pri manjši osnovnici sta enaka, ker so za tiste, ki so notranje enostranske in imajo vsoto dveh črt. 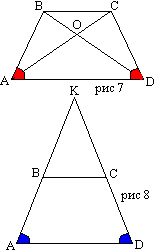 Izrek 11
. Diagonali enakokrakega trapeza sta enaki.
Izrek 11
. Diagonali enakokrakega trapeza sta enaki.
Dokaz. Razmislite o trikotnikih ABD in ACD. Enak je na dveh stranicah in kotu med njima (AB=CD, AD je skupen, kota A in D sta enaka po izreku 10). Zato je AC=BD.
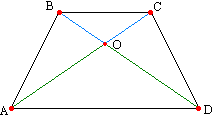 Izrek 13
. Diagonale enakokrakega trapeza so s presečiščem razdeljene na ustrezno enake odseke. Razmislite o trikotnikih ABD in ACD. Enak je na dveh stranicah in kotu med njima (AB=CD, AD je skupen, kota A in D sta enaka po izreku 10). Zato je ∠ ОАD=∠ ОDA, zato sta kota OВС in OSV enaka kot ustrezno prekrivajoča se kota ODA in OAD. Spomnimo se izreka: če sta dva kota v trikotniku enaka, potem je ta enakokrak, torej sta trikotnika ОВС in ОAD enakokraka, kar pomeni OS=OB in OA=OD itd.
Izrek 13
. Diagonale enakokrakega trapeza so s presečiščem razdeljene na ustrezno enake odseke. Razmislite o trikotnikih ABD in ACD. Enak je na dveh stranicah in kotu med njima (AB=CD, AD je skupen, kota A in D sta enaka po izreku 10). Zato je ∠ ОАD=∠ ОDA, zato sta kota OВС in OSV enaka kot ustrezno prekrivajoča se kota ODA in OAD. Spomnimo se izreka: če sta dva kota v trikotniku enaka, potem je ta enakokrak, torej sta trikotnika ОВС in ОAD enakokraka, kar pomeni OS=OB in OA=OD itd.
Enakokraki trapez je simetričen lik.
Opredelitev 13.
Simetrična os enakokrakega trapeza se imenuje ravna črta, ki poteka skozi središča njegovih baz.
Izrek 14
. Simetrijska os enakokrakega trapeza je pravokotna na njegove osnove. 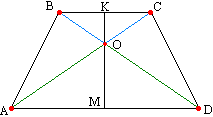 V izreku 9 smo dokazali, da premica, ki povezuje razpolovišči osnov trapeza, poteka skozi presečišče diagonal. Nato (izrek 13) smo dokazali, da sta trikotnika AOD in BOC enakokraka. OM in OK sta mediani teh trikotnikov po definiciji. Spomnimo se lastnosti enakokrakega trikotnika: mediana enakokrakega trikotnika, spuščena na osnovo, je tudi višina trikotnika. Zaradi pravokotnosti osnov delov premice KM je simetrijska os pravokotna na osnovke.
V izreku 9 smo dokazali, da premica, ki povezuje razpolovišči osnov trapeza, poteka skozi presečišče diagonal. Nato (izrek 13) smo dokazali, da sta trikotnika AOD in BOC enakokraka. OM in OK sta mediani teh trikotnikov po definiciji. Spomnimo se lastnosti enakokrakega trikotnika: mediana enakokrakega trikotnika, spuščena na osnovo, je tudi višina trikotnika. Zaradi pravokotnosti osnov delov premice KM je simetrijska os pravokotna na osnovke.
Znaki, ki razlikujejo enakokraki trapez med vsemi trapezi:
Izrek 15
. Če sta kota, ki mejita na eno od osnov trapeza, enaka, potem je trapez enakokrak.
Izrek 16
. Če sta diagonali trapeza enaki, potem je trapez enakokrak.
Izrek 17
. Če stranske stranice trapeza, razširjene do presečišča, tvorijo enakokrak trikotnik skupaj z njegovo veliko osnovo, potem je trapez enakokrak.
Izrek 18
. Če lahko trapez vpišemo v krog, potem je enakokrak.
Znak pravokotnega trapeza:
Izrek 19
. Vsak štirikotnik, ki ima samo dva prava kota v sosednjih ogliščih, je pravokotni trapez (očitno je, da sta stranici vzporedni, ker sta enostranici enaki. v primeru, ko so trije pravi koti pravokotnik)
Izrek 20
. Polmer kroga, včrtanega v trapez, je enak polovici višine osnove. 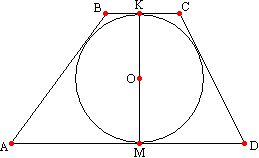 Dokaz tega izreka je pojasniti, da polmeri, narisani na osnovici, ležijo na višini trapeza. Iz točke O - središča kroga ABCD, včrtanega v ta trapez, narišemo polmere do stičnih točk z njegovimi osnovami trapeza. Kot veste, je polmer, narisan na stično točko, pravokoten na tangento, torej OK ^ BC in OM ^ AD. Spomnimo se izreka: če je premica pravokotna na eno od vzporednih premic, je pravokotna tudi na drugo. Zato je tudi premica OK pravokotna na AD. Tako potekata dve premici, pravokotni na premico AD, skozi točko O, kar pa ne more biti, zato ti premici sovpadata in sestavljata skupno navpičnico KM, ki je enaka vsoti dveh polmerov in je premer včrtane krožnice, torej r=KM/2 ali r=h/2.
Dokaz tega izreka je pojasniti, da polmeri, narisani na osnovici, ležijo na višini trapeza. Iz točke O - središča kroga ABCD, včrtanega v ta trapez, narišemo polmere do stičnih točk z njegovimi osnovami trapeza. Kot veste, je polmer, narisan na stično točko, pravokoten na tangento, torej OK ^ BC in OM ^ AD. Spomnimo se izreka: če je premica pravokotna na eno od vzporednih premic, je pravokotna tudi na drugo. Zato je tudi premica OK pravokotna na AD. Tako potekata dve premici, pravokotni na premico AD, skozi točko O, kar pa ne more biti, zato ti premici sovpadata in sestavljata skupno navpičnico KM, ki je enaka vsoti dveh polmerov in je premer včrtane krožnice, torej r=KM/2 ali r=h/2.
Izrek 21
. Ploščina trapeza je enaka produktu polovice vsote baz in višine baz. 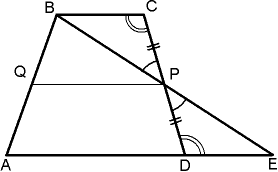
Dokaz: Naj bo ABCD dani trapez, AB in CD pa njegovi osnovici. Naj bo tudi AH višina, spuščena iz točke A na premico CD. Potem je S ABCD = S ACD + S ABC.
Toda S ACD = 1/2AH CD in S ABC = 1/2AH AB.
Zato je S ABCD = 1/2AH (AB + CD).
Q.E.D.
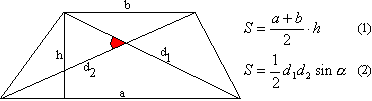 Druga formula se je preselila iz štirikotnika.
Druga formula se je preselila iz štirikotnika.
Morda bi bilo koristno prebrati:
- Od kod je Mihail Sergejevič Gorbačov?;
- Kako preživeti postne dneve za zdravje in hujšanje Kako si pravilno razporediti postne dneve;
- Pravilna prehrana za imuniteto Živila, ki krepijo človeški imunski sistem;
- Kdo je bil vodja Ingušetije pred Jevkurovim;
- Razcepljena osebnost - fikcija ali resnična bolezen?;
- Baby down - kaj to pomeni?;
- Dan svetih žena, ki nosijo miro;
- Pasijonosec Jevgenij Botkin Mučenik Jevgenij Botkin;
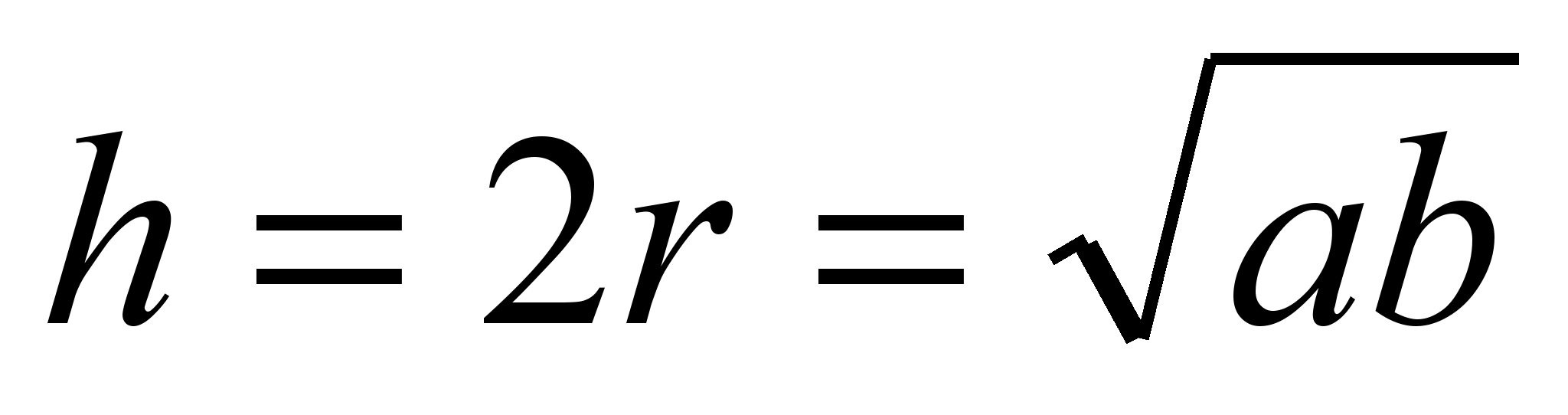 .
.