Cos ставлення. Прямокутний трикутник. Детальна теорія з прикладами
Інструкція
Спосіб 1. Використання теореми Піфагора. Теорема свідчить: квадрат гіпотенузи дорівнює сумі квадратів катетів. Звідси випливає, що будь-яку зі сторін прямокутного трикутника можна обчислити, знаючи дві інші сторони (рис.2).
Спосіб 2. Випливає з того, що медіана, проведена з прямого кутадо гіпотенузи, утворює між собою 3 подібні трикутники (рис. 3). На цьому малюнку подібними є трикутники ABC, BCD та ACD.
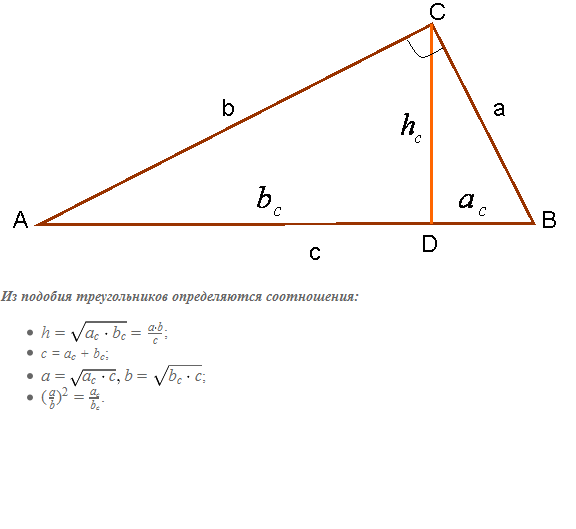
Гіпотенузою називається сторона у прямокутному трикутнику, яка знаходиться навпроти кута 90 градусів. Щоб розрахувати його довжину, достатньо знати довжину одного з катетів і величину одного з гострих кутів трикутника.

Інструкція
При відомому катете і гострому вугіллі прямокутного трикутника, то розмір гіпотенузи може дорівнювати відношенню катета до косінус/синус цього кута, якщо даний кут є йому протилежним/прилеглим:
h = C1(або C2)/sinα;
h = С1(або С2)/cosα.
Приклад: Нехай дано прямокутний трикутник ABC з гіпотенузою AB і прямим кутом C. Нехай кут B дорівнює 60 градусів, а кут A 30 градусів Довжина катета BC 8 см. Треба знайти довжину гіпотенузи AB. Для цього можна скористатися будь-яким із запропонованих вище способів:
AB = BC/cos60 = 8 см.
AB = BC/sin30 = 8 см.
Гіпотенузою називають сторону прямокутного трикутника, що лежить навпроти прямого кута. Вона є найбільшою стороною прямокутного трикутника. Розрахувати її можна з теоремі Піфагора чи з допомогою формул тригонометричних функцій.
![]()
Інструкція
Катетами називають сторони прямокутного трикутника, що належать до прямого кута. На малюнку катети позначені як AB та BC. Нехай задані довжини обох катетів. Позначимо їх як | AB | та |BC|. Щоб знайти довжину гіпотенузи |AC|, скористаємося теоремою Піфагора. Відповідно до цієї теоремі сума квадратів катетів дорівнює квадрату гіпотенузи, тобто. у позначеннях нашого малюнка |AB|^2 + |BC|^2 = |AC|^2. З формули отримуємо, що довжина гіпотенузи AC перебуває як |AC| = √(|AB|^2 + |BC|^2).
Розглянемо приклад. Нехай задані довжини катетів | AB | = 13, | BC | = 21. По теоремі Піфагора отримуємо, що |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610. Щоб отримати довжину гіпотенузи, необхідно витягти квадратний корінь із суми квадратів катетів, тобто. у складі 610: |AC| = √610. Скориставшись таблицею квадратів цілих чисел, з'ясовуємо, що число 610 перестав бути повним квадратом будь-якого цілого числа. Для того, щоб отримати остаточне значення довжини гіпотенузи, спробуємо винести повний квадрат під знак кореня. Для цього розкладемо число 610 на множники. 610 = 2 * 5 * 61. За таблицею простих чиселбачимо, що 61 – число просте. Тому подальше наведення числа √610 неможливе. Отримуємо остаточну відповідь | AC | = √610.
Якби квадрат гіпотенузи дорівнював, наприклад, 675, тоді √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. У разі, якщо подібне наведення можливе, виконуйте зворотну перевірку - зведіть результат у квадрат і порівняйте з вихідним значенням.
Нехай нам відомий один із катетів і прилеглий до нього кут. Для певності нехай це катет |AB| та кут α. Тоді ми можемо скористатися формулою для тригонометричної функції косинус – косинус кута дорівнює відношенню прилеглого катета до гіпотенузи. Тобто. у наших позначеннях cos α = | AB | / | AC |. Звідси отримуємо довжину гіпотенузи | AC | = | AB | / cos α.
Якщо нам відомі катет |BC| та кут α, то скористаємося формулою для обчислення синуса кута – синус кута дорівнює відношенню протилежного катета до гіпотенузи: sin α = |BC| / | AC |. Отримуємо, що довжина гіпотенузи як |AC| = | BC | / cos α.
Для наочності розглянемо приклад. Нехай дана довжина катета | AB | = 15. І кут α = 60 °. Отримуємо |AC| = 15 / cos 60 ° = 15 / 0.5 = 30.
Розглянемо як можна перевірити свій результат за допомогою теореми Піфагора. І тому необхідно порахувати довжину другого катета |BC|. Скориставшись формулою для тангенсу кута tg = |BC| / | AC |, отримуємо | BC | = | AB | * tg α = 15 * tg 60 ° = 15 * √3. Далі застосовуємо теорему Піфагора, отримуємо 15^2+(15*√3)^2=30^2=>225+675=900. Перевірка виконана.
Розрахувавши гіпотенузу, виконуйте перевірку – чи задовольняє отримане значення теоремі Піфагора.
Джерела:
- Таблиця простих чисел від 1 до 10 000
Катетаминазивають дві короткі сторони прямокутного трикутника, що становлять ту його вершину, величина якої дорівнює 90°. Третю сторону у такому трикутнику називають гіпотенузою. Всі ці сторони та кути трикутника пов'язані між собою певними співвідношеннями, які дозволяють обчислити довжину катета, якщо відомо кілька інших параметрів.

Інструкція
Використовуйте теорему Піфагора для обчислення довжини катета (A), якщо відома довжина двох інших сторін (B і C) прямокутного трикутника. Ця теорема стверджує, що сума зведених у квадрат довжин катетів дорівнює квадрату гіпотенузи. З цього випливає, що довжина кожного з катетів дорівнює квадратному кореню з різниці квадратів довжин гіпотенузи та другого катета: A=√(C²-B²).
Скористайтеся визначенням прямої тригонометричної функції «синус» для гострого кута, якщо відома величина кута (α), що лежить навпроти катета, що обчислюється, і довжина гіпотенузи (C). Це визначення стверджує, що синус цього відомого кутадорівнює відношенню довжини шуканого катета до довжини гіпотенузи. Це означає, що довжина катета, що шукається, дорівнює добутку довжини гіпотенузи на синус відомого кута: A=C∗sin(α). Для цих відомих величин можна використовувати і визначення функції косеканс і розрахувати потрібну довжину, розділивши довжину гіпотенузи на косеканс відомого кута A=C/cosec(α).
Визначте пряму тригонометричну функцію косинус, якщо крім довжини гіпотенузи (C) відома і величина гострого кута (β), прилеглого до шуканого катету. Косинус цього кута визначається як співвідношення довжин шуканого катета і гіпотенузи, та якщо з цього можна дійти невтішного висновку, що довжина катета дорівнює добутку довжини гіпотенузи на косинус відомого кута: A=C∗cos(β). Можна скористатися визначенням функції секанс та обчислити потрібне значення, розділивши довжину гіпотенузи на секанс відомого кута A=C/sec(β).
Виведіть потрібну формулу з аналогічного визначення для похідної тригонометричної функції тангенс, якщо крім величини гострого кута (α), що лежить навпроти катета (A), що шукається, відома довжина другого катета (B). Тангенсом протилежного шуканому катету кута називають відношення довжини цього катета до довжини другого катета. Отже, шукана величина дорівнюватиме добутку довжини відомого катета на тангенс відомого кута: A=B∗tg(α). З цих відомих величин можна вивести й іншу формулу, якщо скористатися визначенням функції котангенс. У цьому випадку для обчислення довжини катета треба буде знайти співвідношення довжини відомого катета до котангенсу відомого кута: A=B/ctg(α).
Відео на тему
Слово «катет» прийшло в російську мову з грецької. У точному перекладі воно означає виска, тобто перпендикуляр до землі. У математиці катетами називаються сторони, що утворюють прямий кут прямокутного трикутника. Протилежна цьому кутку сторона називається гіпотенузою. Термін «катет» застосовується також в архітектурі та технології зварювальних робіт.

Накресліть прямокутний трикутник АСВ. Позначте його катети як і b, а гіпотенузу - як. Усі сторони та кути прямокутного трикутника пов'язані між собою певними відносинами. Відношення катета, що протилежить одному з гострих кутів, до гіпотенузи називається синусом даного кута. У цьому трикутнику sinCAB=a/c. Косинус - це ставлення до гіпотенузи катета, що прилягає, тобто cosCAB=b/c. Зворотні відносини називаються секансом та косекансом.
Секанс даного кута виходить при розподілі гіпотенузи на катет, тобто secCAB=c/b. Виходить величина, зворотна косинус, тобто виразити її можна за формулою secCAB=1/cosSAB.
Косеканс дорівнює частці від поділу гіпотенузи на протилежний катет і це величина, зворотна синусу. Вона може бути розрахована за формулою cosecCAB=1/sinCAB
Обидва катета пов'язані між собою тангенсом та котангенсом. У даному випадкутангенсом буде відношення сторони a до сторони b, тобто катета протилежного до прилеглого. Це відношення може бути виражене формулою tgCAB=a/b. Відповідно, зворотним ставленням буде котангенс: ctgCAB=b/a.
Співвідношення між розмірами гіпотенузи та обох катетів визначив ще давньогрецький математик Піфагор. Теоремою, названою його ім'ям, люди користуються досі. Вона свідчить, що квадрат гіпотенузи дорівнює сумі квадратів катетів, тобто с2 = a2 + b2. Відповідно, кожен катет дорівнюватиме квадратному кореню з різниці квадратів гіпотенузи та іншого катета. Цю формулу можна записати як b = √ (с2-а2).
Довжину катета можна виразити і через відомі вам співвідношення. Згідно з теоремами синусів і косінусів, катет дорівнює добутку гіпотенузи на одну з цих функцій. Можна його виразити через тангенс або котангенс. Катету можна знайти, наприклад, за формулою a = b*tan CAB. Точно так само, залежно від заданих тангенсу або котангенсу, визначається і другий катет.
В архітектурі також використовується термін "катет". Він застосовується по відношенню до іонічної капітелі і позначає виска через середину її задка. Тобто і в цьому випадку цим терміном позначається перпендикуляр заданої лінії.
У технології зварювальних робіт є поняття «катет кутового шва». Як і в інших випадках, це найкоротша відстань. Тут мова йдепро проміжок між однією з деталей, що зварюються, до межі шва, що знаходиться на поверхні іншої деталі.
Відео на тему
Джерела:
- що таке катет та гіпотенуза
Відео на тему
Зверніть увагу
При розрахунку сторін прямокутного трикутника може зіграти знання його ознак:
1) Якщо катет прямого кута лежить навпроти кута 30 градусів, він дорівнює половині гіпотенузи;
2) Гіпотенуза завжди довша за будь-який з катетів;
3) Якщо навколо прямокутного трикутника описано коло, то його центр має лежати в середині гіпотенузи.
Тригонометрія є розділом математики, що вивчає тригонометричні функції, а також їх використання на практиці. До таких функцій відносяться синус, косинус, тангенс та котангенс.
Синус – це тригонометрична функція , Відношення величини протилежного катета до величини гіпотенузи
Синус у тригонометрії.
Як уже сказано вище, синус має безпосереднє відношення до тригонометрії та тригонометричних функцій. Його функція визначається тим, щоб
- допомагати розрахувати кут, за умови популярності величин сторін трикутника;
- допомагати вирахувати величини сторони трикутника, за умови популярності кута.
Необхідно пам'ятати, що величина синуса завжди однакова для будь-яких розмірів трикутника, оскільки синус – це не вимір, а співвідношення.
Отже, щоб не вираховувати цю постійну величину при кожному вирішенні тієї чи іншої завдання, були створені спеціальні тригонометричні таблиці. Вони величини синусів, косінусів, тангенсів і котангенсів вже прораховані і закріплені. Зазвичай ці таблиці наводяться на форзаці підручників з алгебри та геометрії. Також їх можна знайти в Інтернеті.
Синус у геометрії.
Геометрія вимагає наочності, тому, щоб зрозуміти на практиці, що таке синус кутапотрібно намалювати трикутник з прямим кутом.
Припустимо, що сторони, що утворюють прямий кут, названі а, в,протилежний їм кут – х.
Зазвичай у завданнях вказано довжину сторін. Припустимо, а = 3, = 4. У такому разі співвідношення сторін виглядатиме як ¾. При цьому якщо подовжити сторони трикутника, що прилягають до гострого кута х, то збільшаться і сторони аі ві гіпотенуза – третя сторона прямокутного трикутника, що лежить не під прямим кутом до основи. Тепер сторони трикутника можна назвати інакше, скажімо: m, n, k.
У цьому видозміні спрацював закон тригонометрії: довжини сторін трикутника змінилися, які ставлення – немає.
Той факт, що при зміні довжини сторін трикутника у скільки завгодно разів і при збереженні величини кута х, співвідношення між його сторонами все одно залишиться незмінним, помітили ще давні вчені. У нашому випадку довжина сторін могла змінитися так: а/в = ¾, при подовженні сторони адо 6 см, а в- До 8 см отримуємо: m/n = 6/8 = 3/4.
Співвідношення сторін у прямокутному трикутнику у зв'язку з цим отримали назви:
- синус кута х - це відношення протилежного катета до гіпотенузи: sinx = а / с;
- косинус кута х – це відношення прилеглого катета до гіпотенузи: сosx = в/с;
- тангенс кута х – це відношення протилежного катета до прилеглого: tgx = а/в;
- котангенс кута х – це відношення прилеглого катета до протилежного: ctgx = в/а.
Вивчення тригонометрії ми розпочнемо з прямокутного трикутника. Визначимо, що таке синус та косинус, а також тангенс та котангенс гострого кута. Це є основи тригонометрії.
Нагадаємо, що прямий кут- Це кут, рівний. Іншими словами, половина розгорнутого кута.
Гострий кут- менший.
Тупий кут- Більший. Стосовно такого кута «тупий» - не образа, а математичний термін:-)

Намалюємо прямокутний трикутник. Прямий кут зазвичай позначається. Звернімо увагу, що сторона, що лежить навпроти кута, позначається тією ж літерою, лише маленькою. Так, сторона, що лежить навпроти кута, позначається.
Кут позначається відповідною грецькою літерою.
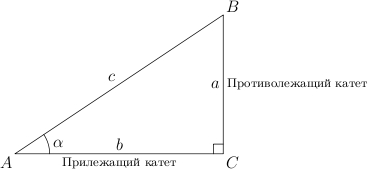
Гіпотенузапрямокутного трикутника - це сторона, що лежить навпроти прямого кута.
Катети- Сторони, що лежать навпроти гострих кутів.
Катет, що лежить навпроти кута, називається протилежним(По відношенню до кута). Інший катет, який лежить на одній із сторін кута, називається прилеглим.
Сінусгострого кута в прямокутному трикутнику - це відношення протилежного катета до гіпотенузи:
Косінусгострого кута у прямокутному трикутнику - відношення прилеглого катета до гіпотенузи:
Тангенсгострого кута в прямокутному трикутнику - відношення протилежного катета до прилеглого:
Інше (рівносильне) визначення: тангенсом гострого кута називається відношення синуса кута до його косинусу:
![]()
Котангенсгострого кута в прямокутному трикутнику - відношення прилеглого катета до протилежного (або, що те саме, відношення косинуса до синуса):
![]()
Зверніть увагу на основні співвідношення для синуса, косинуса, тангенсу та котангенсу, які наведені нижче. Вони стануть у нагоді нам при вирішенні завдань.
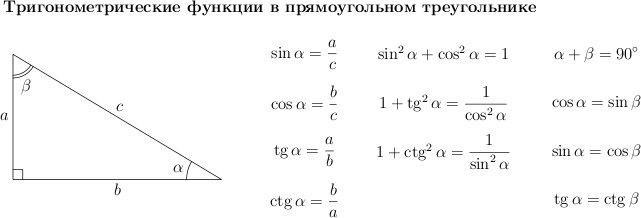
Давайте доведемо деякі з них.
1. Сума кутів будь-якого трикутника дорівнює. Значить, сума двох гострих кутів прямокутного трикутника дорівнює .
2. З одного боку, як ставлення протилежного катета до гіпотенузи. З іншого боку, оскільки для кута катет буде прилеглим.
Отримуємо, що ![]() . Іншими словами, .
. Іншими словами, .
3. Візьмемо теорему Піфагора: ![]() . Поділимо обидві частини на:
. Поділимо обидві частини на:
![]()
Ми отримали основне тригонометричне тотожність:
Таким чином, знаючи синус кута, ми можемо знайти його косинус, і навпаки.
4. Поділивши обидві частини основного тригонометричного тотожності на , отримаємо:
![]()
Це означає, що якщо нам дано тангенс гострого кута, ми відразу можемо знайти його косинус.
Аналогічно,
![]()
Добре, ми дали визначення та записали формули. А навіщо потрібні синус, косинус, тангенс і котангенс?
Ми знаємо, що сума кутів будь-якого трикутника дорівнює.
Знаємо співвідношення між сторонамипрямокутний трикутник. Це теорема Піфагора: ![]() .
.
Виходить, що знаючи два кути в трикутнику можна знайти третій. Знаючи дві сторони прямокутного трикутника, можна знайти третю. Значить, для кутів – своє співвідношення, для сторін – своє. А що робити, якщо у прямокутному трикутнику відомий один кут (крім прямого) та одна сторона, а знайти треба інші сторони?
Спочатку синус і косинус виникли через необхідність розраховувати величини прямокутних трикутниках. Було помічено, що й значення градусної міри кутів у прямокутному трикутнику не змінювати, то співвідношення сторін, хоч би ці сторони змінювалися у довжині, залишається завжди однаковим.Саме так і було введено поняття синуса та косинуса. Синус гострого кута у прямокутному трикутнику – це відношення протилежного катета до гіпотенузи, а косинус – прилеглого до гіпотенузи.
Теореми косінусів та синусів
Але косинуси та синуси можуть застосовуватися не тільки у прямокутних трикутниках. Щоб знайти значення тупого чи гострого кута, сторони будь-якого трикутника, достатньо застосувати теорему косінусів та синусів.Теорема косінусів досить проста: «Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін за вирахуванням подвоєного твору цих сторін на косинус кута між ними».
Існує два трактування теореми синусів: мала та розширена. Відповідно до малої: «У трикутнику кути пропорційні протилежним сторонам». Цю теорему часто розширюють за рахунок властивості описаного у трикутника кола: «У трикутнику кути пропорційні протилежним сторонам, а їх відношення дорівнює діаметру описаного кола».
Похідні
Похідна – математичний інструмент, що показує, як швидко змінюється функція щодо зміни її аргументу. Похідні використовуються в алгебрі, геометрії, економіці та фізиці, ряді технічних дисциплін.При вирішенні завдань потрібно знати табличні значення похідних тригонометричних функцій: синуса та косинуса. Похідною синуса є косинус, а косинуса – синус, але зі знаком «мінус».
Застосування в математиці
Особливо часто синуси та косинуси використовуються при вирішенні прямокутних трикутників та завдань, пов'язаних з ними.Зручність синусів і косінусів знайшло своє відображення і в техніці. Кути та сторони було просто оцінювати за теоремами косинусів та синусів, розбиваючи складні фігури та об'єкти на «прості» трикутники. Інженери та архітектори, які часто мають справу з розрахунками співвідношення сторін і градусних заходів, витрачали чимало часу та зусиль для обчислення косінусів та синусів не табличних кутів.
Тоді «на допомогу» прийшли таблиці Брадіса, що містять тисячі значень синусів, косінусів, тангенсів та котангенсів різних кутів. У радянський часдеякі викладачі змушували своїх підопічних вивчати сторінки таблиць Брадіса напам'ять.
На прямокутному трикутнику, як найпростішому з багатокутників, різні вчені мужі відточували свої знання в галузі тригонометрії ще в ті часи, коли цю галузь математики ніхто навіть не називав таким словом. Тому вказати автора, який виявив закономірності у співвідношеннях довжин сторін і величин кутів у цій плоскій геометричній фігурі, сьогодні неможливо. Такі співвідношення названі тригонометричними функціями і поділені на кілька груп, основною з яких умовно вважаються «прямі» функції. До цієї групи віднесено лише дві функції і одна з них – синус.
Інструкція
За визначенням у прямокутному трикутнику один з кутів дорівнює 90°, а через те, що сума його кутів у евклідовій геометрії має дорівнювати 180°, два інших кута є гострими (тобто. менше 90°). Закономірності співвідношень саме цих кутів і довжин сторін описують тригонометричні функції.
Функція, яка називається синусом гострого кута, визначає співвідношення між довжиною двох сторін прямокутного трикутника, одна з яких лежить навпроти цього гострого кута, а інша примикає до нього і лежить навпроти прямого кута. Так як сторона, що лежить навпроти прямого кута в такому трикутнику, називається гіпотенузою, а дві інші - катетами, визначення функції синус можна сформулювати як співвідношення між довжинами протилежного катета і гіпотенузи.
Крім такого найпростішого визначення цієї тригонометричної функції сьогодні існують і складніші: через коло в декартових координатах, через ряди, через рішення диференціальних та функціональних рівнянь. Ця функція безперервна, тобто її аргументами («областю визначень») може бути будь-яке число - від нескінченно негативного до нескінченно позитивного. А максимум і мінімум значень цієї функції обмежені діапазоном від -1 до +1 – це область її значень. Мінімальне значення синус приймає при куті 270°, що відповідає 3/2 числа Пі, а максимальне виходить при 90° (½ від Пі). Нульовими значення функції стають при 0 °, 180 °, 360 ° і т.д. З усього цього випливає, що синус є періодичною функцією і період її дорівнює 360° або подвоєному числу Пі.
Для практичних розрахунків значень цієї функції від заданого аргументу можна використовувати калькулятор - абсолютна більшість із них (включаючи програмний калькулятор, вбудований у операційну системукомп'ютера) має відповідну опцію.
Відео на тему
Інструкція
кутау прямокутному трикутнику, необхідно скористатися визначенням косинуса та знайти відношення прилеглого катета до гіпотенузи:
cos? = a/c, де а - Довжина катета, С - Довжина гіпотенузи.
Якщо потрібно знайти косинус кутау довільному трикутнику, необхідно скористатися теоремою косінусів:
якщо кут гострий: cos? = (a2 + b2 - c2) / (2ab);
якщо кут тупий: cos? = (с2 - a2 - b2) / (2ab), де а, b - Довжини сторін прилеглих до кута, С - Довжина сторони протилежної куту.
Якщо потрібно знайти косинус кутау довільній геометричній фігурі необхідно визначити величину кутау градусах чи радіанах, а косинус кутазнайти за його величиною за допомогою інженерного калькулятора, таблиць Брадіса або будь-якої іншої математичної програми.
Косінус- це базова тригонометрична функція кута. Вміння визначати косинус стане в нагоді у векторній алгебрі при визначенні проекцій векторів на різні осі.
Інструкція
соs?=(b?+c?-а?)/(2*b*c)
Є трикутник із сторонами а, b, с, рівними 3, 4, 5 мм, відповідно.
Знайти косинускута, укладеного між великими сторонами.
Позначимо протилежний стороні а кут через?, тоді, згідно з виведеною вище формулою, маємо:
соs?=(b?+c?-а?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 = 32/40 = 0,8
Відповідь: 0,8.
Якщо трикутник прямокутний, то знаходження косинуса кута достатньо знати довжини всього двох будь-яких сторін ( косинуспрямого кута дорівнює 0).
Нехай є прямокутний трикутник зі сторонами а, b, с, де - гіпотенуза.
Розглянемо всі варіанти:
Знайти соs?, якщо відомі довжини сторін а та b (катети трикутника)
Скористаємося додатково теоремою Піфагора:
соs?=(b?+c?-а?)/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?)) =(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)
Щоб перевірити правильність отриманої формули, підставимо у ній значення прикладу 1, тобто.
Зробивши елементарні обчислення, отримуємо:
Аналогічно перебуває косинусу прямокутному трикутникув інших випадках:
Відомі а і с (гіпотенуза та протилежний катет), знайти соs?
соs?=(b?+c?-а?)/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?)) =(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
Підставляючи значення а=3 та с=5 з першого прикладу, отримуємо:
Відомі b і с (гіпотенуза та прилеглий катет).
Знайти соs?
Провівши аналогічні (показані в прикладах 2 і 3 перетворення), отримаємо, що в цьому випадку косинусв трикутникуобчислюється за дуже простою формулою:
Простота виведеної формули пояснюється просто: фактично, що належить до кута? катет є проекцією гіпотенузи, тому його довжина дорівнює довжині гіпотенузи, помноженої на со?.
Підставляючи значення b=4 та с=5 з першого прикладу, отримаємо:
Отже, всі наші формули є вірними.
Порада 5: Як знайти гострий кут у прямокутному трикутнику
Прямо вугільнийтрикутник, ймовірно, - одна з найвідоміших, з історичної точки зору, геометричних фігур. Піфагоровим "штанам" конкуренцію може скласти лише "Евріка!" Архімед.

Вам знадобиться
- - креслення трикутника;
- - Лінійка;
- - Транспортир.
Інструкція
Сума кутів трикутника складає 180 градусів. У прямокутному трикутникуодин кут (прямий) завжди буде 90 градусів, інші гострими, тобто. менше 90 градусів кожен. Щоб визначити, який кут у прямокутному трикутникує прямим, виміряйте за допомогою лінійки сторони трикутника та визначте найбільшу. Вона називається гіпотенуза (AB) і знаходиться навпроти прямого кута (C). Інші дві сторони утворюють прямий кут і називаються катетами (AC, BC).
Коли визначили, який кут є гострим, ви можете виміряти величину кута за допомогою транспортира, або розрахувати за допомогою математичних формул.
Щоб визначити величину кута за допомогою транспортира, поєднайте його вершину (позначимо її літерою А) зі спеціальною позначкою на лінійці в центрі транспортира, катет АС повинен збігатися з верхнім краєм. Позначте на півкруглій частині транспортира точку, якою проходить гіпотенуза AB. Значення у цій точці відповідає величині кута в градусах. Якщо на транспортирі вказано 2 величини, то для гострого кута потрібно вибирати меншу, для тупого – більшу.
Отримане значення знайдіть у довідкових таблицях Брадіса та визначте якому куту відповідає отримане числове значення. Цим методом користувалися наші бабусі.
У наш час достатньо взяти калькулятор із функцією обчислення тригонометричних формул. Наприклад, вбудований калькулятор Windows. Запустіть програму "Калькулятор", у пункті меню "Вид" виберіть пункт "Інженерний". Обчисліть синус кута, що шукається, наприклад, sin (A) = BC/AB = 2/4 = 0.5
Переключіть калькулятор у режим зворотних функцій, клацнувши по кнопці INV на табло калькулятора, потім клацніть по кнопці розрахунку функції арксинуса (на табло позначено, як sin мінус першого ступеня). У вікні розрахунку з'явиться такий напис: asind (0.5) = 30. Тобто. значення шуканого кута – 30 градусів.
Джерела:
- Таблиці Брадіса (синуси, косинуси)
Теорема косінусів у математиці найчастіше використовується у тому випадку, коли необхідно знайти третю сторону по кутку та двом сторонам. Однак іноді умова завдання поставлена навпаки: потрібно знайти кут при заданих трьох сторонах.

Інструкція
Уявіть, що дано трикутник, у якого відомі довжини двох сторін і значення одного кута. Усі кути цього трикутника не рівні один одному, яке сторони також є різними за величиною. Кут γ лежить навпроти сторони трикутника, позначеної як AB, яка є основою цієї фігури. Через даний кут, а також через сторони AC і BC, що залишилися, можна знайти ту сторону трикутника, яка невідома, за теоремою косінусів, вивівши на її основі подану нижче формулу:
a^2=b^2+c^2-2bc*cosγ, де a=BC, b=AB, c=AC
Теорему косінусів інакше називають узагальненою теоремою Піфагора.
Можливо, буде корисно почитати:
- Як повернути коханого чоловіка без спілкування - перевірені змови сильних відунів Як повернути людину до себе;
- Сколеціфобія та боротьба з нею;
- Експерти висловилися за продовження роботи МКС;
- Будова та життєдіяльність інфузорій на прикладі інфузорії-туфельки;
- Архієпископ Іонафан (Єлецьких): Біля витоків народження Української Православної Церкви;
- Влада курганської області не платить регіональний маткапітал Губернатор Осипов виконує федеральні установки на прозорість виборів;
- Салат з пекінською капустою та крабовими паличками Салат пекінською капустою кукурудзою крабовими;
- Лукума - опис фрукту та його властивостей з фото Застосування в кулінарії;