Die Zufallsvariable x wird durch die Wahrscangegeben. Beispiele zur Lösung von Problemen zum Thema „Zufallsvariablen“

Übung 1. Die Verteilungsdichte einer kontinuierlichen Zufallsvariablen X hat die Form:
Finden:
a) Parameter A;
b) Verteilungsfunktion F(x) ;
c) die Wahrscheinlichkeit, dass eine Zufallsvariable X in das Intervall fällt;
d) mathematischer Erwartungswert MX und Varianz DX.
Zeichnen Sie einen Graphen der Funktionen f(x) und F(x).

Aufgabe 2. Finden Sie die Varianz der durch die Integralfunktion gegebenen Zufallsvariablen X.

Aufgabe 3. Finden Sie den mathematischen Erwartungswert der Zufallsvariablen X bei gegebener Verteilungsfunktion.

Aufgabe 4. Die Wahrscheinlichkeitsdichte einer Zufallsvariablen ist wie folgt gegeben: f(x) = A/x 4 (x = 1; +∞)
Finden Sie den Koeffizienten A, die Verteilungsfunktion F(x), den mathematischen Erwartungswert und die Varianz sowie die Wahrscheinlichkeit, dass die Zufallsvariable einen Wert im Intervall annimmt. Zeichnen Sie die Graphen f(x) und F(x).

Aufgabe. Die Verteilungsfunktion einer kontinuierlichen Zufallsvariablen ist wie folgt angegeben:

Bestimmen Sie die Parameter a und b, finden Sie einen Ausdruck für die Wahrscheinlichkeitsdichte f(x), den mathematischen Erwartungswert und die Varianz sowie die Wahrscheinlichkeit, dass die Zufallsvariable einen Wert im Intervall annimmt. Zeichnen Sie Graphen von f(x) und F(x).

Finden wir die Verteilungsdichtefunktion als Ableitung der Verteilungsfunktion.
F′=f(x)=a
Da wir wissen, dass wir den Parameter a finden werden:

oder 3a=1, woraus a = 1/3
Wir finden den Parameter b aus den folgenden Eigenschaften:
F(4) = a*4 + b = 1
1/3*4 + b = 1, woraus b = -1/3
Daher hat die Verteilungsfunktion die Form: F(x) = (x-1)/3

Erwarteter Wert.


Streuung.

1 / 9 4 3 - (1 / 9 1 3) - (5 / 2) 2 = 3 / 4
Lassen Sie uns die Wahrscheinlichkeit ermitteln, dass die Zufallsvariable einen Wert im Intervall annimmt
P(2< x< 3) = F(3) – F(2) = (1/3*3 - 1/3) - (1/3*2 - 1/3) = 1/3

Beispiel Nr. 1. Gegeben ist die Wahrf(x) einer kontinuierlichen Zufallsvariablen X. Erforderlich:

  1. Bestimmen Sie den Koeffizienten A.
  2. Finden Sie die Verteilungsfunktion F(x) .
  3. Konstruieren Sie schematisch Diagramme von F(x) und f(x).
  4. Finden Sie den mathematischen Erwartungswert und die Varianz von X.
  5. Finden Sie die Wahrscheinlichkeit, dass X einen Wert aus dem Intervall (2;3) annimmt.
f(x) = A*sqrt(x), 1 ≤ x ≤ 4.
Lösung:

Die Zufallsvariable X wird durch die Verteilungsdichte f(x) spezifiziert:


Suchen wir den Parameter A aus der Bedingung:



oder
14/3*A-1 = 0
Wo,
A = 3 / 14


Die Verteilungsfunktion kann mithilfe der Formel ermittelt werden.

Zufällige Variable Dabei handelt es sich um eine Größe, die als Ergebnis von Versuchen, die unter gleichen Bedingungen durchgeführt wurden, in Abhängigkeit von unberücksichtigten Zufallsfaktoren unterschiedliche, allgemein gesprochene Werte annimmt. Beispiele für Zufallsvariablen: die Anzahl der gewürfelten Punkte, die Anzahl fehlerhafter Produkte in einer Charge, die Abweichung des Auftreffpunkts eines Projektils vom Ziel, die Betriebszeit eines Geräts usw. Es gibt diskrete und kontinuierliche Variablen zufällige Variablen. Diskret Man nennt eine Zufallsvariable, deren mögliche Werte eine abzählbare Menge bilden, endlich oder unendlich (also eine Menge, deren Elemente nummeriert werden können).

Kontinuierlich Man nennt eine Zufallsvariable, deren mögliche Werte kontinuierlich ein endliches oder unendliches Intervall der Zahlengeraden ausfüllen. Die Anzahl der Werte einer kontinuierlichen Zufallsvariablen ist immer unendlich.

Wir bezeichnen Zufallsvariablen mit Großbuchstaben vom Ende des lateinischen Alphabets: X, Y, ...; Zufallsvariablenwerte – in Kleinbuchstaben: X, y,... . Auf diese Weise, X Bezeichnet die gesamte Menge möglicher Werte einer Zufallsvariablen und X - Einige seiner spezifischen Bedeutung.

Verteilungsgesetz Eine diskrete Zufallsvariable ist eine in beliebiger Form angegebene Entsprechung zwischen den möglichen Werten einer Zufallsvariablen und ihren Wahrscheinlichkeiten.

Lassen Sie die möglichen Werte der Zufallsvariablen X Sind . Als Ergebnis des Tests nimmt die Zufallsvariable einen dieser Werte an, d. h. Ein Ereignis aus einer vollständigen Gruppe paarweise inkompatibler Ereignisse wird auftreten.

Auch die Wahrscheinlichkeiten dieser Ereignisse seien bekannt:

Verteilungsgesetz einer Zufallsvariablen X Kann in Form einer Tabelle namens geschrieben werden Nahe Verbreitung Diskrete Zufallsvariable:

Für die Verteilungsreihe gilt Gleichheit (Normalisierungsbedingung).

Beispiel 3.1. Finden Sie das Verteilungsgesetz einer diskreten Zufallsvariablen X – die Häufigkeit, mit der bei zwei Münzwürfen „Kopf“ erscheint.

Die Verteilungsfunktion ist eine universelle Form zur Angabe des Verteilungsgesetzes sowohl diskreter als auch kontinuierlicher Zufallsvariablen.

Verteilungsfunktion einer ZufallsvariablenX Die Funktion wird aufgerufen F(X), Auf dem gesamten Zahlenstrahl wie folgt definiert:

F(X)= P(X< х ),

Das ist F(X) Es besteht eine Wahrscheinlichkeit, dass die Zufallsvariable X Wird einen Wert kleiner als annehmen X.

Die Verteilungsfunktion kann grafisch dargestellt werden. Für eine diskrete Zufallsvariable hat der Graph eine Stufenform. Konstruieren wir zum Beispiel einen Graphen der Verteilungsfunktion einer Zufallsvariablen, die durch die folgende Reihe gegeben ist (Abb. 3.1):

Reis. 3.1. Diagramm der Verteilungsfunktion einer diskreten Zufallsvariablen

Funktionssprünge treten an Punkten auf, die möglichen Werten der Zufallsvariablen entsprechen, und sind gleich den Wahrscheinlichkeiten dieser Werte. An Haltepunkten der Funktion F(X) bleibt kontinuierlich.

Der Graph der Verteilungsfunktion einer kontinuierlichen Zufallsvariablen ist eine kontinuierliche Kurve.

X

Reis. 3.2. Diagramm der Verteilungsfunktion einer kontinuierlichen Zufallsvariablen

Die Verteilungsfunktion hat die folgenden offensichtlichen Eigenschaften:

1) , 2) , 3) ,

4) bei .

Wir nennen das Ereignis eine Zufallsvariable X Nimmt den Wert an X, Zugehörigkeit zu einem halbgeschlossenen Intervall A£ X< B, Wenn eine Zufallsvariable in das Intervall [ A, B).

Satz 3.1. Die Wahrscheinlichkeit, dass eine Zufallsvariable in das Intervall [ A, B) ist gleich dem Inkrement der Verteilungsfunktion in diesem Intervall:

Wenn Sie das Intervall verkürzen [ A, B), Unter der Annahme, dass , dann ergibt sich in der Grenzformel (3.1) anstelle der Wahrscheinlichkeit, das Intervall zu treffen, die Wahrscheinlichkeit, den Punkt zu treffen, d. h. die Wahrscheinlichkeit, dass die Zufallsvariable den Wert annimmt A:

Wenn die Verteilungsfunktion an der Stelle eine Diskontinuität aufweist A, Dann ist Grenzwert (3.2) gleich dem Wert des Funktionssprungs F(X) am Punkt X=A, Das heißt, die Wahrscheinlichkeit, dass die Zufallsvariable den Wert annimmt A (Abb. 3.3, A). Wenn die Zufallsvariable stetig ist, ist die Funktion stetig F(X), dann ist der Grenzwert (3.2) gleich Null (Abb. 3.3, B)

Somit ist die Wahrscheinlichkeit eines bestimmten Wertes einer kontinuierlichen Zufallsvariablen Null. Dies bedeutet jedoch nicht, dass die Veranstaltung unmöglich ist X=A, Es heißt lediglich, dass die relative Häufigkeit dieses Ereignisses bei unbegrenzter Erhöhung der Anzahl der Tests gegen Null tendieren wird.

A)
B)

Reis. 3.3. Verteilungsfunktionssprung

Für kontinuierliche Zufallsvariablen wird neben der Verteilungsfunktion eine andere Form der Angabe des Verteilungsgesetzes verwendet – die Verteilungsdichte.

Ist die Wahrscheinlichkeit, in das Intervall zu fallen, dann charakterisiert das Verhältnis die Dichte, mit der die Wahrscheinlichkeit in der Umgebung des Punktes verteilt ist X. Die Grenze dieses Verhältnisses liegt bei, d.h. h. Ableitung, heißt Verteilungsdichte(Wahrscheinlichkeitsverteilungsdichte, Wahrscheinlichkeitsdichte) einer Zufallsvariablen X. Lassen Sie uns vereinbaren, die Verteilungsdichte zu bezeichnen

.

Somit charakterisiert die Verteilungsdichte die Wahrscheinlichkeit, dass eine Zufallsvariable in die Nähe eines Punktes fällt X.

Der Verteilungsdichtegraph heißt Krumme RennenGrenzen(Abb. 3.4).

Reis. 3.4. Art der Verteilungsdichte

Basierend auf der Definition und den Eigenschaften der Verteilungsfunktion F(X) lassen sich leicht die folgenden Eigenschaften der Verteilungsdichte ermitteln F(X):

1) F(X)³0

2)

3)

4)

Da für eine kontinuierliche Zufallsvariable die Wahrscheinlichkeit, einen Punkt zu treffen, Null ist, gelten die folgenden Gleichungen:

Beispiel 3.2. Zufälliger Wert X Gegeben durch die Verteilungsdichte

Erforderlich:

A) Finden Sie den Wert des Koeffizienten A;

B) Finden Sie die Verteilungsfunktion;

C) Finden Sie die Wahrscheinlichkeit, dass eine Zufallsvariable auf das Intervall (0, ) fällt.

Die Verteilungsfunktion oder Verteilungsdichte beschreibt eine Zufallsvariable vollständig. Bei praktischen Entscheidungen ist jedoch häufig keine vollständige Kenntnis des Verteilungsgesetzes erforderlich; es reicht aus, nur einige seiner charakteristischen Merkmale zu kennen. Zu diesem Zweck nutzt die Wahrscheinlichkeitstheorie numerische Merkmale einer Zufallsvariablen, die verschiedene Eigenschaften des Verteilungsgesetzes ausdrücken. Die wichtigsten numerischen Merkmale sind MathematischErwartung, Varianz und Standardabweichung.

Erwarteter Wert Charakterisiert die Position einer Zufallsvariablen auf der Zahlenachse. Dies ist ein Durchschnittswert einer Zufallsvariablen, um den alle möglichen Werte gruppiert sind.

Erwartung einer Zufallsvariablen X Durch Symbole gekennzeichnet M(X) oder T. Der mathematische Erwartungswert einer diskreten Zufallsvariablen ist die Summe gepaarter Produkte aller möglichen Werte der Zufallsvariablen und der Wahrscheinlichkeiten dieser Werte:

Der mathematische Erwartungswert einer kontinuierlichen Zufallsvariablen wird mithilfe eines unechten Integrals bestimmt:

Anhand der Definitionen lässt sich die Gültigkeit der folgenden Eigenschaften der mathematischen Erwartung leicht überprüfen:

1. (mathematische Erwartung eines nicht zufälligen Wertes MIT Entspricht dem am wenigsten zufälligen Wert).

2. Wenn ³0, dann ³0.

4. Wenn und Unabhängig, Das .

Beispiel 3.3. Finden Sie den mathematischen Erwartungswert einer diskreten Zufallsvariablen, die durch die Verteilungsreihe gegeben ist:

Lösung.

=0×0,2 + 1×0,4 + 2×0,3 + 3×0,1=1,3.

Beispiel 3.4. Finden Sie den mathematischen Erwartungswert einer Zufallsvariablen, die durch die Verteilungsdichte gegeben ist:

.

Lösung.

Varianz und Standardabweichung Sie sind Merkmale der Streuung einer Zufallsvariablen; sie charakterisieren die Streuung ihrer möglichen Werte relativ zur mathematischen Erwartung.

Varianz D(X) Zufällige Variable X Der mathematische Erwartungswert der quadratischen Abweichung einer Zufallsvariablen von ihrem mathematischen Erwartungswert heißt. Bei einer diskreten Zufallsvariablen wird die Varianz durch die Summe ausgedrückt:

(3.3)

Und für kontinuierlich – durch das Integral

(3.4)

Die Varianz hat die Dimension des Quadrats der Zufallsvariablen. Dispersionseigenschaften Gleiche GrößeSti mit einer Zufallsvariablen, dient als Standardabweichung.

Dispersionseigenschaften:

1) – konstant. Insbesondere,

3)

Insbesondere,

Beachten Sie, dass sich die Berechnung der Varianz mithilfe der Formel (3.5) häufig als bequemer erweist als die Verwendung der Formeln (3.3) oder (3.4).

Die Menge wird aufgerufen Kovarianz zufällige Variablen.

Wenn , dann der Wert

Angerufen Korrelationskoeffizient zufällige Variablen.

Es kann gezeigt werden, dass wenn , dann sind die Größen linear abhängig: wo

Beachten Sie, dass, wenn sie unabhängig sind, dann

Beispiel 3.5. Finden Sie die Varianz der Zufallsvariablen, die durch die Verteilungsreihe aus Beispiel 1 gegeben ist.

Lösung. Um die Varianz zu berechnen, müssen Sie den mathematischen Erwartungswert kennen. Für eine gegebene Zufallsvariable wurde oben gefunden: M=1,3. Wir berechnen die Varianz nach Formel (3.5):

Beispiel 3.6. Die Zufallsvariable wird durch die Verteilungsdichte angegeben

Finden Sie die Varianz und Standardabweichung.

Lösung. Zuerst finden wir den mathematischen Erwartungswert:

(als Integral einer ungeraden Funktion über ein symmetrisches Intervall).

Jetzt berechnen wir die Varianz und Standardabweichung:

1. Binomialverteilung. Die Zufallsvariable, die der Anzahl der „ERFOLGE“ im Bernoulli-Schema entspricht, hat eine Binomialverteilung: , .

Der mathematische Erwartungswert einer nach dem Binomialgesetz verteilten Zufallsvariablen ist gleich

.

Die Varianz dieser Verteilung beträgt .

2. Poisson-Verteilung ,

Erwartungswert und Varianz einer Zufallsvariablen mit Poisson-Verteilung, .

Die Poisson-Verteilung wird häufig verwendet, wenn es um die Anzahl von Ereignissen geht, die in einem bestimmten Zeitraum oder Raum auftreten, zum Beispiel: die Anzahl der Autos, die in einer Stunde in einer Autowaschanlage ankommen, die Anzahl der Maschinenstopps pro Woche, die Anzahl von Verkehrsunfällen usw.

Die Zufallsvariable hat Geometrische Verteilung mit Parameter, wenn es Werte mit Wahrscheinlichkeiten annimmt . Eine Zufallsvariable mit einer solchen Verteilung ist sinnvoll Zahlen des ersten erfolgreichen Tests im Bernoulli-Schema mit der Erfolgswahrscheinlichkeit. Die Verteilungstabelle sieht so aus:

3. Normalverteilung. Unter den anderen Verteilungsgesetzen nimmt das Normalgesetz der Wahrscheinlichkeitsverteilung eine Sonderstellung ein. In der Wahrscheinlichkeitstheorie ist bewiesen, dass die Wahrscheinlichkeitsdichte der Summe unabhängiger oder Leicht abhängig, gleichmäßig kleine (d. h. ungefähr die gleiche Rolle spielende) Terme kommen bei unbegrenzter Zunahme ihrer Anzahl dem Normalverteilungsgesetz so nahe wie gewünscht, unabhängig davon, welche Verteilungsgesetze diese Terme haben (zentraler Grenzwertsatz von A. M. Lyapunov).

Zufällige Variable ist eine Variable, die abhängig von verschiedenen Umständen bestimmte Werte annehmen kann, und Eine Zufallsvariable heißt kontinuierlich , wenn es einen beliebigen Wert aus einem begrenzten oder unbegrenzten Intervall annehmen kann. Für eine kontinuierliche Zufallsvariable ist es unmöglich, alle möglichen Werte anzugeben, daher bezeichnen wir Intervalle dieser Werte, die mit bestimmten Wahrscheinlichkeiten verbunden sind.

Beispiele für kontinuierliche Zufallsvariablen sind: der Durchmesser eines Teils, das auf eine bestimmte Größe geschliffen wird, die Größe einer Person, die Flugreichweite eines Projektils usw.

Da für kontinuierliche Zufallsvariablen die Funktion F(X), im Gegensatz zu diskrete Zufallsvariablen, nirgendwo Sprünge aufweist, ist die Wahrscheinlichkeit eines einzelnen Wertes einer kontinuierlichen Zufallsvariablen Null.

Das bedeutet, dass es für eine kontinuierliche Zufallsvariable keinen Sinn macht, über die Wahrscheinlichkeitsverteilung zwischen ihren Werten zu sprechen: Jeder von ihnen hat eine Wahrscheinlichkeit von Null. In gewissem Sinne gibt es jedoch unter den Werten einer kontinuierlichen Zufallsvariablen „mehr und weniger wahrscheinlich“. Kaum jemand würde beispielsweise daran zweifeln, dass der Wert einer Zufallsvariablen – die Körpergröße einer zufällig angetroffenen Person – 170 cm – wahrscheinlicher ist als 220 cm, obwohl beide Werte in der Praxis vorkommen können.

Verteilungsfunktion einer kontinuierlichen Zufallsvariablen und Wahrscheinlichkeitsdichte

Als Verteilungsgesetz, das nur für kontinuierliche Zufallsvariablen sinnvoll ist, wird der Begriff der Verteilungsdichte oder Wahrscheinlichkeitsdichte eingeführt. Gehen wir es an, indem wir die Bedeutung der Verteilungsfunktion für eine kontinuierliche Zufallsvariable und für eine diskrete Zufallsvariable vergleichen.

Also die Verteilungsfunktion einer Zufallsvariablen (sowohl diskret als auch kontinuierlich) oder Integralfunktion heißt eine Funktion, die die Wahrscheinlichkeit bestimmt, dass der Wert einer Zufallsvariablen ist X kleiner oder gleich dem Grenzwert ist X.

Für eine diskrete Zufallsvariable an den Punkten ihrer Werte X1 , X 2 , ..., X ich,... Massen von Wahrscheinlichkeiten sind konzentriert P1 , P 2 , ..., P ich,..., und die Summe aller Massen ist gleich 1. Übertragen wir diese Interpretation auf den Fall einer kontinuierlichen Zufallsvariablen. Stellen wir uns vor, dass eine Masse gleich 1 nicht an einzelnen Punkten konzentriert ist, sondern kontinuierlich entlang der Abszissenachse „verschmiert“ wird Oh mit etwas ungleichmäßiger Dichte. Wahrscheinlichkeit, dass eine Zufallsvariable in einen beliebigen Bereich Δ fällt X wird als Masse pro Abschnitt interpretiert und die durchschnittliche Dichte an diesem Abschnitt als Verhältnis von Masse zu Länge. Wir haben gerade ein wichtiges Konzept der Wahrscheinlichkeitstheorie eingeführt: die Verteilungsdichte.

Wahrscheinlichkeitsdichte F(X) einer kontinuierlichen Zufallsvariablen ist die Ableitung ihrer Verteilungsfunktion:

.

Wenn Sie die Dichtefunktion kennen, können Sie die Wahrscheinlichkeit ermitteln, dass der Wert einer kontinuierlichen Zufallsvariablen zum geschlossenen Intervall gehört [ A; B]:

die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable vorliegt X nimmt jeden Wert aus dem Intervall [ A; B], ist gleich einem bestimmten Integral seiner Wahrscheinlichkeitsdichte im Bereich von A Vor B:

.

In diesem Fall die allgemeine Formel der Funktion F(X) Wahrscheinlichkeitsverteilung einer kontinuierlichen Zufallsvariablen, die verwendet werden kann, wenn die Dichtefunktion bekannt ist F(X) :

.

Der Wahrscheinlichkeitsdichtegraph einer kontinuierlichen Zufallsvariablen wird als Verteilungskurve bezeichnet (Abbildung unten).

Fläche einer Figur (in der Abbildung schattiert), begrenzt durch eine Kurve, gerade Linien, die aus Punkten gezogen werden A Und B senkrecht zur x-Achse und zur Achse Oh, zeigt grafisch die Wahrscheinlichkeit an, dass der Wert einer kontinuierlichen Zufallsvariablen ist X liegt im Bereich von A Vor B.

Eigenschaften der Weiner kontinuierlichen Zufallsvariablen

1. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen beliebigen Wert aus dem Intervall (und der Fläche der Zahl, die durch den Graphen der Funktion begrenzt wird) annimmt F(X) und Achse Oh) ist gleich eins:

2. Die Wkann keine negativen Werte annehmen:

und außerhalb der Existenz der Verteilung ist ihr Wert Null

Verteilungsdichte F(X) sowie die Verteilungsfunktion F(X) ist eine der Formen des Verteilungsgesetzes, aber im Gegensatz zur Verteilungsfunktion ist es nicht universell: Die Verteilungsdichte existiert nur für kontinuierliche Zufallsvariablen.

Erwähnen wir die beiden in der Praxis wichtigsten Verteilungsarten einer kontinuierlichen Zufallsvariablen.

Wenn die Verteilungsdichtefunktion F(X) kontinuierliche Zufallsvariable in einem endlichen Intervall [ A; B] nimmt einen konstanten Wert an C, und außerhalb des Intervalls einen Wert gleich Null annimmt, dann dies die Verteilung heißt gleichmäßig .

Wenn der Graph der Verteilungsdichtefunktion symmetrisch zum Zentrum ist, konzentrieren sich die Durchschnittswerte in der Nähe des Zentrums, und wenn man sich vom Zentrum entfernt, werden diejenigen gesammelt, die stärker vom Durchschnitt abweichen (der Graph der Funktion ähnelt einem Abschnitt von a Glocke), dann das Die Verteilung heißt Normalverteilung .

Beispiel 1. Die Wahrsceiner kontinuierlichen Zufallsvariablen ist bekannt:

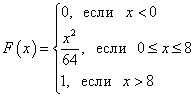
Funktion finden F(X) Wahrscheinlichkeitsdichte einer kontinuierlichen Zufallsvariablen. Konstruieren Sie Graphen beider Funktionen. Bestimmen Sie die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable einen beliebigen Wert im Intervall von 4 bis 8 annimmt: .

Lösung. Wir erhalten die Wahrscheinlichkeitsdichtefunktion, indem wir die Ableitung der Wahrscermitteln:

Graph einer Funktion F(X) - Parabel:

Graph einer Funktion F(X) - gerade:

Lassen Sie uns die Wahrscheinlichkeit ermitteln, dass eine kontinuierliche Zufallsvariable einen Wert im Bereich von 4 bis 8 annimmt:

Beispiel 2. Die Weiner kontinuierlichen Zufallsvariablen wird wie folgt angegeben:

Koeffizient berechnen C. Funktion finden F(X) Wahrscheinlichkeitsverteilung einer kontinuierlichen Zufallsvariablen. Konstruieren Sie Graphen beider Funktionen. Finden Sie die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable einen beliebigen Wert im Bereich von 0 bis 5 annimmt: .

Lösung. Koeffizient C Wir finden unter Verwendung der Eigenschaft 1 der Wahrscheinlichkeitsdichtefunktion:

Somit ist die Weiner kontinuierlichen Zufallsvariablen:

Durch Integration finden wir die Funktion F(X) Wahrscheinlichkeitsverteilungen. Wenn X < 0 , то F(X) = 0 . Wenn 0< X < 10 , то

.

X> 10 also F(X) = 1 .

Somit lautet der vollständige Datensatz der Wahrscheinlichkeitsverteilungsfunktion:

Graph einer Funktion F(X) :

Graph einer Funktion F(X) :

Lassen Sie uns die Wahrscheinlichkeit ermitteln, dass eine kontinuierliche Zufallsvariable einen Wert im Bereich von 0 bis 5 annimmt:

Beispiel 3. Wahrscheinlichkeitsdichte einer kontinuierlichen Zufallsvariablen X ist gegeben durch die Gleichheit , und . Finden Sie den Koeffizienten A, die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable X nimmt jeden Wert aus dem Intervall ]0, 5[, der Verteilungsfunktion einer kontinuierlichen Zufallsvariablen, an X.

Lösung. Durch die Bedingung gelangen wir zur Gleichheit

Daher , von wo . Also,

.

Jetzt ermitteln wir die Wahrscheinlichkeit, dass es sich um eine kontinuierliche Zufallsvariable handelt X nimmt jeden Wert aus dem Intervall ]0, 5[ an:

Jetzt erhalten wir die Verteilungsfunktion dieser Zufallsvariablen:

Beispiel 4. Ermitteln Sie die Wahrscheinlichkeitsdichte einer kontinuierlichen Zufallsvariablen X, das nur nichtnegative Werte annimmt, und seine Verteilungsfunktion .

In der Wahrscheinlichkeitstheorie hat man es mit Zufallsvariablen zu tun, deren Werte nicht alle aufgezählt werden können. Es ist beispielsweise unmöglich, alle Werte der Zufallsvariablen $X$ – der Betriebszeit der Uhr – zu nehmen und zu „iterieren“, da die Zeit in Stunden, Minuten, Sekunden, Millisekunden usw. gemessen werden kann. Sie können lediglich ein bestimmtes Intervall angeben, innerhalb dessen die Werte der Zufallsvariablen liegen.

Kontinuierliche Zufallsvariable ist eine Zufallsvariable, deren Werte ein bestimmtes Intervall vollständig ausfüllen.

Verteilungsfunktion einer kontinuierlichen Zufallsvariablen

Da es nicht möglich ist, alle Werte einer kontinuierlichen Zufallsvariablen aufzuzählen, kann diese mithilfe der Verteilungsfunktion angegeben werden.

Verteilungsfunktion Die Zufallsvariable $X$ wird als Funktion $F\left(x\right)$ bezeichnet, die die Wahrscheinlichkeit bestimmt, dass die Zufallsvariable $X$ einen Wert annimmt, der kleiner als ein fester Wert $x$ ist, also $F\ left(x\right )=P\left(X< x\right)$.

Eigenschaften der Verteilungsfunktion:

1 . $0\le F\left(x\right)\le 1$.

2 . Die Wahrscheinlichkeit, dass die Zufallsvariable $X$ Werte aus dem Intervall $\left(\alpha ;\ \beta \right)$ annimmt, ist gleich der Differenz zwischen den Werten der Verteilungsfunktion an den Enden dieses Intervalls Intervall: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$.

3 . $F\left(x\right)$ – nicht abnehmend.

4 . $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$.

Beispiel 1
0,\ x\le 0\\
x,\ 0< x\le 1\\
1,\ x>1
\end(matrix)\right.$. Die Wahrscheinlichkeit, dass eine Zufallsvariable $X$ in das Intervall $\left(0,3;0,7\right)$ fällt, kann als Differenz zwischen den Werten der Verteilungsfunktion $F\left(x\right)$ at ermittelt werden die Enden dieses Intervalls, das heißt:

$$P\left(0.3< X < 0,7\right)=F\left(0,7\right)-F\left(0,3\right)=0,7-0,3=0,4.$$

Wahrscheinlichkeitsverteilungsdichte

Die Funktion $f\left(x\right)=(F)"(x)$ wird Wahrgenannt, das heißt, sie ist die Ableitung erster Ordnung aus der Verteilungsfunktion $F\left(x\right )$ selbst.

Eigenschaften der Funktion $f\left(x\right)$.

1 . $f\left(x\right)\ge 0$.

2 . $\int^x_(-\infty )(f\left(t\right)dt)=F\left(x\right)$.

3 . Die Wahrscheinlichkeit, dass die Zufallsvariable $X$ Werte aus dem Intervall $\left(\alpha ;\ \beta \right)$ annimmt, beträgt $P\left(\alpha< X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Геометрически это означает, что вероятность попадания случайной величины $X$ в интервал $\left(\alpha ;\ \beta \right)$ равна площади криволинейной трапеции, которая будет ограничена графиком функции $f\left(x\right)$, прямыми $x=\alpha ,\ x=\beta $ и осью $Ox$.

4 . $\int^(+\infty )_(-\infty )(f\left(x\right))=1$.

Beispiel 2 . Eine kontinuierliche Zufallsvariable $X$ wird durch die folgende Verteilungsfunktion $F(x)=\left\(\begin(matrix) definiert
0,\ x\le 0\\
x,\ 0< x\le 1\\
1,\ x>1
\end(matrix)\right.$. Dann ist die Dichtefunktion $f\left(x\right)=(F)"(x)=\left\(\begin(matrix)
0,\x\le 0\\
1,\ 0 < x\le 1\\
0.\x>1
\end(matrix)\right.$

Erwartung einer kontinuierlichen Zufallsvariablen

Der mathematische Erwartungswert einer kontinuierlichen Zufallsvariablen $X$ wird mithilfe der Formel berechnet

$$M\left(X\right)=\int^(+\infty )_(-\infty )(xf\left(x\right)dx).$$

Beispiel 3 . Finden wir $M\left(X\right)$ für die Zufallsvariable $X$ aus Beispiel $2$.

$$M\left(X\right)=\int^(+\infty )_(-\infty )(xf\left(x\right)\ dx)=\int^1_0(x\ dx)=(( x^2)\over (2))\bigg|_0^1=((1)\over (2)).$$

Varianz einer kontinuierlichen Zufallsvariablen

Die Varianz einer kontinuierlichen Zufallsvariablen $X$ wird durch die Formel berechnet

$$D\left(X\right)=\int^(+\infty )_(-\infty )(x^2f\left(x\right)\ dx)-(\left)^2.$$

Beispiel 4 . Finden wir $D\left(X\right)$ für die Zufallsvariable $X$ aus Beispiel $2$.

$$D\left(X\right)=\int^(+\infty )_(-\infty )(x^2f\left(x\right)\ dx)-(\left)^2=\int^ 1_0(x^2\ dx)-(\left(((1)\over (2))\right))^2=((x^3)\over (3))\bigg|_0^1-( (1)\over (4))=((1)\over (3))-((1)\over (4))=((1)\over(12)).$$

ZUFÄLLIGE VARIABLEN

Beispiel 2.1. Zufälliger Wert X gegeben durch die Verteilungsfunktion

Finden Sie die Wahrscheinlichkeit, dass das Ergebnis des Tests vorliegt X nimmt Werte an, die im Intervall (2,5; 3,6) enthalten sind.

Lösung: X im Intervall (2,5; 3,6) kann auf zwei Arten bestimmt werden:

Beispiel 2.2. Bei welchen Parameterwerten A Und IN Funktion F(X) = A + Be - x kann eine Verteilungsfunktion für nicht negative Werte einer Zufallsvariablen sein X.

Lösung: Da alle möglichen Werte der Zufallsvariablen X zum Intervall gehören, damit die Funktion eine Verteilungsfunktion für ist X, die Eigenschaft muss erfüllt sein:

.

Antwort: .

Beispiel 2.3. Die Zufallsvariable X wird durch die Verteilungsfunktion angegeben

Ermitteln Sie die Wahrscheinlichkeit, dass als Ergebnis von vier unabhängigen Tests der Wert erreicht wird X genau 3 Mal wird ein Wert angenommen, der zum Intervall (0,25;0,75) gehört.

Lösung: Wahrscheinlichkeit, einen Wert zu erreichen X im Intervall (0,25;0,75) finden wir mit der Formel:

Beispiel 2.4. Die Wahrscheinlichkeit, dass der Ball mit einem Schlag den Korb trifft, beträgt 0,3. Stellen Sie ein Verteilungsgesetz für die Anzahl der Treffer bei drei Würfen auf.

Lösung: Zufälliger Wert X– die Anzahl der Treffer im Korb bei drei Schüssen – kann folgende Werte annehmen: 0, 1, 2, 3. Wahrscheinlichkeiten, die X

X:

Beispiel 2.5. Zwei Schützen geben jeweils einen Schuss auf ein Ziel ab. Die Wahrscheinlichkeit, dass der erste Schütze es trifft, beträgt 0,5, die zweite - 0,4. Erstellen Sie ein Verteilungsgesetz für die Anzahl der Treffer auf einer Zielscheibe.

Lösung: Finden wir das Verteilungsgesetz einer diskreten Zufallsvariablen X– Anzahl der Treffer auf das Ziel. Lassen Sie das Ereignis darin bestehen, dass der erste Schütze das Ziel trifft, und lassen Sie den zweiten Schützen das Ziel treffen bzw. verfehlen.



Lassen Sie uns das Gesetz der Wahrscheinlichkeitsverteilung von SV aufstellen X:

Beispiel 2.6. Es werden drei Elemente getestet, die unabhängig voneinander arbeiten. Die Zeitdauer (in Stunden) des störungsfreien Betriebs von Elementen hat eine Verteilungsdichtefunktion: Zum ersten: F 1 (T) =1-e- 0,1 T, zum zweiten: F 2 (T) = 1-e- 0,2 T, für den dritten: F 3 (T) =1-e- 0,3 T. Finden Sie die Wahrscheinlichkeit, dass im Zeitintervall von 0 bis 5 Stunden: nur ein Element ausfällt; nur zwei Elemente werden scheitern; Alle drei Elemente werden scheitern.

Lösung: Verwenden wir die Definition der Wahrscheinlichkeitserzeugungsfunktion:

Die Wahrscheinlichkeit, dass in unabhängigen Versuchen, im ersten davon die Wahrscheinlichkeit, dass ein Ereignis eintritt A gleich, im zweiten usw. Ereignis A erscheint genau einmal, gleich dem Koeffizienten in der Entwicklung der erzeugenden Funktion in Potenzen von . Ermitteln wir die Ausfallwahrscheinlichkeiten bzw. Nichtausfallwahrscheinlichkeiten des ersten, zweiten und dritten Elements im Zeitintervall von 0 bis 5 Stunden:

Lassen Sie uns eine erzeugende Funktion erstellen:

Der Koeffizient at entspricht der Wahrscheinlichkeit, dass das Ereignis eintritt A erscheint genau dreimal, d. h. die Ausfallwahrscheinlichkeit aller drei Elemente; der Koeffizient at ist gleich der Wahrscheinlichkeit, dass genau zwei Elemente ausfallen; Der Koeffizient at entspricht der Wahrscheinlichkeit, dass nur ein Element ausfällt.

Beispiel 2.7. Angesichts der Wahrscheinlichkeitsdichte F(X)zufällige Variable X:

Finden Sie die Verteilungsfunktion F(x).

Lösung: Wir verwenden die Formel:

.

Somit sieht die Verteilungsfunktion wie folgt aus:

Beispiel 2.8. Das Gerät besteht aus drei unabhängig voneinander arbeitenden Elementen. Die Ausfallwahrscheinlichkeit jedes Elements in einem Experiment beträgt 0,1. Erstellen Sie ein Verteilungsgesetz für die Anzahl der fehlgeschlagenen Elemente in einem Experiment.

Lösung: Zufälliger Wert X– die Anzahl der Elemente, die in einem Experiment versagt haben – kann die folgenden Werte annehmen: 0, 1, 2, 3. Wahrscheinlichkeiten, die X nimmt diese Werte an, finden wir mithilfe der Bernoulli-Formel:

Somit erhalten wir das folgende Gesetz der Wahrscheinlichkeitsverteilung einer Zufallsvariablen X:

Beispiel 2.9. In einer Charge von 6 Teilen gibt es 4 Standardteile. 3 Teile wurden zufällig ausgewählt. Erstellen Sie ein Verteilungsgesetz für die Anzahl der Normteile unter den ausgewählten.

Lösung: Zufälliger Wert X– die Anzahl der Normteile unter den ausgewählten – kann die folgenden Werte annehmen: 1, 2, 3 und hat eine hypergeometrische Verteilung. Wahrscheinlichkeiten, die X

Wo -- Anzahl der Teile in der Charge;

-- Anzahl der Normteile in einer Charge;

– Anzahl der ausgewählten Teile;

-- Anzahl der Normteile unter den ausgewählten.

.

.

.

Beispiel 2.10. Die Zufallsvariable hat eine Verteilungsdichte

und sind nicht bekannt, aber , a und . Finden und.

Lösung: In diesem Fall die Zufallsvariable X hat eine Dreiecksverteilung (Simpson-Verteilung) auf dem Intervall [ a, b]. Numerische Eigenschaften X:

Somit, . Wenn wir dieses System lösen, erhalten wir zwei Wertepaare: . Denn entsprechend den Bedingungen des Problems haben wir schließlich: .

Antwort: .

Beispiel 2.11. Im Durchschnitt zahlt die Versicherungsgesellschaft bei weniger als 10 % der Verträge Versicherungsbeträge im Zusammenhang mit dem Eintritt eines Versicherungsfalls. Berechnen Sie die mathematische Erwartung und Streuung der Anzahl solcher Verträge unter vier zufällig ausgewählten Verträgen.

Lösung: Der mathematische Erwartungswert und die Varianz können mithilfe der Formeln ermittelt werden:

.

Mögliche Werte von SV (Anzahl der Verträge (von vier) mit Eintritt eines Versicherungsfalls): 0, 1, 2, 3, 4.

Wir verwenden die Formel von Bernoulli, um die Wahrscheinlichkeiten für unterschiedlich viele Verträge (von vier) zu berechnen, für die die Versicherungsbeträge gezahlt wurden:

.

Die IC-Verteilungsreihe (Anzahl der Verträge mit Eintritt eines Versicherungsfalls) hat die Form:

0,6561 0,2916 0,0486 0,0036 0,0001

Antwort: , .

Beispiel 2.12. Von den fünf Rosen sind zwei weiß. Erstellen Sie ein Verteilungsgesetz für eine Zufallsvariable, das die Anzahl der weißen Rosen unter zwei gleichzeitig genommenen Rosen ausdrückt.

Lösung: Bei einer Auswahl von zwei Rosen kann es sein, dass entweder keine weiße Rose oder eine oder zwei weiße Rosen vorhanden sind. Daher die Zufallsvariable X kann Werte annehmen: 0, 1, 2. Wahrscheinlichkeiten, die X nimmt diese Werte an, wir finden sie mit der Formel:

Wo -- Anzahl Rosen;

-- Anzahl weißer Rosen;

– Anzahl der gleichzeitig entnommenen Rosen;

-- die Anzahl der weißen Rosen unter den Genommenen.

.

.

.

Dann lautet das Verteilungsgesetz der Zufallsvariablen wie folgt:

Beispiel 2.13. Von den 15 zusammengebauten Einheiten benötigen 6 eine zusätzliche Schmierung. Erstellen Sie ein Verteilungsgesetz für die Anzahl der Einheiten, die eine zusätzliche Schmierung benötigen, unter fünf zufällig ausgewählten Einheiten aus der Gesamtzahl.

Lösung: Zufälliger Wert X– die Anzahl der Einheiten, die unter den fünf ausgewählten Einheiten zusätzliche Schmierung benötigen – kann die folgenden Werte annehmen: 0, 1, 2, 3, 4, 5 und weist eine hypergeometrische Verteilung auf. Wahrscheinlichkeiten, die X nimmt diese Werte an, wir finden sie mit der Formel:

Wo -- Anzahl der zusammengebauten Einheiten;

-- die Anzahl der Einheiten, die zusätzliche Schmierung benötigen;

– Anzahl der ausgewählten Einheiten;

-- die Anzahl der ausgewählten Einheiten, die eine zusätzliche Schmierung benötigen.

.

.

.

.

.

.

Dann lautet das Verteilungsgesetz der Zufallsvariablen wie folgt:

Beispiel 2.14. Von den 10 zur Reparatur eingegangenen Uhren erfordern 7 eine allgemeine Reinigung des Mechanismus. Die Uhren sind nicht nach Reparaturart sortiert. Der Meister, der Uhren finden möchte, die gereinigt werden müssen, untersucht sie einzeln und stoppt die weitere Betrachtung, nachdem er solche Uhren gefunden hat. Ermitteln Sie den mathematischen Erwartungswert und die Varianz der Anzahl der angesehenen Stunden.

Lösung: Zufälliger Wert X– die Anzahl der Einheiten, die unter den fünf ausgewählten Einheiten zusätzliche Schmierung benötigen – kann die folgenden Werte annehmen: 1, 2, 3, 4. Wahrscheinlichkeiten, dass X nimmt diese Werte an, wir finden sie mit der Formel:

.

.

.

.

Dann lautet das Verteilungsgesetz der Zufallsvariablen wie folgt:

Berechnen wir nun die numerischen Eigenschaften der Menge:

Antwort: , .

Beispiel 2.15. Der Teilnehmer hat die letzte Ziffer der benötigten Telefonnummer vergessen, erinnert sich aber, dass sie seltsam ist. Ermitteln Sie den mathematischen Erwartungswert und die Varianz der Häufigkeit, mit der er eine Telefonnummer wählt, bevor er die gewünschte Nummer erreicht, wenn er die letzte Ziffer zufällig wählt und anschließend die gewählte Ziffer nicht wählt.

Lösung: Die Zufallsvariable kann folgende Werte annehmen: . Da der Teilnehmer die gewählte Ziffer in Zukunft nicht mehr wählt, sind die Wahrscheinlichkeiten dieser Werte gleich.

Lassen Sie uns eine Verteilungsreihe einer Zufallsvariablen erstellen:

0,2

Berechnen wir den mathematischen Erwartungswert und die Varianz der Anzahl der Wählversuche:

Antwort: , .

Beispiel 2.16. Die Wahrscheinlichkeit eines Ausfalls während der Zuverlässigkeitsprüfung ist für jedes Gerät in der Serie gleich P. Bestimmen Sie die mathematische Erwartung der Anzahl der Geräte, die ausgefallen sind, wenn sie getestet wurden N Geräte.

Lösung: Die diskrete Zufallsvariable X ist die Anzahl der ausgefallenen Geräte in N unabhängige Tests, bei denen die Ausfallwahrscheinlichkeit jeweils gleich ist P, nach dem Binomialgesetz verteilt. Der mathematische Erwartungswert einer Binomialverteilung ist gleich der Anzahl der Versuche multipliziert mit der Wahrscheinlichkeit, dass ein Ereignis in einem Versuch auftritt:

Beispiel 2.17. Diskrete Zufallsvariable X nimmt 3 mögliche Werte an: mit Wahrscheinlichkeit; mit Wahrscheinlichkeit und mit Wahrscheinlichkeit. Finden Sie und , wissend, dass M( X) = 8.

Lösung: Wir verwenden die Definitionen des mathematischen Erwartungswerts und des Verteilungsgesetzes einer diskreten Zufallsvariablen:

Wir finden: .

Beispiel 2.18. Die technische Kontrollabteilung prüft die Produkte auf Standardmäßigkeit. Die Wahrscheinlichkeit, dass das Produkt Standard ist, beträgt 0,9. Jede Charge enthält 5 Produkte. Finden Sie den mathematischen Erwartungswert einer Zufallsvariablen X– die Anzahl der Chargen, die jeweils genau 4 Standardprodukte enthalten, wenn 50 Chargen kontrollpflichtig sind.

Lösung: In diesem Fall sind alle durchgeführten Experimente unabhängig und die Wahrscheinlichkeiten, dass jede Charge genau 4 Standardprodukte enthält, sind gleich, daher kann die mathematische Erwartung durch die Formel bestimmt werden:

,

wo ist die Anzahl der Parteien;

Die Wahrscheinlichkeit, dass eine Charge genau 4 Standardprodukte enthält.

Wir ermitteln die Wahrscheinlichkeit mithilfe der Bernoulli-Formel:

Antwort: .

Beispiel 2.19. Finden Sie die Varianz einer Zufallsvariablen X– Anzahl der Vorkommnisse des Ereignisses A in zwei unabhängigen Versuchen, wenn die Wahrscheinlichkeiten für das Eintreten eines Ereignisses in diesen Versuchen gleich sind und dies bekannt ist M(X) = 0,9.

Lösung: Das Problem kann auf zwei Arten gelöst werden.

1) Mögliche Werte von SV X: 0, 1, 2. Mit der Bernoulli-Formel bestimmen wir die Wahrscheinlichkeiten dieser Ereignisse:

, , .

Dann das Verteilungsgesetz X hat die Form:

Aus der Definition der mathematischen Erwartung ermitteln wir die Wahrscheinlichkeit:

Lassen Sie uns die Streuung von SV ermitteln X:

.

2) Sie können die Formel verwenden:

.

Antwort: .

Beispiel 2.20. Erwartungswert und Standardabweichung einer normalverteilten Zufallsvariablen X jeweils gleich 20 und 5. Finden Sie die Wahrscheinlichkeit, dass als Ergebnis des Tests X nimmt den im Intervall (15; 25) enthaltenen Wert an.

Lösung: Wahrscheinlichkeit, eine normale Zufallsvariable zu treffen X auf dem Abschnitt von bis wird durch die Laplace-Funktion ausgedrückt:

Beispiel 2.21. Gegebene Funktion:

Bei welchem ​​Parameterwert C Diese Funktion ist die Verteilungsdichte einer kontinuierlichen Zufallsvariablen X? Finden Sie den mathematischen Erwartungswert und die Varianz einer Zufallsvariablen X.

Lösung: Damit eine Funktion die Verteilungsdichte einer Zufallsvariablen darstellt, darf sie nicht negativ sein und die folgende Eigenschaft erfüllen:

.

Somit:

Berechnen wir den mathematischen Erwartungswert anhand der Formel:

.

Berechnen wir die Varianz mit der Formel:

T ist gleich P. Es ist notwendig, den mathematischen Erwartungswert und die Varianz dieser Zufallsvariablen zu ermitteln.

Lösung: Das Verteilungsgesetz einer diskreten Zufallsvariablen Der mathematische Erwartungswert der Binomialverteilung ist gleich dem Produkt aus der Anzahl der Versuche und der Wahrscheinlichkeit des Auftretens von Ereignis A in einem Versuch:

.

Beispiel 2.25. Es werden drei unabhängige Schüsse auf das Ziel abgefeuert. Die Wahrscheinlichkeit, jeden Schuss zu treffen, beträgt 0,25. Bestimmen Sie die Standardabweichung der Trefferzahl bei drei Schüssen.

Lösung: Da drei unabhängige Versuche durchgeführt werden und die Wahrscheinlichkeit des Auftretens von Ereignis A (einem Treffer) in jedem Versuch gleich ist, gehen wir davon aus, dass die diskrete Zufallsvariable X – die Anzahl der Treffer auf dem Ziel – entsprechend verteilt ist Binomialgesetz.

Die Varianz der Binomialverteilung ist gleich dem Produkt aus der Anzahl der Versuche und der Wahrscheinlichkeit des Eintretens und Nichteintretens eines Ereignisses in einem Versuch:

Beispiel 2.26. Die durchschnittliche Anzahl der Kunden, die innerhalb von 10 Minuten eine Versicherungsgesellschaft besuchen, beträgt drei. Ermitteln Sie die Wahrscheinlichkeit, dass in den nächsten 5 Minuten mindestens ein Kunde ankommt.

Durchschnittliche Anzahl an Kunden, die innerhalb von 5 Minuten eintreffen: . .

Beispiel 2.29. Die Wartezeit für eine Anwendung in der Prozessorwarteschlange folgt einem Exponentialverteilungsgesetz mit einem Durchschnittswert von 20 Sekunden. Ermitteln Sie die Wahrscheinlichkeit, dass die nächste (zufällige) Anfrage länger als 35 Sekunden auf dem Prozessor wartet.

Lösung: In diesem Beispiel die mathematische Erwartung und die Ausfallrate ist gleich.

Dann ist die gewünschte Wahrscheinlichkeit:

Beispiel 2.30. Eine Gruppe von 15 Studierenden tagt in einem Saal mit 20 Reihen à 10 Sitzplätzen. Jeder Schüler nimmt zufällig einen Platz in der Halle ein. Wie groß ist die Wahrscheinlichkeit, dass nicht mehr als drei Personen auf dem siebten Platz der Reihe stehen?

Lösung:

Beispiel 2.31.

Dann gilt nach der klassischen Wahrscheinlichkeitsdefinition:

Wo -- Anzahl der Teile in der Charge;

-- Anzahl der nicht standardmäßigen Teile in der Charge;

– Anzahl der ausgewählten Teile;

-- Anzahl der nicht standardmäßigen Teile unter den ausgewählten.

Dann lautet das Verteilungsgesetz der Zufallsvariablen wie folgt.



 

Es könnte nützlich sein zu lesen: