ტრაპეციის წვეროები. მასალა გეომეტრიაზე თემაზე "ტრაპეცია და მისი თვისებები". ტოლფერდა ტრაპეციის თვისებები
გ.ი. კოვალევა
ტრაპეციის თვისებების შესწავლის მეთოდი
სხვადასხვა ტესტებისა და გამოცდების მასალებში ძალიან ხშირად გვხვდება ტრაპეციული ამოცანები, რომელთა გადაწყვეტა მოსწავლეებს მოითხოვს ტრაპეციის „არაპროგრამული“ თვისებების ცოდნას. (თვისებები ითვლება შუა ხაზიტრაპეცია, ტოლფერდა ტრაპეციის დიაგონალების და კუთხეების თვისებები.) რა ღირსშესანიშნავი თვისებები აქვს ტრაპეციას? სად და როდის შევისწავლოთ ისინი სკოლის გეომეტრიის კურსზე?
ტრაპეციის თვისებების შესწავლის მეთოდი
ახლა, როდესაც ვნახეთ რამდენიმე ტიპი, მოდით გავეცნოთ ფორმებს, რომლებსაც არ აქვთ პარალელოგრამების თვისებები. შეგახსენებთ, რომ პარალელოგრამები არის ოთხკუთხედები, რომელთა მოპირდაპირე გვერდები პარალელურია. ამ განყოფილებაში განვიხილავთ ოთხკუთხედებს, რომელთა მოპირდაპირე მხარეები შეიძლება იკვეთონ რაღაც მომენტში. დავიწყოთ ჩვენი შესწავლა ტრაპეციის ზოგიერთი თვისების შესწავლით. განმარტება. ტრაპეცია არის ოთხკუთხედი, რომელსაც აქვს ზუსტად ერთი წყვილი პარალელური გვერდი.
ტრაპეციის შუა ხაზის თვისებების შესწავლის შემდეგ შეგვიძლია ჩამოვაყალიბოთ და დავამტკიცოთ ტრაპეციის დიაგონალების შუა წერტილების დამაკავშირებელი სეგმენტის თვისება. ტრაპეციის დიაგონალების შუა წერტილების დამაკავშირებელი სეგმენტი უდრის ფუძეების ნახევრად სხვაობას.
ტრაპეციაზე „დახატეთ ორი სიმაღლე“ ამოცანების გადაჭრის ძირითადი ტექნიკის პრაქტიკაში, მოსწავლეებმა უნდა შესთავაზონ დავალება: „მოდით. BT- სიმაღლე ტოლფერდა ტრაპეცია Ა Ბ Გ Დსაფუძვლებით ძვ.წდა ახ.წ.
 ,
,
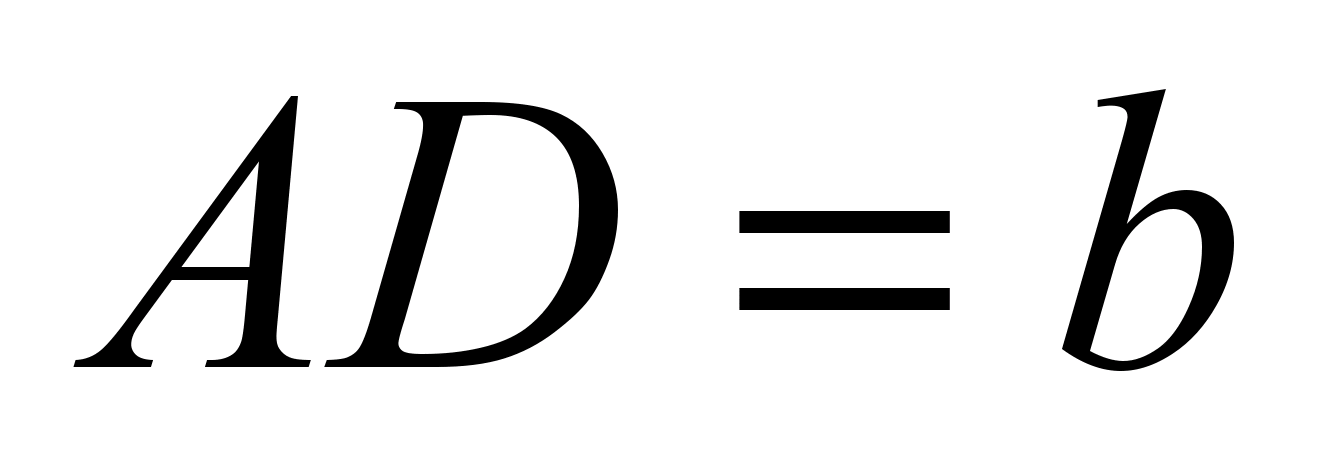 . იპოვეთ მონაკვეთების სიგრძე ATდა TD».
. იპოვეთ მონაკვეთების სიგრძე ATდა TD».
"ტრიგონომეტრიის გამოყენება პლანიმეტრიული ამოცანების გადაჭრაში"
ვინაიდან ტრაპეციას უნდა ჰქონდეს ზუსტად ერთი წყვილი პარალელური გვერდი, ჩვენ უნდა დავამტკიცოთ, რომ მოპირდაპირე გვერდების ერთი წყვილი პარალელურია და მეორე არ არის ჩვენში. თუ დაგვავიწყდება იმის მტკიცება, რომ ერთი წყვილი მოპირდაპირე გვერდი არ არის პარალელური, არ გამოვრიცხავთ შესაძლებლობას, რომ ოთხკუთხედი იყოს პარალელოგრამი. ამიტომ, ეს ნაბიჯი იქნება აბსოლუტურად აუცილებელი, რადგან ჩვენ ვმუშაობთ სხვადასხვა სავარჯიშოებზე, რომლებიც მოიცავს ტრაპეციას.
სანამ უშუალოდ ჩავუღრმავდებით ტრაპეციის შესწავლას, საჭირო იქნება ვიცოდეთ ამ ოთხკუთხედების სხვადასხვა ნაწილების სახელები, რათა კონკრეტულად ვიყოთ მისი გვერდებისა და კუთხეების შესახებ. ყველა ტრაპეცია შეიცავს ორ ძირითად ნაწილს: ფუძეს და ფეხებს. ტრაპეციის მოპირდაპირე მხარეებს, რომლებიც ერთმანეთის პარალელურია, ფუძეები ეწოდება. ტრაპეციის სხვა გვერდებს, რომლებიც იკვეთება რაღაც მომენტში, თუ ისინი დაგრძელებულნი არიან, ტრაპეციის ფეხები ეწოდება.
ტრაპეციის თვისებების შესასწავლად ძალიან სასარგებლოა თემა „ფიგურების მსგავსება“. მაგალითად, ტრაპეციის დიაგონალები ყოფს მას ოთხ სამკუთხედად და ფუძეების მიმდებარე სამკუთხედები მსგავსია, ხოლო გვერდების მიმდებარე სამკუთხედები ტოლია. დავარქვათ ეს განცხადება თანსამკუთხედების თვისება, რომლებშიც ტრაპეცია იყოფა დიაგონალებით. უფრო მეტიც, მტკიცების პირველი ნაწილი ძალიან მარტივად დასტურდება ორ კუთხით სამკუთხედების მსგავსების ნიშნით. მეორე ნაწილი მოსწავლეებს შეიძლება შევთავაზოთ დავალების სახით.
ჩამოყალიბებული ტრაპეციის სამკუთხედების მსგავსება
ტრაპეციის ზედა და ქვედა მხარეები ერთმანეთის პარალელურად გადის, ამიტომ ისინი ტრაპეციის ფუძეა. ტრაპეციის სხვა მხარეები იკვეთება, თუ ისინი დაგრძელებულნი არიან, ამიტომ ისინი ტრაპეციის ფეხებია. სეგმენტს, რომელიც აკავშირებს ტრაპეციის ფეხების შუა წერტილებს, ეწოდება შუა სეგმენტი. ამ სეგმენტის სიგრძე ყოველთვის უდრის ტრაპეციული ფუძეების ჯამის ნახევარს ან.
სეგმენტებისა და ფუძეების სიგრძის თანაფარდობა
შუა სეგმენტის გაზომვა დამოკიდებულია მხოლოდ ტრაპეციული ბაზების სიგრძეზე. თუმცა, არსებობს მნიშვნელოვანი მახასიათებელირომ ზოგიერთი ტრაპეცია მხოლოდ მის ფეხებზეა დამოკიდებული. მოდით შევხედოთ ამ ტრაპეციებს ახლა. ტოლფერდა ტრაპეცია არის ტრაპეცია, რომლის ფეხები კონგრუენტულია. განმარტებით, თუ ოთხკუთხედს აქვს ზუსტად ერთი წყვილი პარალელური წრფე, მაშინ ოთხკუთხედი არის ტრაპეცია. ტოლფერდა ტრაპეციის განმარტება ამატებს კიდევ ერთ სპეციფიკას: ტრაპეციის ფეხები უნდა იყოს კონგრუენტული.
ანალოგიურად, სამკუთხედები
BOCდა AOBაქვთ საერთო სიმაღლე, თუ მათ საფუძვლად ავიღებთ სეგმენტებს COდა OA.
მერე 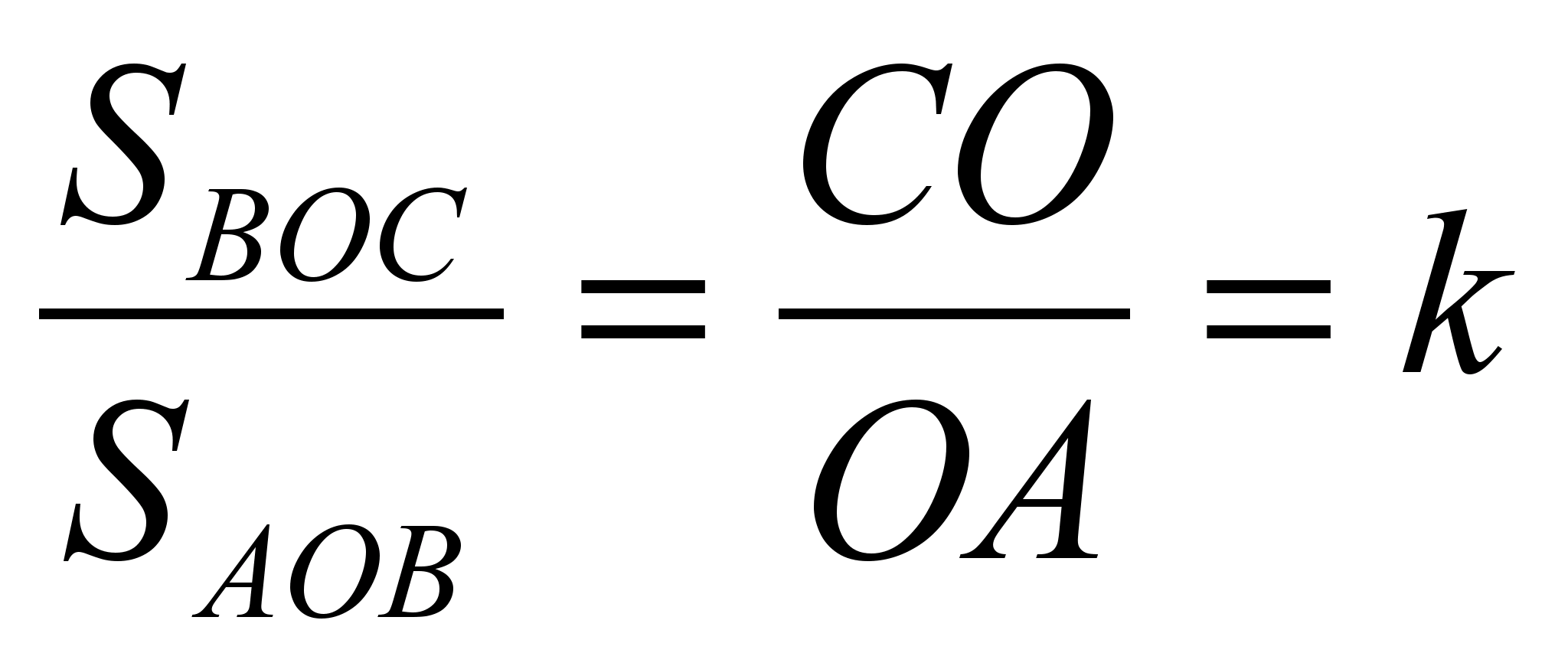 და
და 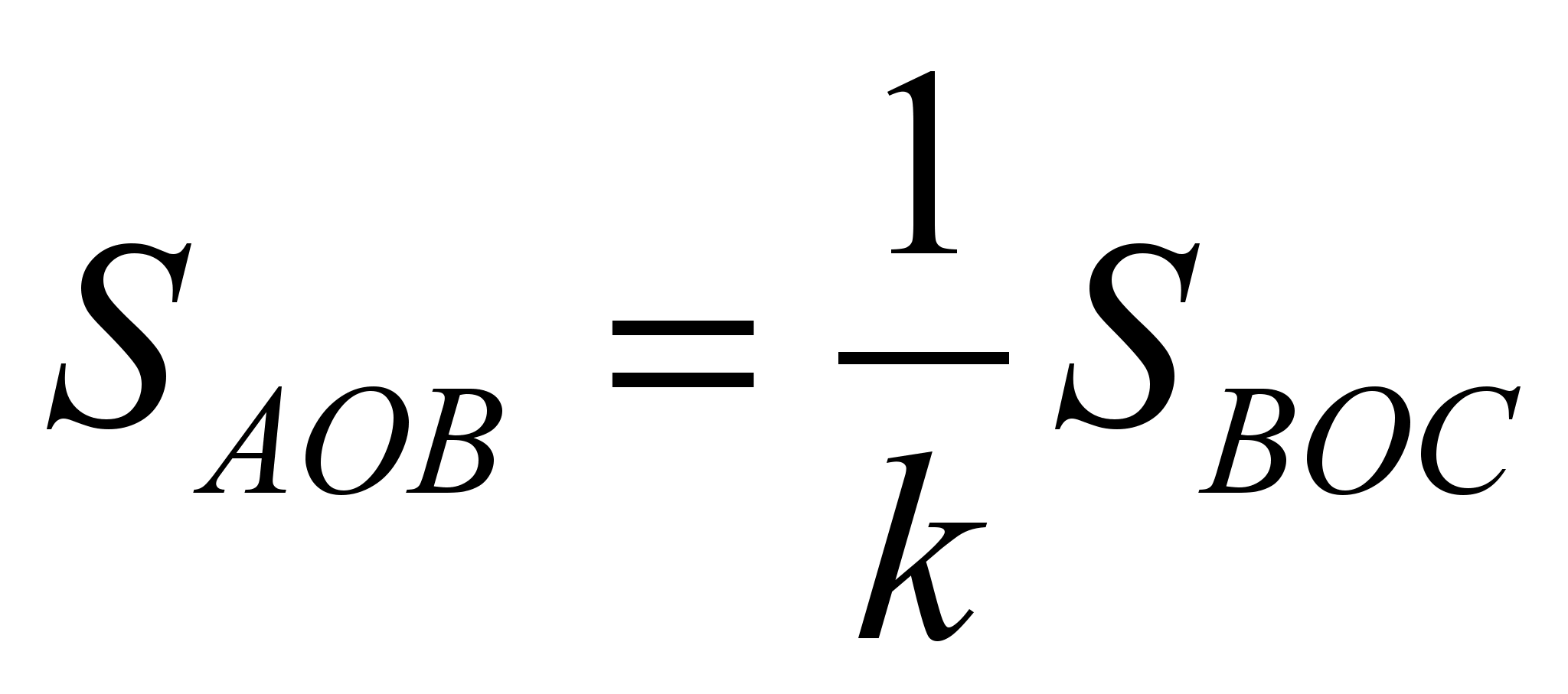 .
.
ამ ორი წინადადებიდან გამომდინარეობს, რომ 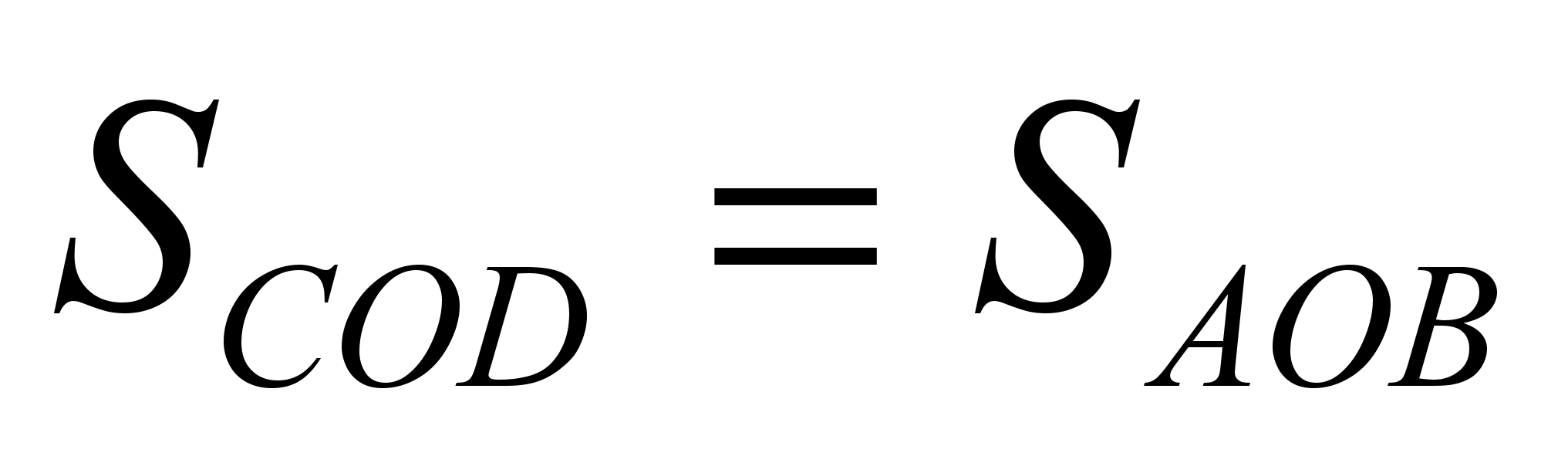 .
.
არსებობს რამდენიმე თეორემა, რომელიც შეგვიძლია გამოვიყენოთ, რათა დაგვეხმაროს დავამტკიცოთ, რომ ტრაპეცია ტოლფერდაა. ეს თვისებები ჩამოთვლილია ქვემოთ. ტრაპეცია ტოლფერდაა, თუ და მხოლოდ იმ შემთხვევაში, თუ ფუძის კუთხეები კონგრუენტულია. ტრაპეცია ტოლფერდაა, თუ და მხოლოდ მაშინ, თუ დიაგონალები კონგრუენტულია.
თუ ტრაპეცია ტოლფერდაა, მაშინ მისი მოპირდაპირე კუთხეები ერთმანეთს ავსებენ. Kite არის ოთხკუთხედი ორი განსხვავებული წყვილი მიმდებარე გვერდით, რომლებიც თანმიმდევრულია. შეგახსენებთ, რომ პარალელოგრამებს ასევე ჰქონდათ თანაბარი გვერდის წყვილი. თუმცა, მათი კონგრუტული მხარეები ყოველთვის საპირისპირო იყო. Kites-ს აქვს ორი წყვილი თანმიმდევრული მხარე, რომლებიც ხვდებიან ორ სხვადასხვა წერტილში. მოდით შევხედოთ ქვემოთ მოცემულ ილუსტრაციას, რათა დაგვეხმაროს გავიგოთ, როგორ გამოიყურება ფუტკარი.
კარგი იქნება, რომ არ შევჩერდეთ ჩამოყალიბებულ განცხადებაზე, არამედ ვიპოვოთ მიმართება სამკუთხედების უბნებს შორის, რომლებშიც ტრაპეცია იყოფა მისი დიაგონალებით
, იწვევს მოსწავლეებს ამოცანის გადასაჭრელად: „მოდით O იყოს ტრაპეციის დიაგონალების გადაკვეთის წერტილი Ა Ბ Გ Დსაფუძვლებით ძვ.წდა ახ.წ. ცნობილია, რომ სამკუთხედების ფართობები BOCდა AODთანაბარი შესაბამისად  და
და 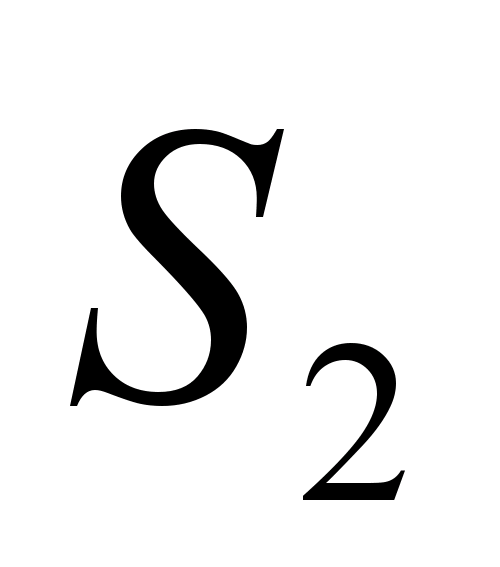 . იპოვნეთ ტრაპეციის ფართობი.
. იპოვნეთ ტრაპეციის ფართობი.
Kites აქვს რამდენიმე თვისება, რომელიც დაგვეხმარება ამოცნობა მათ სხვა quads. ფუტკრის დიაგონალები ხვდება მარჯვენა კუთხით. Kites აქვს ზუსტად ერთი წყვილი საპირისპირო კუთხეები, რომლებიც თანმიმდევრული. ეს ორი თვისება ილუსტრირებულია ქვემოთ მოცემულ დიაგრამაში.
ეს არის ჩვენი კონგრუენტური კუთხეების ერთადერთი წყვილი, რადგან? ნება მიეცით პრაქტიკას შეასრულოს ზოგიერთი პრობლემა, რომელიც მოითხოვს ტრაპეციისა და ფუტკრის თვისებების გამოყენებას, რომლის შესახებაც ახლა გავიგეთ. ვინაიდან მოცემულია ტრაპეციის ფუძის სიგრძეები, შეგვიძლია გავარკვიოთ რა უნდა იყოს შუა სეგმენტის სიგრძე. ამის გასარკვევად გამოვიყენოთ ფორმულა, რომელიც ჩვენ მივეცით შუა სეგმენტისთვის.
იმიტომ რომ . აქედან გამომდინარე, სამკუთხედების მსგავსებიდან ბშესახებCდა AODამას მოჰყვება 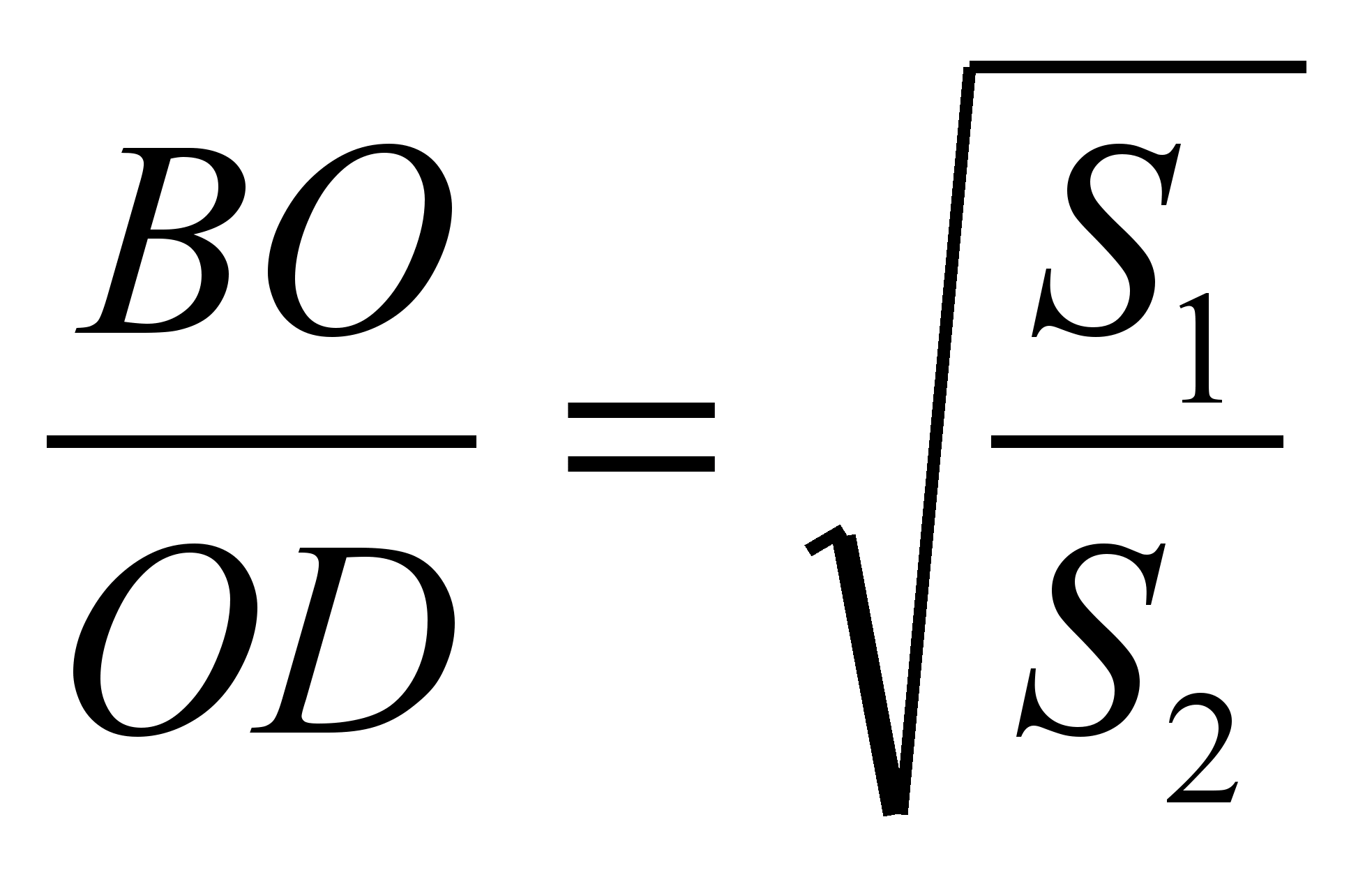 .აქედან გამომდინარე,
.აქედან გამომდინარე, 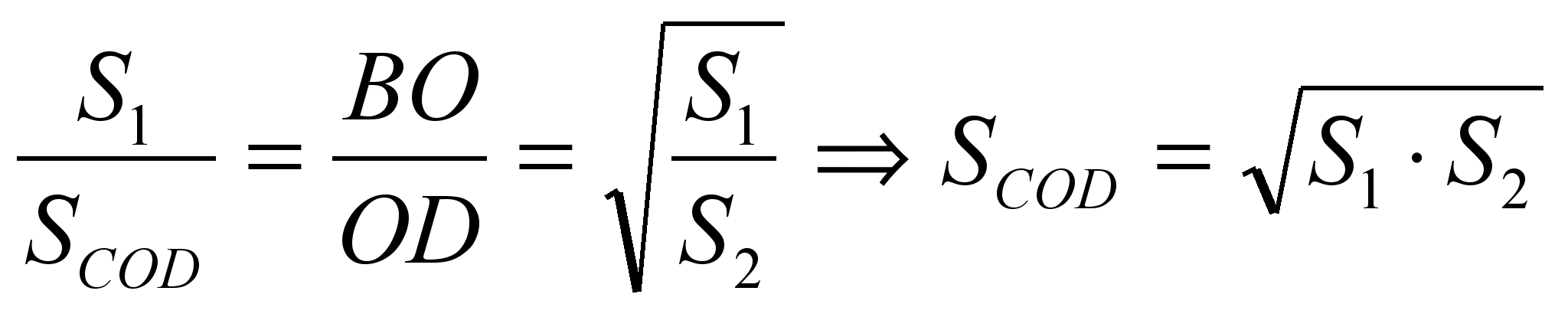 . მერე
. მერე
მსგავსების გამოყენებით შეიძლება ასევე დაამტკიცო სეგმენტის თვისება, რომელიც გადის ტრაპეციის დიაგონალების გადაკვეთის წერტილში ფუძეების პარალელურად. ვიწვევთ მოსწავლეებს ამოცანის გადასაჭრელად: „მოდით O იყოს ტრაპეციის დიაგონალების გადაკვეთის წერტილი. Ა Ბ Გ Დსაფუძვლებით ძვ.წდა ახ.წ. , . იპოვეთ სეგმენტის სიგრძე PKგადის ტრაპეციის დიაგონალების გადაკვეთის წერტილში ფუძეების პარალელურად. რა სეგმენტებად იყოფა? PKწერტილი შესახებ».
ნახატზე ჩვენ მხოლოდ ერთი კუთხის საზომი მოგვცეს, ამიტომ ამ ერთ ელემენტზე დაყრდნობით უნდა შეგვეძლოს მეტი ინფორმაციის დასკვნა. ვინაიდან ოთხკუთხედი არის ტოლფერდა ტრაპეცია, ვიცით, რომ ფუძის კუთხეები კონგრუენტულია. ახლა გავარკვიოთ რამდენი?
ერთად მათ აქვთ სულ 128°. გავიხსენოთ მრავალკუთხედის შიდა კუთხის თეორემა, რომ ოთხკუთხედის შიდა კუთხეები უნდა იყოს 360°. მოდით შევეცადოთ გამოვიყენოთ ეს ისე, რომ დაგვეხმაროს ღონისძიების განსაზღვრაში? ჯერ შევაჯამოთ ყველა კუთხე და დავაყენოთ 360°-ზე.
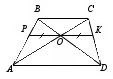
აქედან 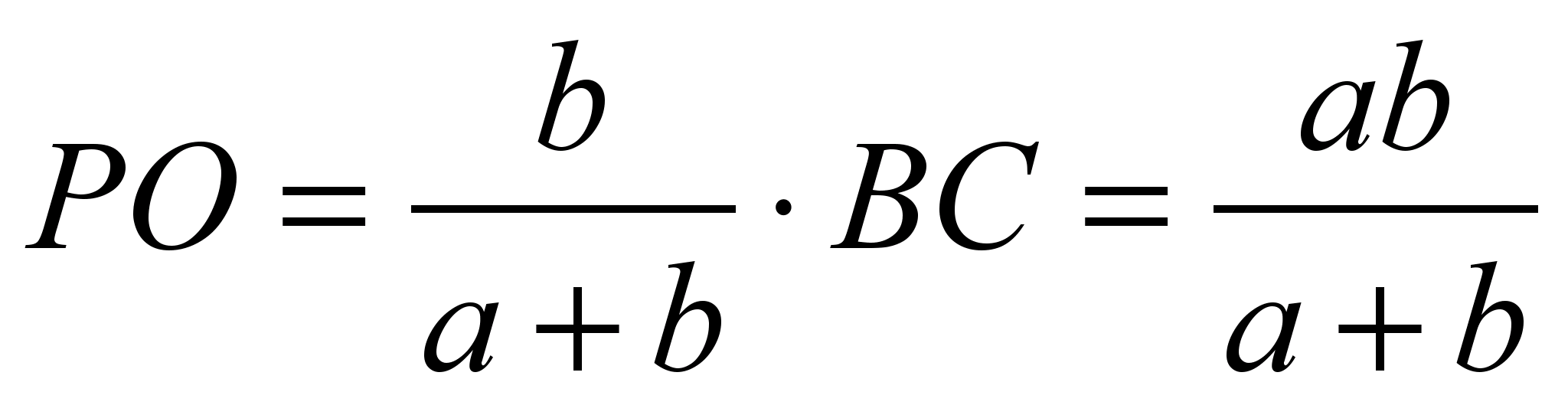 .
.
ანალოგიურად, სამკუთხედების მსგავსებიდან D.O.K.და DBC, ამას მოჰყვება 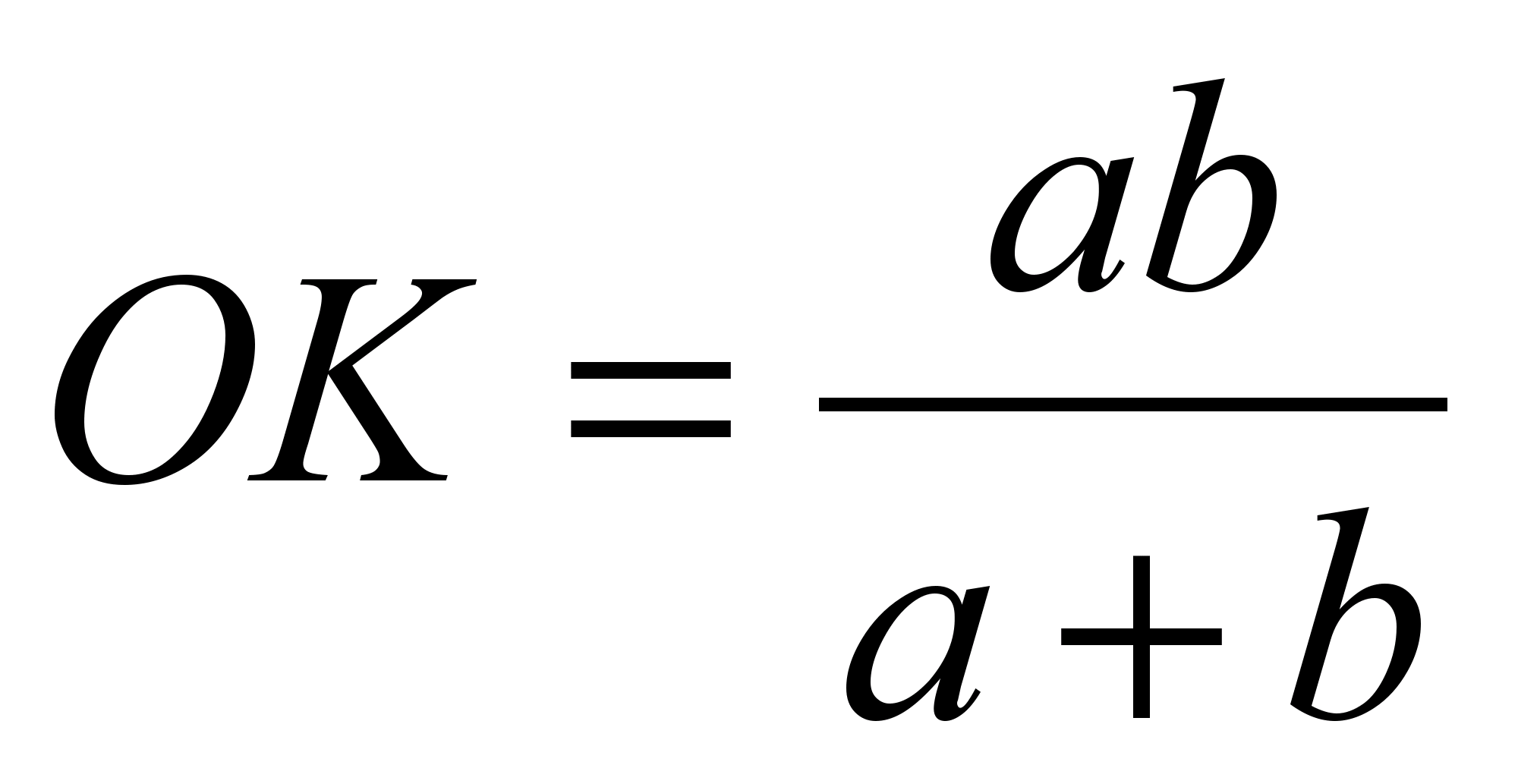 . აქედან
. აქედან 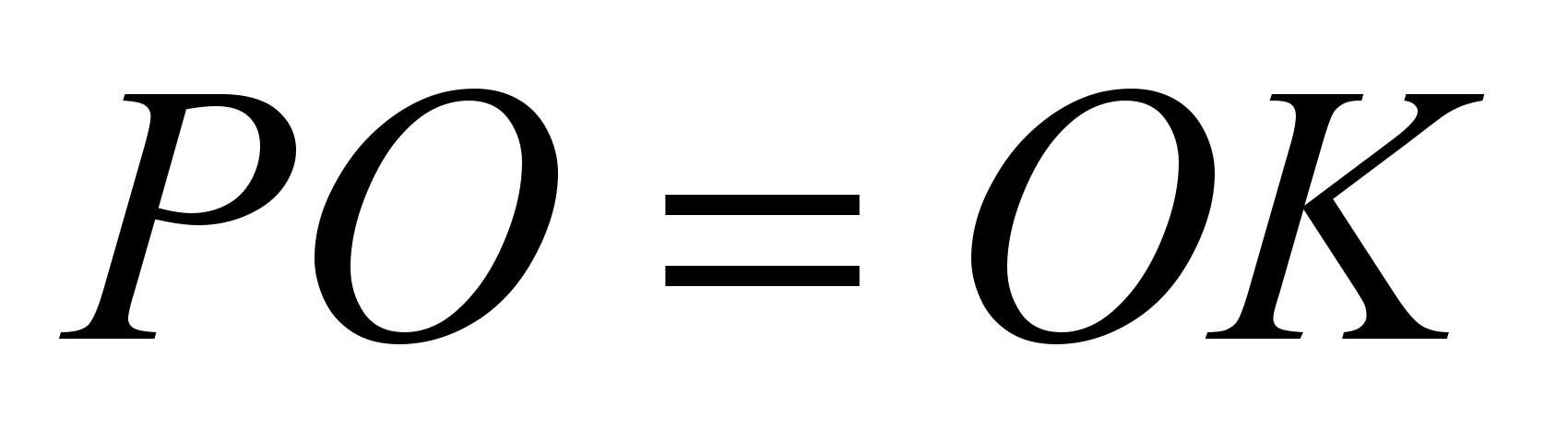 და
და 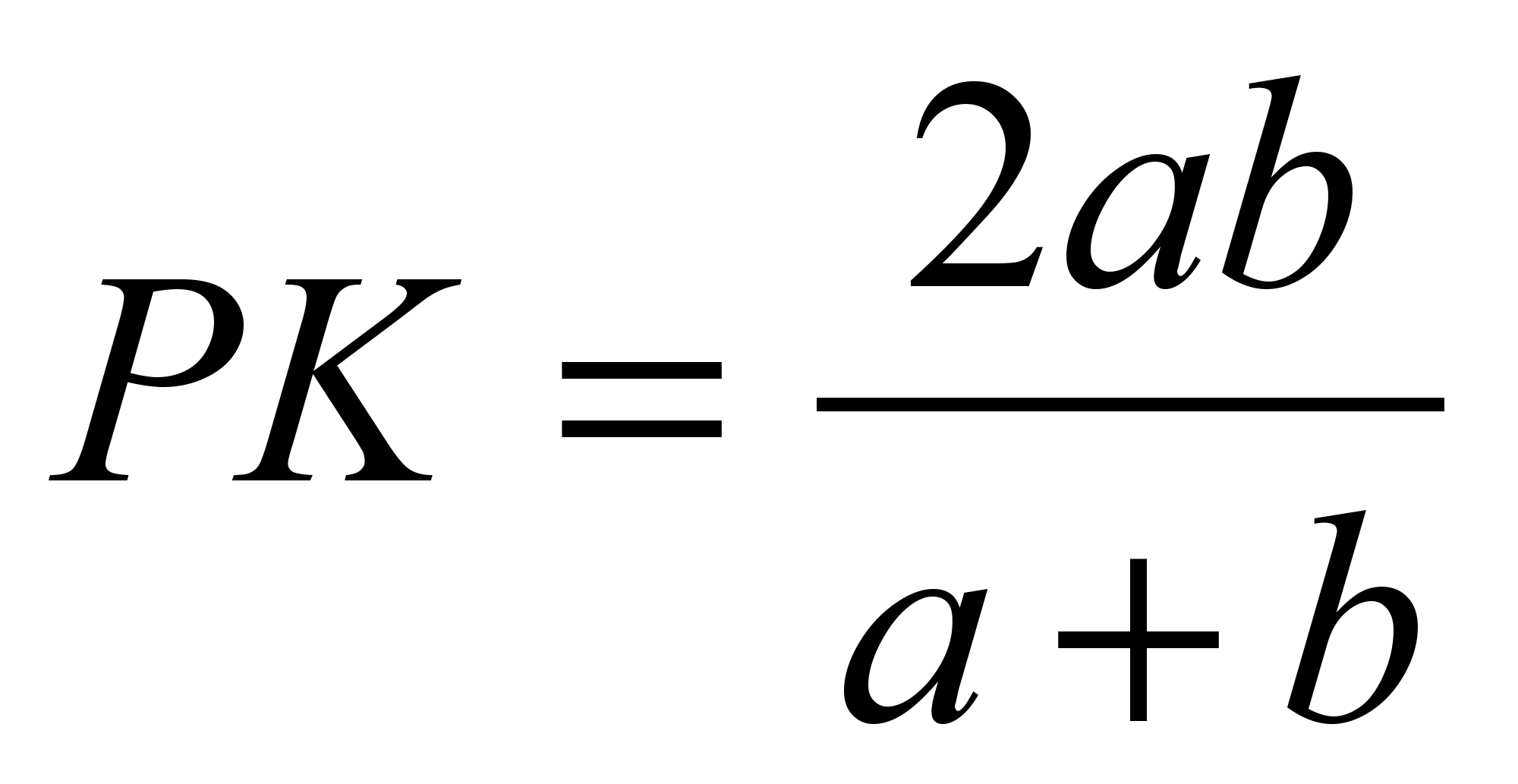 .
.
შემოხაზულია ტრაპეციის გარშემო
მაშ, თუ განვსაზღვრავთ ზომებს? ეს მნიშვნელობა ნიშნავს იმას, რომ ზომა? და ბოლოს, შეგვიძლია დავაყენოთ 116, რომ ტოლი იყოს? მიუხედავად იმისა, რომ ზემოაღნიშნული მეთოდი სავარჯიშოს ამოხსნის ღრმა გზა იყო, ჩვენ უბრალოდ შეგვეძლო გამოგვეყენებინა თვისება, რომ ტოლფერდა ტრაპეციის შემავსებელი კუთხეები ერთმანეთს ავსებენ. ამ გზით გადაჭრა ბევრად უფრო სწრაფია, რადგან ჩვენ მხოლოდ უნდა ვიპოვოთ რა არის 64° კომპლიმენტი.
როგორც კი ჩვენი პრობლემის ამ წერტილამდე მივალთ, უბრალოდ დავაყენებთ 116-ს 4-ზე და მოვაგვარებთ როგორც ადრე. ეს ჩვენც მოგვცეს? წარსულში, ჩვენ ვისწავლეთ რამდენიმე სამკუთხედის კონგრუენტობის თეორემა, რომელიც შეიძლება გამოვიყენოთ ამ სიტუაციაში, თუ ჩვენ შეგვიძლია ვიპოვოთ სხვა გვერდი ან კუთხე, რომელიც კონგრუენტულია.
მოსწავლეებს ვაცნობიერებთ დადასტურებულ თვისებას: ტრაპეციის ფუძეების პარალელური სეგმენტი, რომელიც გადის დიაგონალების გადაკვეთის წერტილში და აკავშირებს გვერდებზე ორ წერტილს, იყოფა დიაგონალების გადაკვეთის წერტილით შუაზე. მისი სიგრძე არის ტრაპეციის ფუძეების ჰარმონიული საშუალო.
შემდეგი საწყისი ოთხი პუნქტის თვისება:ტრაპეციაში დიაგონალების გადაკვეთის წერტილი, გვერდების გაგრძელების გადაკვეთის წერტილი, ტრაპეციის ფუძეების შუა წერტილები დევს იმავე ხაზზე.
ჩვენი ახალი ილუსტრაცია ნაჩვენებია ქვემოთ. ქვემოთ მოცემულია ამ სავარჯიშოს ორსვეტიანი გეომეტრიული მტკიცებულება. ისეთი გეომეტრიების წვდომისთვის, როგორიცაა. შეწყვიტე ბრძოლა და დაიწყე სწავლა დღესვე ათასობით უფასო რესურსით! თვისებები წარმოდგენილია შესაბამისი გაკვეთილების ბმულებით. გაკვეთილები ჩამოთვლილია ლოგიკური თანმიმდევრობით, რაც ნიშნავს, რომ თითოეული გაკვეთილი ეხება წინა გაკვეთილებს. და არ ეხება მას. სია აერთიანებს შესაბამის გაკვეთილებს, რომლებიც განთავსებულია სხვადასხვა გვერდებზეეს საიტი.
ტრაპეციის დიაგონალები და სიმაღლე
ტრაპეცია ტოლფერდაა, თუ და მხოლოდ მაშინ, თუ მისი ფუძის კუთხეები კონგრუენტულია. ტრაპეცია ტოლფერდაა, თუ და მხოლოდ მაშინ, თუ მისი ორი დიაგონალი თანმიმდევრულია. ტრაპეციის შუა ხაზი მისი ფუძეების პარალელურია. ტრაპეციის შუა ხაზის სიგრძე მისი ფუძეების სიგრძის ჯამის ნახევარია. ტრაპეციაში, გვერდითი მხარის შუა მხრიდან ფუძეების პარალელურად გამოყვანილი ხაზის მონაკვეთი კვეთს მეორე მხარეს მის შუა წერტილში.
გავაცნოთ მოსწავლეებს ფიგურების (არა სამკუთხედების) მსგავსებას, შეგვიძლია შევთავაზოთ იმ სეგმენტის სიგრძის პოვნა, რომელიც ყოფს ტრაპეციას ორ მსგავსებად.
ამრიგად, სეგმენტს, რომელიც ყოფს ტრაპეციას ორ მსგავს ტრაპეციად, აქვს სიგრძე ფუძეების სიგრძის საშუალო გეომეტრიულ საშუალოს.
ტრაპეციის ფართობის ფორმულის გამოყვანის შემდეგ, სასარგებლოა დამტკიცება სეგმენტის თვისება, რომელიც ყოფს ტრაპეციას ორ თანაბარ ნაწილად.
ტრაპეციის შუა ხაზი არის ტრაპეციის ფუძეების შემცველი ორი სწორი ხაზისგან თანაბრად დაშორებული წერტილების ადგილი. ტრაპეციაში გვერდითი მხარის ბოლოებში შიდა კუთხეების ჯამი არის 180°. ტრაპეციაში შუა ხაზი ყოფს ხაზების ნებისმიერ სეგმენტს, რომელიც აკავშირებს უფრო მოკლე ფუძეზე არსებულ წერტილს უფრო დიდ ფუძეზე. ტრაპეციაში, მისი დიაგონალების შუა წერტილებს შორის მანძილი არის უფრო დიდი და მოკლე ფუძეების სიგრძის სხვაობის ნახევარი.
თუ ტრაპეციაში ორი მოპირდაპირე შიდა კუთხის ჯამი არის 180°, მაშინ ტრაპეცია ტოლფერდაა. ტოლფერდა ტრაპეციაში ფუძეების პარალელურად დიაგონალურ კვეთაზე გამავალი ხაზი ყოფს დიაგონალებს შორის არსებულ კუთხეს. ტოლფერდა ტრაპეციაში, გვერდითი მხარე ჩანს ერთი კუთხით ორი საპირისპირო წვეროდან.
მოდით შევქმნათ სისტემა 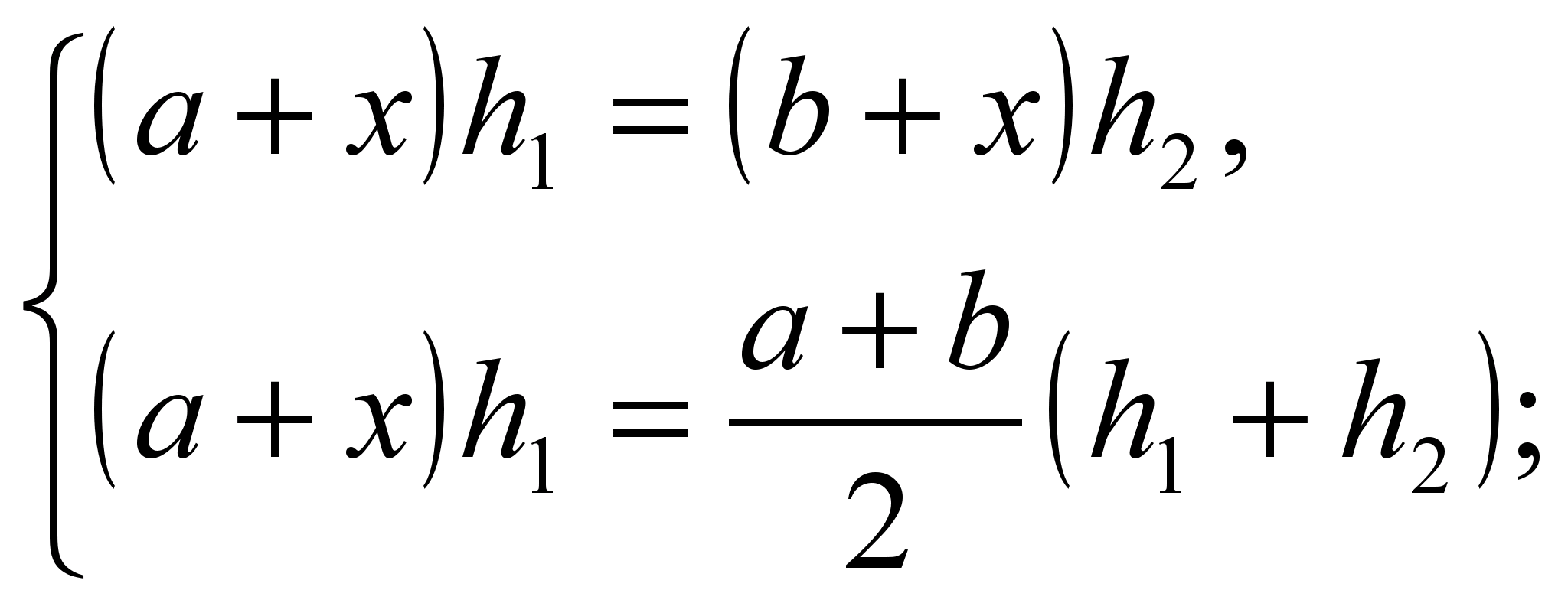
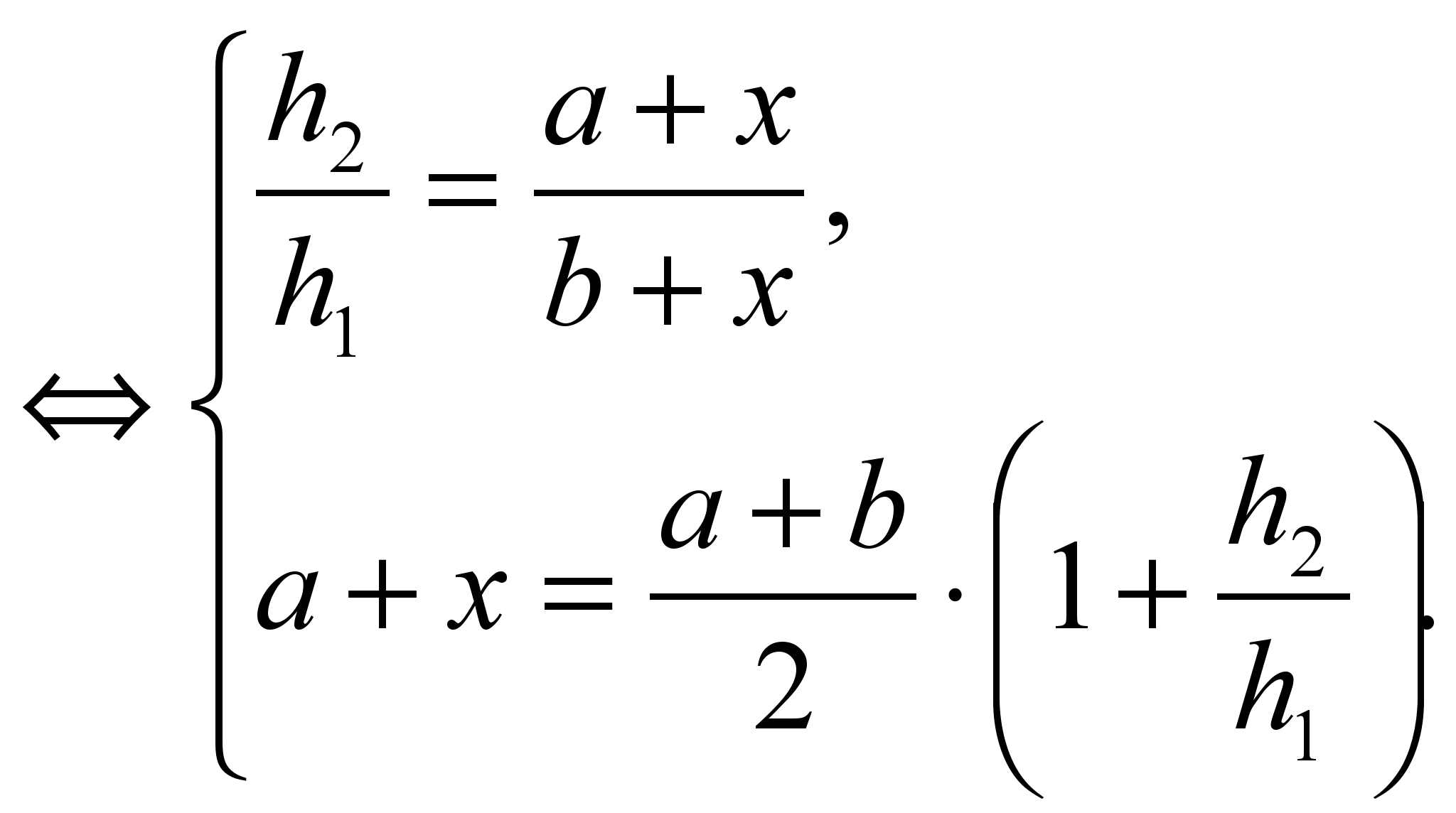
სისტემის გადაწყვეტა 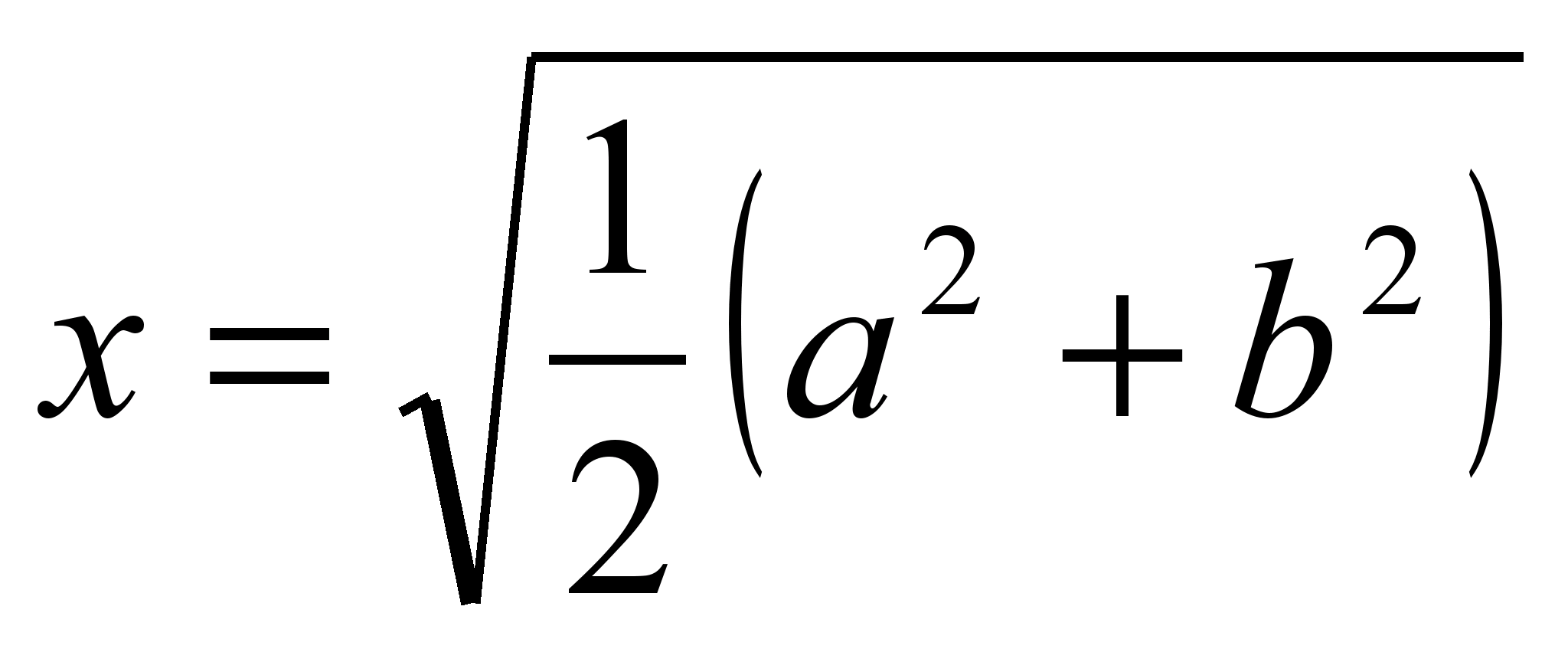 .
.
ამრიგად, ტრაპეციის ორ თანაბარ ნაწილად გამყოფი სეგმენტის სიგრძე უდრის 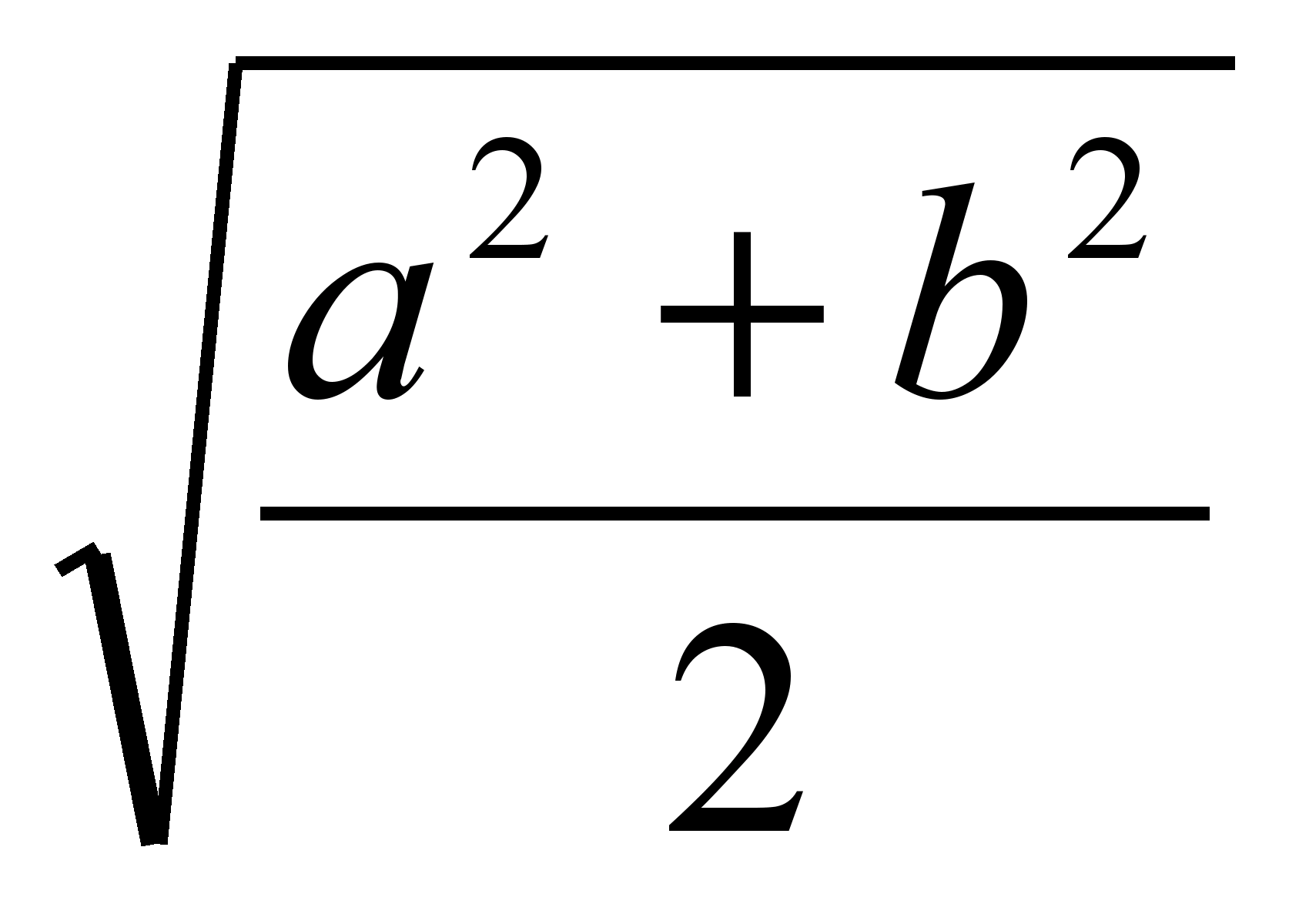 (ძირის საშუალო კვადრატული სიგრძე).
).
(ძირის საშუალო კვადრატული სიგრძე).
).
გაკვეთილების სია ახლა იგივეა, რაც მოკლე შეჯამება. ტოლფეროვან ტრაპეციაში ფუძის კუთხეები კონგრუენტულია. თეორემა 2. თუ ტრაპეციის ფუძის კუთხეები თანმიმდევრულია, მაშინ ტრაპეცია ტოლფერდაა. ამოჭრილი ამოცანები ტოლკუთხა ტრაპეციაში ფუძის კუთხე არის 73°. იპოვეთ ტრაპეციის ყველა სხვა კუთხე. ტოლფერდა ტრაპეციაში ფუძის კუთხე სამჯერ აღემატება შიდა კუთხეს მოკლე ფუძის ბოლოს. იპოვეთ ტრაპეციის ყველა კუთხე.
ტრაპეციაში ფუძეების პარალელურად გვერდის შუა ნაწილიდან გამოყვანილი ხაზის სეგმენტი კვეთს მეორე მხარეს მის შუა წერტილში. იპოვეთ ტრაპეციის სიგრძე შუა ხაზზე. ტრაპეციაში დიდი ფუძე 27 სმ სიგრძისაა და ძირზე 10 სმ-ით გრძელია.
იმისათვის, რომ მოსწავლეებმა გააცნობიერონ მითითებულ სეგმენტებს შორის კავშირი, მათ უნდა სთხოვონ ააგონ ისინი მოცემული ტრაპეციისთვის. მოსწავლეები სირთულის გარეშე ააშენებენ ტრაპეციის შუა ხაზს და ტრაპეციის დიაგონალების გადაკვეთის წერტილს ფუძეების პარალელურად გამავალ სეგმენტს. სად იქნება მესამე და მეოთხე სეგმენტები? ამ კითხვაზე პასუხმა უნდა მიიყვანოს მოსწავლეები საშუალო მაჩვენებლებს შორის კავშირის აღმოჩენაში.
იპოვეთ ტრაპეციის ფუძეების სიგრძე. ტოლფერდა ტრაპეციაში ორი დიაგონალი თანმიმდევრულია. ამოცანა 2. თუ ტრაპეციაში ორი დიაგონალი თანმიმდევრულია, მაშინ ტრაპეცია ტოლფერდაა. ამოცანა 3. ტრაპეციის შუა ხაზის ნებისმიერი წერტილი თანაბრად არის დაშორებული ტრაპეციის ფუძეების შემცველი ორი პარალელური ხაზისგან. თუ სიბრტყის წერტილი თანაბრად არის დაშორებული ორი პარალელური ხაზისგან, რომლებიც შეიცავს ტრაპეციის ფუძეებს, მაშინ წერტილი ეკუთვნის წრფეს, რომელიც შეიცავს. ტრაპეცია შუა ხაზზე. მოგვარებული პრობლემა. ტრაპეციაში, სწორი ხაზის ნებისმიერი სეგმენტი, რომელიც აკავშირებს უფრო მოკლე ფუძის წერტილს უფრო დიდი ფუძის წერტილთან, ორად არის დანაწევრებული ტრაპეციის შუა ხაზზე.
ჩაწერილი და შემოხაზული ოთხკუთხედის ატრიბუტი და თვისება უნდა იყოს მითითებული სტუდენტებისთვის ცნობილი ყველა ოთხკუთხედისთვის, ტრაპეციის ჩათვლით.
აღწერილი ტრაპეციის თვისებები.ტრაპეცია შეიძლება აღწერილი იყოს წრის შესახებ, თუ და მხოლოდ იმ შემთხვევაში, თუ ფუძეების სიგრძის ჯამი ტოლია გვერდების სიგრძის ჯამს.
პირველი აშკარაა. მეორე დასკვნის დასამტკიცებლად აუცილებელია დადგინდეს, რომ კუთხე CODპირდაპირი, რაც ასევე არ არის დიდი საქმე. მაგრამ ამ შედეგის ცოდნა საშუალებას გვაძლევს გამოვიყენოთ მართკუთხა სამკუთხედი პრობლემების გადასაჭრელად.
ტრაპეციაში გვერდითი მხარის ბოლოებში შიდა კუთხეების ბისექტრები სწორი კუთხით იკვეთება. ტრაპეციაში, გვერდითი მხარის ბოლოებში შიდა კუთხეების ბისექტრები იკვეთება ტრაპეციის შუა ხაზზე მდებარე წერტილში. ამოცანა 4. ტოლფერდა ტრაპეციაში ფუძის კუთხე არის 60 °. დაამტკიცეთ, რომ უფრო მოკლე ფუძის სიგრძე უდრის სხვაობას უფრო გრძელი ფუძის სიგრძესა და გვერდითი მხარის სიგრძეს შორის.
ტოლფერდა ტრაპეციაში დიაგონალი არის 10 სმ და 60° ფუძესთან. იპოვეთ საშუალო სიგრძის ტრაპეციის სიგრძე. ტრაპეციის ფუძეები 3 და 5 ერთეულის სიგრძისაა, ერთი დიაგონალი გვერდის პერპენდიკულარულია, ხოლო მეორე დიაგონალი ორად ყოფს კუთხეს. უფრო დიდ ბაზაზე. იპოვეთ ტრაპეციის სიმაღლე. სახაზავი და კომპასის გამოყენებით ააგეთ ტრაპეცია, რომელსაც აქვს ფუძეები, რომლებიც ემთხვევა მოცემულ ორ სეგმენტს და მხარეები, კონგრუენტული. ორი სხვა მოცემული სეგმენტი.
მოდით დავაკონკრეტოთ შედეგები ტოლფერდა შემოხაზული ტრაპეცია :
|
|
ტოლფერდა შემოხაზული ტოლფერდა ტრაპეციის სიმაღლე არის ტრაპეციის ფუძეების გეომეტრიული საშუალო. ტრაპეციის დიაგონალები და კუთხეებისახაზავი და კომპასის გამოყენებით ააგეთ ტრაპეცია, რომელსაც აქვს ფუძეები, რომლებიც ემთხვევა მოცემულ ორ სეგმენტს და გვერდს, რომლებიც კონგრუენტია. ორ სხვა მოცემულ სეგმენტზე. გეომეტრია არის მათემატიკის სპეციფიკური საგანი, რომელიც ეხება ფორმებსა და ობიექტებს და მათთან დაკავშირებულ პრობლემებს. არსებობს განსხვავებული ტიპები გეომეტრიული ფორმები. რამდენიმე მნიშვნელოვანი 2D ფორმაა კვადრატი, მართკუთხედი, სამკუთხედი, მრავალკუთხედი, წრე, პარალელოგრამი, ტრაპეცია, რომბი და ა.შ. ოთხი გვერდით შემოზღუდულ ფორმას ოთხკუთხედი ეწოდება. |
განვიხილოთ ტრაპეციის თვისებების შესწავლის მეთოდოლოგიის ძირითადი პრინციპები.
პირველი, ეს არის გამოყენება დავალების მიდგომა . არ არის საჭირო ტრაპეციის ახალი თვისებების შეტანა გეომეტრიის თეორიულ კურსში. ამ თვისებებს მოსწავლეები აღმოაჩენენ და აყალიბებენ პრობლემის გადაჭრის გზით (უკეთესია, ვიდრე პრობლემური სისტემები). მნიშვნელოვანია, რომ მასწავლებელმა იცოდეს, რა ამოცანები უნდა დაისვას სასწავლო პროცესის რომელ ეტაპზე. გარდა ამისა, თითოეული თვისება შეიძლება იყოს ძირითადი ამოცანა ამოცანების სისტემაში.
Მეორეც, ტრაპეციის თვისებების შესწავლის "სპირალური" ორგანიზაცია
. შეგიძლიათ რამდენჯერმე დაუბრუნდეთ ინდივიდუალურ თვისებებს, მაშინ, სავარაუდოდ, სტუდენტები დაიმახსოვრებენ მათ. მაგალითად, ოთხი წერტილის თვისება შეიძლება დადასტურდეს მსგავსების შესწავლით და შემდეგ ვექტორების გამოყენებით. ტრაპეციის გვერდების მიმდებარე სამკუთხედების თანაბარი ფართობი შეიძლება დადასტურდეს სამკუთხედების თვისებად. თანაბარი სიმაღლეებიერთ სწორ ხაზზე დაწოლილ გვერდებზე დახატული და ფორმულა 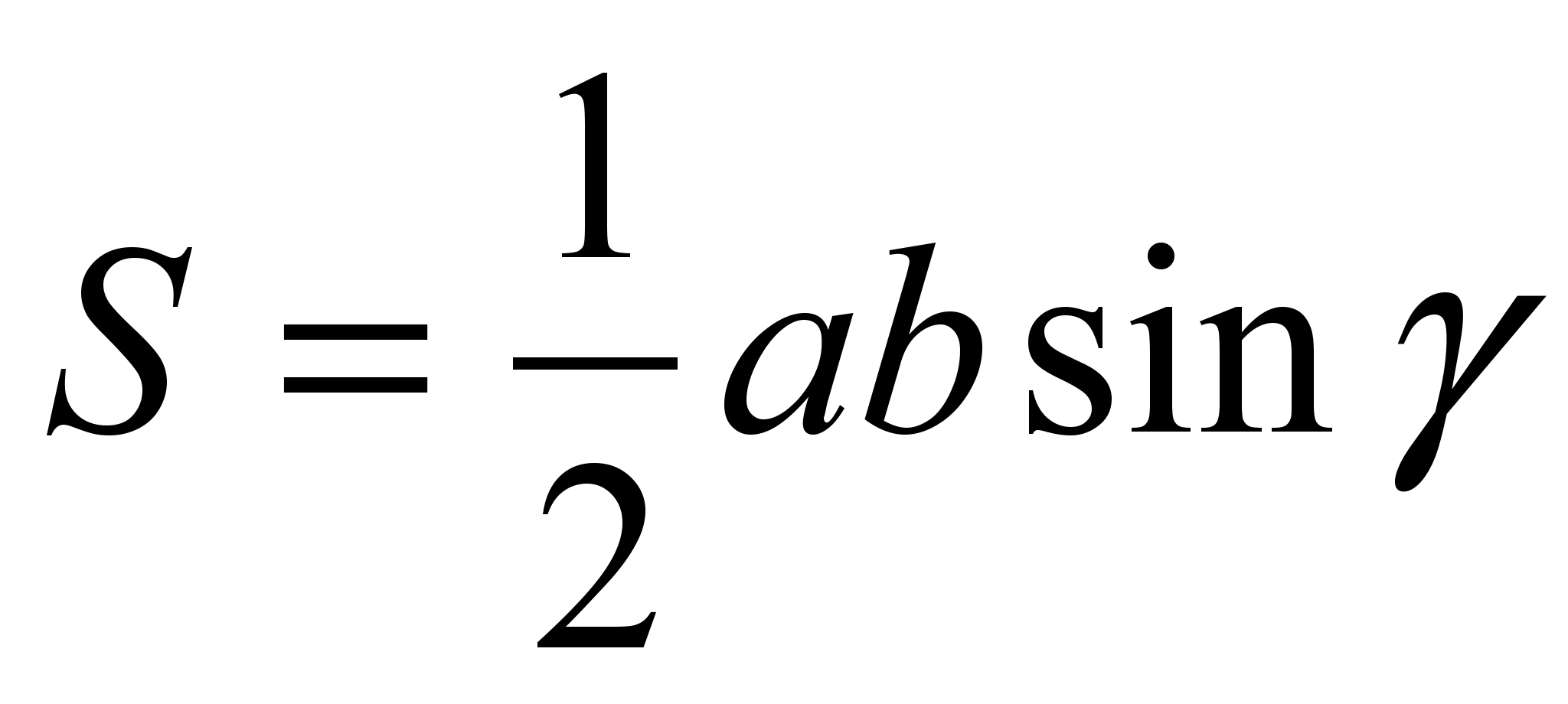 . თქვენ შეგიძლიათ შეიმუშაოთ მართკუთხა სამკუთხედის თვისებები შემოხაზულ ტრაპეციაზე, სინუსების თეორემა შემოხაზულ ტრაპეციაზე და ა.შ.
. თქვენ შეგიძლიათ შეიმუშაოთ მართკუთხა სამკუთხედის თვისებები შემოხაზულ ტრაპეციაზე, სინუსების თეორემა შემოხაზულ ტრაპეციაზე და ა.შ.
ტრაპეციის "არაპროგრამული" თვისებების შემოთავაზებული ჩართვა სასკოლო გეომეტრიის კურსის შინაარსში, მათი შესწავლის დავალების ტექნოლოგია, ტრაპეციის თვისებების განმეორებითი მითითება სხვა თემების შესწავლისას საშუალებას მისცემს სტუდენტებს უფრო ღრმად გაიგონ ტრაპეცია. და უზრუნველყოს პრობლემების გადაჭრის წარმატება მისი თვისებების გამოყენებასთან დაკავშირებით.
ამიტომ, ერთ-ერთ მათგანს დავარქმევთ დიდი
, მეორე - პატარა ბაზა
ტრაპეცია. სიმაღლე
ტრაპეცია შეიძლება ეწოდოს პერპენდიკულარის ნებისმიერ სეგმენტს, რომელიც შედგენილია წვეროებიდან შესაბამის მოპირდაპირე მხარეს (თითოეული წვეროსთვის არის ორი საპირისპირო მხარე), ჩასმული აღებულ წვეროსა და მოპირდაპირე მხარეს შორის. მაგრამ შეიძლება გამოვყოთ განსაკუთრებული სახის"სიმაღლეები.
განმარტება 8.
ტრაპეციის ფუძის სიმაღლე არის ფუძეებზე პერპენდიკულარული სწორი ხაზის სეგმენტი, რომელიც ჩასმულია ფუძეებს შორის.
თეორემა 7
. ტრაპეციის მედიანური ხაზი ფუძეების პარალელურია და მათი ჯამის ნახევარს უდრის.
მტკიცებულება. მიეცით ტრაპეცია ABCD და მედიანა ხაზი KM. გაავლეთ ხაზი B და M წერტილებს შორის. ჩვენ ვაგრძელებთ AD მხარეს D წერტილის გავლით, სანამ არ გადაიკვეთება BM-სთან. სამკუთხედები BCm და MPD ტოლია გვერდით და ორი კუთხით (CM=MD, ∠ BCM=∠ MDP - გადახურვა, ∠ BMC=∠ DMP - ვერტიკალური), ამიტომ VM=MP ან წერტილი M არის BP-ის შუა წერტილი. KM არის შუა ხაზი სამკუთხედში ABP. სამკუთხედის შუა ხაზის თვისების მიხედვით, KM პარალელურია AP-ის და კერძოდ AD-ის და უდრის AP-ის ნახევარს: 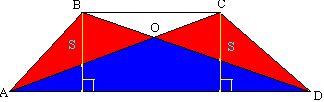 თეორემა 8
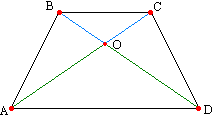
. დიაგონალები ყოფს ტრაპეციას ოთხ ნაწილად, რომელთაგან ორი, გვერდების მიმდებარედ, ტოლია.
თეორემა 8
. დიაგონალები ყოფს ტრაპეციას ოთხ ნაწილად, რომელთაგან ორი, გვერდების მიმდებარედ, ტოლია.
შეგახსენებთ, რომ ფიგურებს ტოლი ეწოდება, თუ მათ აქვთ იგივე ფართობი. სამკუთხედები ABD და ACD ტოლია: მათ აქვთ თანაბარი სიმაღლეები (მითითებულია ყვითლად) და საერთო ფუძე. ამ სამკუთხედებს აქვთ საერთო ნაწილი AOD. მათი არეალის გაფართოება შესაძლებელია შემდეგნაირად: 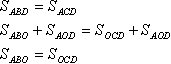
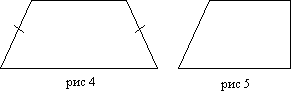 ტრაპეციის სახეები:
ტრაპეციის სახეები:
განმარტება 9.
(სურათი 1) მახვილკუთხა ტრაპეცია არის ტრაპეცია, რომელშიც უფრო დიდი ფუძის მიმდებარე კუთხეები მწვავეა.
განმარტება 10.
(სურათი 2) ბლაგვი ტრაპეცია არის ტრაპეცია, რომელშიც უფრო დიდი ფუძის მიმდებარე კუთხე ბლაგვია.
განმარტება 11.
(სურათი 4) ტრაპეციას მართკუთხა ეწოდება, რომლის ერთი მხარე ფუძეების პერპენდიკულარულია.
განმარტება 12.
(სურათი 3) ტოლკუთხედი (იზოლა, ტოლფერდა) არის ტრაპეცია, რომელშიც გვერდები ტოლია.
 ტოლფერდა ტრაპეციის თვისებები:
ტოლფერდა ტრაპეციის თვისებები:
თეორემა 10
. ტოლფერდა ტრაპეციის თითოეული ფუძის მიმდებარე კუთხეები ტოლია.
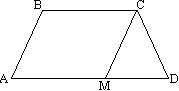
მტკიცებულება. მოდით დავამტკიცოთ, მაგალითად, A და D კუთხეების ტოლობა ABCD ტოლფერდა ტრაპეციის უფრო დიდი AD ფუძით. ამ მიზნით ვხაზავთ სწორ ხაზს C წერტილის გავლით გვერდითი AB მხარის პარალელურად. ის გადაკვეთს დიდ ფუძეს M წერტილში. ოთხკუთხედი ABCM არის პარალელოგრამი, რადგან კონსტრუქციით მას აქვს ორი წყვილი პარალელური გვერდი. მაშასადამე, ტრაპეციის შიგნით ჩასმული სექციური ხაზის CM სეგმენტი უდრის მის გვერდით მხარეს: CM=AB. აქედან ირკვევა, რომ CM=CD, სამკუთხედი CMD არის ორკუთხედი, ∠CMD=∠CDM და, შესაბამისად, ∠A=∠D. პატარა ფუძის მიმდებარე კუთხეებიც ტოლია, რადგან არის მათთვის, ვინც ნაპოვნია შიდა ცალმხრივი და აქვს ორი ხაზის ჯამი. 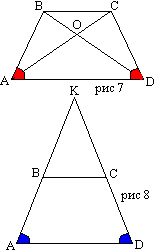 თეორემა 11
. ტოლფერდა ტრაპეციის დიაგონალები ტოლია.
თეორემა 11
. ტოლფერდა ტრაპეციის დიაგონალები ტოლია.
მტკიცებულება. განვიხილოთ სამკუთხედები ABD და ACD. ის ტოლია ორ მხარეს და მათ შორის კუთხეს (AB=CD, AD საერთოა, A და D კუთხეები ტოლია თეორემა 10-ის მიხედვით). ამიტომ AC=BD.
 თეორემა 13
. ტოლფერდა ტრაპეციის დიაგონალები გადაკვეთის წერტილით იყოფა შესაბამის ტოლ სეგმენტებად. განვიხილოთ სამკუთხედები ABD და ACD. ის ტოლია ორ მხარეს და მათ შორის კუთხეს (AB=CD, AD საერთოა, A და D კუთხეები ტოლია თეორემა 10-ის მიხედვით). მაშასადამე, ∠ ОАD=∠ ОDA, მაშასადამე, კუთხეები ОВС და OSV ტოლია, როგორც შესაბამისად გადაფარვის კუთხეები ODA და OAD. გავიხსენოთ თეორემა: თუ სამკუთხედში ორი კუთხე ტოლია, მაშინ ის ტოლფერდაა, ამიტომ სამკუთხედები ОВС და ОAD არის ტოლი, რაც ნიშნავს OS=OB და ОА=OD და ა.შ.
თეორემა 13
. ტოლფერდა ტრაპეციის დიაგონალები გადაკვეთის წერტილით იყოფა შესაბამის ტოლ სეგმენტებად. განვიხილოთ სამკუთხედები ABD და ACD. ის ტოლია ორ მხარეს და მათ შორის კუთხეს (AB=CD, AD საერთოა, A და D კუთხეები ტოლია თეორემა 10-ის მიხედვით). მაშასადამე, ∠ ОАD=∠ ОDA, მაშასადამე, კუთხეები ОВС და OSV ტოლია, როგორც შესაბამისად გადაფარვის კუთხეები ODA და OAD. გავიხსენოთ თეორემა: თუ სამკუთხედში ორი კუთხე ტოლია, მაშინ ის ტოლფერდაა, ამიტომ სამკუთხედები ОВС და ОAD არის ტოლი, რაც ნიშნავს OS=OB და ОА=OD და ა.შ.
ტოლფერდა ტრაპეცია არის სიმეტრიული ფიგურა.
განმარტება 13.
ტოლფერდა ტრაპეციის სიმეტრიის ღერძს ეწოდება სწორი ხაზი, რომელიც გადის მისი ფუძის შუა წერტილებში.
თეორემა 14
. ტოლფერდა ტრაპეციის სიმეტრიის ღერძი პერპენდიკულარულია მის ფუძეებზე. 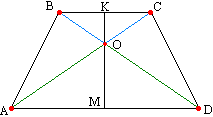 მე-9 თეორემაში დავამტკიცეთ, რომ ტრაპეციის ფუძეების შუა წერტილებთან შემაერთებელი ხაზი დიაგონალების გადაკვეთის წერტილში გადის. შემდეგ (თეორემა 13) დავამტკიცეთ, რომ სამკუთხედები AOD და BOC ტოლფერდაა. OM და OK არის ამ სამკუთხედების მედიანა, შესაბამისად, განსაზღვრებით. გავიხსენოთ ტოლფერდა სამკუთხედის თვისება: ტოლფერდა სამკუთხედის მედიანა, რომელიც ძირამდეა დაშვებული, ასევე არის სამკუთხედის სიმაღლე. სწორი ხაზის ნაწილების ფუძეების პერპენდიკულარულობის გამო KM სიმეტრიის ღერძი პერპენდიკულარულია ფუძეებზე.
მე-9 თეორემაში დავამტკიცეთ, რომ ტრაპეციის ფუძეების შუა წერტილებთან შემაერთებელი ხაზი დიაგონალების გადაკვეთის წერტილში გადის. შემდეგ (თეორემა 13) დავამტკიცეთ, რომ სამკუთხედები AOD და BOC ტოლფერდაა. OM და OK არის ამ სამკუთხედების მედიანა, შესაბამისად, განსაზღვრებით. გავიხსენოთ ტოლფერდა სამკუთხედის თვისება: ტოლფერდა სამკუთხედის მედიანა, რომელიც ძირამდეა დაშვებული, ასევე არის სამკუთხედის სიმაღლე. სწორი ხაზის ნაწილების ფუძეების პერპენდიკულარულობის გამო KM სიმეტრიის ღერძი პერპენდიკულარულია ფუძეებზე.
ნიშნები, რომლებიც განასხვავებენ ტოლფეროვან ტრაპეციას ყველა ტრაპეციას შორის:
თეორემა 15
. თუ ტრაპეციის ერთ-ერთი ფუძის მიმდებარე კუთხეები ტოლია, მაშინ ტრაპეცია ტოლფერდაა.
თეორემა 16
. თუ ტრაპეციის დიაგონალები ტოლია, მაშინ ტრაპეცია ტოლფერდაა.
თეორემა 17
. თუ ტრაპეციის გვერდითი მხარეები, რომლებიც გადაკვეთაზეა გადაჭიმული, მის დიდ ფუძესთან ერთად ქმნის ტოლფერდა სამკუთხედს, მაშინ ტრაპეცია არის ტოლფერდა.
თეორემა 18
. თუ ტრაპეცია შეიძლება ჩაიწეროს წრეში, მაშინ ის არის ტოლფერდა.
მართკუთხა ტრაპეციის ნიშანი:
თეორემა 19
. ნებისმიერი ოთხკუთხედი, რომელსაც მხოლოდ ორი მართი კუთხე აქვს მიმდებარე წვეროებზე, არის მართკუთხა ტრაპეცია (აშკარაა, რომ ორი გვერდი პარალელურია, რადგან ცალმხრივი ტოლია. იმ შემთხვევაში, როდესაც სამი მართკუთხედია მართკუთხედი)
თეორემა 20
. ტრაპეციაში ჩაწერილი წრის რადიუსი უდრის ფუძის სიმაღლის ნახევარს. 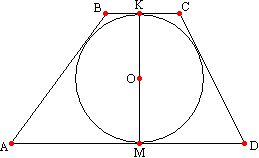 ამ თეორემის დასტურია იმის ახსნა, რომ ფუძეებისკენ მიზიდული რადიუსი მდებარეობს ტრაპეციის სიმაღლეზე. O წერტილიდან - ამ ტრაპეციაში ჩაწერილი ABCD წრის ცენტრიდან, ვხატავთ რადიუსებს ტრაპეციის მის ფუძეებთან შეხების წერტილებამდე. მოგეხსენებათ, შეხების წერტილთან მიყვანილი რადიუსი ტანგენტის პერპენდიკულარულია, ამიტომ OK ^ BC და OM ^ AD. გავიხსენოთ თეორემა: თუ წრფე პერპენდიკულარულია ერთ-ერთ პარალელურ წრფეზე, მაშინ ის ასევე პერპენდიკულარულია მეორეზე. აქედან გამომდინარე, ხაზი OK ასევე პერპენდიკულარულია AD-ზე. ამრიგად, AD წრფეზე პერპენდიკულარული ორი წრფე გადის O წერტილში, რომელიც არ შეიძლება იყოს, ამიტომ ეს წრფეები ემთხვევა და ქმნიან საერთო პერპენდიკულარულ KM-ს, რომელიც უდრის ორი რადიუსის ჯამს და არის ჩაწერილი წრის დიამეტრი. r=KM/2 ან r=h/2.
ამ თეორემის დასტურია იმის ახსნა, რომ ფუძეებისკენ მიზიდული რადიუსი მდებარეობს ტრაპეციის სიმაღლეზე. O წერტილიდან - ამ ტრაპეციაში ჩაწერილი ABCD წრის ცენტრიდან, ვხატავთ რადიუსებს ტრაპეციის მის ფუძეებთან შეხების წერტილებამდე. მოგეხსენებათ, შეხების წერტილთან მიყვანილი რადიუსი ტანგენტის პერპენდიკულარულია, ამიტომ OK ^ BC და OM ^ AD. გავიხსენოთ თეორემა: თუ წრფე პერპენდიკულარულია ერთ-ერთ პარალელურ წრფეზე, მაშინ ის ასევე პერპენდიკულარულია მეორეზე. აქედან გამომდინარე, ხაზი OK ასევე პერპენდიკულარულია AD-ზე. ამრიგად, AD წრფეზე პერპენდიკულარული ორი წრფე გადის O წერტილში, რომელიც არ შეიძლება იყოს, ამიტომ ეს წრფეები ემთხვევა და ქმნიან საერთო პერპენდიკულარულ KM-ს, რომელიც უდრის ორი რადიუსის ჯამს და არის ჩაწერილი წრის დიამეტრი. r=KM/2 ან r=h/2.
თეორემა 21
. ტრაპეციის ფართობი ტოლია ფუძეების ჯამის ნახევრის ნამრავლისა და ფუძეების სიმაღლისა. 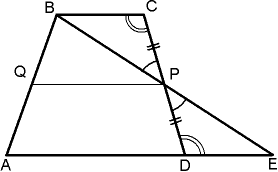
მტკიცებულება:მოდით ABCD იყოს მოცემული ტრაპეცია და AB და CD იყოს მისი ფუძეები. მოდით ასევე AH იყოს A წერტილიდან CD წრფეზე ჩამოშვებული სიმაღლე. შემდეგ S ABCD = S ACD + S ABC.
მაგრამ S ACD = 1/2AH CD და S ABC = 1/2AH AB.
ამიტომ, S ABCD = 1/2AH (AB + CD).
ქ.ე.დ.
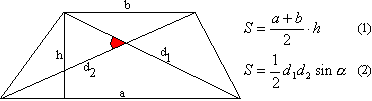 მეორე ფორმულა გადავიდა ოთხკუთხედიდან.
მეორე ფორმულა გადავიდა ოთხკუთხედიდან.
შეიძლება სასარგებლო იყოს წაკითხვა:
- მკურნალობა საზღვარგარეთ. ნუ გეშინია. საზღვარგარეთ მკურნალობა - სამედიცინო ტურიზმის ძირითადი მიმართულებები საზღვარგარეთ მკურნალობა სად ჯობია;
- კითხვა მაქვს: როგორ მოვიშორო სტრესი;
- მთავარი ტრაგედიები Romina Power Albano Carrisi ბავშვების ცხოვრებაში რას აკეთებენ ისინი;
- რა უნდა გააკეთოს, თუ ბავშვს არ სურს საბავშვო ბაღში მეგობრობა;
- ქინძი - სასარგებლო თვისებები და გამოყენება ქინძის ეთერზეთი კოსმეტოლოგიაში;
- კლასიკური ვინეგრეტი მჟავე კომბოსტოთი - ეტაპობრივი რეცეპტი ფოტოთი;
- ჯანსაღ სხეულში ჯანსაღი გონება?;
- პენსიონერის სამსახურიდან გათავისუფლების პროცედურა: არსებული საფუძველი და შეზღუდვები და როგორ შეგიძლიათ დაიცვათ თქვენი უფლებები?;
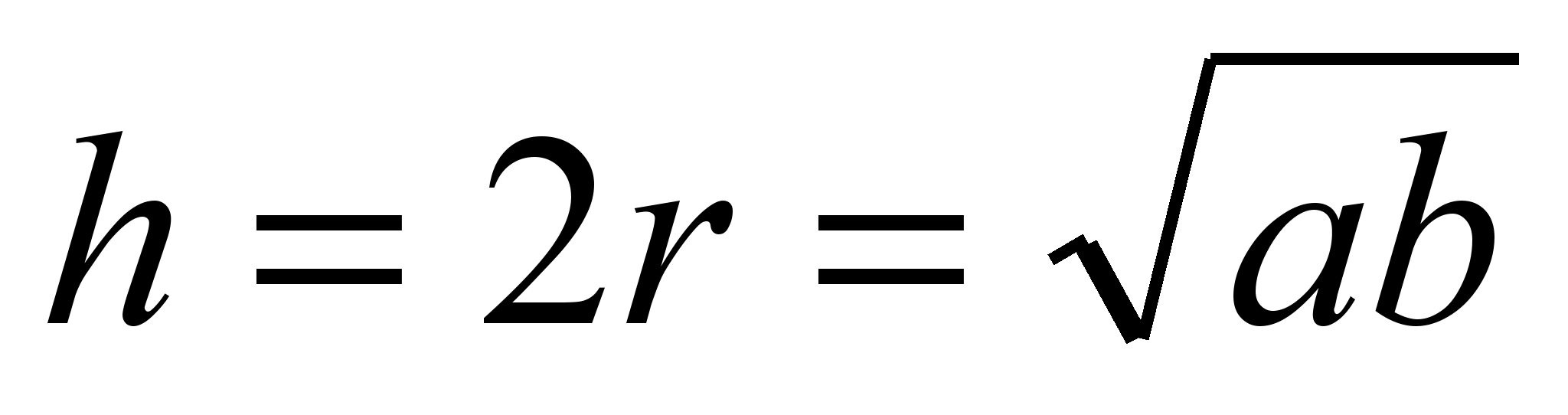 .
.