Bir üçgenin alanı nasıl bulunur? Bir üçgenin alanının ne olduğunu kanıtlayın
Üçgen herkesin aşina olduğu bir figür. Ve bu, formlarının zengin çeşitliliğine rağmen. Dikdörtgen, eşkenar, dar, ikizkenar, geniş. Her biri bir şekilde farklıdır. Ancak herkes için bir üçgenin alanını bulmanız gerekir.
Kenar uzunluklarını veya yüksekliklerini kullanan tüm üçgenlerde ortak olan formüller
İçlerinde benimsenen tanımlar: taraflar - a, b, c; a, n, n ile ilgili tarafların yükseklikleri.
1. Bir üçgenin alanı, ½'nin, bir kenarın ve yüksekliğin çarpımının bundan çıkarılmasıyla hesaplanır. S = ½ * a * n a. Diğer iki tarafın formülleri de benzer şekilde yazılmalıdır.
2. Yarı çevrenin göründüğü Heron formülü (tam çevrenin aksine genellikle küçük p harfiyle gösterilir). Yarı çevre şu şekilde hesaplanmalıdır: tüm kenarları toplayın ve 2'ye bölün. Yarı çevre formülü şu şekildedir: p = (a+b+c) / 2. O halde alanının eşitliği şekil şuna benzer: S = √ (p * (p - a) * ( р - в) * (р - с)).
3. Yarı çevre kullanmak istemiyorsanız, yalnızca kenar uzunluklarını içeren bir formül yararlı olacaktır: S = ¼ * √ ((a + b + c) * (b + c - a) ) * (a + c - c) * (a + b - c)). Bir öncekinden biraz daha uzun, ancak yarı çevreyi nasıl bulacağınızı unuttuysanız yardımcı olacaktır.
Bir üçgenin açılarını içeren genel formüller
Formülleri okumak için gereken gösterimler: α, β, γ - açılar. Sırasıyla a, b, c'nin karşılıklı taraflarında bulunurlar.
1. Buna göre iki tarafın çarpımının yarısı ile aralarındaki açının sinüsü üçgenin alanına eşittir. Yani: S = ½ a * b * sin γ. Diğer iki durumun formülleri de benzer şekilde yazılmalıdır.
2. Bir üçgenin alanı bir kenar ve üç kenar kullanılarak hesaplanabilir bilinen açılar. S = (a 2 * sin β * sin γ) / (2 sin α).
3. Ayrıca bilinen bir kenarı ve iki komşu açısı olan bir formül de vardır. Şuna benzer: S = c 2 / (2 (ctg α + ctg β)).
Son iki formül en basiti değil. Bunları hatırlamak oldukça zordur.
Yazılı veya çevrelenmiş dairelerin yarıçaplarının bilindiği durumlar için genel formüller
Ek tanımlar: r, R - yarıçap. Birincisi yazılı dairenin yarıçapı için kullanılır. İkincisi anlatılanlar içindir.
1. Bir üçgenin alanının hesaplandığı ilk formül yarı çevre ile ilgilidir. S = r * r. Bunu yazmanın başka bir yolu da şudur: S = ½ r * (a + b + c).
2. İkinci durumda, üçgenin tüm kenarlarını çarpmanız ve bunları çevrelenen dairenin yarıçapının dört katına bölmeniz gerekecektir. Gerçek ifadede şu şekilde görünür: S = (a * b * c) / (4R).
3. Üçüncü durum, kenarları bilmeden yapmanıza olanak sağlar ancak üç açının da değerlerine ihtiyacınız olacaktır. S = 2 R 2 * sin α * sin β * sin γ.
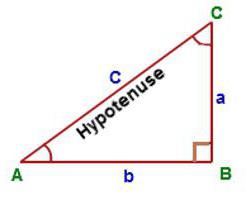
Özel durum: dik üçgen
Bu en basit durumdur çünkü yalnızca her iki bacağın uzunluğu da gereklidir. Latin harfleri a ve b ile gösterilirler. Bir dik üçgenin alanı, kendisine eklenen dikdörtgenin alanının yarısına eşittir.
Matematiksel olarak şuna benzer: S = ½ a * b. Hatırlanması en kolay olanıdır. Dikdörtgenin alan formülüne benzediğinden yalnızca yarımı gösteren bir kesir görünür.
Özel durum: ikizkenar üçgen
İki eşit kenara sahip olduğundan, alanıyla ilgili bazı formüller biraz basitleştirilmiş görünüyor. Örneğin, ikizkenar üçgenin alanını hesaplayan Heron formülü aşağıdaki formu alır:
S = ½ inç √((a + ½ inç)*(a - ½ inç)).
Eğer onu dönüştürürsen, kısalır. Bu durumda Heron'un ikizkenar üçgen formülü şu şekilde yazılır:
S = ¼ in √(4 * a 2 - b 2).
Alan formülü, eğer biliyorsanız, rastgele bir üçgenden biraz daha basit görünür. taraflar ve aralarındaki açı. S = ½ a 2 * sin β.
Özel durum: eşkenar üçgen
Genellikle problemlerde işin tarafı bilinir veya bir şekilde ortaya çıkarılabilir. Daha sonra böyle bir üçgenin alanını bulma formülü aşağıdaki gibidir:
S = (a 2 √3) / 4.
Üçgen kareli kağıt üzerinde gösteriliyorsa alanı bulma sorunları
En basit durum, bacakları kağıdın çizgileriyle çakışacak şekilde bir dik üçgenin çizilmesidir. O zaman bacaklara sığan hücre sayısını saymanız yeterlidir. Daha sonra bunları çarpın ve ikiye bölün.
Üçgen dar veya geniş olduğunda dikdörtgene çizilmesi gerekir. Daha sonra ortaya çıkan şekilde 3 üçgen olacaktır. Bunlardan biri problemde verilendir. Diğer ikisi ise yardımcı ve dikdörtgendir. Son ikisinin alanlarının yukarıda açıklanan yöntem kullanılarak belirlenmesi gerekir. Daha sonra dikdörtgenin alanını hesaplayın ve yardımcı olanlar için hesaplananları çıkarın. Üçgenin alanı belirlenir.
Üçgenin kenarlarının hiçbirinin kağıdın çizgileriyle çakışmaması durumu çok daha karmaşık hale geliyor. Daha sonra, orijinal şeklin köşelerinin yanlarında olması için bir dikdörtgenin içine yazılması gerekir. Bu durumda üç yardımcı dik üçgen olacaktır.
Heron formülünü kullanan bir problem örneği
Durum. Bazı üçgenlerin bilinen kenarları vardır. 3, 5 ve 6 cm'ye eşittirler, alanını bulmanız gerekiyor.
Artık yukarıdaki formülü kullanarak üçgenin alanını hesaplayabilirsiniz. Karekökün altında dört sayının çarpımı bulunur: 7, 4, 2 ve 1. Yani alan √(4 * 14) = 2 √(14)'tür.
Daha fazla doğruluk gerekmiyorsa 14'ün karekökünü alabilirsiniz. Bu 3,74'e eşittir. O zaman alan 7.48 olacaktır.
Cevap. S = 2 √14 cm2 veya 7,48 cm2.
Dik üçgenle ilgili örnek problem
Durum. Dik üçgenin bir bacağı ikincisinden 31 cm daha büyüktür, üçgenin alanı 180 cm2 ise uzunluklarını bulmanız gerekir.
Çözüm. İki denklemli bir sistemi çözmemiz gerekecek. Birincisi alanla ilgilidir. İkincisi problemde verilen bacakların oranıdır.
180 = ½ a * b;
a = b + 31.
Öncelikle ilk denklemde “a” değeri yerine yazılmalıdır. Görünüşe göre: 180 = ½ (+ 31) * inç. Tek bir bilinmeyen miktarı olduğundan çözülmesi kolaydır. Parantezleri açtıktan sonra ikinci dereceden denklem elde edilir: 2 + 31 360 = 0. Bu, "in" için iki değer verir: 9 ve - 40. İkinci sayı, kenar uzunluğu nedeniyle cevap olarak uygun değildir. Bir üçgenin değeri negatif olamaz.
Geriye ikinci ayağı hesaplamak kalıyor: Ortaya çıkan sayıya 31 ekleyin, 40 çıkıyor. Bunlar problemde aranan miktarlardır.
Cevap. Üçgenin bacakları 9 ve 40 cm'dir.
Bir üçgenin alanı, kenarı ve açısı boyunca bir kenar bulma problemi
Durum. Belirli bir üçgenin alanı 60 cm2'dir. İkinci kenar 15 cm ve aralarındaki açı 30° ise bir kenarını hesaplamak gerekir.
Çözüm. Kabul edilen gösterime göre istenilen kenar “a”, bilinen kenar “b”, verilen açı “γ”dır. Daha sonra alan formülü şu şekilde yeniden yazılabilir:
60 = ½ a * 15 * sin 30°. Burada 30 derecenin sinüsü 0,5'tir.
Dönüşümlerden sonra “a” 60 / (0,5 * 0,5 * 15) değerine eşit olur. Yani 16.
Cevap. Gerekli kenar 16 cm'dir.
Dik üçgenin içine yazılan kareyle ilgili problem
Durum. Bir kenarı 24 cm olan karenin tepe noktası üçgenin dik açısına denk gelir. Diğer ikisi yanlarda yatıyor. Üçüncüsü hipotenüse aittir. Bacaklardan birinin uzunluğu 42 cm'dir Dik üçgenin alanı nedir?
Çözüm. İki dik üçgen düşünün. Bunlardan ilki görevde belirtilendir. İkincisi orijinal üçgenin bilinen ayağına dayanmaktadır. Benzerdirler çünkü ortak açıları vardır ve paralel çizgilerden oluşurlar.
O halde bacaklarının oranları eşittir. Küçük üçgenin kenarları 24 cm'ye (karenin kenarı) ve 18 cm'ye eşittir (42 cm'lik kenardan karenin kenarını 24 cm çıkarırız). Büyük bir üçgenin karşılık gelen bacakları 42 cm ve x cm'dir, üçgenin alanını hesaplamak için gerekli olan bu “x”tir.
18/42 = 24/x yani x = 24*42/18 = 56 (cm) olur.
Daha sonra alan 56 ile 42'nin ikiye bölünmesine, yani 1176 cm2'ye eşittir.
Cevap. Gerekli alan 1176 cm2'dir.
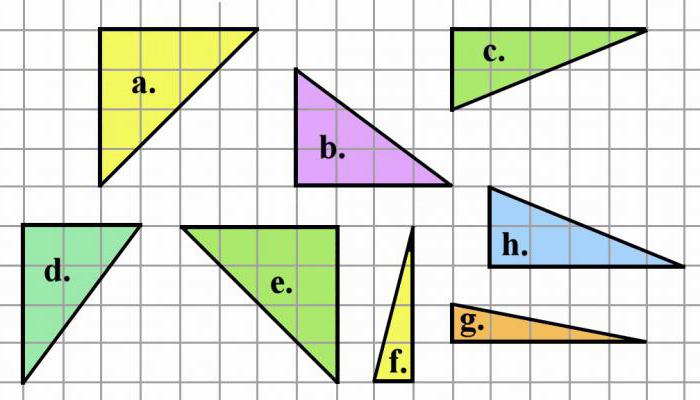
Bir üçgenin alanı, kenarının ve o kenardaki yüksekliğin çarpımının yarısına eşittir. Bu durumda yüksekliğin çizildiği tarafa genellikle taban denir. Böylece şunu söyleyebiliriz ki Bir üçgenin alanı taban ve yüksekliğinin çarpımının yarısına eşittir.
Üçgenin taban tarafının uzunluğunu a, yüksekliğini h olarak belirtirsek üçgenin alanı formülünü elde ederiz:
Bu formülü kanıtlamak için, yüksekliğin üçgendeki konumuna ilişkin tüm seçenekleri göz önünde bulundurmalısınız. Sadece üç tane var. Bu:
- Yükseklik üçgenin kenarlarından birine denk gelir. Bu durumda bacaklardan birinin taban olarak alındığı bir dik üçgenle karşı karşıyayız. Bu tarafa çizilen yükseklik diğer taraftır.
- Yükseklik üçgenin içindedir. Bu durumda tabanla kesişir ve onu iki parçaya böler. Bu durumda bu üçgen iki dik üçgene bölünür.
- Yükseklik üçgenin ötesine uzanır. Bu durumda tabanın kendisi ile değil, devamı ile (tabanın bulunduğu düz çizgi) kesişir.
İlk durumu ele alalım. ABC üçgeni verilsin. İçinde, BC kenarına denk gelen, a uzunluğundaki AC tabanına bir h yüksekliği çizilir:
Bildiğiniz gibi bir dikdörtgenin alanı bitişik kenarlarının çarpımına eşittir. Kenar uzunlukları a ve h olan bir dikdörtgenimiz olsaydı alanı ah'ye eşit olurdu. Bir dikdörtgenin içine bir köşegen çizerseniz, bu onu iki eşit dik açılı üçgene böler (üç kenarı da karşılık gelen şekilde eşittir). Bu üçgenlerin alanları da birbirine eşittir ve her biri dikdörtgenin tamamının alanının ½'sidir. Böylece bir üçgenin alanının olduğu kanıtlanmıştır. bu durumda½ ah'a eşit olacaktır.
İkinci durumu ele alalım. h uzunluğundaki BH yüksekliğinin a uzunluğundaki AC kenarıyla kesişmesine izin verin. 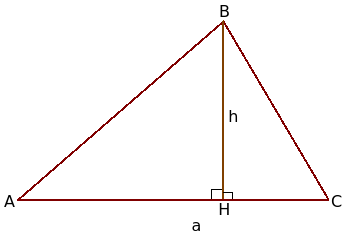
Bu durumda iki dik üçgen elde ederiz: ABH ve CBH. Ele alınan ilk durumdan, alanlarının sırasıyla ½ · AH · h ve ½ · CH · h'ye eşit olduğunu biliyoruz.
ABC üçgeninin tamamının alanı bu iki alanın toplamıdır:
S = ½ AH h + ½ CH h
Ortak faktörleri parantezlerden çıkaralım:
S = ½ saat (AH + CH)
Ancak AH ve CH'nin toplamı a uzunluğuna eşittir. Böylece kanıtlanması gereken formüle ulaşıyoruz:
S = ½ sa
Şimdi yüksekliğin üçgenin dışında olduğu üçüncü durumu düşünün: 
Burada ayrıca iki dik üçgen de görebiliriz. Bunlar ∆ABH ve ∆CBH'dir. Üstelik birincisi ikinciyi de içeriyor. İstenilen ABC üçgeni CBH üçgeninin ABH üçgenine tümleyenidir. Böylece ∆ABH alanının ∆CBH ve ∆ABC alanlarının toplamına eşit olduğunu yazabiliriz:
S ∆ABH = S ∆CBH + S ∆ABC
Gerekli ABC üçgeninin alanını nasıl buluruz:
S ∆ABC = S ∆ABH – S ∆CBH
ABH üçgeninin alanı ½ AH h, CBH üçgeninin alanı ½ CH h:
S ∆ABC = ½ AH h – ½ CH h
Ortak faktörleri parantezlerden çıkaralım:
S ∆ABC = ½ sa (AH – CH)
Ancak CH parçasını AH kısmından çıkarırsanız uzunluğu a'ya eşit olan bir AC parçası elde edersiniz. Dolayısıyla bu durumda üçgenin alanının da ½ ah olduğunu yazabiliriz.
Bir üçgenin alanını belirlemek için farklı formüller kullanabilirsiniz. Tüm yöntemler arasında en kolay ve en sık kullanılanı, yüksekliği taban uzunluğuyla çarpmak ve ardından sonucu ikiye bölmektir. Ancak bu yöntem tek yöntem olmaktan uzaktır. Aşağıda farklı formüller kullanarak bir üçgenin alanının nasıl bulunacağını okuyabilirsiniz.
Ayrı olarak, belirli üçgen türlerinin (dikdörtgen, ikizkenar ve eşkenar) alanını hesaplamanın yollarına bakacağız. Her formüle, özünü anlamanıza yardımcı olacak kısa bir açıklama ekliyoruz.
Bir üçgenin alanını bulmak için evrensel yöntemler
Aşağıdaki formüller özel gösterim kullanır. Her birinin şifresini çözeceğiz:
- a, b, c – ele aldığımız şeklin üç tarafının uzunlukları;
- r, üçgenimize yazılabilecek dairenin yarıçapıdır;
- R, çevresinde tanımlanabilecek dairenin yarıçapıdır;
- α, b ve c kenarlarının oluşturduğu açının büyüklüğüdür;
- β a ve c arasındaki açının büyüklüğüdür;
- γ, a ve b taraflarının oluşturduğu açının büyüklüğüdür;
- h, üçgenimizin α açısından a kenarına indirilmiş yüksekliğidir;
- p – a, b ve c kenarlarının toplamının yarısı.
Bir üçgenin alanını neden bu şekilde bulabileceğiniz mantıksal olarak açıktır. Üçgen, üçgenin bir tarafının köşegen görevi göreceği bir paralelkenar halinde kolayca tamamlanabilir. Paralelkenarın alanı, kenarlarından birinin uzunluğunun kendisine çizilen yüksekliğin değeriyle çarpılmasıyla bulunur. Köşegen bu koşullu paralelkenarı 2 özdeş üçgene böler. Dolayısıyla orijinal üçgenimizin alanının bu yardımcı paralelkenarın alanının yarısına eşit olması gerektiği oldukça açıktır.
S=½ a b sin γ
Bu formüle göre bir üçgenin alanı, iki kenarının (a ve b) uzunluklarının, bunların oluşturduğu açının sinüsüyle çarpılmasıyla bulunur. Bu formül mantıksal olarak öncekinden türetilmiştir. Yüksekliği β açısından b kenarına indirirsek, dik üçgenin özelliklerine göre a tarafının uzunluğunu γ açısının sinüsüyle çarptığımızda üçgenin yüksekliğini yani h'yi elde ederiz. .
Söz konusu şeklin alanı, içine yazılabilecek dairenin yarıçapının yarısının çevresi ile çarpılmasıyla bulunur. Yani söz konusu dairenin yarı çevresi ile yarıçapının çarpımını buluyoruz.
S= a b c/4R
Bu formüle göre ihtiyacımız olan değer, şeklin kenarlarının çarpımının, çevresinde tanımlanan dairenin 4 yarıçapına bölünmesiyle bulunabilir.
Bu formüller evrenseldir, çünkü herhangi bir üçgenin (çeşitkenar, ikizkenar, eşkenar, dikdörtgen) alanını belirlemeyi mümkün kılarlar. Bu, üzerinde ayrıntılı olarak durmayacağımız daha karmaşık hesaplamalar kullanılarak yapılabilir.
Belirli özelliklere sahip üçgenlerin alanları
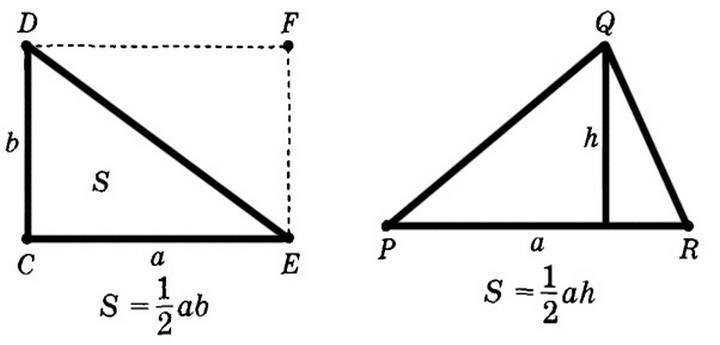
Dik üçgenin alanı nasıl bulunur? Bu şeklin özelliği, iki tarafının aynı anda yüksekliği olmasıdır. Eğer a ve b kenarlar ise ve c hipotenüs olursa, alanı şu şekilde buluruz:
İkizkenar üçgenin alanı nasıl bulunur? A uzunluğunda iki kenarı ve b uzunluğunda bir kenarı vardır. Sonuç olarak alanı, a tarafının karesinin çarpımının γ açısının sinüsüne 2'ye bölünmesiyle belirlenebilir.
Alan nasıl bulunur? eşkenar üçgen? İçinde tüm kenarların uzunluğu a'ya eşittir ve tüm açıların büyüklüğü α'dır. Yüksekliği, a tarafının uzunluğunun ve 3'ün karekökünün çarpımının yarısına eşittir. Normal bir üçgenin alanını bulmak için, a tarafının karesini 3'ün kareköküyle çarpmanız ve şuna bölmeniz gerekir: 4.
Bir üçgenin alanı. Birleşik Devlet Sınavı görevleri de dahil olmak üzere alanların hesaplanmasıyla ilgili birçok geometri probleminde üçgenin alanı için formüller kullanılır. Bunlardan birkaçı var, burada ana olanlara bakacağız.
Bu formülleri listelemek çok basit olur; referans kitaplarında ve çeşitli web sitelerinde bu tür şeylerden zaten yeterince var. Bazılarının özünü aktarmak istiyorum. Makaledeki materyali inceledikten sonra tüm formülleri öğrenmenize gerek olmadığını, onları anlamanız gerektiğini anlayacaksınız.
Doğru anda aniden “uçup giderlerse” onları hafızanızda kolayca hatırlayabilirsiniz. Öncelikle paralelkenara bakalım. Tanım şöyle:
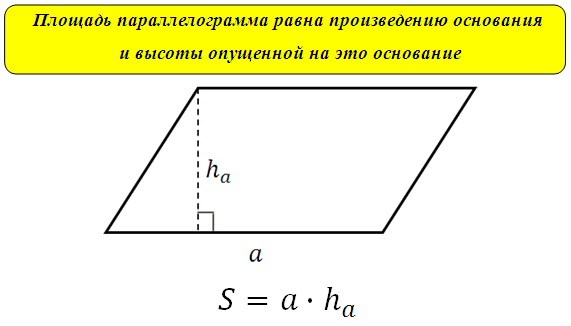
Nedenmiş? Basit! Formülün anlamının ne olduğunu açıkça göstermek için bazı ek yapılar yapalım:

Üçgenin (2) alanı, üçgenin (1) alanına eşittir, ikinciyi zihinsel olarak “keser” ve onu birincinin üzerine gelecek şekilde hareket ettirir, alanı eşit olan bir dikdörtgen elde ederiz. orijinal paralelkenarın alanı:

Bir dikdörtgenin alanının bitişik kenarlarının çarpımına eşit olduğu bilinmektedir. Çizimden görülebileceği gibi, ortaya çıkan dikdörtgenin bir tarafı paralelkenarın kenarına eşit, diğer tarafı ise bu tarafa çizilen yüksekliğidir. Bu nedenle, S = a∙h paralelkenarının alanı için formül elde ederiz. A
Alanı için başka bir formülle devam edelim. Sahibiz:
![]()
h a yüksekliğini ifade edelim dik üçgen burada b hipotenüstür:
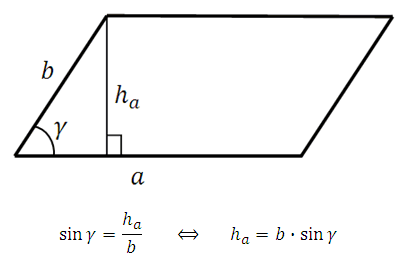
Alan formülünde h a'yı yerine koyarsak şunu elde ederiz:

Paralelkenarın çözümünü yaptık. Şimdi üçgene geçelim.
Bir üçgenin alanı. Altı formül!
İlk formül
Paralelkenarın köşegeni onu eşit alanlı iki üçgene böler:
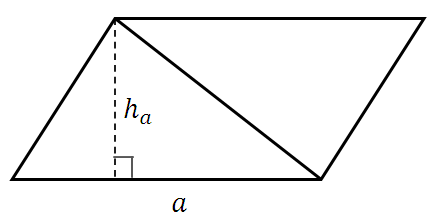
Bu nedenle üçgenin alanı paralelkenarın alanının yarısına eşit olacaktır:
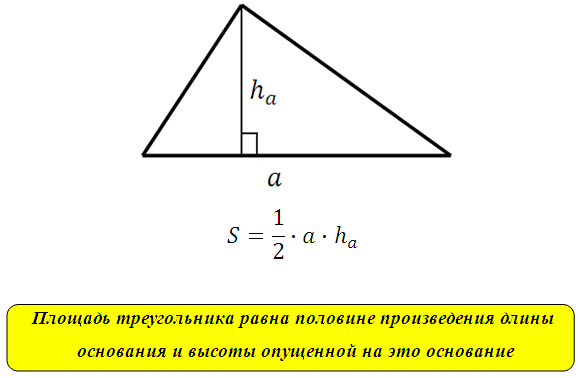
*Yani üçgenin herhangi bir kenarını ve bu kenara indirilen yüksekliği biliyorsak, bu üçgenin alanını her zaman hesaplayabiliriz.
Formül iki
Daha önce de söylediğimiz gibi paralelkenarın alanı formülü şöyledir:
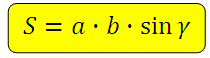
Bir üçgenin alanı, alanının yarısına eşittir, bu şu anlama gelir:
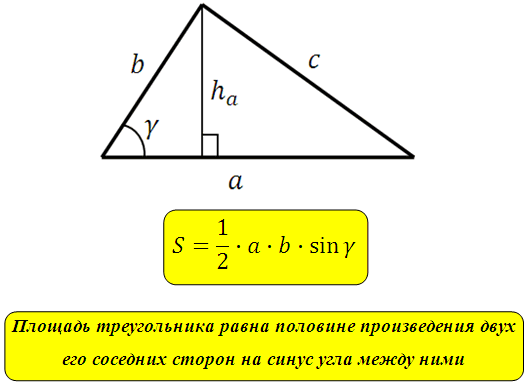
*Yani bir üçgenin herhangi iki kenarı ve aralarındaki açı biliniyorsa, böyle bir üçgenin alanını her zaman hesaplayabiliriz.
Heron formülü (üçüncü)
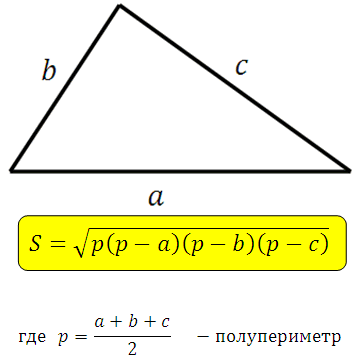
Bu formülün elde edilmesi zordur ve işinize yaramaz. Bakın ne kadar güzel, kendisinin unutulmaz olduğunu söyleyebilirsiniz.
*Bir üçgenin üç kenarı verilmişse bu formülü kullanarak üçgenin alanını her zaman hesaplayabiliriz.
Formül dört
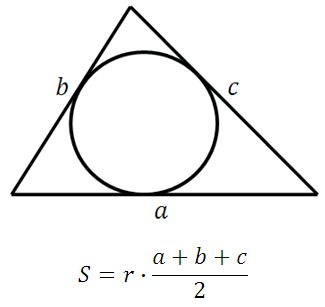
Nerede R– yazılı dairenin yarıçapı
*Bir üçgenin üç kenarı ve içine yazılan dairenin yarıçapı biliniyorsa bu üçgenin alanını her zaman bulabiliriz.
Formül beş
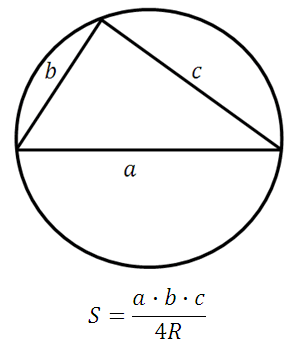
Nerede R– çevrelenmiş dairenin yarıçapı.
*Bir üçgenin üç kenarı ve onu çevreleyen dairenin yarıçapı biliniyorsa, böyle bir üçgenin alanını her zaman bulabiliriz.
Şu soru ortaya çıkıyor: Bir üçgenin üç tarafı biliniyorsa, Heron formülünü kullanarak alanını bulmak daha kolay değil mi?
Evet, daha kolay olabilir ama her zaman değil, bazen karmaşıklık ortaya çıkabilir. Bu, kökün çıkarılmasını içerir. Ayrıca bu formüller, bir üçgenin alanının ve kenarlarının verildiği ve yazılı veya çevrelenmiş dairenin yarıçapını bulmanız gereken problemlerde kullanıma çok uygundur. Bu tür görevler Birleşik Devlet Sınavının bir parçası olarak mevcuttur.
Okumak faydalı olabilir:
- 100'de haşlanmış pirinç karbonhidratı;
- Kıyılmış tavuklu tembel lahana ruloları;
- Çedar peynirinin kalori içeriği ve kontrendikasyonları;
- Tavuk göğsünde kaç kalori var;
- Fesleğen yemek pişirmede nasıl kullanılır, hangi yemeklere eklenir ve hangi baharatlarla karıştırılır?;
- Keten tohumu unundan brownie nasıl yapılır: sağlıklı ve çok lezzetli!;
- Kepek - sağlık için kullanıma yönelik türleri, faydalı özellikleri ve tarifleri Kepek ne içerir?;
- Sansasyonel bir ürün kullanmanın incelikleri;