cos nisbati. To'g'ri uchburchak. Misollar bilan batafsil nazariya
Ko'rsatma
Usul 1. Pifagor teoremasidan foydalanish. Teorema shunday deydi: gipotenuzaning kvadrati oyoqlarning kvadratlari yig'indisiga teng. Bundan kelib chiqadiki, to'g'ri burchakli uchburchakning istalgan tomonini uning boshqa ikki tomonini bilgan holda hisoblash mumkin (2-rasm).
2-usul. Bundan kelib chiqadiki, mediana chizilgan to'g'ri burchak gipotenuzaga oʻzaro 3 ta oʻxshash uchburchak hosil qiladi (3-rasm). Bu rasmda ABC, BCD va ACD uchburchaklari o'xshash.
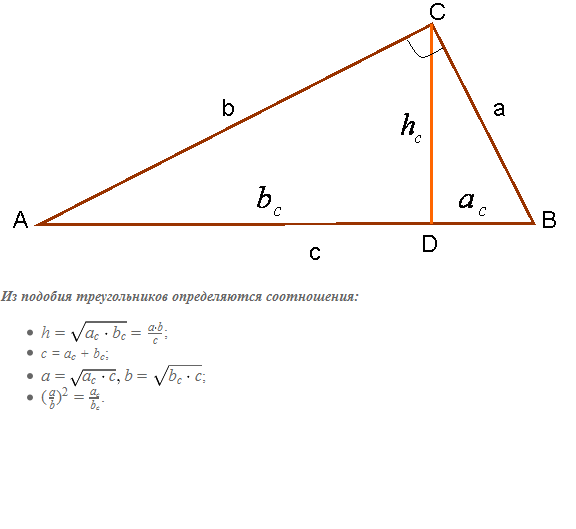
Gipotenuza - to'g'ri burchakli uchburchakning 90 graduslik burchakka qarama-qarshi tomoni. Uning uzunligini hisoblash uchun oyoqlardan birining uzunligini va uchburchakning o'tkir burchaklaridan birining qiymatini bilish kifoya.

Ko'rsatma
Ma'lum oyog'i va to'g'ri burchakli uchburchakning o'tkir burchagi bilan, gipotenuzaning o'lchami oyoqning ushbu burchakning kosinusiga / sinusiga nisbatiga teng bo'lishi mumkin, agar bu burchak unga qarama-qarshi / qo'shni bo'lsa:
h = C1(yoki C2)/sina;
h = S1(yoki S2)/cosa.
Misol: AB gipotenuzasi va to‘g‘ri burchagi C bo‘lgan ABC to‘g‘ri burchakli uchburchak berilgan.B burchak 60 gradus va A burchak 30 gradus bo‘lsin.BC oyog‘ining uzunligi 8 sm.AB gipotenuzasi uzunligini toping. Buning uchun siz yuqorida tavsiya etilgan usullardan birini qo'llashingiz mumkin:
AB=BC/cos60=8 sm.
AB = BC/sin30 = 8 sm.
Gipotenuza - to'g'ri burchakka qarama-qarshi bo'lgan to'g'ri burchakli uchburchakning tomoni. Bu to'g'ri burchakli uchburchakning eng uzun tomoni. Siz uni Pifagor teoremasi yoki trigonometrik funktsiyalar formulalari yordamida hisoblashingiz mumkin.
![]()
Ko'rsatma
Oyoqlar to'g'ri burchakka ulashgan to'g'ri burchakli uchburchakning tomonlari deb ataladi. Rasmda oyoqlar AB va BC sifatida belgilangan. Ikkala oyoqning uzunligi ham berilsin. Ularni |AB| deb belgilaymiz va |BC|. Gipotenuzaning uzunligini |AC| topish uchun Pifagor teoremasidan foydalanamiz. Ushbu teoremaga ko'ra, oyoqlarning kvadratlari yig'indisi gipotenuzaning kvadratiga teng, ya'ni. chizmamiz yozuvida |AB|^2 + |BC|^2 = |AC|^2. Formuladan AC gipotenuzasi uzunligi |AC| shaklida topilganligini olamiz = √(|AB|^2 + |BC|^2) .
Bir misolni ko'rib chiqing. Oyoqlarning uzunliklari |AB| bo'lsin = 13, |BC| = 21. Pifagor teoremasi bo'yicha biz |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610 ni olamiz. 610 raqamidan: |AC| = √610. Butun sonlar kvadratlari jadvalidan foydalanib, 610 soni hech qanday butun sonning mukammal kvadrati emasligini aniqlaymiz. Gipotenuza uzunligining yakuniy qiymatini olish uchun ildiz belgisi ostidan to'liq kvadratni olishga harakat qilaylik. Buning uchun biz 610 raqamini omillarga ajratamiz. 610 = 2 * 5 * 61. Jadvalga ko'ra tub sonlar Biz 61 ning tub son ekanligini ko'ramiz. Shuning uchun √610 raqamini yanada qisqartirish mumkin emas. Biz yakuniy javobni |AC| olamiz = √610.
Agar gipotenuzaning kvadrati, masalan, 675 bo'lsa, u holda √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. Agar bunday quyish mumkin bo'lsa, teskari tekshiruvni bajaring - natijani kvadratga aylantiring va asl qiymat bilan solishtiring.
Bizga oyoqlardan birini va unga ulashgan burchakni bilib olaylik. Aniqlik uchun u |AB| oyog'i bo'lsin va burchak a. Keyin trigonometrik funktsiya kosinus uchun formuladan foydalanishimiz mumkin - burchakning kosinasi qo'shni oyoqning gipotenuzaga nisbatiga teng. Bular. yozuvimizda cos a = |AB| / |AC|. Bu yerdan gipotenuzaning uzunligini |AC| olamiz = |AB| / cosa.
Agar oyog'ini bilsak |BC| va burchak a, keyin burchak sinusini hisoblash uchun formuladan foydalanamiz - burchak sinusi qarama-qarshi oyoqning gipotenuzaga nisbatiga teng: sin a = |BC| / |AC|. Gipotenuzaning uzunligi |AC| shaklida topilganligini olamiz = |BC| / cosa.
Aniqlik uchun misolni ko'rib chiqing. Oyoqning uzunligi |AB| bo'lsin = 15. Va burchak a = 60 °. Biz |AC|ni olamiz = 15 / cos 60 ° = 15 / 0,5 = 30.
Natijangizni Pifagor teoremasi yordamida qanday tekshirish mumkinligini ko'rib chiqing. Buning uchun |BC| ikkinchi oyog'ining uzunligini hisoblashimiz kerak. tg a = |BC| burchak tangensi formulasidan foydalanib / |AC|, biz |BC| olamiz = |AB| * tg a = 15 * tg 60° = 15 * √3. Keyinchalik, biz Pifagor teoremasini qo'llaymiz, biz 15^2 + (15 * √3)^2 = 30^2 => 225 + 675 = 900 ni olamiz. Tekshiruv amalga oshirildi.
Gipotenuzani hisoblagandan so'ng, olingan qiymat Pifagor teoremasiga mos keladimi yoki yo'qligini tekshiring.
Manbalar:
- 1 dan 10000 gacha tub sonlar jadvali
Oyoqlar to'g'ri burchakli uchburchakning uchini tashkil etuvchi ikkita qisqa tomonini nomlang, ularning qiymati 90 °. Bunday uchburchakdagi uchinchi tomon gipotenuza deyiladi. Uchburchakning barcha tomonlari va burchaklari, agar bir nechta boshqa parametrlar ma'lum bo'lsa, oyoq uzunligini hisoblash imkonini beruvchi ma'lum munosabatlar bilan bir-biriga bog'langan.

Ko'rsatma
To'g'ri burchakli uchburchakning qolgan ikki tomonining (B va C) uzunligini bilsangiz, oyoq uzunligini (A) hisoblash uchun Pifagor teoremasidan foydalaning. Bu teoremada aytilishicha, oyoqlarning kvadrati uzunliklarining yig'indisi gipotenuzaning kvadratiga teng. Bundan kelib chiqadiki, har bir oyoqning uzunligi gipotenuza va ikkinchi oyoq uzunliklari kvadratlari ayirmasining kvadrat ildiziga teng: A=√(C²-B²).
Hisoblangan oyoqqa qarama-qarshi burchakning (a) qiymatini va gipotenuzaning uzunligini (C) bilsangiz, o'tkir burchak uchun to'g'ridan-to'g'ri trigonometrik funktsiyaning "sinus" ta'rifidan foydalaning. Bu ta'rif buning sinusi ekanligini bildiradi ma'lum burchak kerakli oyoq uzunligining gipotenuzaning uzunligiga nisbatiga teng. Bu shuni anglatadiki, kerakli oyoq uzunligi gipotenuzaning uzunligi va ma'lum burchak sinusining ko'paytmasiga teng: A=C∗sin(a). Xuddi shu ma'lum qiymatlar uchun siz kosekant funktsiyasining ta'rifidan foydalanishingiz va gipotenuzaning uzunligini A=C/kosek(a) ma'lum burchakning kosekantiga bo'lish orqali kerakli uzunlikni hisoblashingiz mumkin.
To'g'ridan-to'g'ri trigonometrik funktsiya kosinusning ta'rifidan foydalaning, agar gipotenuzaning uzunligi (C) dan tashqari, kerakli oyoqqa qo'shni o'tkir burchakning (b) qiymati ham ma'lum bo'lsa. Bu burchakning kosinusu kerakli oyoq va gipotenuzaning uzunliklarining nisbati sifatida aniqlanadi va bundan xulosa qilishimiz mumkinki, oyoq uzunligi gipotenuzaning uzunligi va ma'lum bo'lgan kosinusning ko'paytmasiga teng. burchak: A=C∗cos(b). Siz sekant funksiyasining ta'rifidan foydalanishingiz va gipotenuzaning uzunligini ma'lum burchak A=C/sek(b) sekantiga bo'lish orqali kerakli qiymatni hisoblashingiz mumkin.
Trigonometrik funktsiya tangensining hosilasi uchun shunga o'xshash ta'rifdan kerakli formulani chiqaring, agar kerakli oyoq (A) qarshisida joylashgan o'tkir burchakning (a) qiymatiga qo'shimcha ravishda, ikkinchi oyoqning uzunligi (B) bo'lsa. ma'lum. Kerakli oyoqqa qarama-qarshi burchakning tangensi - bu oyoq uzunligining ikkinchi oyoq uzunligiga nisbati. Bu shuni anglatadiki, kerakli qiymat ma'lum oyoq uzunligi va ma'lum burchak tangensi ko'paytmasiga teng bo'ladi: A=B∗tg(a). Xuddi shu ma'lum miqdorlardan kotangent funksiyaning ta'rifi yordamida boshqa formulani olish mumkin. Bunday holda, oyoq uzunligini hisoblash uchun ma'lum bo'lgan oyoq uzunligining ma'lum burchak kotangentiga nisbatini topish kerak bo'ladi: A=B/ctg(a).
Tegishli videolar
"Katet" so'zi rus tiliga yunon tilidan kelgan. Aniq tarjimada bu plumb chizig'ini, ya'ni er yuzasiga perpendikulyar degan ma'noni anglatadi. Matematikada oyoqlar to'g'ri burchakli uchburchakning to'g'ri burchagini tashkil etuvchi tomonlar deb ataladi. Bu burchakka qarama-qarshi tomon gipotenuza deyiladi. "Oyoq" atamasi arxitektura va payvandlash texnologiyasida ham qo'llaniladi.

ACB to‘g‘ri burchakli uchburchakni chizing. Uning oyoqlarini a va b, gipotenuzasiga c belgi qo'ying. To'g'ri burchakli uchburchakning barcha tomonlari va burchaklari ma'lum munosabatlar bilan bog'langan. O'tkir burchaklardan biriga qarama-qarshi bo'lgan oyoqning gipotenuzaga nisbati bu burchakning sinusi deyiladi. Bu uchburchakda sinCAB=a/c. Kosinus - qo'shni oyoqning gipotenuzasiga nisbati, ya'ni cosCAB=b/c. Teskari aloqalar sekant va kosekant deb ataladi.
Bu burchakning sekanti gipotenuzani qo'shni oyoqqa bo'lish yo'li bilan olinadi, ya'ni secCAB=c/b. Kosinusning o'zaro ta'siri chiqadi, ya'ni uni secCAB=1/cosSAB formulasi bilan ifodalash mumkin.
Kosekant gipotenuzani qarama-qarshi oyoqqa bo'lish qismiga teng va sinusning o'zaro nisbati. Uni cosecCAB=1/sinCAB formulasi yordamida hisoblash mumkin
Ikkala oyoq ham tangens va kotangens orqali bog'langan. IN bu holat tangens a tomonining b tomoniga nisbati bo'ladi, ya'ni qarama-qarshi oyoq qo'shnisiga. Bu nisbatni tgCAB=a/b formulasi bilan ifodalash mumkin. Shunga ko'ra, teskari nisbat kotangent bo'ladi: ctgCAB=b/a.
Gipotenuzaning va ikkala oyoqning o'lchamlari o'rtasidagi nisbat qadimgi yunon matematigi Pifagor tomonidan aniqlangan. Uning nomi bilan atalgan teorema hali ham odamlar tomonidan qo'llaniladi. Unda aytilishicha, gipotenuzaning kvadrati oyoqlarning kvadratlari yig'indisiga teng, ya'ni c2 \u003d a2 + b2. Shunga ko'ra, har bir oyoq gipotenuza va boshqa oyoq kvadratlari orasidagi farqning kvadrat ildiziga teng bo'ladi. Bu formulani b=√(c2-a2) shaklida yozish mumkin.
Oyoqning uzunligi siz bilgan munosabatlar orqali ham ifodalanishi mumkin. Sinuslar va kosinuslar teoremalariga ko'ra, oyoq gipotenuza va ushbu funktsiyalardan birining mahsulotiga teng. U tangens yoki kotangens bilan ham ifodalanishi mumkin. A oyog'ini, masalan, a \u003d b * tan CAB formulasi bo'yicha topish mumkin. Aynan shu tarzda, berilgan tangens yoki kotangensga qarab, ikkinchi oyoq aniqlanadi.
Arxitekturada "oyoq" atamasi ham qo'llaniladi. U ion kapitaliga qo'llaniladi va uning orqa tomonining o'rtasidan o'tuvchi chiziqni bildiradi. Ya'ni, bu holda, bu atama berilgan chiziqqa perpendikulyarni bildiradi.
Payvandlash texnologiyasida "oyoq filesi payvandlash" tushunchasi mavjud. Boshqa hollarda bo'lgani kabi, bu eng qisqa masofa. Bu yerga gaplashamiz boshqa qismning yuzasida joylashgan tikuv chegarasiga payvandlanadigan qismlardan biri orasidagi bo'shliq haqida.
Tegishli videolar
Manbalar:
- oyoq va gipotenuza nima
Tegishli videolar
Eslatma
To'g'ri burchakli uchburchakning tomonlarini hisoblashda uning xususiyatlari to'g'risidagi bilimlar o'ynashi mumkin:
1) To'g'ri burchakning oyog'i 30 gradus burchakka qarama-qarshi yotsa, u gipotenuzaning yarmiga teng;
2) gipotenuza har qanday oyoqdan hamisha uzunroq;
3) Agar aylana to'g'ri burchakli uchburchak atrofida o'ralgan bo'lsa, uning markazi gipotenuzaning o'rtasida yotishi kerak.
Trigonometriya - trigonometrik funktsiyalarni, shuningdek, ulardan amaliyotda foydalanishni o'rganadigan matematikaning bo'limi. Bu xususiyatlar o'z ichiga oladi sinus, kosinus, tangens va kotangens.
Sinus trigonometrik funktsiya , qarama-qarshi oyoq kattaligining gipotenuzaning kattaligiga nisbati.
Trigonometriyada sinus.
Yuqorida aytib o'tilganidek, sinus trigonometriya va trigonometrik funktsiyalar bilan bevosita bog'liq. Uning funktsiyasi bilan belgilanadi
- uchburchak tomonlarining o'lchamlari ma'lum bo'lishi sharti bilan burchakni hisoblashda yordam berish;
- burchak ma'lum bo'lgan taqdirda, uchburchak tomonining o'lchamini hisoblashda yordam beradi.
Shuni esda tutish kerakki, sinusning qiymati har doim uchburchakning har qanday o'lchami uchun bir xil bo'ladi, chunki sinus o'lchov emas, balki nisbatdir.
Binobarin, ma'lum bir muammoning har bir yechimi uchun bu doimiy qiymatni hisoblamaslik uchun maxsus trigonometrik jadvallar yaratilgan. Ularda sinuslar, kosinuslar, tangenslar va kotangenslarning qiymatlari allaqachon hisoblangan va aniqlangan. Odatda, bu jadvallar algebra va geometriya darsliklarining varaqlarida keltirilgan. Ularni Internetda ham topish mumkin.
Geometriyada sinus.
Geometriya vizualizatsiyani talab qiladi, shuning uchun amalda tushunish uchun burchakning sinusi nimaga teng, to'g'ri burchakli uchburchak chizishingiz kerak.
Faraz qilaylik, to'g'ri burchak hosil qiluvchi tomonlar nomlanadi a, c, qarama-qarshi burchak X.
Odatda tomonlarning uzunligi vazifalarda ko'rsatiladi. Aytaylik a=3, b=4. Bunday holda, tomonlar nisbati ¾ kabi ko'rinadi. Bundan tashqari, agar biz uchburchakning o'tkir burchakka ulashgan tomonlarini uzaytirsak X, keyin tomonlar ortadi A Va V, va gipotenuza - to'g'ri burchakli uchburchakning asosiga to'g'ri burchak ostida bo'lmagan uchinchi tomoni. Endi uchburchakning tomonlarini boshqacha chaqirish mumkin, masalan: m, n, k.
Ushbu modifikatsiya bilan trigonometriya qonuni ishladi: uchburchak tomonlarining uzunligi o'zgardi, lekin ularning nisbati o'zgarmadi.
Qadimgi olimlar uchburchakning tomonlari uzunligini xohlagancha o'zgartirsangiz va x burchak qiymatini saqlab tursangiz, uning tomonlari orasidagi nisbat o'zgarishsiz qolishi haqiqatini payqashgan. Bizning holatda, tomonlarning uzunligi quyidagicha o'zgarishi mumkin: a / b \u003d ¾, yon tomoni uzaytirilganda A 6 sm gacha, va V- 8 sm gacha biz olamiz: m/n = 6/8 = 3/4.
To'g'ri burchakli uchburchakda tomonlarning nisbati deyiladi:
- x burchakning sinusi qarama-qarshi oyoqning gipotenuzaga nisbati: sinx = a/c;
- x burchakning kosinusu - qo'shni oyoqning gipotenuzaga nisbati: cosx = w/s;
- x burchakning tangensi - qarama-qarshi oyoqning qo'shnisiga nisbati: tgx \u003d a / b;
- x burchakning kotangenti - qo'shni oyoqning qarama-qarshisiga nisbati: ctgx \u003d in / a.
Biz trigonometriyani o'rganishni to'g'ri burchakli uchburchakdan boshlaymiz. Keling, sinus va kosinus nima ekanligini, shuningdek, o'tkir burchakning tangensi va kotangensini aniqlaymiz. Bu trigonometriyaning asoslari.
Shuni eslang to'g'ri burchak ga teng burchak hisoblanadi. Boshqacha qilib aytganda, ochilgan burchakning yarmi.
O'tkir burchak- kichikroq.
O'tkir burchak- kattaroq. Bunday burchakka nisbatan "to'mtoq" haqorat emas, balki matematik atama :-)

Keling, to'g'ri burchakli uchburchak chizamiz. To'g'ri burchak odatda belgilanadi. E'tibor bering, burchakka qarama-qarshi tomon bir xil harf bilan belgilanadi, faqat kichik. Demak, burchakka qarama-qarshi yotgan tomon belgilanadi.
Burchak tegishli yunoncha harf bilan belgilanadi.
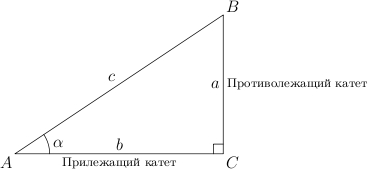
Gipotenuza To'g'ri uchburchak - bu to'g'ri burchakka qarama-qarshi tomon.
Oyoqlar- o'tkir burchaklarga qarama-qarshi tomonlar.
Burchakning qarshisidagi oyoq deyiladi qarama-qarshi(burchakka nisbatan). Burchakning bir tomonida yotgan boshqa oyog'i deyiladi qo'shni.
Sinus To'g'ri burchakli uchburchakdagi o'tkir burchak - bu qarama-qarshi oyoqning gipotenuzaga nisbati:
Kosinus To'g'ri uchburchakdagi o'tkir burchak - qo'shni oyoqning gipotenuzaga nisbati:
Tangent To'g'ri uchburchakdagi o'tkir burchak - qarama-qarshi oyoqning qo'shniga nisbati:
Boshqa (ekvivalent) ta'rif: o'tkir burchakning tangensi - bu burchak sinusining uning kosinusiga nisbati:
![]()
Kotangent To'g'ri uchburchakdagi o'tkir burchak - qo'shni oyoqning teskarisiga nisbati (yoki ekvivalenti kosinusning sinusga nisbati):
![]()
Quyida keltirilgan sinus, kosinus, tangens va kotangensning asosiy nisbatlariga e'tibor bering. Ular bizga muammolarni hal qilishda foydali bo'ladi.
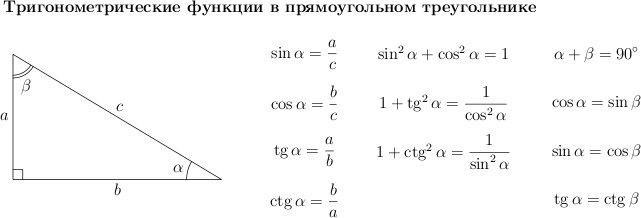
Keling, ulardan ba'zilarini isbotlaylik.
1. Har qanday uchburchak burchaklarining yig'indisi ga teng. Ma'nosi, to'g'ri burchakli uchburchakning ikkita o'tkir burchagi yig'indisi .
2. Bir tomondan, qarama-qarshi oyoqning gipotenuzaga nisbati sifatida. Boshqa tomondan, chunki burchak uchun oyoq qo'shni bo'ladi.
Biz buni tushunamiz ![]() . Boshqa so'zlar bilan aytganda, .
. Boshqa so'zlar bilan aytganda, .
3. Pifagor teoremasini oling: ![]() . Keling, ikkala qismni quyidagilarga ajratamiz:
. Keling, ikkala qismni quyidagilarga ajratamiz:
![]()
Bizda bor asosiy trigonometrik identifikatsiya:
Shunday qilib, burchakning sinusini bilib, uning kosinusini topishimiz mumkin va aksincha.
4. Asosiy trigonometrik identifikatsiyaning ikkala qismini ga bo‘lib, quyidagilarga erishamiz:
![]()
Bu shuni anglatadiki, agar bizga o'tkir burchakning tangensi berilsa, biz darhol uning kosinusini topishimiz mumkin.
Xuddi shunday,
![]()
Yaxshi, biz ta'riflar va yozma formulalar berdik. Lekin nima uchun bizga sinus, kosinus, tangens va kotangens kerak?
Biz buni bilamiz har qanday uchburchakning burchaklarining yig'indisi.
o'rtasidagi munosabatni bilamiz partiyalar to'g'ri uchburchak. Bu Pifagor teoremasi: ![]() .
.
Ma'lum bo'lishicha, uchburchakdagi ikkita burchakni bilib, uchinchisini topishingiz mumkin. To'g'ri uchburchakda ikki tomonni bilib, uchinchisini topishingiz mumkin. Shunday qilib, burchaklar uchun - ularning nisbati, tomonlar uchun - o'z. Ammo to'g'ri burchakli uchburchakda bitta burchak (to'g'ri burchakdan tashqari) va bir tomoni ma'lum bo'lsa, nima qilish kerak, lekin siz boshqa tomonlarni topishingiz kerak?
Dastlab, sinus va kosinus to'g'ri burchakli uchburchaklardagi miqdorlarni hisoblash zarurati tufayli paydo bo'lgan. Agar to'g'ri burchakli uchburchakdagi burchaklarning daraja o'lchovining qiymati o'zgarmasa, tomonlarning nisbati, bu tomonlar uzunligi qanchalik o'zgarmasin, har doim bir xil bo'lib qolishi ta'kidlandi.Shunday qilib sinus va kosinus tushunchalari kiritildi. To'g'ri burchakli uchburchakdagi o'tkir burchakning sinusi qarama-qarshi oyoqning gipotenuzaga nisbati, kosinus esa qo'shni oyoqning gipotenuzaga nisbati.
Kosinuslar va sinuslar teoremalari
Lekin kosinuslar va sinuslar nafaqat to'g'ri burchakli uchburchaklarda ishlatilishi mumkin. O'tkir yoki o'tkir burchakning qiymatini, har qanday uchburchakning tomonini topish uchun kosinus va sinus teoremasini qo'llash kifoya.Kosinus teoremasi juda oddiy: "Uchburchakning bir tomonining kvadrati boshqa ikki tomonning kvadratlari yig'indisiga, bu tomonlarning ular orasidagi burchakning kosinusiga ikki baravar ko'paytmasiga teng".
Sinus teoremasining ikkita talqini mavjud: kichik va kengaytirilgan. Kichikga ko'ra: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir". Bu teorema ko'pincha uchburchak atrofida aylananing xossasi tufayli kengaytiriladi: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir va ularning nisbati aylananing diametriga tengdir".
Hosilalar
Hosila - bu argumentning o'zgarishiga nisbatan funktsiya qanchalik tez o'zgarishini ko'rsatadigan matematik vosita. Hosilalardan algebra, geometriya, iqtisod va fizika, bir qator texnik fanlarda foydalaniladi.Muammolarni hal qilishda siz trigonometrik funktsiyalar lotinlarining jadval qiymatlarini bilishingiz kerak: sinus va kosinus. Sinusning hosilasi kosinus, kosinusning hosilasi esa sinus, lekin minus belgisi bilan.
Matematikada qo'llash
Ayniqsa, ko'pincha to'g'ri burchakli uchburchaklar va ular bilan bog'liq masalalarni yechishda sinus va kosinuslardan foydalaniladi.Sinuslar va kosinuslarning qulayligi texnologiyada ham namoyon bo'ladi. Burchaklar va tomonlarni kosinus va sinus teoremalaridan foydalanib, murakkab shakllar va ob'ektlarni "oddiy" uchburchaklarga bo'lish orqali baholash oson edi. Ko'pincha tomonlar nisbati va daraja o'lchovlari bilan shug'ullanadigan muhandislar va arxitektorlar stol bo'lmagan burchaklarning kosinuslari va sinuslarini hisoblash uchun ko'p vaqt va kuch sarfladilar.
Keyin turli burchaklardagi sinuslar, kosinuslar, tangenslar va kotangenslarning minglab qiymatlarini o'z ichiga olgan Bradis jadvallari yordamga keldi. IN Sovet davri ba'zi o'qituvchilar o'z o'quvchilarini Bradys jadvallari sahifalarini yodlashga majbur qilishdi.
To'g'ri burchakli uchburchakda, eng oddiy ko'pburchaklar sifatida, turli mutaxassislar trigonometriya sohasidagi bilimlarini o'sha kunlarda hech kim matematikaning bu sohasini bu so'z bilan atamagan edi. Shu sababli, bu tekis geometrik shakldagi tomonlarning uzunliklari va burchaklar kattaliklarining nisbatlarida naqshlarni ochgan muallifni ko'rsatish bugungi kunda mumkin emas. Bunday munosabatlar trigonometrik funktsiyalar deb ataladi va bir nechta guruhlarga bo'linadi, ularning asosiylari shartli ravishda "to'g'ridan-to'g'ri" funktsiyalar hisoblanadi. Ushbu guruhga faqat ikkita funktsiya tayinlangan va ulardan biri sinusdir.
Ko'rsatma
Ta'rifga ko'ra, to'g'ri burchakli uchburchakda burchaklardan biri 90 ° ga teng va Evklid geometriyasidagi burchaklarining yig'indisi 180 ° ga teng bo'lishi kerakligi sababli, qolgan ikkita burchak o'tkirdir (ya'ni 90 ° dan kichik). ). Aynan shu burchaklar va yon uzunliklarning nisbatlarining qonuniyatlari trigonometrik funktsiyalarni tavsiflaydi.
O'tkir burchakning sinusi deb ataladigan funktsiya to'g'ri burchakli uchburchakning ikki tomonining uzunliklari orasidagi nisbatni aniqlaydi, ulardan biri bu o'tkir burchakka qarama-qarshi, ikkinchisi esa unga qo'shni va to'g'ri burchakka qarama-qarshi yotadi. Bunday uchburchakda to'g'ri burchakka qarama-qarshi tomon gipotenuza, qolgan ikkitasi esa oyoqlar deb ataladiganligi sababli, sinus funktsiyasining ta'rifini qarama-qarshi oyoq va gipotenuzaning uzunliklari orasidagi nisbat sifatida shakllantirish mumkin.
Ushbu trigonometrik funktsiyaning bunday sodda ta'rifiga qo'shimcha ravishda, bugungi kunda yanada murakkablari mavjud: Dekart koordinatalarida aylana orqali, ketma-ketlik orqali, differentsial va funktsional tenglamalar yechimlari orqali. Bu funksiya uzluksiz, ya’ni uning argumentlari (“ta’riflar sohasi”) har qanday son bo‘lishi mumkin – cheksiz salbiydan cheksiz ijobiygacha. Va bu funktsiyaning maksimal va minimal qiymatlari -1 dan +1 gacha bo'lgan oraliq bilan cheklangan - bu "uning qiymatlari diapazoni". Sinus o'zining minimal qiymatini 270 ° burchak ostida oladi, bu Pi ning 3/2 qismiga to'g'ri keladi va maksimal qiymat 90 ° (Pi ning ½) da olinadi. Funktsiya qiymatlari 0°, 180°, 360° va hokazolarda nolga aylanadi. Bularning barchasidan kelib chiqadiki, sinus davriy funktsiyadir va uning davri 360 ° ga yoki Pi sonining ikki barobariga teng.
Berilgan argument bo'yicha ushbu funktsiyaning qiymatlarini amaliy hisoblash uchun siz kalkulyatordan foydalanishingiz mumkin - ularning aksariyati (shu jumladan o'rnatilgan dasturiy kalkulyator). operatsion tizim kompyuteringiz) mos keladigan variantga ega.
Tegishli videolar
Ko'rsatma
burchak To'g'ri uchburchakda siz kosinus ta'rifidan foydalanishingiz va qo'shni oyoqning gipotenuzaga nisbatini topishingiz kerak:
chunki? = a/c, bu yerda a - oyoq uzunligi, c - gipotenuzaning uzunligi.
Agar siz kosinusni topishingiz kerak bo'lsa burchak ixtiyoriy uchburchakda kosinus teoremasidan foydalanish kerak:
burchak o'tkir bo'lsa: cos? = (a2 + b2 – c2)/(2ab);
burchak to'g'ridan-to'g'ri bo'lsa: cos? = (c2 - a2 - b2)/(2ab), bu erda a, b - burchakka ulashgan tomonlarning uzunligi, c - burchakka qarama-qarshi tomonning uzunligi.
Agar siz kosinusni topishingiz kerak bo'lsa burchak ixtiyoriy geometrik shaklda qiymatni aniqlash kerak burchak daraja yoki radianda va kosinusda burchak muhandislik kalkulyatori, Bradys jadvallari yoki boshqa matematik dastur yordamida uning kattaligi bo'yicha toping.
Kosinus burchakning asosiy trigonometrik funktsiyasidir. Kosinusni aniqlash qobiliyati vektor algebrasida vektorlarning turli o'qlardagi proyeksiyalarini aniqlashda foydalidir.
Ko'rsatma
cos?=(b?+c?-a?)/(2*b*c)
Tomonlari a, b, c mos ravishda 3, 4, 5 mm ga teng uchburchak mavjud.
Toping kosinus katta tomonlar orasiga o'ralgan burchak.
a orqali? tomoniga qarama-qarshi burchakni belgilaymiz, keyin yuqorida olingan formulaga ko'ra, bizda:
cos?=(b?+c?-a?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 =32/40=0,8
Javob: 0,8.
Agar uchburchak to'g'ri burchakli uchburchak bo'lsa, toping kosinus va burchakning istalgan ikki tomonining uzunligini bilish kifoya ( kosinus to'g'ri burchak 0).
Tomonlari a, b, c bo'lgan to'g'ri burchakli uchburchak bo'lsin, bu erda c - gipotenuza.
Barcha variantlarni ko'rib chiqing:
a va b tomonlarining uzunliklari ma'lum bo'lsa (uchburchakning oyoqlari) cosni toping.
Keling, qo'shimcha ravishda Pifagor teoremasidan foydalanamiz:
cos?=(b?+c?-a?)/(2*b*c)=(b?+b?+a?-a?)/(2*b*v(b?+a?)) =(2*b?)/(2*b*v(b?+a?))=b/v(b?+a?)
Olingan formulaning to'g'riligini tekshirish uchun biz 1-misoldagi qiymatlarni unga almashtiramiz, ya'ni.
Elementar hisob-kitoblarni amalga oshirib, biz quyidagilarni olamiz:
Xuddi shunday, bor kosinus to'rtburchak shaklida uchburchak boshqa hollarda:
Ma'lum a va c (gipotenuza va qarama-qarshi oyoq), cos toping?
cos?=(b?+c?-a?)/(2*b*c)=(c?-a?+c?-a?)/(2*c*v(c?-a?)) =(2*s?-2*a?)/(2*s*v(s?-a?))=v(s?-a?)/s.
Birinchi misoldagi a=3 va c=5 qiymatlarini almashtirsak, biz quyidagilarni olamiz:
b va c ma'lum (gipotenuza va qo'shni oyoq).
Sos topilsinmi?
Shunga o'xshash o'zgarishlarni amalga oshirgandan so'ng (2 va 3-misollarda ko'rsatilgan), bu holda biz buni olamiz kosinus V uchburchak juda oddiy formula yordamida hisoblab chiqiladi:
Olingan formulaning soddaligi elementar tarzda tushuntiriladi: aslida, burchakka ulashganmi? Oyoq gipotenuzaning proyeksiyasidir, shuning uchun uning uzunligi gipotenuzaning uzunligini cos? ga ko'paytirilganiga teng.
Birinchi misoldagi b = 4 va c = 5 qiymatlarini almashtirsak, biz quyidagilarni olamiz:
Shunday qilib, bizning barcha formulalarimiz to'g'ri.
Maslahat 5: To'g'ri burchakli uchburchakda o'tkir burchakni qanday topish mumkin
To'g'ridan-to'g'ri karbonli uchburchak, ehtimol, tarixiy nuqtai nazardan eng mashhurlaridan biri, geometrik shakllar. Pifagor "shimlari" faqat "Evrika!" Arximed.

Sizga kerak bo'ladi
- - uchburchakni chizish;
- - hukmdor;
- - transportyor.
Ko'rsatma
Uchburchak burchaklarining yig'indisi 180 daraja. to'rtburchak shaklida uchburchak bir burchak (o'ng) har doim 90 daraja bo'ladi, qolganlari esa o'tkir, ya'ni. har biri 90 darajadan kam. To'rtburchakda qaysi burchakni aniqlash uchburchak to'g'ri bo'lsa, uchburchakning tomonlarini chizg'ich bilan o'lchab, eng kattasini aniqlang. U gipotenuza (AB) deb ataladi va to'g'ri burchakka (C) qarama-qarshidir. Qolgan ikki tomon to'g'ri burchak hosil qiladi va oyoqlar (AC, BC) deb ataladi.
Qaysi burchak o'tkirligini aniqlaganingizdan so'ng, burchakni transportyor bilan o'lchashingiz yoki matematik formulalar yordamida hisoblashingiz mumkin.
O'tkazgich yordamida burchakning qiymatini aniqlash uchun uning ustki qismini (uni A harfi bilan belgilaymiz) o'tkazgich markazidagi chizg'ichga maxsus belgi bilan tekislang, AC oyog'i uning yuqori chetiga to'g'ri kelishi kerak. O'tkazgichning yarim doira shaklida gipotenuzasi AB o'tadigan nuqtani belgilang. Bu nuqtadagi qiymat gradusdagi burchak qiymatiga mos keladi. Agar o'tkazgichda 2 ta qiymat ko'rsatilgan bo'lsa, o'tkir burchak uchun siz kichikroqni, to'mtoq uchun - kattaroqni tanlashingiz kerak.
Bradis mos yozuvlar jadvallarida olingan qiymatni toping va olingan burchakka qaysi burchak mos kelishini aniqlang raqamli qiymat. Bizning buvilarimiz bu usuldan foydalanganlar.
Hozirgi vaqtda trigonometrik formulalarni hisoblash funktsiyasiga ega kalkulyatorni olish kifoya. Masalan, o'rnatilgan Windows kalkulyatori. "Kalkulyator" ilovasini ishga tushiring, "Ko'rish" menyusida "Muhandislik" bandini tanlang. Kerakli burchakning sinusini hisoblang, masalan, sin (A) = BC/AB = 2/4 = 0,5
Kalkulyator displeyidagi INV tugmasini bosish orqali kalkulyatorni teskari funktsiya rejimiga o'tkazing, so'ngra arksinus funktsiyasini hisoblash tugmachasini bosing (ekranda minus birinchi darajaga qadar gunoh sifatida belgilangan). Hisoblash oynasida quyidagi yozuv paydo bo'ladi: asind (0,5) = 30. Ya'ni, kerakli burchak 30 daraja.
Manbalar:
- Bradis jadvallari (sinuslar, kosinuslar)
Matematikada kosinus teoremasi ko'pincha uchinchi tomonni burchak va ikki tomon bilan topish kerak bo'lganda qo'llaniladi. Biroq, ba'zida muammoning sharti aksincha o'rnatiladi: berilgan uch tomon uchun burchakni topish talab qilinadi.

Ko'rsatma
Tasavvur qiling-a, sizga ikki tomonning uzunliklari va bir burchakning qiymati ma'lum bo'lgan uchburchak berilgan. Bu uchburchakning barcha burchaklari bir-biriga teng emas, tomonlari ham kattaligi jihatidan har xil. g burchak uchburchakning AB deb belgilangan tomoniga qarama-qarshi yotadi, bu rasmning asosi hisoblanadi. Ushbu burchak orqali, shuningdek, AC va BC qolgan tomonlari orqali siz kosinus teoremasidan foydalanib, uchburchakning noma'lum bo'lgan tomonini topishingiz mumkin, uning asosida quyidagi formula hosil bo'ladi:
a^2=b^2+c^2-2bc*cosy, bu yerda a=BC, b=AB, c=AC
Kosinus teoremasi boshqacha tarzda umumlashtirilgan Pifagor teoremasi deb ataladi.
O'qish foydali bo'lishi mumkin:
- Muqaddas mirra keltiruvchi ayollar kuni;
- Ehtirosli Yevgeniy Botkin shahid Yevgeniy Botkin;
- Muqaddas rap: Chuvashcha "Oxlobystin" o'smirlarga sevgi va kamtarlikni o'rgatadi.;
- Yeparxiya missionerlik kurslari: Protodeacon A ning missionerlik faoliyati haqida ma'ruza;
- Chayon nimani yoqtirishini qanday tushunish mumkin;
- Do'stlar bilan onlayn zombi apokalipsisi;
- Onlayn zombi apokalipsisi o'yinlari;
- FIFA o'yinini ishga tushirishda muammolar;