cos razmerje. Pravokotni trikotnik. Podrobna teorija s primeri
Navodilo
Metoda 1. Uporaba Pitagorejskega izreka. Izrek pravi: kvadrat hipotenuze je enak vsoti kvadratov katet. Iz tega sledi, da lahko katero koli stran pravokotnega trikotnika izračunamo ob poznavanju njegovih drugih dveh strani (slika 2)
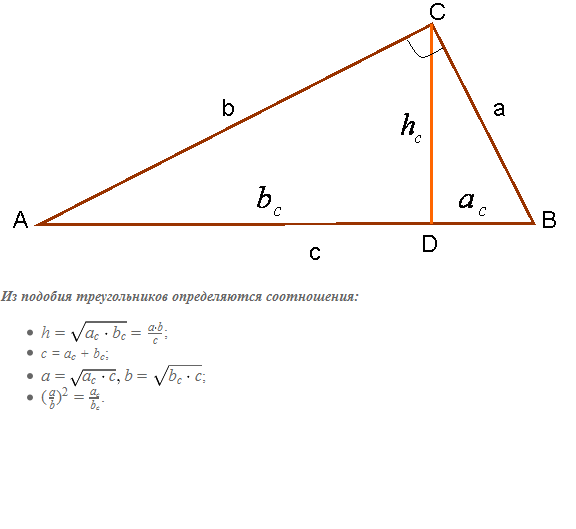
Metoda 2. Izhaja iz dejstva, da je mediana iz pravi kot na hipotenuzo, med seboj tvori 3 podobne trikotnike (slika 3). Na tej sliki so si trikotniki ABC, BCD in ACD podobni.
Hipotenuza je stranica v pravokotnem trikotniku, ki je nasproti kota 90 stopinj. Za izračun njegove dolžine je dovolj, da poznate dolžino ene od nog in vrednost enega od ostrih kotov trikotnika.

Navodilo
Z znano nogo in ostrim kotom pravokotnega trikotnika je lahko velikost hipotenuze enaka razmerju noge do kosinusa / sinusa tega kota, če je ta kot nasproti / sosednji:
h = C1(ali C2)/sinα;
h = С1(ali С2)/cosα.
Primer: Dan je pravokotni trikotnik ABC s hipotenuzo AB in pravim kotom C. Naj bo kot B 60 stopinj in kot A 30 stopinj. Dolžina kraka BC je 8 cm. Poiščite dolžino hipotenuze AB. Če želite to narediti, lahko uporabite katero koli od zgoraj predlaganih metod:
AB=BC/cos60=8 cm.
AB = BC/sin30 = 8 cm.
Hipotenuza je stranica pravokotnega trikotnika, ki je nasproti pravemu kotu. Je najdaljša stranica pravokotnega trikotnika. Izračunate ga lahko s pomočjo Pitagorovega izreka ali s pomočjo formul trigonometričnih funkcij.
![]()
Navodilo
Noge se imenujejo stranice pravokotnega trikotnika, ki mejijo na pravi kot. Na sliki sta kraka označena z AB in BC. Naj sta podani dolžini obeh krakov. Označimo jih z |AB| in |BC|. Da bi našli dolžino hipotenuze |AC|, uporabimo Pitagorov izrek. Po tem izreku je vsota kvadratov katet enaka kvadratu hipotenuze, tj. v zapisu naše risbe |AB|^2 + |BC|^2 = |AC|^2. Iz formule dobimo, da je dolžina hipotenuze AC določena kot |AC| = √(|AB|^2 + |BC|^2) .
Razmislite o primeru. Naj bosta dolžini krakov |AB| = 13, |BC| = 21. Po Pitagorovem izreku dobimo, da je |AC|^2 = 13^2 + 21^2 = 169 + 441 = 610. iz številke 610: |AC| = √610. S pomočjo tabele kvadratov celih števil ugotovimo, da število 610 ni popoln kvadrat nobenega celega števila. Da bi dobili končno vrednost dolžine hipotenuze, poskusimo izpod znaka korena vzeti polni kvadrat. Da bi to naredili, razčlenimo število 610 na faktorje. 610 = 2 * 5 * 61. Glede na tabelo praštevila Vidimo, da je 61 praštevilo. Zato je nadaljnje zmanjševanje števila √610 nemogoče. Dobimo končni odgovor |AC| = √610.
Če bi bil kvadrat hipotenuze na primer 675, potem je √675 = √(3 * 25 * 9) = 5 * 3 * √3 = 15 * √3. Če je takšen odlitek mogoč, izvedite obratno preverjanje - rezultat kvadrirajte in primerjajte z izvirno vrednostjo.
Spoznajmo enega od krakov in nanj priležni kot. Za določnost naj bo to krak |AB| in kot α. Nato lahko uporabimo formulo za kosinus trigonometrične funkcije - kosinus kota je enak razmerju sosednjega kraka proti hipotenuzi. Tisti. v našem zapisu cos α = |AB| / |AC|. Od tu dobimo dolžino hipotenuze |AC| = |AB| / cosα.
Če poznamo krak |BC| in kota α, potem uporabimo formulo za izračun sinusa kota - sinus kota je enak razmerju nasprotnega kraka proti hipotenuzi: sin α = |BC| / |AC|. Dobimo, da je dolžina hipotenuze najdena kot |AC| = |BC| / cosα.
Za jasnost upoštevajte primer. Naj bo dolžina kraka |AB| = 15. In kot α = 60°. Dobimo |AC| = 15 / cos 60° = 15 / 0,5 = 30.
Razmislite, kako lahko preverite svoj rezultat z uporabo Pitagorovega izreka. Za to moramo izračunati dolžino drugega kraka |BC|. Z uporabo formule za tangens kota tg α = |BC| / |AC|, dobimo |BC| = |AB| * tg α = 15 * tg 60° = 15 * √3. Nato uporabimo Pitagorov izrek in dobimo 15^2 + (15 * √3)^2 = 30^2 => 225 + 675 = 900. Preverjanje je opravljeno.
Po izračunu hipotenuze preverite, ali dobljena vrednost ustreza Pitagorovemu izreku.
Viri:
- Tabela praštevil od 1 do 10000
Noge poimenujte dve kratki strani pravokotnega trikotnika, ki sestavljata njegovo oglišče, katerega vrednost je 90 °. Tretja stran v takem trikotniku se imenuje hipotenuza. Vse te strani in koti trikotnika so med seboj povezani z določenimi razmerji, ki vam omogočajo izračun dolžine noge, če je znanih več drugih parametrov.

Navodilo
Za izračun dolžine kraka (A) uporabite Pitagorov izrek, če poznate dolžino drugih dveh strani (B in C) pravokotnega trikotnika. Ta izrek pravi, da je vsota kvadratov dolžin katet enaka kvadratu hipotenuze. Iz tega sledi, da je dolžina vsakega od krakov enaka kvadratnemu korenu razlike med kvadrati dolžin hipotenuze in drugega kraka: A=√(C²-B²).
Uporabite definicijo neposredne trigonometrične funkcije "sinus" za ostri kot, če poznate vrednost kota (α) nasproti izračunanega kraka in dolžino hipotenuze (C). Ta definicija navaja, da je sinus tega znani kot enaka razmerju med dolžino želenega kraka in dolžino hipotenuze. To pomeni, da je dolžina želenega kraka enaka produktu dolžine hipotenuze in sinusa znanega kota: A=C∗sin(α). Za iste znane vrednosti lahko uporabite definicijo funkcije kosekansa in izračunate želeno dolžino tako, da dolžino hipotenuze delite s kosekansom znanega kota A=C/cosec(α).
Uporabite definicijo kosinusa direktne trigonometrične funkcije, če je poleg dolžine hipotenuze (C) znana tudi vrednost ostrega kota (β), ki meji na želeni krak. Kosinus tega kota je definiran kot razmerje dolžin želenega kraka in hipotenuze, iz tega pa lahko sklepamo, da je dolžina kraka enaka produktu dolžine hipotenuze in kosinusa znanega kot: A=C∗cos(β). Uporabite lahko definicijo funkcije sekante in izračunate želeno vrednost tako, da dolžino hipotenuze delite s sekansom znanega kota A=C/sec(β).
Izpelji zahtevano formulo iz podobne definicije za odvod trigonometrične funkcije tangenta, če je poleg vrednosti ostrega kota (α), ki leži nasproti želenega kraka (A), dolžina drugega kraka (B) enaka znan. Tangens kota nasproti želenega kraka je razmerje med dolžino tega kraka in dolžino drugega kraka. To pomeni, da bo želena vrednost enaka produktu dolžine znanega kraka in tangensa znanega kota: A=B∗tg(α). Iz teh istih znanih količin je mogoče izpeljati drugo formulo z uporabo definicije kotangensne funkcije. V tem primeru bo za izračun dolžine kraka potrebno najti razmerje med dolžino znanega kraka in kotangensom znanega kota: A=B/ctg(α).
Sorodni videoposnetki
Beseda "katet" je prišla v ruščino iz grščine. V natančnem prevodu pomeni navpična črta, to je pravokotno na površino zemlje. V matematiki se noge imenujejo stranice, ki tvorijo pravi kot pravokotnega trikotnika. Stran nasproti tega kota se imenuje hipotenuza. Izraz "noga" se uporablja tudi v arhitekturi in varilni tehnologiji.

Nariši pravokotni trikotnik ACB. Označi njegovi kateti a in b ter hipotenuzo c. Vse stranice in koti pravokotnega trikotnika so povezani z določenimi relacijami. Razmerje noge nasproti enega od ostrih kotov do hipotenuze se imenuje sinus tega kota. V tem trikotniku sinCAB=a/c. Kosinus je razmerje s hipotenuzo sosednjega kraka, tj. cosCAB=b/c. Inverzna razmerja imenujemo sekans in kosekans.
Sekans tega kota dobimo tako, da hipotenuzo delimo s sosednjim krakom, to je secCAB=c/b. Izkaže se recipročna vrednost kosinusa, to je, da jo lahko izrazimo s formulo secCAB=1/cosSAB.
Kosekans je enak količniku deljenja hipotenuze z nasprotnim krakom in je recipročna vrednost sinusa. Izračuna se lahko z uporabo formule cosecCAB=1/sinCAB
Oba kraka sta povezana s tangento in kotangensom. IN ta primer tangenta bo razmerje med stranjo a in stranjo b, to je nasprotni krak do sosednjega. To razmerje lahko izrazimo s formulo tgCAB=a/b. V skladu s tem bo obratno razmerje kotangens: ctgCAB=b/a.
Razmerje med velikostjo hipotenuze in obeh katet je določil starogrški matematik Pitagora. Izrek, poimenovan po njem, ljudje še vedno uporabljajo. Pravi, da je kvadrat hipotenuze enak vsoti kvadratov nog, to je c2 \u003d a2 + b2. V skladu s tem bo vsak krak enak kvadratnemu korenu razlike med kvadratoma hipotenuze in drugega kraka. To formulo lahko zapišemo kot b=√(c2-a2).
Dolžino kraka lahko izrazite tudi z razmerji, ki jih poznate. Po izrekih sinusov in kosinusov je noga enaka zmnožku hipotenuze in ene od teh funkcij. Lahko se izrazi tudi s tangensom ali kotangensom. Nogo a lahko najdete na primer s formulo a \u003d b * tan CAB. Na popolnoma enak način, odvisno od danega tangensa ali kotangensa, se določi drugi krak.
V arhitekturi se uporablja tudi izraz "noga". Uporablja se za jonski kapitel in označuje navpično črto skozi sredino njegovega hrbta. To pomeni, da v tem primeru ta izraz označuje pravokotno na dano črto.
V varilni tehnologiji obstaja pojem "kotni zvar". Kot v drugih primerih je to najkrajša razdalja. Tukaj pogovarjamo se o vrzeli med enim od delov, ki jih je treba zvariti, do roba šiva, ki se nahaja na površini drugega dela.
Sorodni videoposnetki
Viri:
- kaj sta kateta in hipotenuza
Sorodni videoposnetki
Opomba
Pri izračunu strani pravokotnega trikotnika se lahko igra poznavanje njegovih značilnosti:
1) Če krak pravega kota leži nasproti kota 30 stopinj, potem je enak polovici hipotenuze;
2) Hipotenuza je vedno daljša od katere koli noge;
3) Če je okrog pravokotnega trikotnika opisan krog, mora njegovo središče ležati na sredini hipotenuze.
Trigonometrija je veja matematike, ki proučuje trigonometrične funkcije in njihovo uporabo v praksi. Te funkcije vključujejo sinusov, kosinus, tangens in kotangens.
Sinus je trigonometrična funkcija , razmerje med velikostjo nasprotnega kraka in velikostjo hipotenuze.
Sinus v trigonometriji.
Kot je navedeno zgoraj, je sinus neposredno povezan s trigonometrijo in trigonometričnimi funkcijami. Njegovo funkcijo določa
- pomoč pri izračunu kota, če so znane mere stranic trikotnika;
- pomoč pri izračunu velikosti stranice trikotnika, če je znan kot.
Ne smemo pozabiti, da bo vrednost sinusa vedno enaka za katero koli velikost trikotnika, saj sinus ni meritev, ampak razmerje.
Posledično, da ne bi izračunali te konstantne vrednosti za vsako rešitev določenega problema, so bile ustvarjene posebne trigonometrične tabele. V njih so vrednosti sinusov, kosinusov, tangentov in kotangensov že izračunane in določene. Običajno so te tabele podane na vzvratnem listu učbenikov o algebri in geometriji. Najdemo jih tudi na internetu.
Sinus v geometriji.
Geometrija torej zahteva vizualizacijo, da bi razumeli v praksi, kaj je sinus kota, morate narisati trikotnik s pravim kotom.
Predpostavimo, da so stranice, ki tvorijo pravi kot, poimenovane a, c, nasprotni kot X.
Običajno je dolžina stranic navedena v nalogah. Recimo a=3, b=4. V tem primeru bo razmerje stranic videti kot ¾. Poleg tega, če podaljšamo stranice trikotnika, ki mejijo na ostri kot X, potem se bodo strani povečale A in V, hipotenuza pa je tretja stranica pravokotnega trikotnika, ki ni pravokotna na osnovo. Zdaj lahko stranice trikotnika imenujemo drugače, na primer: m, n, k.
S to spremembo je zakon trigonometrije deloval: dolžine stranic trikotnika so se spremenile, njihovo razmerje pa ne.
Dejstvo, da če spremenite dolžine strani trikotnika tolikokrat, kot želite, in pri tem ohranite vrednost kota x, bo razmerje med njegovimi stranicami še vedno ostalo nespremenjeno, so opazili starodavni znanstveniki. V našem primeru bi se lahko dolžine strani spreminjale takole: a / b \u003d ¾, ko je stranica podaljšana A do 6 cm in V- do 8 cm dobimo: m/n = 6/8 = 3/4.
Razmerje stranic v pravokotnem trikotniku se v zvezi s tem imenuje:
- sinus kota x je razmerje med nasprotnim krakom in hipotenuzo: sinx = a/c;
- kosinus kota x je razmerje med sosednjim krakom in hipotenuzo: cosx = w/s;
- tangens kota x je razmerje med nasprotno nogo in sosednjo: tgx \u003d a / b;
- kotangens kota x je razmerje med sosednjim krakom in nasprotnim: ctgx \u003d in / a.
Preučevanje trigonometrije začnemo s pravokotnim trikotnikom. Določimo, kaj sta sinus in kosinus, pa tudi tangens in kotangens ostrega kota. To so osnove trigonometrije.
Spomni se tega pravi kot je kot enak . Z drugimi besedami, polovica razgrnjenega kota.
Oster kot- manjši.
Topi kot- večji. V zvezi s takim kotom "top" ni žaljivka, ampak matematični izraz :-)

Narišimo pravokotni trikotnik. Običajno je označen pravi kot. Upoštevajte, da je stran nasproti vogala označena z isto črko, le majhna. Torej je označena stran, ki leži nasproti kota.
Kot je označen z ustrezno grško črko.
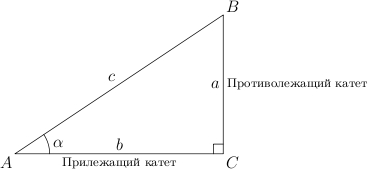
hipotenuza Pravokotni trikotnik je stran nasproti pravega kota.
Noge- strani nasproti ostrih vogalov.
Noga nasproti vogala se imenuje nasprotje(glede na kot). Druga noga, ki leži na eni strani vogala, se imenuje sosednji.
Sinus ostri kot v pravokotnem trikotniku je razmerje med nasprotnim krakom in hipotenuzo:
Kosinus ostri kot v pravokotnem trikotniku - razmerje med sosednjo nogo in hipotenuzo:
Tangenta ostri kot v pravokotnem trikotniku - razmerje med nasprotno nogo in sosednjo:
Druga (enakovredna) definicija: tangens ostrega kota je razmerje med sinusom kota in njegovim kosinusom:
![]()
Kotangens ostri kot v pravokotnem trikotniku - razmerje med sosednjo nogo in nasprotno (ali enako razmerje med kosinusom in sinusom):
![]()
Bodite pozorni na osnovna razmerja za sinus, kosinus, tangens in kotangens, ki so navedena spodaj. Koristili nam bodo pri reševanju težav.
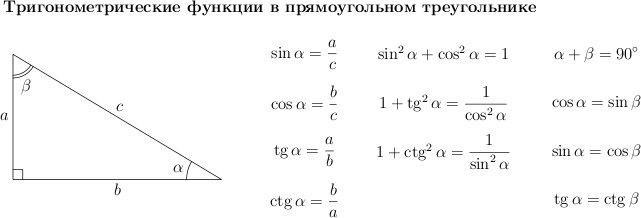
Dokažimo nekatere izmed njih.
1. Vsota kotov katerega koli trikotnika je . pomeni, vsota dveh ostrih kotov pravokotnega trikotnika je .
2. Na eni strani kot razmerje med nasprotno nogo in hipotenuzo. Po drugi strani pa, ker bo za kot noga sosednja.
To razumemo ![]() . Z drugimi besedami, .
. Z drugimi besedami, .
3. Vzemite Pitagorov izrek: ![]() . Oba dela razdelimo na:
. Oba dela razdelimo na:
![]()
Imamo osnovna trigonometrična identiteta:
Tako lahko, če poznamo sinus kota, najdemo njegov kosinus in obratno.
4. Če oba dela glavne trigonometrične identitete delimo z , dobimo:
![]()
To pomeni, da če nam je dan tangens ostrega kota, potem lahko takoj najdemo njegov kosinus.
prav tako
![]()
V redu, dali smo definicije in zapisali formule. Toda zakaj potrebujemo sinus, kosinus, tangens in kotangens?
To vemo vsota kotov katerega koli trikotnika je.
Poznamo razmerje med stranke pravokotni trikotnik. To je Pitagorov izrek: ![]() .
.
Izkazalo se je, da če poznate dva kota v trikotniku, lahko najdete tretjega. Če poznate dve strani pravokotnega trikotnika, lahko najdete tretjo. Torej, za kote - njihovo razmerje, za stranice - svoje. Toda kaj storiti, če sta v pravokotnem trikotniku znani en kot (razen pravega) in ena stran, vendar morate najti druge strani?
Sprva sta sinus in kosinus nastala zaradi potrebe po izračunavanju količin v pravokotnih trikotnikih. Ugotovljeno je bilo, da če se vrednost stopinjske mere kotov v pravokotnem trikotniku ne spremeni, potem razmerje stranic, ne glede na to, koliko se te strani spremenijo v dolžino, vedno ostane enako.Tako sta bila uvedena pojma sinus in kosinus. Sinus ostrega kota v pravokotnem trikotniku je razmerje med nasprotnim krakom in hipotenuzo, kosinus pa je razmerje med sosednjim krakom in hipotenuzo.
Izreki kosinusov in sinusov
Toda kosinuse in sinuse je mogoče uporabiti ne samo v pravokotnih trikotnikih. Če želite najti vrednost tupega ali ostrega kota, strani katerega koli trikotnika, je dovolj uporabiti kosinusni in sinusni izrek.Kosinusni izrek je povsem preprost: "Kvadrat strani trikotnika je enak vsoti kvadratov drugih dveh strani minus dvakratni produkt teh stranic s kosinusom kota med njima."
Obstajata dve razlagi sinusnega izreka: majhna in razširjena. Po malem: "V trikotniku so koti sorazmerni z nasprotnimi stranicami." Ta izrek se pogosto razširi zaradi lastnosti kroga, opisanega okoli trikotnika: "V trikotniku so koti sorazmerni z nasprotnimi stranicami, njuno razmerje pa je enako premeru okoli njega opisanega kroga."
Odvod
Izpeljanka je matematično orodje, ki pokaže, kako hitro se funkcija spremeni glede na spremembo njenega argumenta. Izpeljanke se uporabljajo v algebri, geometriji, ekonomiji in fiziki ter številnih tehničnih disciplinah.Pri reševanju problemov morate poznati tabelarične vrednosti derivatov trigonometričnih funkcij: sinusa in kosinusa. Odvod sinusa je kosinus, odvod kosinusa pa sinus, vendar z znakom minus.
Uporaba v matematiki
Še posebej pogosto se sinusi in kosinusi uporabljajo pri reševanju pravokotnih trikotnikov in z njimi povezanih problemov.Priročnost sinusov in kosinusov se odraža tudi v tehnologiji. Kote in stranice je bilo enostavno ovrednotiti z uporabo kosinusnega in sinusnega izreka, pri čemer so kompleksne oblike in predmete razdelili na "preproste" trikotnike. Inženirji in arhitekti, ki se pogosto ukvarjajo z izračuni razmerij stranic in stopinjskih mer, so porabili veliko časa in truda za izračun kosinusov in sinusov netabelnih kotov.
Nato so na pomoč priskočile Bradisove tabele, ki vsebujejo na tisoče vrednosti sinusov, kosinusov, tangentov in kotangensov različnih kotov. IN Sovjetski čas nekateri učitelji so prisilili svoje učence, da so si zapomnili strani Bradyjevih tabel.
Na pravokotnem trikotniku, kot najpreprostejšem mnogokotniku, so različni poznavalci izpopolnjevali svoje znanje na področju trigonometrije že v tistih časih, ko tega področja matematike še nihče ni imenoval s to besedo. Zato danes ni mogoče navesti avtorja, ki je razkril vzorce v razmerjih dolžin stranic in velikosti kotov v tem ploščatem geometrijskem liku. Takšni odnosi se imenujejo trigonometrične funkcije in so razdeljeni v več skupin, od katerih se glavne običajno štejejo za "neposredne" funkcije. Tej skupini sta dodeljeni le dve funkciji in ena od njih je sinusna.
Navodilo
Po definiciji je v pravokotnem trikotniku eden od kotov enak 90°, in ker mora biti vsota njegovih kotov v evklidski geometriji enaka 180°, sta druga dva kota ostra (tj. manjša od 90°). ). Pravilnosti razmerij natanko teh kotov in dolžin stranic opisujejo trigonometrične funkcije.
Funkcija, imenovana sinus ostrega kota, določa razmerje med dolžinama dveh stranic pravokotnega trikotnika, od katerih ena leži nasproti tega ostrega kota, druga pa je z njim sosednja in leži nasproti pravega kota. Ker se stran nasproti pravega kota v takem trikotniku imenuje hipotenuza, drugi dve pa sta kraka, lahko definicijo sinusne funkcije formuliramo kot razmerje med dolžinami nasprotnega kraka in hipotenuze.
Poleg tako enostavne definicije te trigonometrične funkcije danes obstajajo bolj zapletene: skozi krožnico v kartezičnih koordinatah, preko nizov, preko rešitev diferencialnih in funkcionalnih enačb. Ta funkcija je zvezna, kar pomeni, da so njeni argumenti ("domena definicij") lahko poljubno število - od neskončno negativnih do neskončno pozitivnih. Največje in najmanjše vrednosti te funkcije so omejene z razponom od -1 do +1 - to je "razpon njenih vrednosti". Sinus ima najmanjšo vrednost pri kotu 270°, kar ustreza 3/2 Pi, največjo vrednost pa dobimo pri 90° (½ Pi). Vrednosti funkcije postanejo nič pri 0°, 180°, 360° itd. Iz vsega tega sledi, da je sinus periodična funkcija in je njegova doba enaka 360 ° ali dvakratnemu številu Pi.
Za praktične izračune vrednosti te funkcije iz danega argumenta lahko uporabite kalkulator – veliko večino (vključno s programskim kalkulatorjem, vgrajenim v operacijski sistem vaš računalnik) ima ustrezno možnost.
Sorodni videoposnetki
Navodilo
kota v pravokotnem trikotniku morate uporabiti definicijo kosinusa in poiskati razmerje med sosednjo nogo in hipotenuzo:
cos? = a/c, kjer je a dolžina katete, c je dolžina hipotenuze.
Če morate najti kosinus kota v poljubnem trikotniku je treba uporabiti kosinusni izrek:
če je kot oster: cos? = (a2 + b2 – c2)/(2ab);
če je kot top: cos? = (c2 - a2 - b2)/(2ab), kjer sta a, b dolžini stranic, ki mejijo na kot, c je dolžina stranice nasproti kotu.
Če morate najti kosinus kota v poljubnem geometrijskem liku je treba določiti vrednost kota v stopinjah ali radianih in kosinus kota poiščite po njegovi velikosti z uporabo inženirskega kalkulatorja, tabel Bradys ali katere koli druge matematične aplikacije.
Kosinus je osnovna trigonometrična funkcija kota. Sposobnost določanja kosinusa je uporabna v vektorski algebri pri določanju projekcij vektorjev na različne osi.
Navodilo
cos?=(b?+c?-a?)/(2*b*c)
Obstaja trikotnik s stranicami a, b, c enakimi 3, 4, 5 mm.
Najti kosinus kot, sklenjen med velikimi stranicami.
Označimo kot, ki je nasproti strani a skozi?, potem imamo po zgornji formuli:
cos?=(b?+c?-a?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40 =32/40=0,8
Odgovor: 0,8.
Če je trikotnik pravokoten trikotnik, potem najti kosinus in dovolj je poznati dolžini poljubnih dveh stranic kota ( kosinus pravi kot je 0).
Naj obstaja pravokotni trikotnik s stranicami a, b, c, kjer je c hipotenuza.
Upoštevajte vse možnosti:
Poiščite cos?, če sta znani dolžini strani a in b (kraka trikotnika)
Uporabimo še Pitagorov izrek:
cos?=(b?+c?-a?)/(2*b*c)=(b?+b?+a?-a?)/(2*b*v(b?+a?)) =(2*b?)/(2*b*v(b?+a?))=b/v(b?+a?)
Da preverimo pravilnost dobljene formule, vanjo nadomestimo vrednosti iz primera 1, tj.
Po osnovnih izračunih dobimo:
Podobno obstaja kosinus v pravokotniku trikotnik v drugih primerih:
Znana a in c (hipotenuza in nasprotni krak), poiščite cos?
cos?=(b?+c?-a?)/(2*b*c)=(c?-a?+c?-a?)/(2*c*v(c?-a?)) =(2*s?-2*a?)/(2*s*v(s?-a?))=v(s?-a?)/s.
Če nadomestimo vrednosti a=3 in c=5 iz prvega primera, dobimo:
b in c sta znana (hipotenuza in sosednji krak).
Najdi cos?
Ko smo izvedli podobne transformacije (prikazane v primerih 2 in 3), dobimo v tem primeru to kosinus V trikotnik izračunano po zelo preprosti formuli:
Enostavnost izpeljane formule je razložena na elementaren način: v resnici meji na vogalu? Krak je projekcija hipotenuze, zato je njegova dolžina enaka dolžini hipotenuze, pomnoženi s cos?.
Če nadomestimo vrednosti b=4 in c=5 iz prvega primera, dobimo:
Torej so vse naše formule pravilne.
Nasvet 5: Kako najti oster kot v pravokotnem trikotniku
Neposredno karbonski trikotnik je z zgodovinskega vidika verjetno eden najbolj znanih, geometrijske oblike. Pitagorejske "hlače" se lahko kosajo le z "Eureko!" Arhimed.

Boste potrebovali
- - risanje trikotnika;
- - ravnilo;
- - kotomer.
Navodilo
Vsota kotov trikotnika je 180 stopinj. v pravokotniku trikotnik en kot (desni) bo vedno 90 stopinj, ostali pa so ostri, tj. manj kot 90 stopinj vsak. Da bi ugotovili, kateri kot v pravokotniku trikotnik je ravna, z ravnilom izmerite stranice trikotnika in določite največjo. Imenuje se hipotenuza (AB) in je nasproti pravemu kotu (C). Preostali dve stranici tvorita pravi kot in se imenujeta kraka (AC, BC).
Ko ugotovite, kateri kot je oster, lahko kot izmerite s kotomerjem ali pa ga izračunate z matematičnimi formulami.
Če želite določiti vrednost kota s kotomerjem, poravnajte njegov vrh (označimo ga s črko A) s posebno oznako na ravnilu v sredini kotomerja, AC noga mora sovpadati z njegovim zgornjim robom. Na polkrožnem delu kotomera označimo točko, skozi katero poteka hipotenuza AB. Vrednost na tej točki ustreza vrednosti kota v stopinjah. Če sta na kotomerju navedeni 2 vrednosti, potem morate za oster kot izbrati manjši, za tupi - večji.
Poiščite nastalo vrednost v referenčnih tabelah Bradis in določite, kateri kot ustreza prejetemu številčna vrednost. To metodo so uporabljale naše babice.
Dandanes je dovolj, da vzamete kalkulator s funkcijo izračunavanja trigonometričnih formul. Na primer vgrajeni kalkulator Windows. Zaženite aplikacijo "Kalkulator", v meniju "Pogled" izberite postavko "Inženiring". Izračunajte sinus želenega kota, na primer sin (A) = BC/AB = 2/4 = 0,5
Kalkulator preklopite v način inverzne funkcije s klikom na gumb INV na zaslonu kalkulatorja, nato kliknite gumb za izračun funkcije arkusina (na zaslonu je označen kot sin na minus prvo stopnjo). V oknu za izračun se bo pojavil naslednji napis: asind (0,5) = 30. To je, želeni kot je 30 stopinj.
Viri:
- Bradisove tabele (sinusov, kosinusov)
Kosinusni izrek v matematiki se najpogosteje uporablja, ko je treba najti tretjo stran s kotom in dvema stranema. Vendar pa je včasih pogoj problema zastavljen obratno: treba je najti kot za dane tri stranice.

Navodilo
Predstavljajte si, da imate trikotnik z znanimi dolžinami obeh stranic in vrednostjo enega kota. Vsi koti tega trikotnika niso enaki med seboj, njegove stranice pa so tudi različno velike. Kot γ leži nasproti stranice trikotnika, označenega z AB, ki je osnova tega lika. Skozi ta kot, kot tudi skozi preostale stranice AC in BC, lahko najdete stran trikotnika, ki je neznana, z uporabo kosinusnega izreka in na njegovi podlagi izpeljete spodnjo formulo:
a^2=b^2+c^2-2bc*cosγ, kjer je a=BC, b=AB, c=AC
Kosinusni izrek sicer imenujemo posplošen Pitagorov izrek.
Morda bi bilo koristno prebrati:
- Dan svetih žena, ki nosijo miro;
- Pasijonosec Jevgenij Botkin Mučenik Jevgenij Botkin;
- Sveti rap: Čuvaški "Okhlobystin" z recitativom uči najstnike ljubezni in ponižnosti;
- Škofijski misijonski tečaji: Predavanje o misijonskem delu protodiakona A;
- Kako razumeti, kaj je všeč škorpijonu;
- Zombi apokalipsa na spletu s prijatelji;
- Igre na spletu igranje zombi apokalipse;
- Težave pri zagonu igre Fifa;